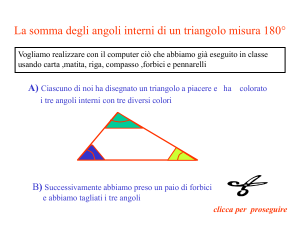
ALCUNE PROPRIETÀ DEGLI ANGOLI
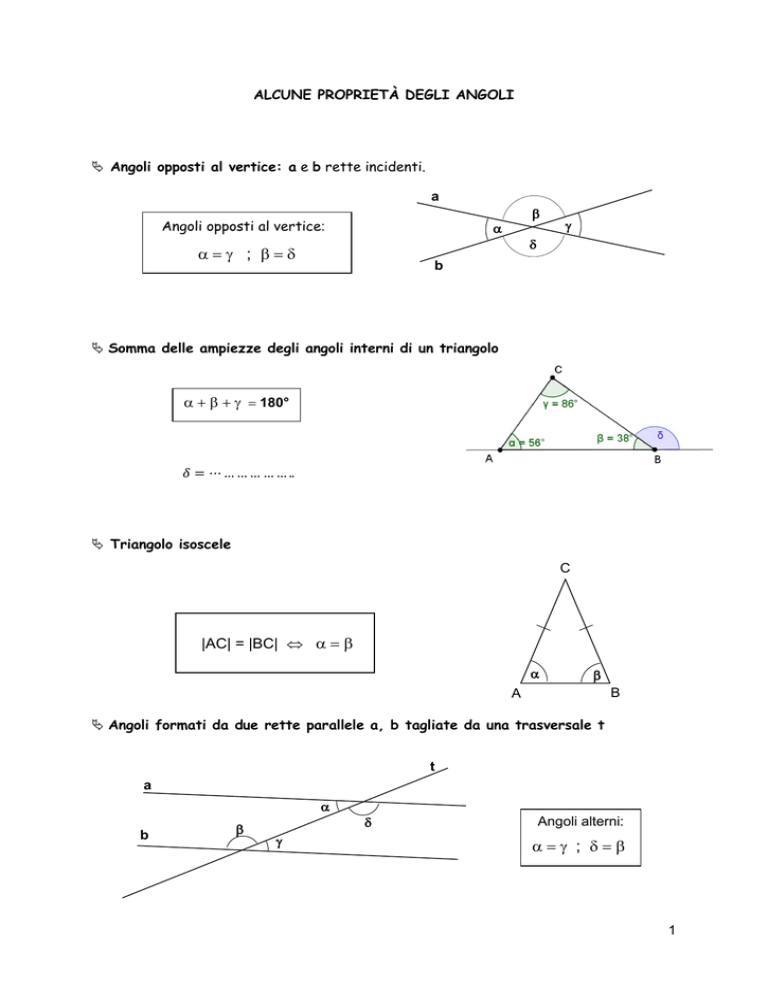
Angoli opposti al vertice: a e b rette incidenti.
a
Angoli opposti al vertice:
;
b
Somma delle ampiezze degli angoli interni di un triangolo
180°
𝛿 = ⋯ … … … … … ..
Triangolo isoscele
C
|AC| = |BC|
B
A
Angoli formati da due rette parallele a, b tagliate da una trasversale t
t
a
b
Angoli alterni:
;
1
ESERCIZI SUGLI ANGOLI
Nelle seguenti figure:
- il simbolo // indica che le rette così contrassegnate sono parallele;
- il simbolo o indica il centro di un arco di circonferenza disegnato.
Determina le ampiezze indicate dalle lettere greche, spiegando, su un foglio a
parte, i passaggi che ti conducono alla soluzione.
1.
d
2.
d
327°
127°
4.
d
3.
d
110°
4
5.
d
6.
d
44°
95°
28°
8.
d
7.
d
79°
55°
115°
2
9.
d
10.
d
82°
142°
11.
18°
82°
13.
12.
54°
126°
108°
14.
40°
15.
30°
70°
3
Applicazioni alla similitudine.
Nelle seguenti figure, ricercare la similitudine dei triangoli, specificando la congruenza
degli angoli.
Figura 2
Figura 1
Figura 3
Figura 4
Figura 6
Figura 5
Esercizi:
a) Rappresenta un triangolo ABC.
Rappresenta il triangolo A’B’C’ avente per vertici i punti medi del primo triangolo.
Osserva le due figure geometriche: puoi dire che sono simili? Perché?
b) Rappresenta un poligono non regolare.
Rappresenta il poligono avente per vertici i punti medi del primo poligono.
Osserva le due figure geometriche: puoi dire che sono simili?
4