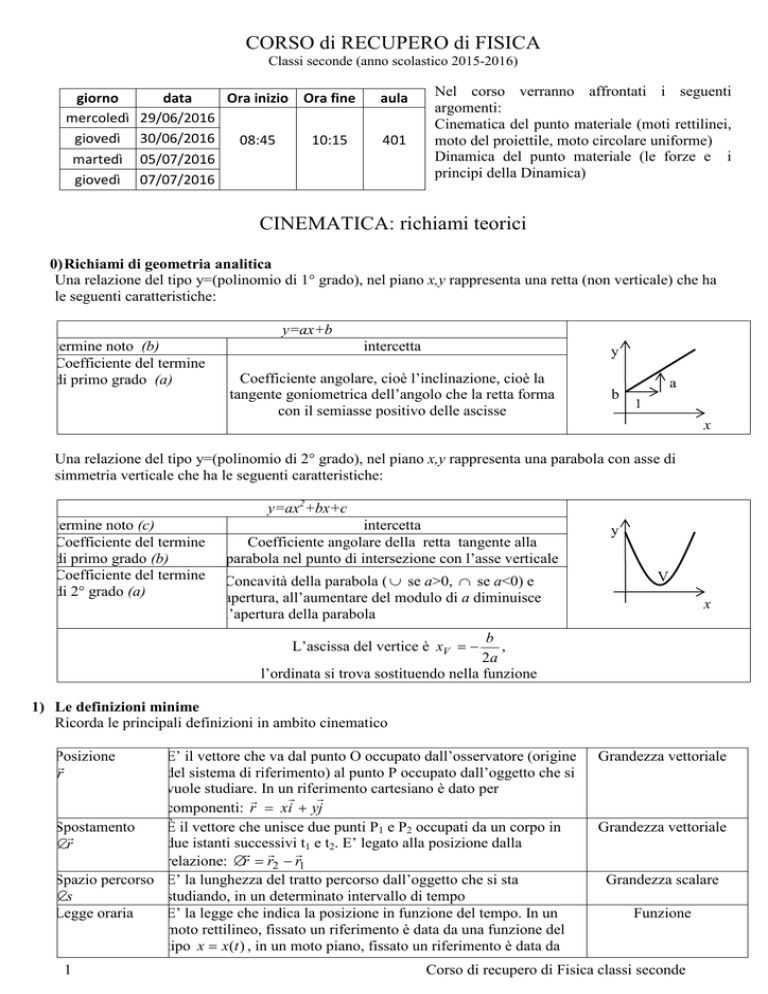
CORSO di RECUPERO di FISICA
Classi seconde (anno scolastico 2015-2016)
giorno
mercoledì
giovedì
martedì
giovedì
data
Ora inizio Ora fine
29/06/2016
30/06/2016
08:45
10:15
05/07/2016
07/07/2016
aula
401
Nel corso verranno affrontati i seguenti
argomenti:
Cinematica del punto materiale (moti rettilinei,
moto del proiettile, moto circolare uniforme)
Dinamica del punto materiale (le forze e i
principi della Dinamica)
CINEMATICA: richiami teorici
0) Richiami di geometria analitica
Una relazione del tipo y=(polinomio di 1° grado), nel piano x,y rappresenta una retta (non verticale) che ha
le seguenti caratteristiche:
y=ax+b
termine noto (b)
Coefficiente del termine
di primo grado (a)
intercetta
y
Coefficiente angolare, cioè l’inclinazione, cioè la
tangente goniometrica dell’angolo che la retta forma
con il semiasse positivo delle ascisse
b
a
1
x
Una relazione del tipo y=(polinomio di 2° grado), nel piano x,y rappresenta una parabola con asse di
simmetria verticale che ha le seguenti caratteristiche:
y=ax2+bx+c
termine noto (c)
Coefficiente del termine
di primo grado (b)
Coefficiente del termine
di 2° grado (a)
intercetta
Coefficiente angolare della retta tangente alla
parabola nel punto di intersezione con l’asse verticale
Concavità della parabola ( ∪ se a>0, ∩ se a<0) e
apertura, all’aumentare del modulo di a diminuisce
l’apertura della parabola
y
V
x
b
,
2a
l’ordinata si trova sostituendo nella funzione
L’ascissa del vertice è xV = −
1) Le definizioni minime
Ricorda le principali definizioni in ambito cinematico
Posizione
r
r
E’ il vettore che va dal punto O occupato dall’osservatore (origine
del sistema di riferimento) al punto P occupato dall’oggetto che si
vuole studiare. In un riferimento cartesiano è dato per
r r
r
componenti: r = xi + yj
Spostamento
È il vettore che unisce due punti P1 e P2 occupati da un corpo in
r
due istanti successivi t1 e t2. E’ legato alla posizione dalla
∆r
r r r
relazione: ∆r = r2 − r1
Spazio percorso E’ la lunghezza del tratto percorso dall’oggetto che si sta
studiando, in un determinato intervallo di tempo
∆s
Legge oraria
E’ la legge che indica la posizione in funzione del tempo. In un
moto rettilineo, fissato un riferimento è data da una funzione del
tipo x = x(t ) , in un moto piano, fissato un riferimento è data da
1
Grandezza vettoriale
Grandezza vettoriale
Grandezza scalare
Funzione
Corso di recupero di Fisica classi seconde
r
r r
r = f (t ) oppure r = r (t )
r
r
x = x(t )
r
oppure r = x(t )i + y (t ) j oppure
y = y (t )
Traiettoria
E’ il luogo dei punti occupati dal corpo durante il suo movimento
Velocità scalare
∆s spazio percorso
v sm =
=
media
∆t tempo impiegato
r
Velocità
r
∆r spostamento
v
=
vettoriale media m ∆t =
tempo
Velocità scalare
∆s
v s = lim
istantanea
∆t →0 ∆t
∆t → 0 significa tanto piccolo da poter considerare il moto uniforme
Curva
Grandezza scalare
Grandezza vettoriale
Grandezza scalare
Dato il grafico della velocità scalare in funzione del tempo, l’area sotto la curva
rappresenta lo spazio percorso
Velocità
vettoriale
istantanea (o più
semplicemente
velocità)
Accelerazione
r
r
∆r
v = lim
∆t →0 ∆t
∆t → 0 significa tanto piccolo da poter considerare il moto rettilineo e
uniforme
direzione
Tangente in ogni punto alla traiettoria
modulo
vs
verso
Del moto
r
r
r
∆v r
a = lim
= a tan gente + a normale
∆t →0 ∆t
r
a tan gente ≠ 0
r
a normale ≠ 0
Moto uniforme
Moto vario
Grandezza vettoriale
Grandezza vettoriale
Se il modulo della velocità cambia, cioè se il
moto non è uniforme
Se la direzione della velocità cambia, cioè se il
moto non è rettilineo
Moto in cui il modulo della velocità non varia nel tempo, non si ha alcuna informazione
sulla direzione
Moto in cui il modulo della velocità varia nel tempo, non si ha alcuna informazione sulla
direzione
2) I moti rettilinei
♦ Nei moti rettilinei è necessario fissare un asse di riferimento con origine e verso. Fatto questo, di tutte le
grandezze vettoriali si considerano solo le componenti cartesiane: componenti positive rappresentano vettori
nel verso del riferimento, componenti negative vettori nel verso opposto a quello del riferimento.
♦ Dato il grafico della legge oraria la pendenza della curva in ogni punto rappresenta la velocità nell’istante
corrispondente.
♦ Dato il grafico della componente della velocità, lo spostamento è la somma algebriche delle aree delle
regioni di piano individuate dal grafico della velocità, dall’asse orizzontale e dalle rette corrispondenti ai
tempi t1 e t2
Rettilineo uniforme
Accelerazione
a=0
2
velocità
v = cos tan te
Legge oraria
x = x0 + vt
Corso di recupero di Fisica classi seconde
a
v
x
t
t
t
Intercetta= posizione iniziale
Coefficiente angolare=velocità
Rettilineo uniformemente accelerato
accelerazione
a = cos tan te
velocità
v = v0 + at
a
Legge oraria
x = x0 + v0 t +
v
t
1
2
at 2
x
t
t
Intercetta= velocità iniziale
Coefficiente angolare=accelerazione
Intercetta= posizione iniziale
Pendenza iniziale della parabola = velocità iniziale
Concavità e apertura=accelerazione
3) I moti piani
Moto del proiettile
È composizione di:
un moto rettilineo uniforme (orizzontale)
un moto rettilineo uniformemente accelerato (verticale).
y
r
g
r
L’accelerazione è l’accelerazione di gravità g , verticale, verso il basso, di
modulo g ≈ 9,8 m / s 2
x
Rispetto ad un riferimento cartesiano come in figura si hanno le relazioni
seguenti
Accelerazione velocità
r v x = v 0 x
r a x = 0
v:
a:
v y = v0 y − gt
a y = − g
Legge oraria
x = v 0 x t + x0
r
r:
1 2
y = y 0 + v0 y t − 2 gt
v0 x e v0 y sono le componenti cartesiane della
velocità iniziale
3
Corso di recupero di Fisica classi seconde
La traiettoria che ne deriva è una parabola
L’accelerazione è costante
La componente orizzontale della velocità è costante.
La componente verticale della velocità cambia nel
tempo
Nel punto di massima altezza è nulla la componente
verticale della velocità.
r
g
Moto circolare uniforme
Traiettoria: circonferenza di raggio R
Moto periodico
periodo:
frequenza
velocità angolare
accelerazione
Centripeta di modulo costante
r
r v2
a = ω 2 R oppure a =
R
T
(tempo per compiere un giro completo)
1
T
∆ϑ 2π
ω=
=
= 2πf
∆t
T
velocità
f =
(giri compiuti nell’unità di tempo)
(radianti percorsi nell’unità di tempo)
Tangenziale, di modulo costante
r
v = ωR
Legge oraria
r x = R cos(ωt + ϑ 0 )
r:
y = R sin (ωt + ϑ 0 )
θ
CINEMATICA: esercizi
1) Dato il grafico v/t di un corpo che si muove di moto rettilineo:
a) determinare lo spazio percorso dopo 10 s
b) determinare il suo spostamento rispetto all’origine dopo 20 s
c) determinare la sua accelerazione tra 5 e 10 s
d) ricavare il grafico s/t
2) Dato il grafico della velocità in funzione del tempo di un corpo
che si muove di moto rettilineo:
a) Descrivi a parole il moto del corpo
b) Determina lo spazio percorso dopo 5 s
c) Determina il suo spostamento rispetto all’origine dopo 13 s
d) Determina la sua accelerazione tra 5 e 11 s
e) Ricava il grafico della legge oraria s = s(t) (2ASA)
4
Corso di recupero di Fisica classi seconde
3) I grafici v/t seguenti rappresentano i moti rettilinei di due
corpi A e B. Nell’istante iniziale B vede passare accanto a
sé A. Analizzando il grafico ricavare il tempo impiegato da
B per raggiungere A e lo spazio percorso. Rappresentare i
grafici s/t dei due moti sullo stesso piano cartesiano.
4) Due ciclisti A e B percorrono una stessa strada rettilinea,
mantenendo la velocità costante.
All’inizio dell’osservazione si trovano alla distanza di 30
km e si muovono uno verso l’altro con velocità di moduli rispettivamente pari a13 km/h e 20 km/h.
Rispetto ad un opportuno sistema di riferimento scrivi le leggi orarie dei due ciclisti e rappresentale in un
piano cartesiano. Determina: Quando e dove i ciclisti si incontreranno ? Quando i ciclisti si trovano a 5 km
di distanza l’uno dall’altro? Quando il ciclista più veloce ha percorso 10 km, dove s trova l’altro?
5) Un giocoliere lancia verticalmente una palla con una velocità iniziale di 6,60 m/s. Supponendo trascurabile
la resistenza dell’aria quale è l’altezza massima che raggiunge la palla rispetto al punto di lancio? Quanto
tempo rimane in volo prima di ritornare nel punto di partenza?
6) Una ragazza gioca a pallavolo. Si trova in battuta al limite del campo e colpisce la palla a 2,50 m da terra
imprimendole una velocità inclinata di 30° rispetto all’orizzontale e di modulo pari a 50 km/h. Rispetto ad
un opportuno sistema di riferimento (che indicherai) scrivi l’equazione cartesiana della traiettoria e
rappresentala. Rispondi poi alle seguenti domande (motivando):
a) la battuta supera la rete ?
b) la palla finisce nel campo avversario o è troppo lunga?
c) Quanto vale la velocità della palla nel punto più alto ? d) Con che velocità la palla tocca il suolo?
Le dimensioni di un campo di pallavolo sono di 9m x 9m (per ciascuna squadra) e la rete è alta 2,43 m.
7) Una ripresa televisiva mostra un calcio di rinvio del portiere di una squadra di calcio. Esaminando la ripresa
un tuo amico ha misurato la gittata del tiro, che risulta 66 m, e la durata del volo, che risulta 3,3 s. Un tuo amico
ti presenta questi dati e ti chiede se da essi si può avere un’idea della velocità e della direzione con cui è stato
calciato il pallone.
a) Come puoi modellizzare il moto del pallone? Quali ipotesi semplificative devi introdurre?
b) All’interno di queste ipotesi calcola la velocità con cui il portiere ha calciato il pallone.
c) Determina quale quota è stata raggiunta dal pallone nel punto di massima altezza della sua traiettoria e qual era il
valore della sua velocità in quell’istante. (2ASA)
8) Due proiettili vengono sparati entrambi con velocità di modulo 98 m/s , ma con direzione uno a 35° e l’altro
a 55° rispetto all’orizzontale. Calcola l’altezza massima raggiunta e la gittata di entrambi i proiettili. Da che
cosa dipende l’altezza massima raggiunta? Rappresenta graficamente tale dipendenza?
9) Un proiettile viene sparato dall’alto di una torre di 30 metri con la velocità di 200 m/s in direzione parallela
al suolo. Scrivi l’equazione della traiettoria rispetto ad un opportuno sistema di riferimento da indicare
nella figura. Calcola la gittata del proiettile e la velocità con cui tocca il suolo.
10) Durante la fase di centrifuga, il cestello di una lavatrice ruota a 1000 giri al minuto. Il cestello ha un
diametro di 56 cm. Calcola l’accelerazione centripeta in unità g che agisce sulla parte più esterna del
cestello.
11) Un’auto riesce a percorrere una curva se la sua accelerazione centripeta non supera il valore di 9.5m/s2.
Determinare il raggio della curva affinché la possa affrontare alla velocità di 80km/h.
12) Un satellite ruota attorno alla Terra su un’orbita praticamente circolare, con un periodo di 12 ore. Il raggio
4
dell’orbita è km 2,66 *10 . Calcola il modulo della velocità del satellite in km/h.
13) L'elica di un aereo, lunga ℓ = 0.80 m, ruota compiendo 20 giri al secondo; determinare
a) i moduli della velocità e dell'accelerazione della punta dell'elica;
b) la frequenza di rotazione necessaria perchè il modulo della velocità sia v = 800m/s;
5
Corso di recupero di Fisica classi seconde
c) come varia v se l'elica, mantenendo la stessa frequenza di rotazione, ha lunghezza doppia. (2ASA)
14) Un ragazzino fa roteare un sasso legato a una corda lunga ℓ = 0.8 m; sapendo che il modulo
dell'accelerazione centripeta è ac = 1.4m/s2, determinare
a) i moduli delle velocità angolare e lineare del sasso;
b) come variano i moduli delle velocità angolare e lineare del sasso se la corda fosse più corta di 10 cm e
l'accelerazione fosse la stessa. (2ASA)
DINAMICA: richiami teorici
Suggerimenti per la risoluzione di un problema di dinamica:
1) Fare il diagramma delle forze, cioè rappresentare graficamente tutte le forze agenti sul corpo o sui corpi
considerati.
Forza peso
Forza elastica
Reazione
normale
Tensione
Forza di attrito
radente
dinamico
Forza di attrito
radente statico
È la forza che la Terra (o qualunque altro pianeta)
esercita sui corpi in prossimità della sua superficie,
è un caso particolare di forza gravitazionale.
E’ sempre verticale verso il basso, è applicata al
baricentro del corpo
E’ la forza che una molla o un elastico esercita su
un corpo ad essa vincolato. Dipende dalle
caratteristiche della molla (k) e dalla sua
deformazione (x), è applicata al punto in cui il corpo
è fissato alla molla.
E’ l’unica forza esercitata da un piano liscio su un
corpo posto su di esso. E’ perpendicolare al piano e
uscente da esso, è applicata al baricentro della
superficie d’appoggio.
E’ la forza che una fune tesa esercita su un corpo ad
essa vincolato. E’ sempre diretta lungo la fune nel
verso opposto a quello del moto che la fune
impedisce o ostacola, è applicata al punto in cui il
corpo è vincolato alla fune
E’ la forza che un piano scabro esercita (oltre alla
reazione normale) su un corpo posto su di esso
quando il corpo è in movimento rispetto al piano.
Ha sempre direzione del moto e verso opposto.
Dipende dalle caratteristiche delle superfici a
contatto (kd) e dalla reazione normale esercitata dal
piano . E’ applicata al baricentro della superficie
d’appoggio.
E’ la forza che un piano scabro esercita su un corpo
posto su di esso quando il corpo è fermo rispetto al
piano e una forza esterna cerca di farlo muovere. Ha
sempre direzione del moto incipiente e verso
opposto. Dipende dalle caratteristiche delle
superfici a contatto (ks) e dalla reazione normale
esercitata dal piano (N). E’ applicata al baricentro
della superficie d’appoggio.
r
r
P = mg
r
r
Fel = − kx
la relazione è vettoriale, passando ai
moduli non si mette il segno -
Non esiste una formula di validità
generale, si determina a partire dal
secondo principio della dinamica.
Esiste un valore massimo oltre il
quale il vincolo si spezza.
Fatt din = k d N
r
La relazione è sui moduli; Fatt din e
r
N hanno direzioni diverse
Fatt sta ≤ k s N
r
La relazione è sui moduli; Fatt din e
r
N hanno direzioni diverse
r
r
2) Scrivere il secondo principio della dinamica applicato al problema in questione: R = ma Ricorda che il
secondo principio è espresso da una relazione vettoriale. Ricorda inoltre che se il corpo è in quiete o si
r
r
muove di moto rettilineo uniforme a = 0 , mentre in tutti gli altri casi a ≠ 0 .
3) Scomporre l’equazione vettoriale scritta lungo due assi scelti tra i tre seguenti:
6
Corso di recupero di Fisica classi seconde
Asse tangente
Asse normale
Asse binormale
E’ nella direzione del moto, con verso arbitrario. E’ da scegliere certamente quando il
corpo si muove di moto rettilineo, nel caso di moti curvilinei dipende
E’ l’asse nel piano del moto, perpendicolare alla traiettoria. E’ da scegliere certamente
nel caso di moti curvilinei, in questi casi infatti c’è certamente accelerazione normale
V2
che ha modulo: a normale =
R
E’ l’asse perpendicolare al piano del moto. Nei casi di moti piani (che sono gli unici
che ci interessano) lungo questa direzione non c’è accelerazione e dunque deve essere
nulla la componente della risultante delle forze.
4) Controlla il numero di equazioni e di incognite e risolvi il sistema.
DINAMICA: esercizi
1) Si consideri un punto materiale P avente massa m = 426 g appoggiato su un
piano inclinato liscio di altezza h = 24 cm e lunghezza ℓ = 64 cm; il punto
materiale è trattenuto da un filo fissato alla parte superiore del piano
inclinato, come in figura; determinare la tensione del filo. (2ASA)
2) Si consideri una carrucola su cui può scorrere un filo a cui sono appesi due
punti materiali P1 e P2 di masse m1 = 3,4 kg, m2 = 5,2 kg; determinare le
accelerazioni con cui si muovono P1 e P2 e la tensione del filo. (2ASA)
3) Un blocco di 800 kg è tirato con fune di massa trascurabile con una forza di
1600 N. Si calcoli l'intensità dell'accelerazione del blocco se l'attrito
corrisponde a 800 N. Calcola il coefficiente di attrito dinamico tra blocco e
superficie.
4) Un corpo è lanciato su un piano scabro inclinato di un angolo di 41 gradi rispetto all’orizzontale, con
velocità iniziale 8 m/s, verso l’alto. Il coefficiente di attrito dinamico tra il piano e il corpo vale 0,3. Si
calcoli l’accelerazione del corpo, dopo quanto tempo il corpo si ferma e la quota raggiunta.
5) Un pilota di bob di massa m1 = 70 kg spinge il suo bob che ha massa m2 = 12 kg su una superficie
orizzontale che ha che ha con il bob un attrito dinamico di coefficiente µd = 0.28 esercitando una forza di
modulo F = 150 N; determinare
a) il modulo a1 dell'accelerazione del bob finchè il pilota lo spinge;
b) il modulo a2 dell'accelerazione del bob quando il pilota ci salta sopra.
(2ASA)
6) Un corpo di massa m = 8.74 kg poggia su di un piano orizzontale scabro; su
di esso viene applicata una forza di trazione T avente modulo T = 60.6 N e
avente una direzione che forma un angolo α = 45◦ con l'orizzontale;
sapendo che il coefficiente di attrito dinamico fra le due superfici è µ =
0.62, determinare l’accelerazione del corpo e stabilire quale tipo di moto
descriverà il corpo. (2ASA)
7) Due casse sono poste a contatto su di un piano orizzontale privo di
attrito; le loro masse sono m1 = 2.4 kg e m2 = 3.6 kg; le casse sono
messe in movimento da una forza di modulo F = 12N che agisce sulla
prima cassa; determinare l'intensità Fc della forza di contatto agente fra
le casse e la loro accelerazione. (2ASA)
7
Corso di recupero di Fisica classi seconde
8) Un blocco di 28 kg è collegato a un secchio vuoto di massa 1,35 kg mediante
una corda che scorre su una carrucola priva di attrito. Il coefficiente di attrito
statico tra il tavolo e il blocco è 0,45 e il coefficiente di attrito dinamico tra il
tavolo e il blocco è uguale a 0,32. Il secchio viene gradualmente riempito di
sabbia fino a che il sistema inizia a muoversi.
a) Calcola la massa della sabbia versata nel secchio.
b) Calcola l’accelerazione del sistema. (2ASA)
9) Un corpo di peso 100N è premuto contro una parete da una forza F di 250N, perpendicolare
alla parete stessa. Se il coefficiente di attrito statico tra il corpo e la parete è di 0,4, il corpo
scivola o rimane in equilibrio?
10) Un libro è in equilibrio su un piano inclinato. Aumentando progressivamente l’inclinazione del piano il
libro comincia a scivolare nell’istante in cui l’altezza del piano è uguale a metà della base. Determina il
valore del coefficiente di attrito statico.
11) Un blocco di 8 kg e uno di 16 kg collegati da una fune scivolano lungo un piano inclinato di 30°. Il
coefficiente di attrito tra il blocco di 8 kg e il piano è 0,1, mentre quello tra il blocco di 16 kg e il piano è 0,2.
Determinare l’accelerazione dei blocchi e la tensione della fune supponendo che il blocco di 8 kg trascini
l’altro. Descrivere il moto se si cambiano di posto i due blocchi.
12) Un corpo di massa m=4 kg viene lanciato verso l’alto lungo un piano inclinato (altezza 2m, angolo di
inclinazione alla base 30°) con una velocità iniziale pari a 15 m/s. Quanto tempo impiega a giungere in cima
al piano inclinato ? Cosa accade quando è in cima al piano? In che modo prosegue la sua corsa?
8
Corso di recupero di Fisica classi seconde












