+ v

1
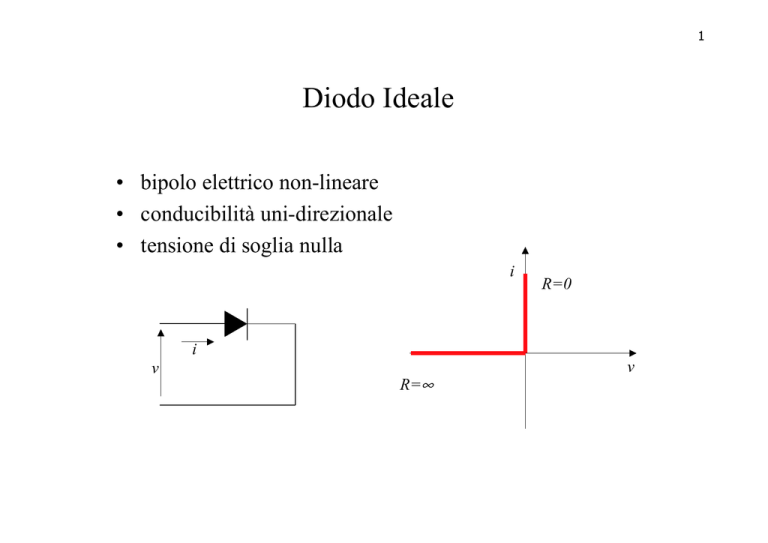
Diodo Ideale
• bipolo elettrico non-lineare
• conducibilità uni-direzionale
• tensione di soglia nulla
i
i
v
R=∞
R=0
v
2
esempi di applicazioni: D-R
Vi
+
+
vin
-
i
+
+
-
vout
-
t
V0
t
3
esempi di applicazioni: D-C
4
esempi di applicazioni: C-D
5
Diodo a Semiconduttore
• Le proprietà dei semiconduttori consentono di
realizzare strutture con proprietà di conducibilità
simili a quelle del diodo ideale
• Ingredienti:
– semiconduttori differentemente drogati
– giunzione
6
Giunzione p-n
• Modello Ideale:
– Facendo diffondere in un cristallo di Si, da un estremità
impurezze di tipo n e dall’altro impurezze di tipo p, si
ottiene un materiale da un lato n e dall’altro p.
– La superficie di separazione è detta giunzione
– Si supponga la concentrazione delle impurezze
costante.
Considerando le due parti separate. Esse sono NEUTRE
p
-
-
-
-
+
+
+
+
-
-
-
-
+
+
+
+
-
-
-
-
+
+
+
+
n
7
Corrente di Diffusione
• Poiché la concentrazione delle cariche libere è completamente
diversa nelle due regioni, nasce per la legge di Fick una corrente
di diffusione
p
-
-
-
-
+
+
+
+
-
-
-
-
+
+
+
+
-
-
-
-
+
+
+
+
n
– lacune dalla zona p attraversano la giunzione e si ricombinano
con gli elettroni della zona n
– elettroni dalla zona n attraversano la giunzione e si
ricombinano con le lacune della zona p
8
Regione di svuotamento
(depletion layer, regione di carica spaziale)
• Tale ricombinazione determina una diminuzione delle
cariche libere in un intorno della giunzione, detto regione di
svuotamento
• Tale regione, può essere pensata, in prima approssimazione,
come priva di cariche mobili e popolata solamente dagli ioni
delle impurezze.
• Il doppio strato di cariche da luogo ad un campo elettrico
(campo di built-in) che si oppone alla corrente di diffusione
Corrente di Drift
• Il campo E di built-in agevola il passaggio della
corrente di drift, costituita dalle cariche minoritarie in
ognuna delle due regioni.
• Il campo di built-in raggiunge un valore tale che la
corrente di drift eguaglia, in media, quella di
diffusione.
p
DL
- Vo +
A
+
B
-
-
-
-
-
-
-
-
-
-
-
Idrift = B+C
C
D
n
A corrente di diffusione (elettroni)
+
+
+
+
+
+
+
C corrente di drift (lacune)
+
+
+
+
D corrente di diffusione (lacune)
Idiff = A+D
E
B corrente di drift (elettroni)
9
10
Potenziale di contatto
• esempio per le lacune:
dV
dp
+ q ⋅ Dp
= 0;
dx
dx
= I diffusione ;
IP = p ⋅ q ⋅ µp
I drift
p ⋅ q ⋅µp
dV
dp
;
= −q ⋅ D p
dx
dx


KT
= 25mV/300K 
 VT =
q


D p = µ p ⋅ VT
µ
dp
dV
= − p dV = −
p
Dp
VT
NA
dp
1
=
−
∫ p VT
p no
p no
− Vo
∫ dV ⇒ V0 = VT ⋅ log
0
pno: concentrazione lacune nel
materiale n
NA: concentrazione di accettori:
concentrazione di lacune nel
materiale p
NA
p no
n i2
N N
=
⇒ V0 = VT ⋅ log A 2 D
ND
ni
N
A
= N D = 10 18 cm −3
n i = 10
10
cm
−3
V 0 ≅ 0.8V
11
Larghezza della regione di svuotamento
p
NA
n
Lp
Ln
ND
neutralità di carica : N A ⋅ L p = N D ⋅ L n
L = Lp + Ln
ND
Lp = L
;
NA + ND
NA = ND ⇒ Lp = Ln
NA
Ln = L
NA + ND
12
Campo di built-in
q
Se la regione di svuotamento è priva di cariche mobili:
•Nella regione p densità di carica fissa pari a q·NA
LP
•Nella regione n densità di carica fissa pari a q·ND
Dall’equazione
di Poisson
0 q⋅N
 Eo
D
=
dE
dx
∫
∫

ε
dE ρ  0
LN
= ⇒0
−LP
dx ε
 ∫ dE = ∫ − q ⋅ N A dx
E o
ε
0
q ⋅ NA
q ⋅ ND
E0 = −
LP = −
LN
ε
ε
LN
x
LN
x
E
LP
E0
V
Da cui:
V0
ε ⋅ E0  1
1 


+
L = LN + LP =
q  NA ND 
V(x ) = − ∫ E ⋅ dx ⇒ V0 = −
E0
(L P + L N )
2
x
LP
LN
13
Larghezza della regione di svuotamento
q ⋅ NA
q ⋅ ND
E0 = −
LP = −
LN
ε
ε
ε ⋅ E0  1
1 

;
L = LN + LP =
+
q  NA ND 
si ottiene
L= 2
ε ⋅ V0
q
considerando
E0 = 2
V0
L
 1
1 


+
 NA ND 
esempio :
N A = N D = 1017 cm −3 ⇒ L = L P = L N = 0.073 µm
N A = 1018 cm −3 ; N D = 1016 cm −3 ⇒ L P = 0.003 µm; L N = 0.323 µm;
14
Polarizzazione della giunzione pn
Polarizzazione Diretta
Polarizzazione Inversa
p
n
p
V
V
-
n
+
+
V’=V0+V
-
V’=V0-V
V’
V0
V0
V’
x
x
15
Polarizzazione Inversa
• La barriera di energia potenziale aumenta.
• La larghezza della regione svuotament aumenta.
• Diminuisce la corrente di diffusione e prevale quella di
drift
• La corrente è data dai portatori minoritari
– residuo dei portatori intrinseci
– quindi è di valore basso e poco dipendente da V
– ≈nA
• Cresce esponenzialmente con la temperatura
16
Tensione di Breakdown
• Al diminuire della tensione applicata, si possono
innescare fenomeni di rottura (breakdown)
caratterizzati da elevata corrente indipendente
dalla tensione
• Effetto Zener (effetto a due corpi)
– Aumento delle cariche minoritarie dovuto alla rottura
dei legami covalenti ad opera del campo elettrico
• Effetto Valanga (effetto a tre corpi)
– Rottura dei legami covalenti ad opera della energia
cinetica degli elettroni di drift
17
Polarizzazione diretta
• La barriera diminuisce favorendo l’aumento della
corrente di diffusione (movimento delle cariche
maggioritarie)
• La larghezza della regione di svuotamento diminuisce.
• La corrente diretta è funzione della tensione applicata e
dipende poco dalla temperatura
18
Concentrazione dei Portatori Minoritari
p n (0) = p n0 e
Dalla legge di Boltzmann si ottiene la
Legge della Giunzione
p
n p (0) = n p0 e
n
np0
V
V
VT
VT
pn0
x
np(0)
p
n
pn(0)
n`p(0)
np
pn
np0
p' n (x) = p' n (0) ⋅ e
p`n(0)
dove :
p' n (x) = p n (x) - p n 0
pn0
x
p
np
np0
n
pn
x
Lp
pn0
x
p' n (0) = p n (0) - p n 0
19
Livelli di energia dei semiconduttori p e n separati
EC
ED
EC
p
EF
n
EA
EV
EV
Livelli di energia dei semiconduttori p e n posti a contatto
χ Funzione
di affinità
EC
EF
EV
Livello di ionizzazione
φ0 Funzione
di lavoro
V0⋅q
20
Livelli di energia dei semiconduttori p e n posti a contatto e
polarizzati inversamente con una tensione V
EC
EF
EV
(V0+V)⋅q
Livelli di energia dei semiconduttori p e n posti a contatto e
polarizzati direttamente con una tensione V
EC
EF
EV
(V0-V)⋅q
21
Corrente in un diodo
Si considera il diodo polarizzato direttamente. In tale situazione le correnti relative ai
portatori minoritari sono fondamentalmente dovute alle componenti di diffusione.
In ogni sezione si ha la medesima corrente.
Si considera in particolare la sezione x=0 in cui Itot= Inp(0)+ Ipn(0).
p
n
+
Corrente totale
Corrente di drift
Ipn(0)
Ipp
(Lacune)
Inp(0)
Corrente di diffusione
(Elettroni)
Inp
Inn
Ipn
Corrente di drift
(elettroni)
Corrente di diffusione
(Lacune)
22


d n p (x)
d p n (x)

=
I Tot = I np (0) + I pn (0) = A ⋅ J np (0) + A ⋅ J pn (0) = A ⋅ q ⋅ D n ⋅
+ Dp ⋅

dx x =0
dx x = 0 

x
x


Lp
Ln


d n' p (x)
'
d
p
(x)
d
e
d
e
n
 = A ⋅ q ⋅  D n ⋅ n' p (0) ⋅
A ⋅ q ⋅ Dn ⋅
+ Dp ⋅
+ D p ⋅ p' n (0)⋅


dx
dx
dx
dx

x =0 

x =0

x =0

D
 V
 Dp
 V

 D n ⋅ n' p (0) D p ⋅ p' n (0) 
VT
VT
n






A⋅q⋅
+
= A⋅q⋅
⋅ n p0 ⋅ e − 1 +
⋅ p n 0 ⋅ e − 1  =


 Ln

 Lp


Ln
Lp







V


 V
 Dn
  V
Dp
V


T
T
A⋅q ⋅
I 0 ⋅ e − 1
⋅ n p0 +
⋅ p n0  ⋅ e − 1 =
L





Lp
 n
 





=


x =0 
•
Tale dimostrazione è valida anche nel caso di tensioni V negative con valore
assoluto molto maggiore di VT . In tale situazione risulta ITot =-I0.
•
I0 denominata corrente di saturazione inversa.
•
I0 è funzione di np0 e pn0 per cui risulta dipendente dalla teperatura.
Approssimativamente a I0 raddoppia per ogni incremento di temperatura pari 10°C.
•
Considerando anche i fenomeni di ricombinazone nella regione di svuotamento si
deve introdurre il fattore di non idealità η (Si => η=2 , Ge => η=1 ).
23
Equazione costitutiva del diodo
  V  
I = I0 ⋅ exp
 −1
  ηVT  
(mA)
Scale diverse
I0: corrente inversa
η: fattore di correzione
VT: tensione termica
Vγ
(µA)
(Volt)
inoltre:
VZ: tensione di breakdown
Vγ: tensione di soglia
Vγ@0.6 V per Si
(dipende da I)
24
Resistenza dinamica del diodo
A causa della curvatura variabile della caratteristica del diodo, la tangente alla curva
dipende dal punto di lavoro, cioè dalle coordinate I,V di tale punto. Il reciproco della
pendenza dellacaratteristica del diodo (dI/dV) viene detta resistenza dinamica (rd).
Partiamo dalla relazione caratteristica del diodo:
Derivando rispetto a V:
I ≅ Is
qV
q
q
dI
= Is
⋅ e kT = I ⋅
dV
kT
kT
Il termine KT/q è pari a circa 25 mV a
temperatura ambiente, per cui la resistenza
dinamica può essere espressa nel seguente
modo:
qV
e kT
⇒
kT
I⋅q
Id
rd ≅
∆Id
∆Vd
∆I d
Punto di
Lavoro
rd = 0.025/I in Ω ( I in A)
La resistenza dinamica è dipendente dalla
corrente continua di polarizzazione. Per
polarizzazioni inverse risulta:
rd @ ∞
rd =
∆Vd
Vd
25
Capacità del diodo
C (pF)
CT :(DEPLETION)
CD: (DIFFUSIONE)
CT
REGIONE
1
XC =
2 ⋅ π ⋅ f ⋅ C T ,D
rd
CD
REGIONE
5
P. INVERSA
-20 –15 –10
CD - CT
10
-5
P. DIRETTA
0
.25
.5
.75
Il comportamento del diodo
nei
confronti dei piccoli segnali, cioè di
variazioni di corrente o di tensione così
piccole da ritenere la rd costante, può
essere rappresentato da un circuito
come quello di figura.
26
circuiti con diodi
R=0.33KΩ
R=0.33KΩ
ID1
ID2
E=10V
E=10V
0.7V
ipotesi : VD1 = VD 2 = 0.7V
E −VD (10 −0.7 )V
=
= 28.18mA
I=
0.33KΩ
R
I
ID1 = ID2 = = 14.09mA
2
Se Idmax=20 mA un solo
diodo non potrebbe
sopportare tale valore.
0.7V
27
Selettore di Massimo
E1
E2
E1 = 10 V
E2 = 3 V
V0
R
ip. 1 D1 : on ⇒ V0 = 10 −0.6 = 9.4V ⇒ V D2 = 3 − 9.4 = −6.6V ⇒ D2 : off
ip. 2 D2 : on ⇒ V 0 = 10 − 3 = 7V ⇒ V D1 = 10 −7 = 3V impossibile!
a meno di Vγ l’uscita è il massimo tra i due ingressi
28
Selettore di Minimo
+V
R
E1
E1 = 10 V
E2
V0
E2 = 3 V
ip. 1 D1 : on ⇒ V0 = 10 + 0.6 = 10.6V ⇒ V D2 = 10.6 − 5 = 5.6V impossibile!⇒ D2 : off
ip. 2 D2 : on ⇒ V 0 = 5 + 0.6 = 5.6V ⇒ VD1 = 5.6 − 10 = −4.4V ⇒ D1 : off !
a meno di Vγ l’uscita è il minimo tra i due ingressi
29
Selettore di Massimo
Selettore di Minimo
E1
R
E2
V0
R
E1
E2
+V
E1
E2
V0
30
Circuito raddrizzatore ad una semionda
Vi
+
+
-
Vi
R
-
V0
V0
Vγ
t
31
raddrizzatore a doppia semionda
Vi
+
Vi
+
-
V0
R
V0
-
32
raddrizzatore doppia semionda
Vi
V0
R
V0
R
33
raddrizzatore con trasformatore a presa centrale
Vi
+
Vi
V0
R
+
-
V0
-
34
V0
R
V0
R
35
Diodo come elemento di Tracking
• Qualunque siano i valori di tensione e corrente, il
diodo in conduzione presenta ai suoi capi una
caduta di tensione pressochè fissa pari a V ≈0.6V
V1+n*0.6
0.6V
-4.4V
0V
0V
-5V
-0.6V
.
.
.
V1