LE COSTANTI FONDAMENTALI E IL SISTEMA SI
Franco Cabiati*, Anita Calcatelli*
Ricerche sono da tempo indirizzate verso una versione del Sistema Internazionale di
unità di misura (SI) interamente basato su invarianti fisici, con lo scopo di sostituire i
campioni materiali di tipo tradizionale con campioni naturali. Un tale sistema di unità di
misura offre grossi vantaggi alla metrologia perché le caratteristiche di indistruttibilità,
invariabilità, accessibilità e indipendenza dal luogo della misurazione sono senza dubbio
superiori a quelle di qualsiasi campione materiale. L'ulteriore tendenza a prediligere come
riferimento quegli invarianti che le teorie fisiche assumono come costanti fondamentali
comuni a più branche della metrologia aggiunge coerenza all'intero sistema delle unità.
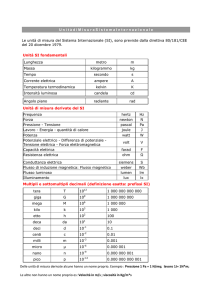
Riguardo all'unità di lunghezza (simbolo m), l'attuale definizione ("il metro è la
lunghezza del tragitto compiuto dalla luce nel vuoto in un intervallo di tempo di 1/299 792
458 di secondo") stabilisce il metro in termini del secondo e del valore assegnato per
definizione alla velocità della luce nel vuoto. Il passaggio dalla lunghezza d’onda (o dalla
frequenza, che essendo c costante esatta può essere convertita in lunghezza d’onda
senza aumentarne l’incertezza) al metro si attua mediante interferometri ottici.
L’unità di massa (simbolo kg) è l’unica che viene definita con riferimento ad un
campione materiale artificiale: il prototipo di platino/iridio conservato a Sèvres (“il
kilogrammo è l’unità di massa; essa è uguale alla massa del prototipo internazionale del
kilogrammo”). Un campione materiale presenta ovvii svantaggi: i rischi di danni o
addirittura di distruzione, la difficoltà della conservazione in uno stato ben definito, la
scarsa praticità di un riferimento unico a livello mondiale, le restrizioni imposte all'utilizzo
del campione dall'inevitabile usura. L'utilizzazione di bilance con incertezza di misura di
1 μg ha messo in evidenza tutti questi problemi e anche il fatto che il prototipo
internazionale del kilogrammo può presentare variazioni di 1 μg al mese, nei primi mesi
dopo che è stato pulito e lavato secondo particolari procedure oggetto di continuo studio e
revisione. Infatti le sostanze adsorbite dal prototipo vengono rimosse con operazioni di
lavaggio continuate finché viene meno la loro efficacia. Tuttavia, naturalmente,
l'adsorbimento riprende immediatamente, ed è tanto più veloce quanto più pulita è la
superficie. La necessaria operazione di pulizia induce quindi un periodo di instabilità e di
non definita conoscenza dello stato reale del prototipo, come di tutte le copie. Nel seguito,
in condizioni "stazionarie", l'adsorbimento è pari a circa 1 μg all'anno.
Per questo nel 1989, in occasione della terza verifica dei campioni nazionali, il CIPM
(Comité International des Poids et Mesures) raccomandò di considerare il kilogrammo
come la massa del prototipo internazionale subito dopo l'operazione di pulizia-lavaggio
secondo il metodo utilizzato dal BIPM (Bureau International des Poids et Mesures). Si
tratta di una raccomandazione e non di una ridefinizione. Naturalmente anche tutti i
campioni nazionali da confrontare vanno trattati nello stesso modo.
Una ridefinizione del kilogrammo direttamente legata al concetto classico di massa
potrebbe essere così enunciata: "il kilogrammo è la massa di N particelle nello stato
fondamentale, in quiete e non interagenti", dove si potrebbe identificare la particella con
l'elettrone, il protone o un particolare atomo. La continuità con l'attuale definizione sarebbe
data dalla relazione:
1
N=
mk
mx
=
mk
Mx
NA
dove mk denota la massa del prototipo internazionale del kilogrammo, mx ed Mx sono
rispettivamente la massa e la massa molare della particella scelta ed NA è la costante di
Avogadro.
Per adottare questa definizione è opportuno determinare NA ed Mx con un'incertezza
a livello di 10-8, per evitare che in futuro determinazioni più accurate delle relazioni tra
quelle costanti e il kilogrammo prototipo richiedano una variazione eccessiva del valore dei
campioni materiali usati nella pratica metrologica; questo livello non è stato ancora
raggiunto, però questa è una delle direzioni in cui attualmente opera la ricerca.
Presso alcuni laboratori metrologici, tra cui l'INRIM si impiega l'interferometria ottica
abbinata con quella a raggi X, per determinare il passo reticolare, e quindi il lato a0 della
cella elementare, di un monocristallo di silicio con purezza e composizione isotopica note.
Misurato per altra via il volume molare M / ρ sullo stesso monocristallo, si ottiene la
costante di Avogadro dalla relazione NA = 8 M / (ρ a03).
Altre ricerche vengono inoltre compiute per determinare NA con altri metodi, come
per esempio dalla relazione NA = F / e, dove F è la costante di Faraday (carica elettrica di
una mole di elettroni) ed e è la carica dell'elettrone.
Un altro tipo di ridefinizione dell’unità di massa discende da una visione più ampia
della realtà fisica implicata dalla massa, che include la teoria relativistica e in particolare
l’equivalenza con l’energia stabilita dall’equazione forse più celebre tra quelle dovute ad
Einstein: E = m c2, dove E è l’energia equivalente della massa m e c è la velocità di
propagazione delle onde elettromagnetiche nel vuoto. Il collegamento della massa agli
invarianti fisici è fornito dalla costante fondamentale più strettamente legata all’energia, la
costante di Planck h, attraverso l'equazione E = h f, dove f è la frequenza del fotone
corrispondente all'energia E. La relazione che da quelle equazioni deriva per la massa di
riferimento per l'unità, m = h f / c2, trova normalmente riscontro sperimentale nel mondo
delle particelle elementari. Quindi le diverse ipotesi di ridefinizione del kilogrammo che da
quella equazione derivano, pur avendo pieno significato teorico non corrispondono a
effettive possibilità di realizzazione dell’unità.
Un modo rivelatosi assai efficace di mettere in relazione una massa macroscopica,
dell’ordine del kilogrammo, con la costante di Planck è offerto dai campioni elettrici basati
sugli effetti Josephson e Hall quantistico. Infatti, combinando le equazioni più sotto
riportate per la definizione delle unità elettriche mediante questi due effetti, si ottiene una
potenza elettrica PE, di scala macroscopica, espressa in funzione di h e della frequenza
che interviene nel campione Josephson:
UJ2 1 2
= n i hf2
RH 4
Per riferire una massa ad h è dunque possibile confrontare un’energia o potenza
meccanica con una equivalente in forma elettrica, misurata per riferimento ai campioni
quantici. Questo confronto è appunto l’obiettivo principale di esperimenti messi in atto da
alcuni laboratori metrologici, i cui sistemi con denominazioni diverse (bilancia del watt,
bilancia con bobina in movimento, kilogrammo elettrico o elettronico, ecc.) consentono
nella sostanza la determinazione di h in termini di unità SI e quindi anche del kilogrammo.
L’equazione generalmente stabilita da questi esperimenti è
PE =
m g v = U I = kS h f 2
dove g è l’accelerazione di gravità (quindi m g è la forza peso), v è la velocità (di pochi
centimetri al secondo) impressa all’equipaggio mobile del sistema per determinare,
2
anziché calcolare come in passato, la costante di interazione tra bobina mobile e flusso
magnetico e kS è una costante adimensionale dipendente dal sistema di misura.
Sono attualmente in corso esperimenti per la determinazione sia di NA sia di h,
nell’intento di raggiungere il livello di incertezza necessario per una ridefinizione del
kilogrammo. Va notato inoltre che le due costanti sono legate tra loro dalla relazione
c α 2 Me 1
2 R∞ N A
dove α è la costante di struttura fine, Me la massa molare dell’elettrone e R∞ la costante di
Rydberg. Il vincolo tra h ed NA è reso particolarmente stretto dal fatto che le altre costanti
coinvolte sono conosciute con un valore dell’incertezza almeno un almeno un ordine di
grandezza minore di quella richiesta per una ridefinizione del kilogrammo. Ne consegue
che la ricerca per la determinazione di NA confluisce con quella per la determinazione di h
e i risultati dell’una costituiscono una verifica di quelli dell’altra.
h=
La definizione dell’unità di tempo (simbolo s) “il secondo è l'intervallo di tempo che
contiene 9 192 631 770 periodi della radiazione corrispondente alla transizione tra i due
livelli iperfini dello stato fondamentale dell'atomo di cesio 133” assume come riferimento
naturale, universale e costante nel tempo, l’atomo di cesio 133Cs non perturbato (cioè alla
temperatura termodinamica di 0 K). Gli orologi atomici a fascio di cesio che mantengono il
secondo presso l’iNRiM hanno incertezze relative di 10-14. Dal 2003 il campione primario
dell’Istituto si realizza mediante campioni di frequenza a fontana atomica che impiega
atomi di cesio raffreddati alla temperatura di 1μK con incertezze relative dell’ordine di
10-15.
Probabilmente ci sarà per il secondo, così come capita oggi per il metro, una
definizione di tipo generale, accompagnata da regole per la “mise en pratique”, da seguire
per la realizzazione dei campioni primari.
Spingendo l’incertezza nella definizione del secondo a valori sempre più piccoli, oltre
-17
10 , diventerà sensibile l'effetto della gravità terrestre e dovrà essere reso disponibile
come riferimento un orologio mantenuto in condizioni di microgravità, presenti nei
laboratori spaziali orbitanti.
La sfida attuale consiste nell’arrivare ad agganciare le frequenze coinvolte nella
definizione del secondo a quelle coinvolte nella definizione del metro. A quel punto, infatti,
fermo restando il valore esatto della velocità delle onde elettromagnetiche nel vuoto, le
unità secondo e metro potranno essere riferite ad una stessa transizione atomica.
Naturalmente dal miglioramento dei valori di incertezza delle unità di tempo e di
lunghezza si avvantaggerebbero anche tutte le unità da esse derivate.
L’unità di corrente elettrica (simbolo A) è definita attualmente attraverso
l’assegnazione, sia pure in modo implicito, di un valore fisso alla costante magnetica
(“l’ampere è l’intensità di una corrente costante che, mantenuta in due conduttori paralleli,
rettilinei, di lunghezza infinita, di sezione circolare trascurabile e posti alla distanza di 1
metro l’uno dall’altro nel vuoto, produrrebbe in questi conduttori una forza uguale a 2×10-7
newton per metro di lunghezza”). Infatti, in base alla teoria elettrodinamica, il sistema
ideale descritto dalla definizione produce la forza indicata solo assumendo per la costante
magnetica il valore μ0 = 4π×10-7. E’ tuttavia evidente che il sistema descritto non è
realizzabile se non mediante dispositivi con effetti elettrodinamici riconducibili, attraverso
la teoria, a quelli del sistema ideale. Le realizzazioni classiche dell’ampere sono sistemi in
forma di bilancia, che confrontano la forza elettrodinamica, prodotta per interazione tra
bobine percorse da corrente, con la forza peso di un campione di massa. L’accuratezza di
3
questi sistemi era comunque limitata dalla difficoltà di calcolare il rapporto tra forza e
corrente a partire dalle dimensioni e caratteristiche geometriche delle bobine.
Grazie a scoperte effettuate nella seconda metà del secolo scorso, la metrologia
delle grandezze elettromagnetiche è venuta a disporre di nuovi campioni naturali, utilizzati
per la riproduzione delle unità di tensione (effetto Josephson) e di resistenza (effetto Hall
quantistico).
Le giunzioni Josephson si presentano come convertitori naturali frequenza-tensione;
infatti quando due superconduttori, posti ad una distanza tale da consentire un processo di
tunnel da parte di una supercorrente (alcuni nanometri) vengono irradiati con una
radiazione elettromagnetica (microonda) di frequenza f, si viene a stabilire attraverso la
giunzione una tensione UJ (tensione Josephson) il cui valore quantizzato è dato dalla
relazione
UJ = n f h / 2e
dove n è un numero intero, h è la costante di Planck ed e è la carica dell'elettrone.
UJ non dipende dal materiale utilizzato, né dalle dimensioni o dalle tecniche
costruttive.
La costante KJ = 2e / h (detta costante di Josephson) si può utilizzare per definire un
"campione naturale" di tensione dipendente unicamente dall'unità di base nota con minore
incertezza (il secondo).
L'effetto Hall quantistico è un caso particolare di interazione elettrodinamica tra un
campo magnetico e una corrente tra loro perpendicolari. Esso trae importanza dal fatto di
consentire la riproduzione dell'unità di resistenza mediante l'aggancio alla resistenza
quantizzata di Hall
2
RH = h / i e
2
con i numero intero. L'aggancio è diretto perché la costante RK = h/e (detta costante di
von Klitzing) ha le dimensioni di una resistenza.
E’ interessante notare come uguagliando una tensione Josephson alla tensione prodotta
da una corrente elettrica I su una resistenza quantizzata di Hall si ottiene
I = UJ / RH = n i f e
dove la corrente è espressa dal numero n i f di cariche elementari (elettroni) al secondo.
A questa via per porre una corrente in rapporto con la costante fondamentale e se ne
affianca un’altra, più diretta, offerta dai dispositivi a singolo elettrone, che producono una
corrente elettrica (per ora assai piccola) come flusso di f cariche elementari al secondo,
dove f è la frequenza di un segnale elettrico ad alta frequenza che scandisce il passaggio
degli elettroni. La semplice relazione I = f e che ne deriva fornisce la base ideale per una
nuova definizione dell’ampere.
L'utilizzazione metrologica degli effetti quantici descritti è resa conveniente
essenzialmente dalla loro grande riproducibilità, che permette di ricavarne campioni con
stabilità molto maggiore dell’accuratezza con cui le costanti implicate sono conosciute in
unità SI. Nel 1990 sono stati assegnati, per convenzione, valori esatti alle costanti di
Josephson e di von Klitzing (rispettivamente KJ-90 e RK-90). I campioni di tensione e di
resistenza che adottano questi valori convenzionali hanno incertezze minori di 10-8.
4
Al presente, l’unità di temperatura (simbolo K) è definita con riferimento ad un
fenomeno naturale: la coesistenza delle tre fasi dell’acqua (“il kelvin, unità di temperatura
termodinamica, è la frazione 1/273,16 della temperatura termodinamica del punto triplo
dell'acqua”). Essa è tuttavia legata per definizione a una particolare proprietà di un
materiale che può presentare cause di deviazioni quali: possibili interazioni con il vetro del
contenitore, limitata purezza dell’acqua o presenza di isotopi degli elementi componenti.
Per il kelvin, fissato il valore della costante di Boltzman k, si potrebbe adottare la seguente
definizione: “il kelvin è la variazione di temperatura termodinamica che determina una
variazione di energia termica pari a 1,3806505x10-23 Joule”. Oggi il kelvin è realizzato con
incertezza nel campo di 10-7 e sarebbe opportuno che la ridefinizione mantenesse almeno
questo livello di incertezza, mentre k è ancora determinata con un’incertezza di 2x10-6. e
perciò si auspica un’ampia collaborazione di tutti gli istituti metrologici per arrivare ad una
migliore determinazione. Una delle strade più promettenti, a cui lavorano anche ricercatori
dell’INRIM, è quella della termometria acustica, basata sulla velocità del suono in un gas
puro (elio o argo). Questa è ricavata da misure di frequenza e di volume in risonatori
acustici di acciaio di tipo sferico, cioè di una forma regolare ben verificabile anche con
metodi interferometrici.
L'unità di quantità di sostanza (simbolo mol), la mole, è attualmente definita come
"la quantità di sostanza di un sistema che contiene tante entità elementari quanti sono gli
atomi in 0,012 kg di carbonio 12. Le entità elementari devono essere specificate e
possono essere atomi, molecole, ioni, elettroni, ecc. ovvero gruppi specificati di tali
particelle".
Quando si ha a che fare con reazioni chimiche e relative equazioni, è necessario
conoscere la quantità e la proporzione degli atomi e delle molecole che reagiscono. Data
la struttura atomica della materia, occorre quindi sapere quante particelle (individui chimici,
o entità elementari) sono contenute in una certa massa di sostanza, espressa in
kilogrammi. Da questa definizione segue che la massa di una mole di 12C è esattamente
eguale a 0,012 kg o, in modo equivalente, che la massa molare di 12C, M (12C), è eguale a
0,012 kg/mol. Il numero di entità per mole è, appunto, la costante di Avogadro NA
( ≈ 6,022x1023 mol-1), il che significa che in ogni mole di 12C ci sono NA atomi o ancora che
NA entità elementari sono contenute in una mole di qualsiasi sostanza.
Pertanto si potrebbe ridefinire la mole come ”la quantità di sostanza di un sistema
che contiene 6,0221415x1023 entità elementari”, dove il numero indicato corrisponde al
valore della costante di Avogadro, che verrebbe fissato esattamente. Al momento
dell’introduzione della nuova definizione, quello sarebbe anche il valore risultante dalle
migliori determinazioni del rapporto M(12C)/m(12C), mentre il valore di quello stesso
rapporto, non più implicato dalla definizione, diverrebbe oggetto di determinazione
sperimentale.
5
Infine l'unità di intensità luminosa (simbolo cd), attualmente definita come “l’intensità
luminosa, in una data direzione, di una sorgente che emette una radiazione
monocromatica di frequenza 540×1012 hertz e la cui intensità di radiazione in quella
direzione è 1/683 watt allo steradiante” (essendo lo steradiante l’unità di angolo solido), è
realizzata con riferimento al watt e si basa sulla capacità di misurare la potenza irradiata
da una sorgente laser mediante un radiometro criogenico con accuratezza migliore di
0,01% . Il fascio laser così misurato viene usato per tarare un fotometro campione, ossia
un rivelatore la cui risposta spettrale simula la risposta dell’occhio umano, caratterizzata
da una funzione della lunghezza d’onda V(λ). Il fotometro viene a sua volta usato per
determinare l’intensità luminosa (in candele) di una lampada ad incandescenza con
filamento di tungsteno con un’accuratezza di 0,1%.
Conclusione
L’attuale Sistema Internazionale di unità di misura fondato sulle sette unità di base
ha già diverse implicazioni con costanti fisiche fondamentali, alcune delle quali sono già
fissate dalle definizioni delle unità, come indica il diagramma di Fig. 1. L’estensione di
questo tipo di definizione ad altre unità è stato oggetto di proposte e di discussione a
partire dal 2005.
Delle diverse ipotesi di ridefinizione mediante riferimento ad una costante
fondamentale, quelle di alcune unità di base sono oggi concretamente raccomandate dagli
enti internazionali competenti per uno studio approfondito da parte dei laboratori
metrologici. In particolare esse riguardano: il kilogrammo, l’ampere, il kelvin e la mole. Un
possibile diagramma delle relazioni tra le attuali unità di base e i nuovi riferimenti, fissati
dalle ridefinizioni proposte, è mostrato in Fig. 2.
Infine la Conferenza Generale dei Pesi e Misure (organismo deliberante in materia)
nella riunione del 2007 ha raccomandato ufficialmente di considerare la possibilità di
ridefinire le suddette unità SI in funzione di costanti fondamentali e indica come tempo la
successiva riunione del 2011.
Figura 1. L’attuale Sistema Internazionale di unità di misura. Le unità di base (nei blocchi
circolari) sono rappresentate sotto i rispettivi riferimenti (nei blocchi quadrati), mentre le
6
frecce rappresentano le dipendenze funzionali stabilite dalla definizione di ciascuna unità
dai riferimenti e dalle altre unità di base.
Figura 2. Un possibile assetto del futuro SI secondo le nuove definizioni proposte per
alcune unità di base.
7
Bibliografia essenziale
Le Système International d’Unitès (SI), Bureau International des Poids et Mesures,
Paris, 1998.
Le BIPM et la Convention du Mètre, Bureau International des Poids et Mesures,
Paris, 1997.
C.J.Bordé, Base Units of SI, Fundamental Constants and Modern Quantum Physics,
Phil. Trans. Roy. Soc. A, in press (September 2005).
B.W. Petley, The fundamental constants and metrology, in Proceedings of the
international school of physics “Enrico Fermi”, course CXLVI “Recent advances in
metrology and fundamental constants”, Società Italiana di Fisica IOS Press Ohmsa,
Amsterdam, 2001, 121-155
M. Mills, P. J. Mohr, T. J. Quinn, B. N. Taylor and E. R. Williams, Redefiniton of the
kilogram: a decision whose time has come, Metrologia, 42 (2005) 71-80
R. L. Steiner, E. R. Williams, D. B. Newell and R. Liu, Towards an electric kilogram:
an improved measurement of the Plank constant and electron mass, Metrologia, 42 (2005)
431-441
CD multimediale, Il linguaggio delle misure, a cura di Anita Calcatelli – INRIM , 2006
(eventualmente richiedere a Elisabetta Melli- tel 011 3919524;e-mail:[email protected])
Franco Cabiati, Il Sistema Internazionale delle unità (SI) tra evoluzione e rivoluzione,
Atti della XXVI Giornata della Misurazione, Padova, 5-6 luglio 2007
Siti web utili
BIPM (Bureau International des Poids et Mesures): www.bipm.org
CODATA (Committee on Data for Science and Techonology of International Council for
Science) : www.codata.org
IUPAP (International Union for Pure and Applied Physics): www.iupap.org
IUPAC (International Union of Pure and Applied Chemistry): www.iupac.org
iNRiM (Istituto Nazionale di Ricerca Metrologica): www.inrim.it
*Ricercatori iNRiM
8