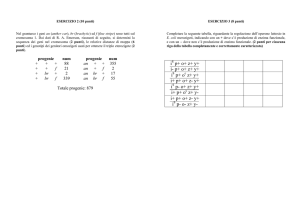
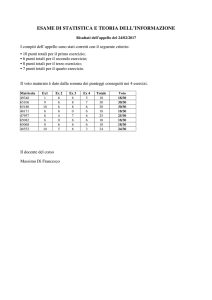
Chi-quadro
In generale, se
sono variabili aleatorie indipendenti con distribuzione
allora la variabile aleatoria
si distribuisce secondo una distribuzione Chi-quadro con k gradi di libertà
Chi-quadro
Dunque non ci stupisce che la quantità:
segua la distribuzione del
con opportuni gradi di libertà.
Ma allora se posso stimare il numero di casi attesi, ad esempio sulla base
di un modello probabilistico del sistema che sto studiando, allora posso
immediatamente costruire un test per la verifica delle ipotesi
Test di bontà di adattamento (goodness-of-fit test)
Goodness-of-fit
dati relativi all'anno 1999, USA
Giorno
NB bar-chart no distribuzione!
N. nati
Domenica
33
Lunedì
41
Martedì
63
Mercoledì
63
Giovedì
47
Venerdì
56
Sabato
47
Totale
350
NB errore nel libro Ven->Sab e Sab->Dom
In USA nascono più bambini il martedì e il mercoledì?
Goodness-of-fit
la probabilità di nascita è la stessa ogni giorno della settimana
la probabilità di nascita NON è la stessa ogni giorno della settimana
Modello sotto
le nascite sono proporzionali al numero di giorni della
settimana durante l'arco dell'anno 1999.
Nel 1999 ci sono stati 52 Domeniche, Lunedì,..., e 53 Venerdì. Dunque mi
attendo che:
Giorno
N. giorni
Proporzione di
giorni
Frequenza
attesa di nati
Domenica
52
0.142
49.863
Lunedì
52
0.142
49.863
Martedì
52
0.142
49.863
Mercoledì
52
0.142
49.863
Giovedì
52
0.142
49.863
Venerdì
53
0.145
50.822
Sabato
52
0.142
49.863
Totale
365
1
350
Goodness-of-fit
Giorno
N. OSSERVATO
nati
N. ATTESO nati
(Oss-Att)2/Att
Domenica
33
49.863
5.70
Lunedì
41
49.863
1.57
Martedì
63
49.863
3.46
Mercoledì
63
49.863
3.46
Giovedì
47
49.863
0.16
Venerdì
56
50.822
0.52
Sabato
47
49.863
0.16
Totale
350
350
15.05
NB no frequenze relative
Goodness-of-fit
Per un test goodness-of-fit:
7 giorni della settimana
il modello proporzionale NON ha
parametri liberi
NB il test può essere usato per ottenere il best-fit di un qualunque modello ai dati
Goodness-of-fit
Se fosse vera l'ipotesi nulla ci attenderemo:
più è marcata la differenza tra osservati e
attesi più è alto il valore di
Dunque consideriamo solo la coda più alta
Goodness-of-fit
Accettiamo dunque l'ipotesi alternativa: la probabilità di nascita NON è la
stessa per ogni giorno della settimana!
Perché?
NB l'analisi statistica dei dati è una cosa, il significato biologico un'altra!
Goodness-of-fit
Assunzioni:
●
i dati sono un campione casuale estratto dall'intera popolazione
●
nessuna delle categorie deve avere una frequenza attesa minore di 1
●
non più del 20% delle categorie deve avere frequenze attese minori di 5
possibile soluzione: raggruppare le categorie (e ricalcolare i gradi di libertà di
conseguenza)
Goodness-of-fit: 2 sole categorie
es. il progetto genoma umano ha individuato fino ad ora 20290 geni. Il
cromosoma X contiene il 5.2% del DNA, e sono stati identificati 781 geni.
Esistono su tale cromosoma tanti geni quanti ce ne attenderemmo se il numero
di geni fosse proporzionale alla quantità di DNA?
La percentuale dei geni umani sul cromosoma X è il 5.2%
La percentuale dei geni umani sul cromosoma X NON è il 5.2%
NB: potrebbe essere maggiore o minore
e dunque il test è a due code
Goodness-of-fit: 2 sole categorie
Ricordiamo che la distribuzione (discreta) binomiale descrive la probabilità
di avere k successi su n prove indipendenti con probabilità p in test
vero/falso, sì/no. Dunque sotto l'ipotesi nulla possiamo immediatamente
calcolare la probabilità che sul cromosoma X ci siano 0 oppure 1 oppure 2
oppure ...oppure k geni e sommare tra loro queste probabilità. Poiché il test è
a due code dobbiamo infine moltiplicare per 2.
Goodness-of-fit: 2 sole categorie
Ricordiamo che la distribuzione (discreta) binomiale descrive la probabilità
di avere k successi su n prove indipendenti con probabilità p in test
vero/falso, sì/no. Dunque sotto l'ipotesi nulla possiamo immediatamente
calcolare la probabilità che sul cromosoma X ci siano 0 oppure 1 oppure 2
oppure ...oppure k geni e sommare tra loro queste probabilità. Poiché il test è
a due code dobbiamo infine moltiplicare per 2.
NB errore nel libro, nota 6 pag.113
Dunque il fatto di aver osservato 781 geni sul cromosoma X è un fatto
davvero raro. Il numero di geni su questo cromosoma è significativamente
minore di quello che ci aspetteremmo in base alle dimensioni del
cromosoma.
Goodness-of-fit: 2 sole categorie
L'approccio che abbiamo seguito è rigoroso e esatto, ma assai laborioso. I conti
possono essere eseguiti solo con un computer (a meno di metterci tantissimo
tempo o impiegare tantissime persone).
Il metodo alternativo si basa sul test
es. il progetto genoma umano ha individuato fino ad ora 20290 geni. Il
cromosoma X contiene il 5.2% del DNA, e sono stati identificati 781 geni.
Esistono su tale cromosoma tanti geni quanti ce ne attenderemmo se il numero
di geni fosse proporzionale alla quantità di DNA?
La percentuale dei geni umani sul cromosoma X è il 5.2%
La percentuale dei geni umani sul cromosoma X NON è il 5.2%
Goodness-of-fit: 2 sole categorie
Cromosoma
Osservato
Atteso
781
1055
non-X
19509
19235
Totale
20290
20290
X
Goodness-of-fit: 2 sole categorie
...e arriviamo alla stessa conclusione che avevamo ottenuto usando la
distribuzione binomiale anche se con un certo margine di approssimazione
(ma con conti molto più semplici).
Goodness-of-fit: modello con 1 parametro
es. sappiamo che il sesso nella specie umana è una variabile indipendente (cosa
vuol dire?). Dunque ci attendiamo che in famiglie con 2 figli il numero di maschi
sia conforme ad una distribuzione binomiale con n=2 e p uguale alla probabilità di
avere un maschio in ogni singola prova (perché non assumiamo che p=0.5 visto
che il sesso dei figli è una variabile indipendente?)
È davvero così?
Due scienziati hanno analizzato i dati provenienti dal National Longitudinal Survey
of Youth (NLSY)
Totale
N. maschi
N. famiglie (con 2 figli)
0
530
1
1332
2
582
2444
Goodness-of-fit: modello con 1 parametro
Totale
N. maschi
N. famiglie (con 2 figli)
0
530
1
1332
2
582
2444
L'ipotesi non ci dice nulla riguardo alla probabilità di avere un figlio maschio, e
dunque dobbiamo cercare di calcolare questa probabilità a partire dai dati (ecco
il parametro!)
Goodness-of-fit: modello con 1 parametro
Il numero di maschi nelle famiglie con due figli segue la distribuzione binomiale
Il numero di maschi nelle famiglie con due figli NON segue la distribuzione binomiale
stimato dai dati
Dunque:
P di non avere figli maschi
P di avere 1 figlio maschio
P di avere 2 figli maschi
Usiamo questi valori per calcolare le frequenze attese
Goodness-of-fit: modello con 1 parametro
P di non avere figli maschi
P di avere 1 figlio maschio
P di avere 2 figli maschi
N. atteso di famiglie senza figli maschi
N. atteso di famiglie con 1 figlio maschio
N. atteso di famiglie con 2 figli maschi
Goodness-of-fit: modello con 1 parametro
N. maschi
N. osservato di
famiglie (con 2 figli)
N. atteso di famiglie
(con 2 figli)
0
530
587
1
1332
1221
2
582
636
2444
2444
Totale
n. categorie
n. parametri stimati in base ai dati
Concludiamo dunque che la distribuzione dei figli maschi (e delle femmine) non è
governata dalla distribuzione binomiale. Perché?
Chi-quadro: caso particolare
Tabelle di contingenza: tabella di frequenza per due o più variabili
categoriche che mostra come i valori di una variabile siano associati ai valori
di una seconda variabile.
es.
variabile esplicativa
variabile risposta
Gruppo di
controllo
Gruppo di
trattamento
Totale righe
Presenza
malattia
x11
x12
x11+x12
Assenza
malattia
x21
x22
x21+x22
x11+x21
x12+x22
x11+x12+x21+x22
Totale colonne
Chi-quadro: caso particolare
es. è stato osservato che certi pesci, se infestati da parassiti, trascorrono più tempo
vicino alla superficie dell'acqua e dunque possono essere predati da uccelli con più
facilità. Ci si chiede se questa ipotesi sia ragionevole.
L'infestazione parassitaria non determina un aumento della predazione e
dunque infestazione e predazione sono indipendenti
L'infestazione parassitaria determina un aumento della predazione e
dunque infestazione e predazione NON sono indipendenti
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
1
10
37
48
Non mangiati
dagli uccelli
49
35
9
93
Totali
(colonne)
50
45
46
141
Chi-quadro: caso particolare
L'infestazione parassitaria non determina un aumento della predazione e
dunque infestazione e predazione sono indipendenti
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
1
10
37
48
Non mangiati
dagli uccelli
49
35
9
93
Totali
(colonne)
50
45
46
141
dunque sotto l'ipotesi nulla (indipendenza tra le due variabili), e ricordando le
regole della probabilità, possiamo scrivere, ad es.:
e così per tutte le celle della tabella. Possiamo stimare le probabilità dai dati
Chi-quadro: caso particolare
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
1
10
37
48
Non mangiati
dagli uccelli
49
35
9
93
Totali
(colonne)
50
45
46
141
esercizio: calcolare la probabiltà condizionata
Chi-quadro: caso particolare
1
43
47
49
47
49
1
1
43
Chi-quadro: caso particolare
Si noti che:
dunque:
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
1
10
37
48
Non mangiati
dagli uccelli
49
35
9
93
Totali
(colonne)
50
45
46
141
Chi-quadro: caso particolare
Osservati
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
1
10
37
48
Non mangiati
dagli uccelli
49
35
9
93
Totali
(colonne)
50
45
46
141
Attesi
Mangiati dagli
uccelli
Non infestati
Poco infestati
Tanto infestati Totali (righe)
17
48
Non mangiati
dagli uccelli
Totali
(colonne)
93
50
45
46
141
Chi-quadro: caso particolare
Osservati
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
1
10
37
48
Non mangiati
dagli uccelli
49
35
9
93
Totali
(colonne)
50
45
46
141
Attesi
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
17
15.3
15.7
48
Non mangiati
dagli uccelli
33
29.7
30.3
93
Totali
(colonne)
50
45
46
141
Chi-quadro: caso particolare
Oss., Att.
Non infestati
Poco infestati
Tanto infestati Totali (righe)
Mangiati dagli
uccelli
1, 17
10, 15.3
37, 15.7
48
Non mangiati
dagli uccelli
49, 33
35, 29.7
9, 30.3
93
50
45
46
141
Totali
(colonne)
Rifiutiamo quindi l'ipotesi nulla, ovvero che
predazione e infestazione siano indipendenti
Chi-quadro: caso particolare
Chi-quadro: caso particolare
Assunzioni:
●
campionamento casuale e campioni indipendenti
●
non più del 20% delle celle possono avere una frequenza attesa minore di 5
●
nessuna cella può avere una frequenza attesa minore di 1
Correzioni:
●
nel caso di una tabella di contingenza 2X2 è raccomandato l'uso della
correzione di Yates per la continuità (ma attenzione che riduce la potenza
del test)
Violazione assunzioni:
●
usare il test esatto di Fisher
This work is licensed under a Creative Commons AttributionNonCommercial 4.0 International License.
see: http://creativecommons.org/licenses/by-nc/4.0/
Roberto Chignola
Università di Verona
[email protected]