Compito del 29 gen. 2004

Facoltà di Ingegneria
II Prova in Itinere di Fisica I (*)
29 Gennaio 2004
Quesito n. 1
m1
M, R
Piano liscio
θ
m2
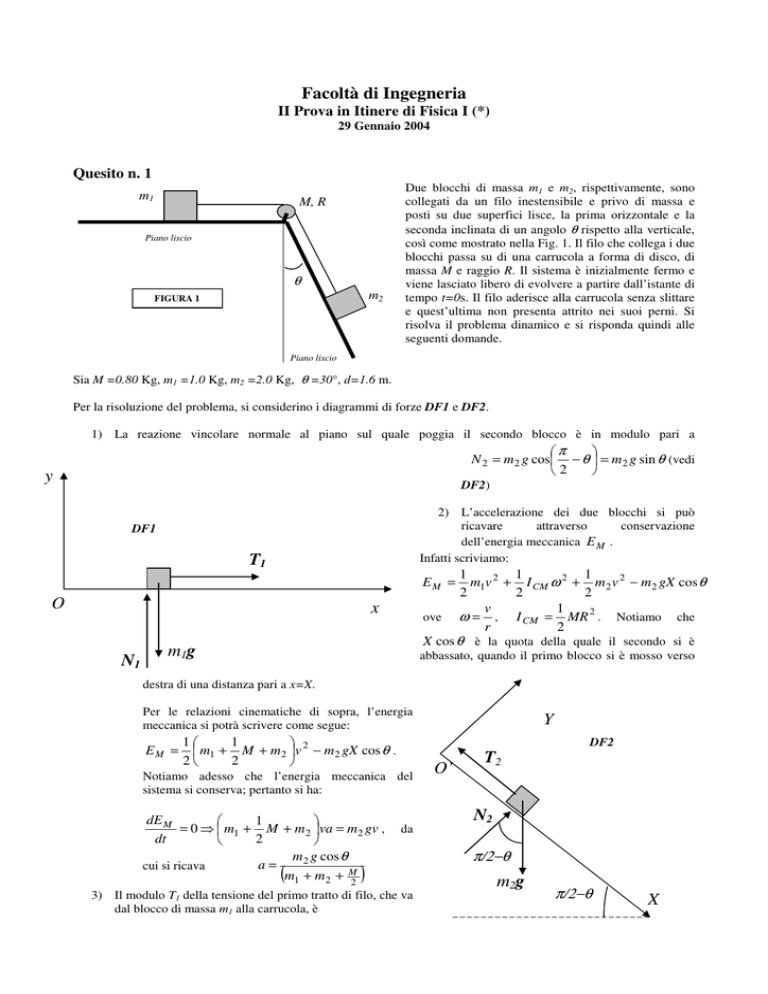
FIGURA 1
Due blocchi di massa m1 e m2, rispettivamente, sono
collegati da un filo inestensibile e privo di massa e
posti su due superfici lisce, la prima orizzontale e la
seconda inclinata di un angolo θ rispetto alla verticale,
così come mostrato nella Fig. 1. Il filo che collega i due
blocchi passa su di una carrucola a forma di disco, di
massa M e raggio R. Il sistema è inizialmente fermo e
viene lasciato libero di evolvere a partire dall’istante di
tempo t=0s. Il filo aderisce alla carrucola senza slittare
e quest’ultima non presenta attrito nei suoi perni. Si
risolva il problema dinamico e si risponda quindi alle
seguenti domande.
Piano liscio
Sia M =0.80 Kg, m1 =1.0 Kg, m2 =2.0 Kg, θ =30°, d=1.6 m.
Per la risoluzione del problema, si considerino i diagrammi di forze DF1 e DF2.
1) La reazione vincolare normale al piano sul quale poggia il secondo blocco è in modulo pari a
N 2 = m 2 g cos
y
π
2
− θ = m 2 g sin θ (vedi
DF2)
2) L’accelerazione dei due blocchi si può
ricavare
attraverso
conservazione
dell’energia meccanica E M .
Infatti scriviamo:
DF1
T1
EM =
O
x
N1
ove
1
1
1
m1v 2 + I CM ω 2 + m 2 v 2 − m2 gX cos θ
2
2
2
v
1
ω = , I CM = MR 2 . Notiamo che
r
2
X cos θ è la quota della quale il secondo si è
abbassato, quando il primo blocco si è mosso verso
m1g
destra di una distanza pari a x=X.
Per le relazioni cinematiche di sopra, l’energia
meccanica si potrà scrivere come segue:
EM =
1
1
m1 + M + m 2 v 2 − m 2 gX cos θ .
2
2
Notiamo adesso che l’energia meccanica del
sistema si conserva; pertanto si ha:
dE M
=0
dt
cui si ricava
m1 +
1
M + m 2 va = m 2 gv ,
2
m 2 g cos θ
a=
m1 + m 2 + M2
(
da
)
3) Il modulo T1 della tensione del primo tratto di filo, che va
dal blocco di massa m1 alla carrucola, è
Y
O’
T2
DF2
N2
π/2−θ
m2g
π/2−θ
X
T1 = m1a =
m1 m 2 g cos θ
(m1 + m2 + M2 ) (vedi DF1).
4) Il modulo T2 della tensione del secondo tratto di filo, che va dalla carrucola al blocco di massa m2, si può
calcolare tenendo presente le componenti lungo il piano inclinato delle forze agenti sul blocco mostrato in DF2.
Pertanto, lungo X, si ha
− T2 + m2 g sin
(π2 − θ ) = m2 a ,
cosicché, risolvendo per T2 , si ottiene:
(m1 + M2 )m2 g cos θ
T2 = m2 (g cos θ − a ) =
(m1 + m2 + M2 )
5) La velocità V del primo blocco, dopo che quest’ultimo si è spostato di distanza d dal punto di partenza sul piano
orizzontale si può calcolare tenendo presente l’espressione dell’energia meccanica del sistema
EM =
1
1
m1 + M + m2 v 2 − m 2 gX cos θ .
2
2
Sostituendo per X il valore d ed eguagliando tutto a zero, infatti si ha:
V=
2m 2 gd cos θ
.
1
m1 + M + m 2
2
Quesito n. 2
FIGURA 2
M
m
R
θ
risponda quindi alle seguenti domande.
Sia M =2.00 Kg, θ =30°.
Il sistema rappresentato in Fig. 2 consta di un
disco, di massa M e di raggio R, che può rotolare
senza strisciare su di un piano inclinato di un
angolo θ rispetto all’orizzontale, di una carrucola
ideale e di un blocco di massa m. Il disco viene
tirato da un filo inestensibile e privo di massa,
che è legato da un estremo ad un gancio di massa
trascurabile, così come mostrato nel riquadro
sinistro della Fig. 2, e dall’altro estremo al
blocco. Si noti che il gancio è tale da non
produrre attrito sul disco, quando quest’ultimo è
in rotazione. Si risolva il problema in condizioni
statiche e dinamiche, indicando con m0 il valore
di m per il quale il sistema è in equilibrio, e si
6) Il valore m0 della massa del blocco che permette al disco di mantenersi in equilibrio sul piano inclinato si trova
attraverso le condizioni seguenti (si veda
DF3
il diagramma di forze DF3):
a) la somma delle forze sul blocco è nulla,
T=m0g
ovvero:
T = m0 g ;
ft
θ
N
Mg
b) la somma dei momenti rispetto al punto di
contatto tra il disco è il piano è nulla, ovvero:
(Mg sin θ )R − TR = 0
cosicché si ha m 0 = M sin θ .
7) Il modulo T0 della tensione nel filo quando il sistema è all’equilibrio vale T = m0 g , come si è detto prima.
8) In condizioni dinamiche, l’accelerazione a del blocco (positiva verso il basso) si trova risolvendo le seguenti
equazioni della dinamica, scritte, rispettivamente, per il blocco e per il disco:
− T + mg = ma ;
TR − (Mg sin θ )R = I P α
ove I P =
3
a
m − M sin θ
MR 2 e α = . Risolvendo per l’accelerazione a, si ha a =
g.
2
R
m + 32 M
9) La tensione T nel filo si trova adesso risolvendo una delle due equazioni della dinamica di sopra per T,
cosicché:
T = m( g − a ) =
mM
(32 + sin θ )
m + 32 M
g.
10) Il modulo ft della forza di attrito tra il disco e il piano inclinato si può trovare ricorrendo, ad esempio, al teorema
del centro di massa e scrivendo, per il disco:
F ext = Ma CM .
Nella direzione parallela al piano si ha:
T − f t − Mg sin θ = Ma .
Risolvendo adesso per f t , troviamo f t =
M (m − M sin θ )
g.
2m + 3M
Quesito n. 3
Un piccolo blocco di massa m può scivolare
senza attrito sulla superficie interna di una guida
sagomata a mo’ di quarto di circonferenza avente
raggio R (Fig. 3). Il blocchetto parte da fermo
dalla sommità A della guida e raggiunge, nel
punto B, con velocità VB, un tratto di piano
orizzontale scabro di lunghezza R. Superato
questo tratto di piano scabro, in C raggiunge, con
velocità VC, un tratto di piano liscio, in fondo al
quale è posta una molla ideale di costante elastica
k. Il coefficiente di attrito dinamico tra il blocco e
il tratto di piano scabro è µ. Si trovino le quantità
cinematiche di rilievo nel problema e si risponda
quindi alle seguenti domande.
FIGURA 3
A
M
m
R
k
R
C
B tratto di piano scabro
tratto di piano liscio
Sia m=0.500 Kg, R =1.00 m, k=300 N/m, µ=0.500.
11) La velocità VB del blocchetto si calcola attraverso conservazione dell’energia, scrivendo:
( A)
( B)
EM
= EM
cosicché si ha V B = 2 gR .
mgR =
1
mV B 2 ,
2
12) Il modulo a dell’accelerazione del blocchetto sul tratto di piano scabro si trova applicando la seconda legge di
Newton. Nella direzione del moto (direzione x) e in quella normale al piano (direzione y) si ha (vedi anche
DCL1):
x)
y
y)
DCL1
N = mg
E’ possibile adesso scrivere la relazione fenomenologia seguente, che
ci permette di definire la forza di attrito f t in termini della relazione
ft
O
x
N
− f t = ma x
mg
vincolare N in condizioni dinamiche:
f t = µN .
Tenendo conto delle relazioni di sopra, si può pertanto scrivere
a x = − µg , cosicché a = µg .
13) Il modulo della forza di attrito sul blocchetto nel tratto di piano scabro, così come visto sopra, vale f t = µN .
14) La velocità VC del blocchetto si può ottenere mediante la relazione cinematica seguente:
1 2 1 2
VC − V B = 2 a x R ,
2
2
cosicché, sostituendo gli opportuni valori per ax e VB e risolvendo per VC, si ottiene:
VC = 2(1 − µ )gR .
15) La massima compressione d della molla viene adesso calcolata attraverso conservazione dell’energia, scrivendo
(C )
( D)
EM
= EM
1
1
mVC 2 = kd 2 , ove indichiamo con D il punto in cui il blocchetto si arresta, comprimendo la
2
2
molla, appunto, di un tratto d. Sostituendo per VC e risolvendo per d, si ha
d=
2(1 − µ )mgR
.
k
(*) I dati nella prova sono quelli relativi al compito A. Le soluzioni sono state riportate solo in forma analitica.