Schemi a blocchi
Gli schemi a blocchi costituiscono un
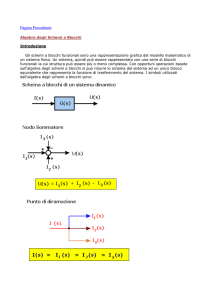
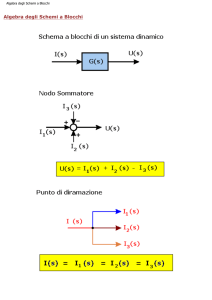
Nodo sommatore
semplice ed efficace metodo di
rappresentazione di un sistema, a partire
Punto di derivazione
Fig.1.1
dalle equazioni del corrispondente
modello matematico, formulato mediante
S +
_
l’introduzione di opportune variabili di
E
U
G
U
ingresso, di uscita ed interne.
Nell’esempio sottostante si trovano i
quattro elementi base, costitutivi degli
Blocco
Rami
schemi a blocchi: rami, blocchi,
sommatori e punti di derivazione.
u(s)
G(s)
y(s)
1. Ai rami sono associate le variabili di ingresso, di uscita ed interne.
2. Ai blocchi sono associate le funzioni di trasferimento fra le variabili entranti e quelle uscenti
dal blocco stesso.
3. La variabile associata al ramo di uscita di un sommatore è data dalla somma algebrica delle
variabili entranti.
4. I punti di derivazione o, di diramazione, provvedono a trasferire su diversi rami di uscita
(senza apportare modifiche) la variabile di ingresso.
(quindi a valle di un punto di diramazione, il segnale è sempre lo stesso su tutti i rami in
uscita)
5. un nodo sommatore esegue una operazione di somma algebrica tra due o più segnali. Si
osservi che ogni segnale entrante è nel nodo è caratterizzato da un segno (±) che essenziale
riportare sulla somma algebrica.
Regole di algebra dei blocchi
Esistono regole di algebra dei blocchi che permettono di ridurre schemi complessi a strutture
semplici, per le quali risulta agevole il calcolo della funzione di trasferimento fra la variabile
assunta come ingresso del sistema e quella considerata come uscita.
Le trasformazioni ed equivalenze di seguito riportate riassumono alcune fra le regole principali,
che possono essere applicate direttamente o combinate fra loro per la riduzione di schemi ed il
calcolo di funzioni di trasferimento.
N.B.: I blocchi degli schemi di seguito riportati sono relativi a sistemi ad un ingresso ed
un’uscita, ovvero i segnali associati ai rami sono scalari.
Algebra dei blocchi Paolo Patti
1
Simbologia degli schemi a blocchi
x
Simbolo
Blocco
A
x
x
Punto di diramazione o di derivazione. ( Lo stesso segnale in ingresso al
nodo si dirama e si ritrova nelle uscite)
x
+
Segnale “informazione”
v
x +
y
Nodo di somma (sommatore) y=x+v+z
+ z
y
x+
-
Nodo di comparazione o confronto y=x-z
z
Relazione fra i simboli
x
y
A
y=A·x
1. Blocchi in cascata o in serie (Cascata di blocchi)
Due o più blocchi si dicono in serie quando l’uscita di uno costituisce l’ingresso
dell’altro.
x
m=A·x
A
m
B
y
x
y=B·m => y=A·B·x posto A·B=G =>
G
y
y=G·x
Più blocchi in serie si possono sostituire con un unico blocco avente f.d.t. pari al prodotto della
singole f.d.t. dei blocchi in serie.
Il prodotto gode della proprietà commutativa A·B= B·A
Algebra dei blocchi Paolo Patti
2
2.
Blocchi in parallelo
m
A
x
y
+
+
x
A +B
y
x
G
y
n
B
Nodo di
somma
m=A·x
n=B·x
y=m+n=A·x+B·x=(A+B)x= G·x
posto
A+B=G quindi y=G·x
Due o più blocchi si dicono in parallelo quando hanno il medesimo ingresso, mentre le uscite sono
sommate algebricamente (vale anche per loro la proprietà commutativa). ±A±B=±B±A
A
x
-
B
+
y
x
A –B+C
x
y
G
+
(A-B+C)=G
y=G·x
Notare come la somma è algebrica e come si
riportano fedelmente i segni in ingresso al nodo
C
3.
Blocchi in retroazione (Anello di retroazione)
(Avanzamento)
x
e
A
y
u(s)
z
A
1+ A⋅ B
y(s)
B
(Retroazione)
z=B·y
e=x-z
y=(x-z)·A
y=(x-B·y)·A
y=Ax-ABy
y+ABy=Ax
e·A=y
x
A
G =
1+ A⋅ B
G
y=Gx
Algebra dei blocchi Paolo Patti
A
y=
⋅ x
1+ A⋅ B
y(1+AB)=Ax
3
y
y
4. Spostamento di un punto di derivazione a monte di un blocco
y
x
A
y
x
A
y = A⋅ x
y = A⋅ x
y
y = A⋅ x
A
y = A⋅ x
Il blocco di compensazione deve essere uguale al blocco principale
5. Spostamento di un punto di derivazione a valle di un blocco
y
x
x
A
A
y = A⋅ x
y = A⋅ x
x
y
y = A⋅ x
1
A
Il blocco di compensazione deve essere
uguale all’inverso del blocco principale
x =
1
1
⋅ y =
⋅ A ⋅x = x
A
A
6. Spostamento di un blocco rispetto ad un nodo sommatore
x
A
±
±
v
x
y
±
±
v
B
A
y
B/A
Fig. a
x
v
A/B
±
±
B
Fig. b
In fig. a per spostare A dal ramo 1 a dopo il sommatore dividiamo per A sia nel ramo 1 che nel
A
sparisce
ramo due e otteniamo rispettivamente
= 1 , quindi il blocco
A
A
B
Nel ramo due dividendo per lo stesso A, avremo
a posto di A , l’uscita invece la dobbiamo
A
moltiplicare per A Analogamente nella fig. b si sposta il blocco B
B
Algebra dei blocchi Paolo Patti
4
y
7. Spostamento di un blocco rispetto ad un punto di derivazione
y
A
x
x
y
A/ B
B
B
z
z
Fig. a
y1(s)
x
A
B/A
y2(s)
Fig. b
In fig. a per spostare B dal ramo 2 da dopo a prima del nodo di diramazione dividiamo per
B
B sia nel ramo due che nel ramo uno e otteniamo rispettivamente = 1 , quindi il blocco
B
A
B sparisce dal ramo due. Nel ramo uno dividendo per lo stesso B, avremo
a posto di A,
B
l’ingresso invece lo dobbiamo moltiplicare per B
Analogamente nella fig. b si sposta il blocco A
Bibliografia
Algebra dei blocchi da prof. Marina Indri Dip. di Automatica e Informatica Politecnico di Torino Versione 1.1
Savi - Tanzi - Nasuti _ed Calderoni Sistemi, autom. e org. prod.
Algebra dei blocchi Paolo Patti
5