Esame di Fondamenti di Elettromagnetismo 30 Settembre 2008 Ancona
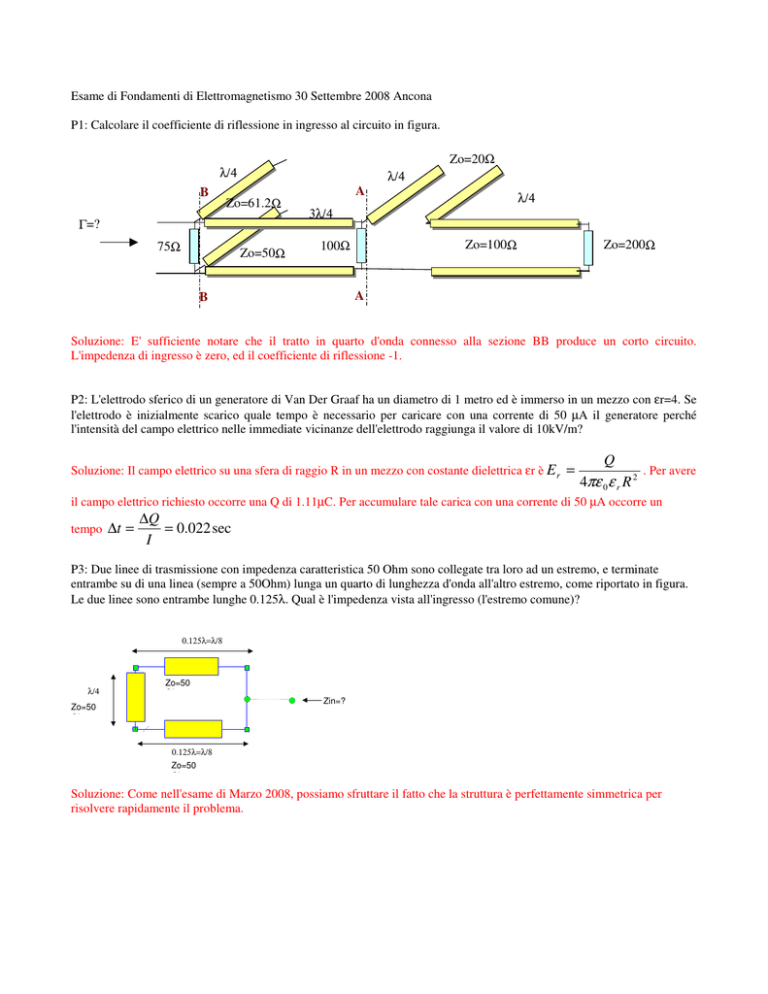
P1: Calcolare il coefficiente di riflessione in ingresso al circuito in figura.
Zo=20Ω
λ/4
λ/4
A
B
Zo=61.2Ω
Γ=?
75Ω
Zo=50Ω
λ/4
3λ/4
Zo=100Ω
100Ω
Zo=200Ω
A
B
Soluzione: E' sufficiente notare che il tratto in quarto d'onda connesso alla sezione BB produce un corto circuito.
L'impedenza di ingresso è zero, ed il coefficiente di riflessione -1.
P2: L'elettrodo sferico di un generatore di Van Der Graaf ha un diametro di 1 metro ed è immerso in un mezzo con εr=4. Se
l'elettrodo è inizialmente scarico quale tempo è necessario per caricare con una corrente di 50 µA il generatore perché
l'intensità del campo elettrico nelle immediate vicinanze dell'elettrodo raggiunga il valore di 10kV/m?
Soluzione: Il campo elettrico su una sfera di raggio R in un mezzo con costante dielettrica εr è E r
=
Q
4πε 0 ε r R 2
. Per avere
il campo elettrico richiesto occorre una Q di 1.11µC. Per accumulare tale carica con una corrente di 50 µA occorre un
tempo
∆t =
∆Q
= 0.022 sec
I
P3: Due linee di trasmissione con impedenza caratteristica 50 Ohm sono collegate tra loro ad un estremo, e terminate
entrambe su di una linea (sempre a 50Ohm) lunga un quarto di lunghezza d'onda all'altro estremo, come riportato in figura.
Le due linee sono entrambe lunghe 0.125λ. Qual è l'impedenza vista all'ingresso (l'estremo comune)?
0.125λ=λ/8
λ/4
Zo=50
Ohm
Zin=?
Zo=50
Ohm
0.125λ=λ/8
Zo=50
Ohm
Soluzione: Come nell'esame di Marzo 2008, possiamo sfruttare il fatto che la struttura è perfettamente simmetrica per
risolvere rapidamente il problema.
λ/8
λ/8
Zo=50
Ohm
Zin=?
λ/8
λ/8
Zo=50
Ohm
Il piano di simmetria è evidenziato dal tratteggio. In pratica quindi il circuito di riduce al parallelo di due linee identiche
lunghe ciascuna 2λ/8=λ/4: a causa della perfetta simmetria i due estremi della linea lungo il tratteggio sarebbero
equipotenziali anche tagliando la struttura lungo il tratteggio stesso (se all'ingresso le due linee sono stimolate con la stessa
tensione [metà superiore e metà inferiore del disegno], per simmetria anche in uscita avremo la stessa tensione alle due
metà). Quindi il circuito può essere visto come il parallelo di due linee lunghe un quarto d'onda lasciate aperte, e ciascuna
produce in ingresso un corto circuito. Quindi l'impedenza di ingresso è banalmente zero (solo alla frequenza a cui
chiaramente le linee hanno la lunghezza d'onda del problema e a multipli! Altrimenti sarà un'impedenza puramente reattiva,
capacitiva per frequenze inferiori e induttiva per frequenze superiori).
P4: Quanto lavoro si deve compiere per collocare una carica di 1µC a 1cm da un piano conduttore, partendo dall’infinito ?
Soluzione: Il lavoro che si deve compiere corrisponde all'energia potenziale del sistema di cariche: nel nostro caso il
sistema di cariche è, per via del teorema delle immagini, un dipolo le cui cariche distano 2 cm. Nella lezione 9 questa è stata
calcolata e nel caso semplice di due cariche è semplicemente
U12 =
Q1Q2
Si ottiene una energia pari a -0.449 J.
4πεr12
P5: Un disco di rame di raggio 10cm ruota a 1200 giri al minuto in senso antiorario, in un campo magnetico B prodotto da
un filo uniforme percorso da una corrente di 10A, che giace nel piano del disco ed è orientato come la tangente al disco,
distando 20cm dal centro di quest'ultimo. Qual è la forza elettromotrice indotta tra la periferia del disco prossima al filo ed il
suo centro? (vd figura)
R=10cm
d=20cm
I=10A
Fem?
Soluzione: Il problema è simile al problema 5 posto nell'appello di Luglio 2008, con la sola differenza che occorre valutare
il campo magnetico prodotto dal filo con la legge di Biot-Savart. Un modo semplice di procedere è utilizzare la forza di
Lorentz come fatto nella lezione 11: un carica libera del conduttore ad una distanza r dal centro ruota con velocità
v(r ) = ω r = 2πf r La frequenza f è il numero di rivoluzioni al secondo, cioè 20 nel nostro caso. La forza per unità di
carica, essendo la velocità di rotazione perpendicolare al campo stesso, è semplicemente vB. Questa deve essere integrata
lungo il percorso tra centro ed estremo della circonferenza per avere la fem richiesta. Il campo magnetico B, considerando il
centro dei cerchio come origine, ha come modulo (tutto orientato ortogonale al disco)
B(r ) =
d R
; fem = ∫ v(r ) B (r )dr = fµId ln
− = 9.7 µV
2π (d − r )
d −R d
0
µI
R












