Simulazione di circuito risonante RLC con SPICE e confronto con

Università degli Studi di Bologna
Seconda Facoltà di Ingegneria - Sede di Cesena
C.d.L. in Ingegneria Elettronica e delle Telecomunicazioni
Simulazione di circuito risonante RLC con SPICE
e confronto con analisi tradizionale
Laboratorio di Elettronica L-A (prof. C. Fiegna)
Anno Accademico 2008/09
Data esecuzione: 27 aprile 2009
Marco
Alessandrini
Alessandro
Callozzo
Lorenzo
Minghini
0000281742
[email protected]
0000286147
[email protected]
0000274090
[email protected]
Sommario
È fornito un circuito risonante RLC, pilotato in corrente, che si comporta
in frequenza come filtro di tipo passa-banda. Dopo un’analisi dell’impedenza
dal punto di vista analitico-algebrico, il filtro sarà implementato col software
SPICE per valutare qualitativamente la caratteristica (in frequenza) di impedenza del filtro e la rispondenza tra i calcoli teorici e la simulazione. Inoltre, oggetto di analisi specifica sarà anche il transitorio iniziale del filtro e il
comportamento nel dominio del tempo, quando stimolato da un opportuno
segnale.
Entrambe le simulazioni, in frequenza e in transitorio, saranno effettuate sia con induttore ideale, sia con induttore reale, quindi dotato di resistenza serie. In tali condizioni si valuteranno gli effetti della resistenza sulle caratteristiche del filtro, compresa la velocità di risposta al transitorio di
accensione.
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Indice
1 Dati di ingresso
2
2 Quesiti generali
3
3 Quesiti analitici
4
4 Analisi in frequenza
4.1 Analisi preliminare in frequenza . . . . . . . . . . . . . . . . . . . . .
4.2 Analisi in frequenza con R1 = 0 Ω . . . . . . . . . . . . . . . . . . . .
4.3 Analisi in frequenza con R1 = 66, 2 Ω . . . . . . . . . . . . . . . . . .
5
5
6
9
5 Analisi in transitorio
5.1 Analisi in transitorio con R1 = 0 Ω . . . . . . . . . . . . . . . . . . .
5.2 Analisi in transitorio con R1 = 66, 2 Ω . . . . . . . . . . . . . . . . .
11
11
13
Elenco delle figure
16
1
Dati di ingresso
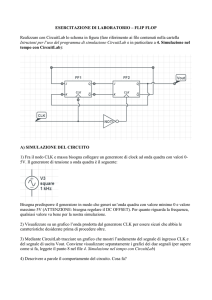
Il circuito in analisi è in figura 1.
Figura 1: Bipolo RLC, pilotato in corrente
Parametri.
• L1 = 10 mH
• R2 = 6 kΩ
• fm = 10 kHz
Metodo analitico. Il circuito è simulato con il software P-SPICE, parte costitutiva dell’ambiente di sviluppo OrCAD. Grazie ad esso si implementano le netlist
del circuito, potendo analizzare i grafici delle simulazioni plottando le grandezze
d’interesse ed effettuando le misure più opportune.
Indice
2
2
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Quesiti generali
1) Quale tipo di simulazione si deve effettuare per ottenere una analisi in
frequenza del circuito? Per analizzare in frequenza il circuito bisogna effettuare
una simulazione di tipo .AC, in particolare per una investigazione di massima si può
impostare la simulazione come segue:
.AC DEC 100 10 100000
cioè si esamina il circuito tra la frequenza 10 Hz e la frequenza 100.000 Hz = 100 kHz,
riportando l’analisi su ascissa logaritmica e rilevando 100 punti per ogni decade.
2) Quale tipo di simulazione si deve effettuare per ottenere la risposta del
circuito ad un ingresso nullo per t < 0 e sinusoidale per t ≥ 0? Per rilevare
la risposta del circuito, inizialmente inattivo, ad uno stimolo sinusoidale fornito
dopo un convenzionale t = 0 si utilizza una simulazione del transitorio (.TRAN).
Ricordando che la sintassi è:
.TRAN <Tstep> <Tstop> [<Tstart> [<Tmax>]]
con:
• Tstep: passo temporale con cui il simulatore emette i risultati della simulazione;
• Tstop: tempo finale di simulazione;
• Tstart: tempo iniziale di simulazione (o, meglio, di emissione dei dati);
• Tmax: limite superiore del passo temporale di integrazione, impiegato dal
solutore numerico di Spice (minore di Tstep),
si può esaminare il circuito da t = 0 per i successivi 2 s = 2000 ms, con passo di
5 ms, con il comando:
.TRAN 5m 2
2 Quesiti generali
3
3
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Quesiti analitici
3) Determinare le espressioni simboliche dell’impedenza Z(s) = V (s)/I(s),
dei suoi zeri e dei suoi poli. L’espressione simbolica di Z(s) si calcola come
segue:
Z(s) =
V (s)
I(s)
=
R2 +
=
R2 +
(R1 + sL1 ) · sC1 1
R1 + sL1 +
1
sC1
R1 +sL1
sC1
s2 L1 C1 +sR1 C1 +1
sC1
R1 + sL1
1 + sR1 C1 + s2 L1 C1
s2 L1 C1 R2 + s(L1 + R1 R2 C1 ) + (R1 + R2 )
=
1 + sR1 C1 + s2 L1 C1
1 R2
1 R2 C1
+ s2 LR11C+R
1 + s L1 +R
R1 +R2
2
= (R1 + R2 )
1 + sR1 C1 + s2 L1 C1
=
R2 +
Gli zeri di Z(s) sono:
z1,2
s2 L1 C1 R2 + s(L1 + R1 R2 C1 ) + (R1 + R2 ) = 0
p
−(L1 + R1 R2 C1 ) ± (L1 + R1 R2 C1 )2 − 4(R1 + R2 )L1 C1 R2
=
2L1 C1 R2
I poli di Z(s) sono:
p1,2
s2 L1 C1 + sR1 C1 + 1 = 0
p
−R1 C1 ± (R1 C1 )2 − 4L1 C1
=
2L1 C1
4) Ipotizzando L1 = 10 mH, R2 = 6000 Ω, R1 = 0 Ω, determinare il valore di
C1 affinché la frequenza di risonanza sia fm = 10 kHz.
fm =
1
√
2π L1 C1
⇒
C1 =
1
= 25, 3 nF
2L
4π 2 fm
1
5) In base ai valori di L1 , R1 , R2 e C1 determinare il valore teorico
dell’impedenza Z(f ) per f = fm = 10 kHz. Trascurando il transitorio:
σ=0
s = σ + jω = j2πf = s(f )
Con i valori assegnati e, in particolare, R1 = 0 Ω, si ottiene sostituendo nella
espressione generale di Z(f ):
Z(s)
= R2
Z(ω)
=
R2
Z(f )
=
R2
Z(fm )
da cui:
L1
+ s2 L1 C1
1 + sR
2
1 + s2 L1 C1
L1
1 + jω R
− ω 2 L1 C1
2
1 − ω 2 L1 C1
L1
1 + j2πf R
− 4π 2 f 2 L1 C1
2
1 − 4π 2 f 2 L1 C1
= (6 + j523, 599) kΩ
Z(fm ) = 523, 633 kΩ
3 Quesiti analitici
,
arg Z(fm ) = 89, 34◦
4
=
$
CC
BY:
4
\
Simulazione di circuito risonante RLC con SPICE
Analisi in frequenza
L’analisi in frequenza è svolta alimentando il circuito con un generatore di corrente
con componente AC pari a 0, 5 mA e componente DC pari a 1 mA:
I(t) = 1 + 0, 5 sin(ωt) mA
Si svolge l’analisi in due situazioni, variando il valore di R1 .
4.1
Analisi preliminare in frequenza
Analizzando Z(s) si nota che presenta due zeri e due poli, entrambe le coppie
sono complesse coniugate. Si procede con lo studio di zeri e poli, singolarmente,
per ricavare il coefficiente di smorzamento δ e la pulsazione di risonanza ωn . In
particolare, utilizziamo la funzione:
Z(s) = (R1 + R2 )
1 R2 C1
1 R2
+ s2 LR11C+R
1 + s L1 +R
R1 +R2
2
1 + sR1 C1 + s2 L1 C1
che, sostituendo s = jω, diventa:
Z(ω) = (R1 + R2 )
1 R2 C1
1 R2
1 + jω L1 +R
− ω 2 LR11C+R
R1 +R2
2
1 + jωR1 C1 − ω 2 L1 C1
• Si nota il guadagno statico K = R1 + R2 , che sarà presente dalle minime
frequenze fino al primo zero o polo che si presenta nella fdt, e poi di nuovo
dopo che entrambi zeri e poli hanno manifestato le proprie caratteristiche. Una
conferma della situazione è visibile sul plot di Z(f ) nelle successive figure 3
(K = 6000 Ω) e 5 (K = 6066, 2 Ω).
• Nel caso con R1 = 0 Ω si trova, per gli zeri:
1 + jδ
(
2δ
ωn
1
2
ωn
ω
ω2
− 2 = 1 + jω · 1, 67 · 10−6 − 25, 3 · 10−11 ω 2
ωn
ωn
= 1, 67 · 10−6
= 25, 3 · 10−11
;
δ = 0, 052
ωn = 62869, 5
⇒
fn = 10006 Hz
mentre per i poli:
1 + jδ
(
2δ
ωn
1
2
ωn
=0
= 25, 3 · 10−11
ω
ω2
− 2 = 1 − 25, 3 · 10−11 ω 2
ωn
ωn
;
δ=0
ωn = 62869, 5
⇒
fn = 10006 Hz
A ωn = 10 kHz è presente il contributo dei poli c.c. e degli zeri c.c.: ciascuna coppia introduce nella funzione di trasferimento una pendenza (i poli
di −40 dB/ dec, gli zeri di +40 dB/ dec), col risultato che le due coppie si
annullano vicendevolmente. Da questa situazione rimane un picco, che diverge perché entrambe le coppie lo presentano alla stessa frequenza (ωn ) con
parametri nulli o quasi di δ (δ = 0 nei poli, δ = 0, 052 ' 0 negli zeri).
• Se si approssima, come fatto in SPICE, R1 = 0, 000001 Ω si ottengono risultati
assolutamente comparabili per gli zeri:
1 + jδ
(
2δ
ωn
1
2
ωn
ω
ω2
− 2 = 1 + jω · 1, 67 · 10−6 − 25, 3 · 10−11 ω 2
ωn
ωn
= 1, 67 · 10−6
= 25, 3 · 10−11
4 Analisi in frequenza
;
δ = 0, 052
ωn = 62869, 5
⇒
fn = 10006 Hz
5
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Lo stesso vale anche per i poli:
ω
ω2
− 2 = 1 + jω · 25, 3 · 10−15 − 25, 3 · 10−11 ω 2
ωn
ωn
1 + jδ
(
2δ
ωn
1
2
ωn
= 25, 3 · 10−15
= 25, 3 · 10−11
;
δ = 7, 95 · 10−10 ' 0
ωn = 62869, 5 ⇒ fn = 10006 Hz
Tali risultati giustificano l’approssimazione operata nella simulazione di SPICE.
• Nel caso con R1 = 66, 2 Ω si trova, per gli zeri:
1 + jδ
(
2δ
ωn
1
2
ωn
ω2
ω
− 2 = 1 + jω · 3, 305 · 10−6 − 25, 024 · 10−11 ω 2
ωn
ωn
= 3, 305 · 10−6
= 25, 025 · 10−11
;
δ = 0, 1045
ωn = 63215, 2
⇒
fn = 10061 Hz
mentre per i poli:
1 + jδ
(
2δ
ωn
1
2
ωn
ω2
ω
− 2 = 1 + jω · 1, 675 · 10−6 − 25, 3 · 10−11 ω 2
ωn
ωn
= 1, 675 · 10−6
= 25, 3 · 10−11
;
δ = 0, 053
ωn = 62869, 5
⇒
fn = 10006 Hz
A ωn = 10 kHz è presente il contributo dei poli c.c. e degli zeri c.c.: ciascuna
coppia introduce la propria pendenza con relativo picco, che non diverge perché δ non è nullo (δ = 0, 053 ' 0 nei poli, ma δ = 0, 1045 negli zeri). Poiché
poli e zeri hanno la medesima ωn , si localizza un picco di risonanza in sua
corrispondenza.
4.2
Analisi in frequenza con R1 = 0 Ω
Per simulare il circuito con analisi in frequenza è stata utilizzata la seguente netlist
di SPICE (che realizza il circuito coi nodi indicati in figura 2):
* RLC PARALLELO - ANALISI IN FREQUENZA
* 27 aprile 2009
* R1=0
; (gen. di corrente: DC 1 milliampere, ampiezza AC 0.5 milliampere)
I1 1 0 AC=0.5M DC=1M
; (resistore da 0 ohm)
R1 3 0 0.00001
; (resistore da 6000 ohm)
R2 1 2 6000
; (induttore da 10 millihenry)
L1 2 3 0.01
; (induttore da 25.3 nanofarad)
C1 2 0 25.3N
; ANALISI IN FREQUENZA DA 10Hz a 100kHz (1000 campioni per decade)
.AC DEC 1000 10 100000
.PROBE V(1), I(R2)
.END
In particolare, si può notare che vengono memorizzate da PROBE la tensione
V (1) = V (t) (tensione del nodo 1) e la corrente I(R2) = I(t) (corrente su R2 ,
quindi sul generatore I). Inoltre, R1 non è posto a 0 come richiesto, viceversa
SPICE genera un errore a causa del quale non compila: per questo, in alternativa,
è stato inserito un valore trascurabile, pari a 10−5 , che l’analisi in frequenza prima
effettuata ha dimostrato compatibile con la situazione.
4.2 Analisi in frequenza con R1 = 0 Ω
6
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Figura 2: Bipolo RLC, pilotato in corrente, come da netlist SPICE
6) Si generino tre grafici distinti all’interno della stessa schermata: ampiezza della tensione V (f ), ampiezza della corrente I(f ), modulo dell’impedenza Z(f ) = V (f )/I(f ). Si visualizzino i grafici sia in scala lineare
che in scala logaritmica. I grafici (dall’alto in basso) di V (f ), I(f ), |Z(f )|
e arg(Z(f )) sono in figura 3 con scala logaritmica dell’asse delle frequenze, e in
figura 4 con scala lineare dell’asse delle frequenze.
* RLC PARALLELO - ANALISI IN FREQUENZA
Date/Time run: 05/01/09 17:27:07
Temperature: 27.0
(A) de.dat (active)
50V
40V
30V
20V
10V
0V
V(1)
1.0mA
0.5mA
0A
I(R2)
100K
0
ABS(V(1)/I(R2))
90d
0d
SEL>>
-90d
5.0KHz
6.0KHz
P(V(1)/I(R2))
7.0KHz
8.0KHz
9.0KHz
10KHz
11KHz
Frequency
Page 1
Date: May 01, 2009
20KHz
Time: 17:28:04
Figura 3: Simulazione .AC con R1 = 0 Ω
7) Qual è il valore della frequenza di risonanza fm del circuito? Corrisponde al valore teorico? Con gli strumenti di analisi dei plot, presenti in
SPICE, si è rilevato il massimo picco di tensione in corrispondenza della frequenza
fm = 10, 012 kHz. Con ottima approssimazione, doverosa a causa della non nullità
di R1 come ipotizzato, la frequenza rilevata corrisponde al valore teorico atteso,
pari a 10 kHz.
Alla frequenza di risonanza si sono registrati i valori:
• V (1) = 284, 278 V;
• I(R2) = 0, 5 mA.
4.2 Analisi in frequenza con R1 = 0 Ω
7
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
* RLC PARALLELO - ANALISI IN FREQUENZA
Date/Time run: 05/01/09 17:27:07
Temperature: 27.0
(A) de.dat (active)
50V
40V
30V
20V
10V
0V
V(1)
1.0mA
0.5mA
0A
I(R2)
100K
0
ABS(V(1)/I(R2))
90d
0d
SEL>>
-90d
5KHz
10KHz
20KHz
P(V(1)/I(R2))
Frequency
Page 1
Date: May 01, 2009
Time: 17:28:48
Figura 4: Simulazione .AC con R1 = 0 Ω (scala lineare)
Da questi valori si può calcolare il modulo teorico dell’impedenza alla fm , pari a
V (1)
= 568, 556 kΩ.
I(R2)
8) Qual è il valore del modulo dell’impedenza Z(fm )? Differisce da quella
teorica? Se sı̀, perché? Alla frequenza
di risonanza si è registrato un valore del
1
modulo dell’impedenza pari a Z(fm ) = 568, 557 kΩ. L’errore commesso è pari a:
∆|Z(fm )| = |568, 557 − 525, 102| = 43, 455 kΩ
corrispondente a poco più dell’8% di quanto previsto. Tale scostamento può essere
in parte attribuito alla non nullità di R1 , come ipotizzato in teoria.
9) Generare il diagramma delle fasi relativo all’impedenza Z(f ) del bipolo. Il diagramma delle fasi è presente nelle figure 3 e 4.
10) Qual è il valore della fase dell’impedenza Z(fm )? Differisce da quella
teorica? Se sı̀, perché? Alla frequenza
si è registrato un valore
di risonanza
2
dell’argomento dell’impedenza pari a arg Z(fm ) = −89, 395◦ . A meno del segno,
l’errore commesso è nullo: ciò è dovuto alla simmetria centrale del diagramma della
fase rispetto alla frequenza di risonanza, a causa della quale un modesto incremento
di f rispetto a fm è tale da avere fase negativa (come in questo caso), mentre un lieve
decremento di f provoca una fase positiva (come nel caso teorico). Poiché R1 = 0,
nell’intorno della frequenza fm la fase assume un comportamento asintotico poiché
varia pressoché verticalmente da +90◦ a −90◦ in un ridottissimo range di frequenza.
1 Il
2 Il
plot è stato ottenuto con il comando ABS(V(1)/I(R2)).
plot è stato ottenuto con il comando P(V(1)/I(R2)).
4.2 Analisi in frequenza con R1 = 0 Ω
8
4.3
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Analisi in frequenza con R1 = 66, 2 Ω
Con i valori assegnati e, in particolare, R1 = 66, 2 Ω, si ottiene sostituendo nella
espressione generale di Z(f ):
R1 sL1
s2 L1 C1 + sC1 R1 + 1
R1 + j2πf L1
Z(f ) = R2 +
1 + j2πf C1 R1 + (j2πf )2 L1 C1
Z(fm ) = (11, 99 − j0, 562) kΩ
Z(s)
da cui:
= R2 +
Z(fm ) = 12, 0032 kΩ
arg Z(fm ) = −2, 68◦
,
6bis) Si generino tre grafici distinti all’interno della stessa schermata:
ampiezza della tensione V (f ), ampiezza della corrente I(f ), modulo dell’impedenza Z(f ) = V (f )/I(f ). Si visualizzino i grafici sia in scala lineare
che in scala logaritmica. I grafici (dall’alto in basso) di V (f ), I(f ), |Z(f )| e
arg(Z(f )) sono in figura 5 con scala logaritmica dell’asse delle frequenze.
* RLC PARALLELO - ANALISI IN FREQUENZA
Date/Time run: 05/01/09 17:31:46
Temperature: 27.0
(A) de.dat (active)
10V
5V
0V
V(1)
1.0mA
0.5mA
0A
I(R2)
15K
10K
5K
0
ABS(V(1)/I(R2))
45d
0d
SEL>>
-45d
5.0KHz
6.0KHz
P(V(1)/I(R2))
7.0KHz
8.0KHz
9.0KHz
10KHz
11KHz
Frequency
Page 1
Date: May 01, 2009
20KHz
Time: 17:33:52
Figura 5: Simulazione .AC con R1 = 66, 2 Ω
7bis) Qual è il valore della frequenza di risonanza fm del circuito? Corrisponde al valore teorico? Con gli strumenti di analisi dei plot, presenti in
SPICE, si è rilevato il massimo picco di tensione in corrispondenza della frequenza
fm = 9, 989 kHz. Con ottima approssimazione la frequenza rilevata corrisponde al
valore teorico atteso, pari a 10 kHz.
Alla frequenza di risonanza si sono registrati i valori:
• V (1) = 5, 9964 V;
• I(R1) = 0, 5 mA.
Da questi valori si può calcolare il modulo teorico dell’impedenza alla fm , pari a
V (1)
= 11, 9928 kΩ.
I(R1)
4.3 Analisi in frequenza con R1 = 66, 2 Ω
9
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
8bis) Qual è il valore del modulo dell’impedenza Z(fm )? Differisce da
quella teorica? Se sı̀, perché? Alla frequenza
di risonanza si è registrato un
3
valore del modulo dell’impedenza pari a Z(fm ) = 11, 993 kΩ.
9bis) Generare il diagramma delle fasi relativo all’impedenza Z(f ) del
bipolo. Il diagramma delle fasi è presente nella figura 5.
10bis) Qual è il valore della fase dell’impedenza Z(fm )? Differisce da
quella teorica? Se sı̀, perché? Alla frequenza
si è registrato un
di risonanza
valore dell’argomento4 dell’impedenza pari a arg Z(fm ) = −2, 06◦ . Poiché l’errore commesso è di poco superiore al mezzo grado, si può affermare con buona
approssimazione che il valore simulato coincide con quello teorico.
3 Il
4 Il
plot è stato ottenuto con il comando ABS(V(1)/I(R2)).
plot è stato ottenuto con il comando P(V(1)/I(R2)).
4.3 Analisi in frequenza con R1 = 66, 2 Ω
10
5
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Analisi in transitorio
L’analisi in transitorio è svolta alimentando il circuito con un segnale di corrente in
ingresso pari a:
I(t) = 0, 5 sin(2πfm t) mA
Si svolge l’analisi in due situazioni, variando il valore di R1 .
5.1
Analisi in transitorio con R1 = 0 Ω
* RLC PARALLELO - ANALISI IN TRANSITORIO
* 27 aprile 2009
* R1=0
; (gen. di corrente: ampiezza AC 0.5 milliampere,
; transitorio sinusoidale a frequenza di risonanza)
I1 1 0 sin(0 0.5m 10k 0) AC=0.5m
; (resistore da 0 ohm)
R1 3 0 0.00001
; (resistore da 6000 ohm)
R2 1 2 6000
; (induttore da 10 millihenry)
L1 2 3 0.01
; (induttore da 25.3 nanofarad)
C1 2 0 25.3N
; ANALISI IN TRANSITORIO PER 10ms (PASSO 1us)
.TRAN 1u 10m
.PROBE V(1), I(R2)
.END
11) Si generino due grafici distinti all’interno della stessa schermata;
tensione V (t), corrente I(t). I grafici (dall’alto in basso) di V (t) e I(t) sono in
figura 6. Un dettaglio degli stessi grafici è in figura 7.
* RLC PARALLELO - ANALISI IN TRANSITORIO
Date/Time run: 05/06/09 10:21:43
Temperature: 27.0
(A) RLC_TRAN.dat (active)
10V
8V
6V
4V
2V
0V
-2V
-4V
-6V
-8V
-10V
V(1)
1.0mA
0.5mA
0A
-0.5mA
SEL>>
-1.0mA
0s
1.0ms
2.0ms
3.0ms
4.0ms
5.0ms
I(R2)
Date: May 06, 2009
Time
Page 1
Time: 10:23:04
Figura 6: Simulazione .TRAN con R1 = 0 Ω
5 Analisi in transitorio
11
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
* RLC PARALLELO - ANALISI IN TRANSITORIO
Date/Time run: 05/06/09 10:21:43
Temperature: 27.0
(A) RLC_TRAN.dat (active)
10V
8V
6V
4V
2V
0V
-2V
-4V
-6V
-8V
-10V
V(1)
1.0mA
0.5mA
0A
-0.5mA
SEL>>
-1.0mA
0s
1.0ms
2.0ms
3.0ms
I(R2)
Time
Page 1
Date: May 06, 2009
Time: 10:24:11
Figura 7: Simulazione .TRAN con R1 = 0 Ω (dettaglio)
12) In quanto tempo si estingue il transitorio? Consideriamo estinto il transitorio al raggiungimento del 90% dell’ampiezza del segnale in considerazione (V (t)).
A tal fine è stato rilevato:
V (1)M AX = 6, 8967 V
per t = 684 µs
⇒ V (1)H = 90% · V (1)M AX = 6, 207 V
La forma d’onda del segnale, però, è caratterizzata da una oscillazione secondaria
che affligge la tensione, già per sua natura sinusoidale: l’effetto è noto, trattandosi
di un circuito risonante che lavora alla frequenza di risonanza. La più diretta conseguenza di questa situazione è l’instabilità del circuito, che modula in ampiezza la
tensione ai suoi capi producendo dei battimenti di periodo misurato T = 2, 11 ms,
equivalente a una frequenza f = 473, 9 Hz.
Secondariamente, non è possibile determinare la durata del transitorio, perché di
fatto questi non cessa mai: data la natura dell’uscita, non ha molto senso stabilirne
le caratteristiche.
13) Quanto vale l’ampiezza della V (t) a regime? È coerente con quella ottenuta mediante l’analisi in frequenza? Riprendendo un concetto già
espresso, si può pensare V (t) come un modulato AM, commettendo un’approssimazione che non incide sull’analisi generale. Il segnale modulante è evidentemente
periodico (praticamente sinusoidale) e, per l’analisi matematica, non assume limite
a regime, cioè per t → ∞. Ciò contrasta dal punto di vista analitico con il risultato
dell’analisi in frequenza, secondo la quale il limite assunto è molto chiaro e pari a
+∞ (5 ). Elettricamente, però, i risultati hanno pari valore logico, perché una divergenza equivale ad una instabilità, la quale porta alla non assunzione di un preciso
valore (finito o infinito che sia) nel tempo.
5 In realtà, come riportato, il valore massimo registrato in AC è V (1) = 284, 278 V. Il limite
non è quindi infinito, ma assume un preciso valore. Questa non idealità è causata dal valore molto
basso, ma non nullo come richiesto, di R1 : viceversa, SPICE non realizza l’analisi proprio perché
essa diverge, causando V (1) → +∞.
5.1 Analisi in transitorio con R1 = 0 Ω
12
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
14) Quanto vale lo sfasamento tra I(t) e V (t) a regime? È coerente con
quella ottenuta mediante l’analisi in frequenza? Secondo l’analisi in frequenza, lo sfasamento atteso per f = fm è nullo. Nell’intorno di fm , però, la fase si
comporta in maniera asintotica, proponendo forti variazioni di fase a fronte di minime variazioni di frequenza: sarebbero sufficienti minime tolleranze nei componenti
o nel circuito oggetto di simulazione per evidenziare sfasamenti lontani dal teorico.
Dall’analisi del transitorio si rileva con discreta precisione che V (1) e I(R1) sono
in fase, poiché visivamente le creste delle forme d’onda si susseguono nel tempo
senza ritardo. A una prima impressione, quindi, le due analisi producono lo stesso
risultato.
Volendo misurare con precisione il massimo di due creste corrispondenti delle
due grandezze, per verificare che si presentassero allo stesso istante, è stato rilevato:
tV (1)P = 684, 071 µs
tI(R1)P = 771, 780 µs
il che significa che la corrente è in ritardo sulla tensione di 87, 709 µs. Visto che alla
frequenza di risonanza data il periodo è T = 100 µs, lo sfasamento è:
100 µs
:
360◦
=
87, 709 µs
:
x◦
x◦ ' 315, 7524◦ = −44◦
Tale risultato, però, è fortemente condizionato dalle forti approssimazioni operate
da SPICE, che nonostante un numero elevatissimo di campioni per unità di tempo6
produce dei grafici poco dettagliati e in cui le forme d’onda, benché teoricamente
sinusoidali, si riducono a delle onde spezzate private delle creste. Ciò pare aver
determinato un errore nel rilievo dei tempi di cresta, e di conseguenza un erronea
valutazione dello sfasamento.
5.2
Analisi in transitorio con R1 = 66, 2 Ω
11bis) Si generino due grafici distinti all’interno della stessa schermata;
tensione V (t), corrente I(t). I grafici (dall’alto in basso) di V (t) e I(t) sono in
figura 8.
12bis) In quanto tempo si estingue il transitorio? Consideriamo estinto il
transitorio al raggiungimento del 90% dell’ampiezza del segnale in considerazione
(V (t)). A tal fine è stato rilevato a regime:
V (1)M AX = 4, 6553 V
per t = 1, 38 ms
⇒ V (1)H = 90% · V (1)M AX = 4, 190 V
Scandagliando la forma d’onda del segnale, è stato apprezzato il superamento della
soglia V (1)H in corrispondenza del tempo t = 272, 2 µs, che è quindi il tempo
necessario ad estinguere il transitorio.
13bis) Quanto vale l’ampiezza della V (t) a regime? È coerente con
quella ottenuta mediante l’analisi in frequenza? Secondo quanto rilevato
in precedenza, alla frequenza di risonanza ci si aspetta un’ampiezza in tensione
V (1) = 5, 9964 V. Misurando l’ampiezza di una cresta in istanti diversi successivi
al termine del transitorio, non è mai stato rilevato un valore simile, ma sempre
inferiore ai 5 V.
In figura 9 è stata riportata la schermata della simulazione realizzata con un
differente compilatore SPICE (LT-SPICE). In essa sono visualizzati l’analisi in frequenza (in alto a sinistra) e l’analisi del transitorio (in basso a sinistra), entrambe
6 Anche ponendo l’intervallo di campionamento a 1 ns o inferiore la situazione non è mai
cambiata.
5.2 Analisi in transitorio con R1 = 66, 2 Ω
13
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
* RLC PARALLELO - ANALISI IN TRANSITORIO
Date/Time run: 05/06/09 10:09:01
Temperature: 27.0
(A) RLC_TRAN.dat (active)
10V
8V
6V
4V
2V
0V
-2V
-4V
-6V
-8V
-10V
V(1)
1.0mA
0.5mA
0A
-0.5mA
SEL>>
-1.0mA
0s
0.5ms
1.0ms
I(R2)
Date: May 06, 2009
Time
Page 1
Time: 10:20:42
Figura 8: Simulazione .TRAN con R1 = 66, 2 Ω
coincidono con quanto risultato fin’ora con la differenza che in LT-SPICE entrambe
le analisi ottengono la medesima ampiezza alla frequenza fm , e cioè V (1) = 6 V.
Questo riscontro, sempre ottenuto in ambiente SPICE, conforta una risposta positiva al quesito posto; d’altro canto, solleva un’osservazione relativa alla qualità
dell’analisi grafica di P-SPICE rispetto ai software concorrenti, che ha condizionato
buona parte dell’analisi dei transitori. Una spiegazione che è stata ipotizzata, riguardo alla discordanza di dati ottenuti con P-SPICE, è legata al taglio delle creste
operato nonostante il campionamento spinto alla ricerca del massimo dettaglio: probabilmente, aggiungendo l’ampiezza delle creste alle misure inferiori ai 5 V registrati
si sarebbero ottenuti i 5, 9964 V attesi.
14bis) Quanto vale lo sfasamento tra I(t) e V (t) a regime? È coerente con
quella ottenuta mediante l’analisi in frequenza? In maniera perfettamente
simile al caso con R1 = 0 Ω, l’analisi in frequenza predice uno sfasamento nullo
atteso a f = fm . Analizzando il transitorio il rilievo ha prodotto le stesse risultanze
del caso analogo: V (1) e I(R1) sembrano visivamente in fase, ma non è possibile
confermare numericamente la stima con misure certe a causa del poco dettaglio
della forma d’onda di V (1).
5.2 Analisi in transitorio con R1 = 66, 2 Ω
14
=
$
CC
BY:
Figura 9: Simulazione .TRAN e .AC con R1 = 66, 2 Ω, realizzata con LT-SPICE
\
Simulazione di circuito risonante RLC con SPICE
5.2 Analisi in transitorio con R1 = 66, 2 Ω
15
=
$
CC
BY:
\
Simulazione di circuito risonante RLC con SPICE
Elenco delle figure
1
2
3
4
5
6
7
8
9
Bipolo RLC, pilotato in corrente . . . . . . . . . . . . . . . . . . . .
Bipolo RLC, pilotato in corrente, come da netlist SPICE . . . . . .
Simulazione .AC con R1 = 0 Ω . . . . . . . . . . . . . . . . . . . . . .
Simulazione .AC con R1 = 0 Ω (scala lineare) . . . . . . . . . . . . .
Simulazione .AC con R1 = 66, 2 Ω . . . . . . . . . . . . . . . . . . . .
Simulazione .TRAN con R1 = 0 Ω . . . . . . . . . . . . . . . . . . . .
Simulazione .TRAN con R1 = 0 Ω (dettaglio) . . . . . . . . . . . . . .
Simulazione .TRAN con R1 = 66, 2 Ω . . . . . . . . . . . . . . . . . .
Simulazione .TRAN e .AC con R1 = 66, 2 Ω, realizzata con LT-SPICE
2
7
7
8
9
11
12
14
15
\
=
$
CC
BY:
Quest’opera è stata rilasciata sotto la licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 2.5 Italia. Per leggere
una copia della licenza visita il sito web
http://creativecommons.org/licenses/by-nc-nd/2.5/it/
o spedisci una lettera a Creative Commons, 171 Second Street, Suite
300, San Francisco, California, 94105, USA.
È consentito riprodurre e distribuire liberamente il presente testo, senza apporvi
modifiche e mantenendo sempre riconoscibile il nome degli autori, purché non a scopo di lucro, senza scopi commerciali (direttamente o indirettamente) e per esclusivo
uso personale.
È possibile pubblicare il file o sue parti su siti internet, purché siano citati in
maniera evidente gli autori (Marco Alessandrini, Alessandro Callozzo e Lorenzo
Minghini).
Per qualunque informazione, problematica, suggerimento o reclamo utilizzare
l’indirizzo [email protected].
Elenco delle figure
16