ESERCITAZIONI SU DOMANDA, OFFERTA E MERCATO
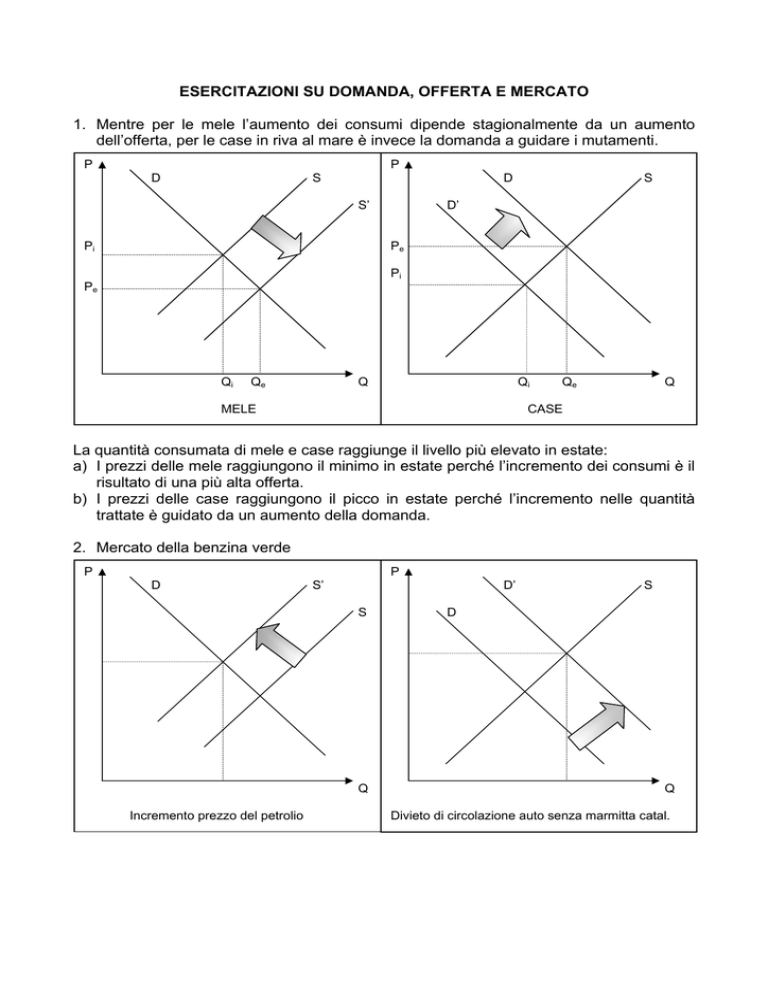
1. Mentre per le mele l’aumento dei consumi dipende stagionalmente da un aumento
dell’offerta, per le case in riva al mare è invece la domanda a guidare i mutamenti.
P
P
D
S
D
S’
Pi
S
D’
Pe
Pi
Pe
Qi
Qe
Qi
Q
MELE
Qe
Q
CASE
La quantità consumata di mele e case raggiunge il livello più elevato in estate:
a) I prezzi delle mele raggiungono il minimo in estate perché l’incremento dei consumi è il
risultato di una più alta offerta.
b) I prezzi delle case raggiungono il picco in estate perché l’incremento nelle quantità
trattate è guidato da un aumento della domanda.
2. Mercato della benzina verde
P
P
D
S’
D’
S
Q
Incremento prezzo del petrolio
S
D
Q
Divieto di circolazione auto senza marmitta catal.
3. La caduta del prezzo del gasolio sposta la curva di offerta del pesce fresco verso
destra. Il rapporto scientifico sul mercurio sposta invece la curva di domanda verso
sinistra. Il prezzo di equilibrio scende (in entrambi i casi), ma la quantità di equilibrio
può salire (a) oppure scendere (b).
P
P
D
S
D
D’
S
S’
S’
D’
Q
Q
4. Poiché i fax ed i servizi di recapito veloce sono sostituti, il notevole calo del prezzo dei
fax avrà fatto diminuire la domanda dei servizi di recapito veloce da D a D’. Di
conseguenza saranno diminuiti sia il numero di recapiti veloci effettuati sia il loro
prezzo unitario, come risulta dall’intersezione tra le curve S e D’.
Dollari
S
D
D’
Numero recapiti veloci
5. Domanda inversa: Pd = 10-3Qd
Offerta inversa : Ps = 6 + Qs
a) Otteniamo i valori di equilibrio di prezzo e di quantità eguagliando D e S:
10 – 3Q = 6 + Q
Q* = 1
Il prezzo di equilibrio si ottiene sostituendo Q* indifferentemente nella curva di
offerta o nella curva di domanda:
P* = 7
P
10
S
S’
7
6
5,5
4
1 1,5
3
Q
b) Sussidio di due lire per banana ai produttori
Esprimiamo D e S in funzione dei prezzi ed otteniamo le curve di domanda e di
offerta dirette:
D(Pd) = 10/3 – 1/3Pd
S(Ps) = Ps –6
Se il governo paga un sussidio di 5 lire sulla quantità prodotta ossia i produttori
ricevono 5 lire per quantità prodotta, il prezzo effettivamente ricevuto dai
produttori e rilevante per le loro decisioni di produzione, diventa di 5 lire superiore
a quello pagato dai consumatori
Ps = Pd + 2
Per ottenere quantità e prezzi di equilibrio dopo il sussidio dobbiamo risolvere
l’equazione
D(Pd) = S(Ps) sostituendo abbiamo
10/3 – 1/3Pd = Pd +2 – 6
10/3 + 4 = 1/3Pd + Pd
10 + 12 = Pd + 3 Pd
Pd* = 22/4 = 5,5
Ps* = Pd* + 2 = 5,5 + 2 = 7,5
La quantità di equilibrio sarà
S(Ps) = 7,5 – 6 = 1,5 ⇒ Q* = 1,5
La spesa complessiva sarà 1,5•2=3
6. Il mercato del bene q è caratterizzato dalle seguenti funzioni (inverse) di domanda e di
offerta:
P = 30 – 1/2qD
P = 10 + 1/10qS
a) Determinare l’equilibrio di mercato e l’elasticità della domanda rispetto al prezzo nel
punto di equilibrio individuato.
Equilibrio di mercato:
D=S
30 – 1/2qD = 10 + 1/10qS con qD = qS = q*
300 – 5 q* = 100 + q*
q* = 200/6 = 100/3
p* = 30 – ½(100/3) = 30 – 50/3 =40/3
q* =100/3; p* = 40/3
Elasticità della domanda al prezzo:
dq D p
•
,p
dq q
Funzione di domanda diretta: qD = 60 – 2p
εq
=
D
dqD/ dp= -2
⎞ = −2(2 / 5) = −4 / 5
= −2⎛⎜ 40 3
100 3 ⎟⎠
⎝
b) Trovate p e q nel punto di elasticità unitaria la curva di domanda è:
qD=60-2p
dq p
ε q, p =
= −1
dp q
⎧q D = 60 − 2 p ⎫ ⎧q D = 60 − 2 p ⎫
⎪
⎪ ⎪
⎪
dq p
⎬
⎬⇒⎨ p
⎨
⎪
⎪ε q , p = dp q = −1⎪ ⎪2 q = 1
⎭
⎭ ⎩
⎩
D
⎧q = 60 − 2 p ⎫ ⎧2 p = 60 − 2 p ⎫ ⎧4 p = 60 ⎫ ⎧ p = 15⎫
⎬
⎬⇒⎨
⎬⇒⎨
⎬⇒⎨
⎨
p
q
q
=
=
2
2
(
15
)
p
q
=
2
⎭ ⎩q = 30 ⎭
⎭ ⎩
⎭ ⎩
⎩
εq
d
,p
7. La funzione di domanda lineare avrà equazione del tipo qD=-ap+b dove a e b sono
parametri incogniti che dobbiamo determinare.
Per determinarli sfruttiamo le due informazioni che abbiamo: cioè che qD(2000) = 500
e che ε q , p q D ( p = 2000 ) = −0,1 queste danno luogo al seguente sistema di equazioni
[
]
nelle incognite a e b:
⎫
⎧500 = − a 2000 + b
⎪ ⎧b = 550 ⎫
⎪
dq p
⎬
⎬⇒⎨
⎨
⎛ 2000 ⎞
⎪ε q , p = dp q = a⎜ 500 ⎟ = −0,1⎪ ⎩a = −1 / 40⎭
⎝
⎠
⎭
⎩
dq/dp se la funzione di domanda è qD=-ap+b è uguale ad a
Da esso risulta: a =-1/40, b=550
Ciò vuol dire che la funzione di domanda giornaliera di pere è: qD=-1/40p+1000
8.
Δq q
Δp p
ΔP
pertanto, se
= 0,02 allora
P
Δq q
Δq
− 0,2 =
⇒
= −0,2(0,02) = −0,004
0,02
q
Gli acquisti di cibo si ridurranno dello 0,4%
− 0,2 = ε =











