Platone
Timeo
La creazione dell’universo
Questo dialogo di Platone riprende la teoria di Pitagora sulla
formazione dell’universo, secondo la quale il dio creatore avrebbe
suddiviso l’essenza primordiale in base ad un’armonia matematica,
simile a quella che determina la consonanza delle note musicali. Il
cosmo sarebbe stato composto di tante sfere, in moto perpetuo, una
contenuta nell’altra, ad ognuna delle quali sarebbe stato attaccato un
corpo celeste. Ecco come Timeo descrive l’origine e la natura del
movimento della volta celeste rispetto alla Terra, spiegando anche
l’apparente inclinazione dell’orbita delle stelle fisse rispetto
all’equatore terrestre.
“Tutta questa composizione dunque, dopo averla scissa in due nel
senso della lunghezza, e sovrapposte le due metà rispettivamente l’una
sull’altra in forma di X;
queste egli le piegò, ognuna di per sé, in cerchio, collegandole poi
ciascuna con sé e tra sé nell’<altro> punto <del cerchio> opposto alla
loro intersezione, e impresse loro un moto di rotazione uniforme e
sempre nello stesso luogo; e dei due cerchi pose l’uno fuori e l’altro
dentro. E così il moto <del cerchio> esterno lo destinò ad essere della
natura del medesimo; l’interno, di quella dell’altro.
Medesimo
Altro
Quello poi del medesimo lo girò, secondo il lato <d’un parallelogrammo>
a destra; quello dell’altro, secondo la diagonale a sinistra; ma la
preminenza la diede alla circolazione del medesimo e dell’omogeneo;
giacché lasciò questa unica ed indivisa; ma dopo d’avere scisso quella
interna sei volte in sette cerchi disuguali giusta gli intervalli del doppio
e del triplo, tre per ciascuna parte; ordinò che i cerchi andassero gli uni
agli altri contrario; e tre <si movessero> con <velocità> eguale e gli altri
quattro con <velocità> disuguale, così tra loro come con i tre, pur
movendosi secondo rapporti costanti.”
(cit. da Platone, Tutte le opere, trad. di G. Pugliese Carratelli, Sansoni,
Firenze 1974, pag. 1106).
Medesimo
Altro
I quattro elementi e i cinque solidi platonici
Il grande matematico greco Euclide, al termine dell’ultimo libro dei
suoi Elementi, dimostra che esistono solo cinque tipi diversi di solidi
regolari, ossia solidi aventi come facce poligoni regolari congruenti.
Platone vede in questi corpi le figure fondamentali dell'universo, le
forme dei suoi costituenti primordiali. Anche Keplero, nel Seicento, li
immaginerà collocati idealmente nel cosmo, intorno ai singoli pianeti.
“Sia questo, dunque, in breve, il ragionamento <a giustificazione> del
mio parere: che c’erano e l’essere e lo spazio e la generazione, tre
termini in tre modi diversi, <esistenti> anche prima che il cielo
nascesse; e che la nutrice della generazione, essendo irrigata ed
infocata e assumendo le forme di terra e d’aria e patendo tutte le altre
passioni, che a queste conseguono; appariva a vedersi infinitamente
varia; e piena, com’era, di forze né uniformi né equilibrate, non serbava
l’equilibrio in nessuna sua parte, ma pencolando disugualmente in ogni
lato, era essa stessa scossa da loro, e, a sua volta, movendosi, le
scoteva […]. Così allora quei quattro generi <o elementi> scossi dalla
recettrice, che si moveva essa stessa a guisa d’uno strumento
scuotitore, separavano <ciascuno> da sé, quanto più potevano, le parti
più dissimili tra loro, mentre le più simili le stipavano soprattutto nel
medesimo luogo; ond’esse anche occuparono quale un posto, quale un
altro, prima che da loro l’universo ordinato nascesse […] ma quando <il
dio> prese ad ordinare l’universo, al fuoco dapprima e all’acqua e alla
terra e all’aria [….] egli dapprima dette forme e numeri. […] che fuoco e
terra e acqua e aria siano corpi, è, credo, chiaro a chicchessia; ed ogni
forma di corpo ha anche spessore. Ora, ogni spessore comprende
necessariamente la natura di superficie; e la superficie piana e
rettilinea consta di triangoli.”
È facile vedere che ogni figura poligonale è decomponibile in triangoli.
D’altra parte ogni curva può essere approssimata quanto si vuole con
una linea poligonale: basta scegliere un numero di segmenti
sufficientemente elevato.
Quindi ogni superficie piana può essere approssimata con una figura
poligonale, ottenuta dall’unione di tanti piccoli triangoli.
Poiché ogni triangolo è unione di due triangoli rettangoli,
ogni superficie può quindi essere coperta da triangoli rettangoli.
Platone prosegue osservando che:
Tutti i triangoli poi hanno principio da due <tipi di> triangoli, aventi
ciascuno un angolo retto e due acuti. E di essi l’uno, <l’isoscele>, ha da
un lato e dall’altro una parte eguale d’angolo retto diviso da lati eguali;
l’altro, <lo scaleno>, ha due parti disuguali <d’angolo retto> diviso da
due lati disuguali.
Ora, è questo il principio e del fuoco e degli altri corpi <elementari> […]
Bisogna pertanto dire quali siano quei quattro bellissimi corpi che ne
derivano, dissimili bensì tra loro, ma capaci taluni di generarsi,
dissolvendosi, gli uni dagli altri. […]
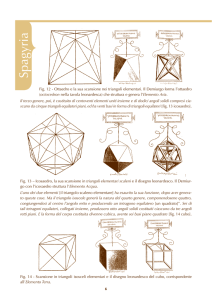
tetraedro (il fuoco)
Combinandosi […] quattro triangoli equilateri, <ciascun gruppo di> tre
angoli piani forma un angolo solido, che segue immediatamente il più
ottuso degli angoli piani. Di quattro cosiffatti <gruppi> consta la prima
specie solida, capace di dividere in parti eguali e simili tutta la
superficie della sfera <in cui è inscritta>.
ottaedro (l’aria)
La seconda poi si ha degli stessi triangoli <elementari>, riuniti però
insieme in otto triangoli equilateri, formanti un angolo solido di quattro
angoli piani; e quando si ottengano sei angoli cosiffatti, anche il
secondo corpo è così compiuto.
La terza specie poi consta di due volte sessanta triangoli elementari
uniti insieme, e di dodici angoli solidi, chiusi ciascuno da cinque
triangoli equilateri piani, ed ha venti basi <o facce> in forma di triangoli
equilateri.
icosaedro (l’acqua)
E dopo d’aver generato <questi tre solidi>, l’uno dei due elementi, <il
triangolo scaleno> ha esaurito il suo compito. Il triangolo isoscele, a sua
volta, generò la natura del quarto <corpo elementare>, componendosi
insieme quattro di questi triangoli in guisa che gli angoli retti si
congiungano nel centro e ne nasca un tetragono equilatero. Sei di tali
<tetragoni> combinati insieme formano otto angoli solidi, costituiti
ciascuno di tre angoli retti piani; sicché la forma del corpo, che ne
risulta, è cubica, con una base di sei tetragoni equilateri piani.
cubo (la terra)
Non rimaneva che una quinta combinazione, e il dio se ne servì per
<abbellire> l’universo, quando ne completò il disegno.
dodecaedro (Dio)
Platone così giustifica l’assegnazione delle forme ai vari elementi:
“Alla terra diamo la forma cubica; perché la terra è il meno mobile dei
quattro generi e il più plasmabile dei corpi, essendo necessario che tale
sia soprattutto quello de’ corpi che ha le basi più salde.
Ora, dei triangoli, supposti da principio, la base di quelli che hanno lati
eguali, è per natura più salda che non quella degli altri, che li hanno
disuguali; e delle superficie, composte dell’uno e dell’altro tipo di
triangolo, il tetragono equilatero in confronto del triangolo equilatero,
così nelle parti come nell’intero ha necessariamente una base più
stabile. Perciò, attribuendo questa figura alla terra, salviamo la
verosimiglianza del discorso; mentre invece daremo all’acqua la forma
che tra le rimanenti è la meno mobile; al fuoco, la più mobile di tutte, e
l’intermedia, all’aria; e così il corpo più piccolo, al fuoco; il più grande,
all’acqua, e l’intermedio all’aria; e il più acuto, daccapo, al fuoco; il più
grande, all’acqua, e l’intermedio, all’aria; e il più acuto, daccapo, al
fuoco; il secondo per acutezza, all’aria; il terzo, all’acqua. Di tutte
queste forme pertanto, quella che ha il minor numero di basi deve
necessariamente essere la più mobile per natura, perché è da ogni lato
la più tagliente e la più acuta;
e sarà inoltre la più leggera, perché costituita del più piccolo numero
delle stesse parti; del pari la seconda avrà le stesse caratteristiche in
grado secondario, e la terza in terzo grado. Cosicché, in conformità d’un
ragionamento retto e verosimile, la figura solida della piramide sia
elemento e seme del fuoco; la seconda per generazione diciamola
elemento e seme dell’aria; e la terza, dell’acqua. E tutti questi solidi
elementari bisogna concepirli così piccoli, che ciascuno da sé in ciascun
genere per la sua piccolezza non sia punto visibile da noi, ma allorché
molti se ne raggruppino insieme, se ne vedano le masse. E quanto ai
rapporti circa il numero e i movimenti e le altre proprietà loro, bisogna
ritenere che in quella misura, dopo che tali cose furono in ogni parte
esattamente compiute, il dio le avesse proporzionatamente e
armonicamente coordinate.”
(ibidem, pagg. 1117 - 1119)
Secondo Platone, il miscuglio degli elementi darebbe luogo ai poliedri
semiregolari, ossia poliedri le cui facce sono poligoni regolari di due o
più specie diverse. Erone riferisce che Platone ne conosceva due tipi,
mentre sappiamo che Archimede ne trovò 13.