Campo magnetico B

Lezione V
Campo magnetico B
1/15
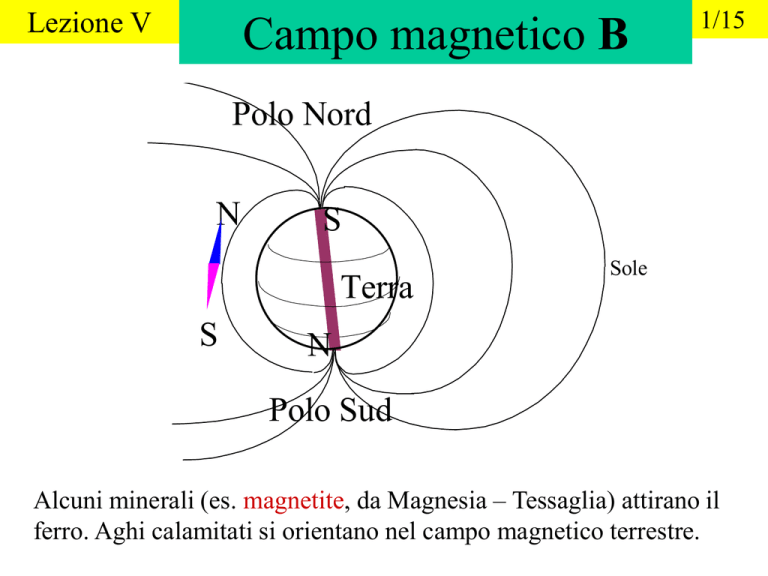
Polo Nord
N
S
Terra
S
Sole
N
Polo Sud
Alcuni minerali (es. magnetite, da Magnesia – Tessaglia) attirano il
ferro. Aghi calamitati si orientano nel campo magnetico terrestre.
Lezione V
Campo magnetico B
2/15
La Terra e le calamite sono dipoli magnetici, con proprietà simili a quelle
dei dipoli elettrici; poli opposti si attraggono e concordi si respingono; le
"linee di forza" escono dal polo nord ed entrano al sud
Il polo nord terrestre è il polo sud del dipolo magnetico terrestre
Direzione e verso di B sono indicati da un ago calamitato
Lezione V
3/15
Campo magnetico B
Lo studio quantitativo del campo magnetico B comincia a partire dal
1800 grazie alle correnti continue prodotte dalla pila di Volta.
B produce una forza f su un tratto di
conduttore l percorso da corrente I
(seconda legge di Laplace)
f  I  Δl  B
Nord
I
l
B
Il campo magnetico B
("campo di induzione magnetica” )
è l'analogo di E (campo elettrico)
in quanto è il responsabile di
azioni di forza
Sud
f
Lezione V
Campo magnetico B
4/15
forza
Dimensioni di B =
corrente  lunghezza
newton
joule  s
unità di B (SI) 


2
ampere  metro coulomb  metro
volt  s weber


 tesla(T)
2
2
metro
metro
Il weber è l’unità SI del flusso di B (teslametro2)
Per B si usa spesso il gauss = 104 tesla
Lezione V
Campo magnetico B
f
z
x
5/15
I
l
y
Sud
B
Nord
La forza è perpendicolare al piano individuato da l e B
Un osservatore orientato piedi-testa come f deve ruotare l
in senso antiorario di meno di 180° per sovrapporlo a B.
"regola della mano sinistra" = medio su l, indice su B, pollice su f
Lezione V
Campo magnetico B da I
6/15
Campo magnetico B prodotto in
P da tratto l di corrente I in O
(prima legge di Laplace chiamata
P
anche legge di Biot-Savart)
I
l
O
B
B  k m
l
Il  OP
OP
3
Per distribuzione di corrente J
J
S
B  k m
J  OP
OP
3
V con V  S  l
Lezione V
Campo magnetico B
Il valore della costante km
è legato alla scelta della
unità di corrente/carica


l
f  l   f 
7 N
km   B 
  2  10
I  I  l  I  I 
A2
La costante magnetica si
esprime solitamente
mediante la permeabilità
magnetica del vuoto 0
Il rapporto
costante elettrica /
costante magnetica
è indipendente dalla
scelta dell'unità
elettrica (carica o
corrente)
7/15
 
0
N
 0  4k m  4 10
km 
2
4
A
 N  m2 

2 
C   m2 
ke
1 4
1





 2 
k m 4 0  0  0  0  N   s 
C 2 / s 2 


7
 
 9 1016
m2
2

c
s2
c = velocità della luce
Lezione V
8/15
Campo B da spira
Campo B lungo l'asse di una spira circolare di corrente

z
y
x
dBz
dB(P)
Ids
r
r  R2  z 2
R
cos   
r
P(z)

R
R2  z2
d O
R
0 I Rd  r
dBz  dB( P)  cos  
cos  
3
4
r
0 I Rd

4 R 2  z 2
R
R z
2
2
0 IR 2

4
 R z 
2
2
3
Bz 
d

0 IR 2
2 R2  z 2
 2k m


3
R I
2
 R z 
2
2
3
Lezione V
9/15
Campo B da spira
Dalle ultime espressioni si ha:
il campo al centro della spira è inversamente proporzionale al raggio R;
a grande distanza dalla spira il campo magnetico è direttamente
proporzionale al prodotto della corrente (I) per l’area della spira
(R2) detto momento magnetico della spira di corrente

corrente  area spira  momento magnetico mmag

il momento magnetico è un vettore perpendicolare al piano della spira
e orientato con la regola della mano destra
il campo B del dipolo magnetico tende a zero con il reciproco del cubo
della distanza (come per il campo E del dipolo elettrico)
Lezione V
Spira= dipolo magnetico
10/15
Il campo al centro della spira è inversamente proporzionale al raggio R
Bz 
2

z 0

 
 0 IR 2
R z
2
2

3


 I R
  0
2z 3
z  R
2

0 I
2R
 0 mmag
2z
3
 2k m
mmag
z3
A grande distanza dalla spira il campo magnetico è inversamente proporzionale al cubo della distanza (z) dal centro della spira e direttamente
proporzionale al prodotto della corrente (I) per l’area della spira (R2).

corrente area spira  momento magnetico mmag

Dipolo elettrico e dipolo magnetico si estinguono con il reciproco del
cubo della distanza
Lezione V
dipoli elettrici e magnetici
11/15
Dipolo elettrico e dipolo magnetico sono differenti
Le linee di forza
elettriche escono
dalle cariche
positive ed entrano
in quelle negative
N
E
B
S
Manca l'equivalente di "carica" localizzata nel caso magnetico: le linee di
forza sono continue attraverso il dipolo. La divergenza di B è nulla
Lezione V
Campo B da filo di corrente
Campo in punto P a distanza R da un filo indefinito lungo z
percorso da corrente I
dz
z + dz
dzr
z
I
d
r
d
dz  R
cos 2 

O
P
R
dB(P)
P
0 I

4
 /2
O
R
0 I
B( P) 
4
R
r
cos 
z  R tan

r cos dz
 r3 

cos  d 0 I
I
 R  2R  2km R
 / 2
12/15
Lezione V
Campo magnetico B
13/15
Le linee di forza di B sono cerchi concentrici attorno al filo e vale la
"regola della mano destra"
B1/distanza
I
O
Pollice nel verso della
corrente  le dita
chiuse seguono B
l
B  l  OP
P
Lezione V
Il campo magnetico B
14/15
Forze tra fili percorsi da correnti
I1
f12
I2
0 I1I 2
 I1l1  B 2 
l1
2 r
B2
B1
l1
f21
f12
O
P
z
B2
y
r
L’ampere di corrente è stato
definito grazie alle forze su fili
x
correnti equiverse si attirano
correnti opposte si respingono
Lezione V
15/15
La divergenza di B
Le linee di B prodotte dal filo indefinito sono
anelli chiusi  B è un campo solenoidale,
ossia a divergenza nulla
Il risultato è subito dimostrabile
per fili indefiniti normali al
piano del disegno, ma è vero in
generale come conseguenza
formale della legge di Laplace.
 B  ndS  0
S
B  0
B
Qualunque siano le correnti, le linee di B sono sempre chiuse
(mancano sorgenti o pozzi di B)