Introduzione

1
Premio Cesare Bonacini 2003
Premere ed essere premuti, tirare ed essere
tirati. Esperimenti quantitativi su fenomeni
d'interazione tra corpi.
Istituto di Istruzione Superiore
“Primo Levi”, Montebelluna TV.
Studenti
GOBBO
MARTINI
SOLIGO
TRINCA
GIANPAOLO
PAOLO
MASSIMILIANO
CLAUDIO
5a A Liceo Scientifico Tecnologico
5a A Liceo Scientifico Tecnologico
5a A Liceo Scientifico Tecnologico
5a A Liceo Scientifico Tecnologico
Docenti Coordinatori
PROF.
SPADA EMANUELE
BONORA MARIO
(MATEMATICA/FISICA)
(TECNICO DI LABORATORIO)
1° Premio
Motivazione: Uno studio dell'interazione tra correnti elettriche e
magneti è stato affrontato mettendo sperimentalmente in evidenza fenomeni di cui abitualmente si legge nei libri ma che raramente sono
presentati in modo chiaramente visibile in laboratorio. Le scelte sperimentali compiute sono state sostenute da una progettazione, da
un'attività preparatoria ed infine da una realizzazione precise ed attente. All'originalità della proposta si affianca l'inventiva con cui sono
state pensate soluzioni semplici ed efficaci ai problemi sperimentali
che si presentavano.
Il lavoro è stato svolto in collaborazione con l’ISTITUTO GAS IONIZZATI,
progetto RFX del C.N.R. di Padova
Premio Cesare Bonacini 2003
RELAZIONE DEL DOCENTE COORDINATORE
I PARTECIPANTI
Il lavoro è stato portato aventi da un piccolo gruppetto di alunni, ben motivato, della classe 5° Tecnologico del Liceo Scientifico di Montebelluna
(TV). Le esperienze sono state effettuate nel Laboratorio della nostra
scuola dove abbiamo trascorso molti pomeriggi e si sono svolte con le
modalità di un RICERCA vera e propria. Partendo da un’idea fondamentale
sono stati sviluppati vari aspetti teorici e sperimentali, fino ad ottenere un
quadro abbastanza coerente dei fenomeni analizzati.
L’IDEA
L’idea della proposta da me fatta agli alunni di quinta A Tecnologico per la
realizzazione delle esperienze qui presentate, è nata da una serie di discussioni che ho avuto con alcuni ricercatori dell’Istituto Gas Ionizzati di
Padova, riguardo ai moti di deriva elettrica in un plasma da fusione nucleare. In caso di presenza contemporanea di un campo elettrico e di un
campo magnetico le particelle caricher acquistano,
in condizioni stazionarie
r
r E∧B
che da luogo ad un movimento
una velocità di deriva elettrica: v =
B2
globale del plasma, nel senso che questo moto è indipendente dal segno
della carica elettrica, come pure dalla massa, di ciascuna particella.
Una situazione analoga doveva allora presentarsi anche in presenza di
campi elettrici e magnetici in un liquido. Da qui la proposta, subito accolta
con entusiasmo da parte di un gruppetto di alunni.
Vari tentativi di mettere a punto le esperienze, durante il corso dell’anno,
si sono rivelati infruttuosi, con conseguente delusione e momentanei scoraggiamenti. Ogni volta però, dopo un’attenta analisi, nasceva da parte di
qualche alunno una nuova idea da “provare sperimentalmente”, che rimetteva in moto l’entusiasmo di tutto il gruppo.
Una svolta significativa si è avuta quando l’Istituto Gas Ionizzati ci ha prestato una serie di calamite in grado di generare intensi campi magnetici,
utilizzando i quali, finalmente, “l’acqua si è mossa”.
Un’altra importante “sorgente” di motivazione e spunto per la messa a
punto di nuove esperienze è stata la decisione di inquadrare il lavoro
nell’ambito della proposta del “Premio Bonacini 2003”.
Il docente Coordinatore
Emanuele Spada.
2
3
Premio Cesare Bonacini 2003
INTRODUZIONE
IL PRINCIPIO DI AZIONE E REAZIONE
Il fatto di tirare o premere qualcosa e sentirsi contemporaneamente tirati o premuti fa
parte delle nostre esperienze quotidiane. Non è però necessario che i corpi “si tocchino”.
Anzi, da un punto di vista microscopico, anche l’interazione di “contatto” tra i corpi è
un’interazione di tipo elettrico e quindi un’interazione a distanza che si esercita nella direzione congiungente i due corpi. Molto simile a questa è anche l’interazione gravitazionale. Siamo disposti quindi, in modo naturale ad ammettere la validità del “Principio di
Azione e Reazione” sia per le interazione elettriche che per quelle gravitazionali.
Maggiori perplessità nascono invece quando consideriamo un altro tipo di interazione,
molto più strana e lontana dal nostro modo di percepire le interazioni: l’interazione magnetica. Non tanto l’interazione magnetica tra due calamite, molto simile a quella elettrica, bensì ci lascia perplessi l’applicabilità del Principio di Azione e Reazione all’interazione
che si manifesta tra una carica libera, in movimento e la calamita stessa. In questo caso,
quando una particella carica, libera di muoversi, passa “sopra” una calamita, essa risente
di una forza perpendicolare alla direzione del suo moto. Il Principio di Azione e Reazione
prevede che la calamita a sua volta risenta di una forza uguale e contraria e dunque
sempre perpendicolare al moto della particella stessa. La calamita agisce sulla carica in
moto tramite il campo magnetico da essa prodotto.
Può questa particella, libera di muoversi, effettuare un’analoga forza sulla calamita? In
quale modo agisce? In quale modo viene esercita una forza sulla calamita, perpendicolare
al moto della particella?
Abbiamo voluto affrontare questo problema da un punto di vista sperimentale.
Innanzitutto ci siamo procurati un sistema nel quale le cariche potessero muoversi abbastanza liberamente. Non abbiamo pertanto preso in considerazione il movimento di cariche all’interno di conduttori solidi (ad esempio all’interno di un filo di rame), in quanto le
cariche sono abbastanza libere di muoversi soltanto lungo il conduttore. Viceversa, quando la forza di Lorentz agisce sulle cariche, il movimento traversale che dovrebbe aver
luogo, viene fortemente limitato dai legami presenti nella struttura reticolare del solido.
Abbiamo preferito allora, utilizzare un liquido, nel quale fosse presente un sufficiente
numero di particelle cariche.
L’esperienza è stata organizzata in 3 parti.
Nella prima parte abbiamo analizzato quantitativamente il movimento di cariche elettriche all’interno di un liquido. Nella seconda abbiamo caratterizzato in modo piuttosto qualitativo quale potesse essere l’effetto delle calamite, sull’ambiente circostante.
Nell’ultima parte, infine, ci siamo occupati dell’interazione tra le calamite e le cariche in
movimento; studiando prima l’effetto delle calamite sulle cariche elettriche in movimento
e poi quello opposto, ossia quello esercitato dalle cariche in movimento sulle calamite.
MOVIMENTO DELLE CARICHE ELETTRICHE IN UN LIQUIDO
CARATTERIZZAZIONE QUALITATIVA
DEL CAMPO MAGNETICO DELLE CALAMITE
INTERAZIONE TRA CALAMITE E CARICHE IN MOVIMENTO
Calamite ferme, Cariche in moto accelerato
Cariche in moto uniforme, Calamite accelerate
4
Premio Cesare Bonacini 2003
STUDIO DEL MOVIMENTO DI CARICHE ELETTRICHE IN UN LIQUIDO
Primi tentativi
Nella prima serie di esperimenti, che verranno descritti in questa sezione, il nostro intento è stato quello di analizzare il moto delle cariche elettriche in un liquido.
Il liquido che abbiamo utilizzato è stata l’acqua. La conduzione elettrica dell’acqua distillata è risultata essere troppo piccola per i nostri scopi. Abbiamo quindi pensato di sciogliere nell’acqua un sale, in modo da arricchirla di ioni, sia positivi che negativi.
I primi esperimenti li abbiamo fatti sciogliendo in acqua del sale da cucina (NaCl), ma
abbiamo subito incontrato due difficoltà. La prima è stata quella che durante
l’esperimento veniva prodotto un nauseabondo odore di “candeggina”. Infatti il cloro gassoso prodotto all’anodo, reagiva con la soluzione di NaCl per dare origine ad una soluzione di ipoclorito di sodio NaClO (la candeggina appunto). In secondo luogo, le misure di
intensità di corrente e di differenza di potenziale, variavano durante le prove ed inoltre si
osservava che l’anodo anneriva gradualmente, sporcando di conseguenza la nostra soluzione. Alla fine di ogni esperienza inoltre, dopo aver spento il generatore di tensione, si
poteva verificare l’esistenza di una differenza di potenziale residua ai capi degli elettrodi
(fenomeno della polarizzazione) dovuto alle reazioni chimiche che avvengono sugli elettrodi stessi.
Per evitare la formazione di candeggina, abbiamo successivamente utilizzato come elettrolita il solfato di sodio (Na2SO4). In questo caso, nessuno dei due ioni (Na+ e SO4--)
partecipa alle reazioni agli elettrodi, dove vengono semplicemente liberati O2 e H2 in forma gassosa. Si è così ottenuto un sostanziale miglioramento delle condizioni di lavoro
(nessun odore di candeggina), rimaneva tuttavia il problema dell’annerimento dell’anodo
con conseguente intorbidamento della soluzione. Neppure la sostituzione delle lamine di
rame con due lamine d’argento ha migliorato sostanzialmente questa situazione.
La “Giusta Soluzione”
Abbiamo infine utilizzato una soluzione di solfato di rame (CuSO4) e gli elettrodi stessi di
rame. In questo caso si ottiene, almeno da un punto di vista teorico1, il duplice vantaggio
di non modificare la soluzione durante l’esperimento e di evitare il fenomeno della polarizzazione. Il processo chimico che avviene, può essere semplicemente descritto in modo
complessivo come un trasferimento di rame dall’Anodo al Catodo.
In quello che segue riporteremo soltanto i dati
ottenuti con soluzioni di CuSO4.
Nella prima esperienza abbiamo voluto verificare
la validità o meno della prima legge di Ohm nella
soluzione di CuSO4. Nella foto qui riportata è
messo in evidenza il semplice apparato sperimentale utilizzato, costituito essenzialmente da
una vaschetta di vetro, contenente la soluzione e
dalle lamine di rame utilizzate come elettrodi.
Foto (1) della bacinella e degli elettrodi utilizzati nelle esperienze 1, 2, 3, 4.
1
Antonio Rostagni, FISICA GENERALE vol. 2, pag 932, UTET (1978).
5
Premio Cesare Bonacini 2003
ESPERIENZA N°1: LEGGE DI OHM
OBIETTIVO:
MATERIALI:
MISURA DELL’INTENSITÀ DI CORRENTE IN FUNZIONE DELLA DIFFERENZA DI POTENZIALE
VOLTMETRO, AMPEROMETRO, 2 ELETTRODI DI RAME (20 X 100 MM), CAVETTI DI COLLEGAMENTO, GENERATORE DI TENSIONE, BACINELLA DI VETRO, SOLUZIONI DI CuSO4 (CONC.:
1M.), METRO.
L’esperienza consiste nel misurare l’intensità della corrente che passa attraverso la soluzione in cui sono immersi i
due elettrodi (posti a una distanza di 130 mm) al variare della differenza di potenziale imposta dal generatore di tensione. La differenza di potenziale è stata misurata ai capi degli elettrodi. I dati sono di seguito riportati.
d.d.p. (V)
7,5
9,0
11,5
14,0
16,0
18,0
20,0
21,5
24,0
26,0
I (A)
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
Intensità di Corrente Elettrica in funzione della
Differenza di Potenziale
I = 0,0964 ddp - 0,1153
3
2,5
2
I (A)
n
1
2
3
4
5
6
7
8
9
10
1,5
1
0,5
0
0
5
10
15
20
25
30
d.p.p. (V)
dati
incertezze
Figura 1
L’incertezza sulle misure di d.d.p. sono di ±0,5 V fino al 4° dato, e di ±1 V dal 5° in poi in quanto sono state usate
due diverse scale del voltmetro: 0 – 15 e 0 – 50. L’incertezza per l’intensità di corrente è di ± 0,2 A.
Alcune osservazioni qualitative.
a) Le misure di differenza di potenziale e l’intensità di corrente elettrica effettuate sono
riproducibili, ossia ripetendo le stesse misure in momenti successivi, non abbiamo mai
evidenziato variazioni significative rispetto ai valori qui riportati.
b) La soluzione non presentava modifiche apprezzabili nell’intensità del suo colore azzurro.
c) L’Anodo non presentava sostanziali variazioni nella sua struttura. (Eccettuata una lieve colorazione nera).
d) Il Catodo presentava un deposito di rame abbastanza regolare su tutta la superficie
affacciata verso l’Anodo.
I dati misurati (Fig. 1) rivelano un andamento lineare della corrente elettrica in funzione
della differenza di potenziale. La retta però non passa per l’origine, evidenziando probabilmente il fenomeno della polarizzazione, forse dovuta ad un effetto di ossidazione
dell’Anodo. L’andamento lineare ci rafforza comunque nell’idea che la legge di Ohm è valida, con buona approssimazione, anche nei liquidi.
CONCLUSIONE: La corrente elettrica nella soluzione utilizzata, segue con buona approssimazione la legge di Ohm: (I/V = costante).
Una volta stabilita la validità della legge di Ohm, abbiamo indagato su quali siano i parametri che possono influenzare la Resistenza elettrica della soluzione. I parametri presi
in considerazione sono: la molarità (Esp. 2), la distanza fra gli elettrodi (Esp. 3), la superficie degli elettrodi (Esp. 4).
6
Premio Cesare Bonacini 2003
ESPERIENZA N°2:
OBIETTIVO:
MATERIALI:
LA MOLARITA’
MISURA DEL RAPPORTO TRA INTENSITÀ DI CORRENTE E DIFFERENZA DI POTENZIALE IN
FUNZIONE DELLA MOLARITÀ DELLA SOLUZIONE
VOLTMETRO, AMPEROMETRO, 2 ELETTRODI DI RAME (20 X 100 MM), CAVETTI DI COLLEGAMENTO, GENERATORE DI TENSIONE, BACINELLA DI VETRO, SOLUZIONI DI CuSO4 (CONC.:
0,01M. 0,05M. 0,1M. 0,25M. 0,5M. 1M.), METRO.
Questa esperienza è stata effettuata allo scopo di studiare in che modo la concentrazione del sale nella soluzione influisca sulla conduzione di corrente elettrica nella soluzione. Abbiamo effettuato l’esperimento, fissando una differenza di potenziale ai capi degli elettrodi pari a 7V e variando di volta in volta la molarità della soluzione. La distanza
tra gli elettrodi utilizzata è di 130 mm.
M (mol/L)
0,01
0,05
0,1
0,25
0,5
1
I (mA) / d.d.p. (V)
2,9
7,1
17,1
28,6
42,9
114,3
Rapporto tra Intensità di Corrente Elettrica e differenza di
potenziale in funzione della Molarità della soluzione
ddp costante = 7V
I / ddp = 109,39 M
I (mA) / ddp (V)
n
1
2
3
4
5
6
150,0
100,0
50,0
0,0
0
0,2
0,4
0,6
0,8
1
1,2
M (mol/l)
L’incertezza sulla misura di I è ±5 mA, su d.d.p. è
±0,5 V e per M ±0,001 mol/L. Le incertezze nel
grafico non si vedono perché sono troppo piccole.
Dati
incertezze
Figura 2
CONCLUSIONE: Il grafico di Fig.2 mette in evidenza una proporzionalità diretta tra la molarità (ossia la quantità di ioni presenti nella soluzione) ed il rapporto I/V.
ESPERIENZA N°3:
L’esperienza consiste nell’individuare la relazione tra intensità
di corrente e distanza fra gli elettrodi, per una fissata differenza di potenziale. L’esperienza è stata effettuata avendo
l’accortezza di mantenere gli elettrodi sempre paralleli tra loro. Le misure effettuate sono qui di seguito riportate:
n
d (mm)
1
2
3
4
5
6
7
8
9
10
11
12
20
30
40
50
60
70
80
90
100
110
120
130
I (A) / ddp
(V)
0,77
0,55
0,42
0,33
0,27
0,23
0,20
0,17
0,15
0,13
0,13
0,12
Rapporto tra Intensità di Corrente Elettrica e differenza
di potenziale in funzione della Distanza fra gli elettrodi
ddp costante = 6V.
1,50
I (A) / ddp (V)
MATERIALI:
MISURA DEL RAPPORTO TRA INTENSITÀ DI CORRENTE E DIFFERENZA DI POTENZIALE IN
FUNZIONE DELLA DISTANZA FRA GLI ELETTRODI
VOLTMETRO, AMPEROMETRO, 2 ELETTRODI DI RAME (20 X 100 MM), CAVETTI DI COLLEGAMENTO, GENERATORE DI TENSIONE, BACINELLA DI VETRO, SOLUZIONE DI CuSO4 (CONC.:
1M), METRO.
1,00
0,50
0,00
-0,50
0
20
40
60
80
100
dati
140
incertezze
Figura 3.1
Linearizzazione
I / ddp = 15,87 / d
1,2000
1,0000
0,8000
0,6000
0,4000
0,2000
0,0000
-0,2000 0
0,01
0,02
0,03
0,04
1/d (mm)
L’incertezza sulle misure della distanza sono di ±1 mm, mentre quelle relative alla misura dell’intensità di corrente hanno
120
d (mm)
I (A) / ddp (V)
OBIETTIVO:
LA DISTANZA TRA GLI ELETTRODI
Dati
Incertezze
Figura 3.2
0,05
0,06
0,07
7
Premio Cesare Bonacini 2003
un valore di ±0,2 A. La differenza di potenziale è stata mantenuta costante a 6 V e l’incertezza sulla misura è ±0.5 V.
In Fig 3.1 vengono riportati i dati misurati. L’andamento iperbolico dei dati viene confermato nel grafico
“linearizzato” riportato in Fig 3.2, dove nell’asse delle ascisse abbiamo riportato il reciproco della distanza tra gli
elettrodi.
CONCLUSIONE: I grafici di Fig.3.1 e 3.2 mettono in evidenza una proporzionalità inversa
tra la distanza degli elettrodi ed il rapporto I/V.
ESPERIENZA N°4
OBIETTIVO:
MATERIALI:
LA SUPERFICIE DEGLI ELETTRODI
MISURA DEL RAPPORTO TRA INTENSITÀ DI CORRENTE E DIFFERENZA DI POTENZIALE IN
FUNZIONE DELLA SUPERFICIE DEGLI ELETTRODI
VOLTMETRO, AMPEROMETRO, 2 ELETTRODI DI RAME (20 X 100 mm), CAVETTI DI COLLEGAMENTO, GENERATORE DI TENSIONE, BACINELLA DI VETRO, SOLUZIONE DI CuSO4 (CONC.:
1M), NASTRO ISOLANTE (h 19 mm), METRO.
L’esperienza consiste nella misura dell’intensità di corrente elettrica, al variare della superficie degli elettrodi. Per variare la superficie degli elettrodi abbiamo gradualmente isolato le due superfici con del nastro isolante. Nella Foto 1 si
vedono i due elettrodi ricoperti per metà dal nastro isolante. Durante l’esperienza abbiamo mantenuto costante il
valore della differenza di potenziale (8V) e la distanza tra gli elettrodi (130 mm).
S(mm²)
0
100
480
860
1240
1620
2000
I (A)/ddp (V)
0,067
0,055
0,042
0,030
0,017
0,002
1,000
h (mm)
20
20
20
20
20
20
20
L (mm)
0
5
24
43
62
81
100
Rapporto tra Intensità di Corrente Elettrica e differenza
di potenziale in funzione della Superficie degli Elettrodi
con ddp costante = 8V
I / ddp = 3E-05 S
0,090
0,070
0,050
I (A) / ddp (V)
n
1
2
3
4
5
6
7
0,030
0,010
-0,010 0
Le incertezze sulle misure di intensità di corrente e di differenza di
potenziale, sono analoghe a quelle delle esperienze precedenti. Per
quanto riguarda l’incertezza delle misure delle superfici rettangolari
degli elettrodi, si è tenuto conto dell’incertezza di misura su entrambe le dimensioni
500
1000
1500
2000
2500
-0,030
-0,050
S (mm²)
incertezze
dati
Lineare (dati)
Figura 4
CONCLUSIONE: Il grafico di Fig.4 mette in evidenza
una proporzionalità diretta tra la superficie degli
elettrodi ed il rapporto I/V.
NOTA: Dopo aver eseguito queste esperienze ed esserci convinti della validità della legge
di Ohm abbiamo voluto misurare direttamente con un resistometro la resistenza elettrica
della soluzione, al variare di: molarità, distanza e superficie degli elettrodi. I dati misurati, non riportati in questa relazione, risultano perfettamente in accordo con quelli dedotti
dal rapporto V/I.
RIASSUNTO DELLE RELAZIONI TROVATE
Dalle esperienze fino ad ore effettuate, abbiamo dedotto
•
La validità della legge di Ohm:
I = α ⋅ ddp.
•
Proporzionalità diretta tra Intensità
di corrente e differenza di potenziale
⇒
I
1
= kost = .
V
R
La dipendenza del rapporto I/ddp dalle variabili M, S, d (Molarità, Superficie, distanza fra gli elettrodi).
I
= β ⋅ M.
ddp
Proporzionalità diretta tra Intensità di corrente e Molarità
⇒
I
M ⋅S 1
=K⋅
= .
ddp
d
R
8
Premio Cesare Bonacini 2003
I
γ
= .
ddp d
I
= δ ⋅ S.
ddp
Proporzionalità inversa tra Intensità di corrente e distanza
fra gli elettrodi
Proporzionalità diretta tra Intensità di corrente e Superficie
E quindi:
R=
K* d
⋅ .
M S
da cui, ponendo
ρ=
K*
.
M
dove ρ è il coefficiente di resistività della soluzione.
Questo dipende in modo inversamente proporzionale dalla concentrazione molare di soluto nella soluzione.
Nella figura accanto viene riportato il valore I/V in
funzione di (MS/d).
d
.
S
Rapporto tra Intensità di Corrente Elettrica e differenza di
potenziale in funzione del rapporto tra Superficie e Distanza
fra gli elettrodi e della Concentrazione molare
ddp costante = 6V.
1,2000
I / ddp = 0,0079 M*S / d
1,0000
I (A) / ddp (V)
1
M ⋅S
M ⋅ S −1
=K⋅
= 0,0079 ⋅
Ω .
R
d
d
1
1
Ω ⋅ mol
K* = =
= 130
.
K 0,0079
m⋅L
130
ρ=
Ω ⋅ m.
M
STIMA
R= ρ⋅
si ottiene
0,8000
0,6000
0,4000
0,2000
0,0000
-0,2000
0
20
40
60
80
100
M (mol/L) * S (mm²) / d (mm)
dati
incertezze
Figura 5
DELLA VELOCITÀ MEDIA DEGLI IONI NELLA SOLUZIONE
Nella dissociazione di una mole di CuSO4 si ottengono due moli di ioni: Cu++ e SO4-- ciascuno di carica pari, in modulo, a 2e (e=carica del protone).
Si ha che l’intensità di corrente elettrica è:
I =
∆Q
= q ⋅ n ⋅ s ⋅ v = 4 e ⋅ n0 ⋅ s ⋅ v
∆t
dove: e = 1.6*10-19 C
s = superficie degli elettrodi = 2000 mm2
n0 =
n° molecole di CuSO4
= n° Avogadro ⋅ M
Volume soluzione
M=
n° moli soluto
Volume soluzione
Utilizzando:
v=
M = uno molare = 1 M =1 mol/L = 1000 mol/m3
n° Avogadro = 6.023*1023 1/mol
n = 6.023*1023 mol-1 1000 mol/m3 = 6.023*1026 m-3
intensità di corrente I = 1 A
si ottiene infine:
I
=
q⋅n⋅s
1A
4 ⋅ 1,6 ⋅ 10 −19 C ⋅ 6,023 ⋅ 10 26
1
⋅ 2 ⋅ 10 −3 m 2
3
m
≅ 1 ⋅ 10 −6
m
.
s
120
9
Premio Cesare Bonacini 2003
STUDIO DEL CAMPO MAGNETICO GENERATO DALLE CALAMITE
La seconda parte
del nostro studio
consiste
nell’esaminare
qualitativamente
CALAMITA
l’azione del campo
magnetico
delle
calamite
sull’ambiente circostante.
Per ottenere riFoto 2
sultati evidenti e
buone misurazioni
sperimentali abbiamo
ritenuto
opportuno servirci
di calamite dalle
ridotte dimensioni
ma comunque efFoto 4. Confronto tra una
calamita e una moneta
ficaci.
L’Istituto
Foto 3. Carico sostenuto da una sola
da un Euro
calamita
Gas Ionizzati del
C.N.R di Padova,
ci ha prestato un kit di 80 calamite (modello: N35 composte da Neodimio, Ferro, Boro
prodotte dalla ditta “Alga Magneti”) in grado di generare campo magnetico molto intenso
nonostante le ridotte dimensioni (ciascuna calamita sviluppa un campo magnetico ≅ 1 T
sulla superficie). Nella figura si può notare il fatto che una singola calamita è in grado di
sorreggere circa 1,7 chilogrammi di peso. Conoscendo il peso massimo sorretto da una
singola calamita, possiamo fare una stima del campo magnetico sulla sua superficie.
STIMA DEL CAMPO MAGNETICO DELLE CALAMITE
In generale il legame tra forza F ed energia potenziale U è dato dalla relazione:
Ad esempio nel caso gravitazionale “uniforme” si ha:
U = mgx e F =
F=
dU
.
dx
dU
= mg
dx
Possiamo adottare un procedimento simile per stimare la forza esercitata alla superficie
di una delle nostre calamite in funzione del campo magnetico superficiale.
Stimiamo il campo magnetico superficiale della calamita. L’energia magnetica, nell’ipotesi
di un campo magnetico uniforme sulla superficie della calamita, si può esprimere come:
U = uB Sx.
dove:
ma
U energia magnetica in una certa regione di spazio (nel nostro caso un cilindro
con una delle due basi coincidenti con una delle basi della calamita);
S superficie di base delle calamita;
x altezza del cilindro;
uB densità di energia magnetica.
F = U ' (x ) = uB ⋅ S .
della calamita e
B2
S
2µ0
B2
uB =
2 µ0
; B è il campo magnetico sulla superficie
µ 0 è la permeabilità magnetica del vuoto.
Otteniamo allora:
F=
dove
10
Premio Cesare Bonacini 2003
e da questo possiamo ricavare B:
B=
2 Fµ0
=
S
2 F ⋅ 4π 10−7
S
I valori di S ed F sono ottenuti sperimentalmente.
S = π ⋅ (0,45 cm ) ⋅ 0,636 cm 2 = 0,636 ⋅ 10 −4 m 2 .
N
F = m ⋅ g = 1,7 Kg ⋅ 9,81
= 16,6 N . da cui
Kg
2
B=
mT
A = 8,09 ⋅ 10−1T ≅ 1T
2
2 ⋅ 16,6 N ⋅ 4 ⋅ π ⋅ 10 − 7
π ⋅ 2,025 ⋅ 10− 5 m
che ci fornisce una stima del campo magnetico sulla superficie della calamita di 1 T.
Le caratteristiche tecniche dei magneti, trovate nel sito Internet della ditta produttrice,
sono qui sotto riportati.
Modello
Campo Magnetico sulla superficie
(G) / (Tesla)
T Max (°C)
N35
11600-12400 /1,16-1,24
80
Si vede come i dati forniti dal sito siano dello stesso ordine di grandezza del valore da noi
stimato utilizzando il massimo carico sorretto dal magnete.
CAMPO MAGNETICO E DISTANZA
Fissato il valore del campo magnetico sulla superficie della calamita. È interessante capire
in che modo esso diminuisca allontanandoci da essa. Per far questo abbiamo assimilato il
comportamento della calamita ad un anello percorso da corrente:
B=
µ0 I ⋅ S
(I = in⋅
2π h 3
tensità di corrente che attraversa il solenoide, S = superficie della sezione del solenoide,
h = distanza lungo l’asse dal centro dell’anello), e da questo abbiamo ricavato i dati necessari per costruire un grafico (fig. 6.1) del campo magnetico (B) in funzione della distanza dalla superficie, lungo l’asse (h) sfruttando la seguente relazione ricavata dalla
legge appena sopra descritta.
3
h 
B = B0 ⋅  0  (B = campo magne h
1,4
1,2
B (Tesla)
tico ad una distanza h dal centro
della calamita, B0 = campo magnetico sulla superficie della calamita, h0 = distanza della superficie
dal centro della calamita). Dal grafico si vede che a distanze molto
piccole il campo magnetico ha
un’intensità molto elevata, ma appena ci spostiamo di qualche millimetro questo valore decresce
molto rapidamente divenendo trascurabile a circa due centimetri
dalla superficie della calamita.
Valore del Campo magnetico in funzione della distanza
dalla calamita lungo l'asse
1
0,8
0,6
0,4
0,2
0
0
0,25 0,5 0,75
1
1,25 1,5 1,75
Distanza (cm)
Figura 6.1
2
2,25 2,5 2,75
3
3,25
11
Premio Cesare Bonacini 2003
B (Tesla
Il grafico di figura 6.2 da un’idea di quale sia l’andamento del campo magnetico generato
da due magneti affacciati l’uno all’altro (N/S N/S) come nella foto 7. Per ricavare i dati
abbiamo utilizzato un procedimento
Valore del Campo magnetico tra due calamite
di calcolo analogo a quello utilizzato
affacciate (NSNS) in funzione della distanza lungo
per il grafico precedente. In questo
l'asse
1,4
caso sono stati sommati i campi ma1,2
gnetici. Il grafico che ne risulta è
1
quello di figura 6.2, e anche in que0,8
0,6
sto caso si può notare come il campo
0,4
magnetico sia molto intenso se ci po0,2
niamo molto vicino ai magneti, ma
0
0 0,25 0,5 0,75 1 1,25 1,5 1,75 2 2,25 2,5 2,75 3 3,25
diminuisca molto rapidamente se ci
Distanza (cm)
allontaniamo di qualche centimetro.
Figura 6.2
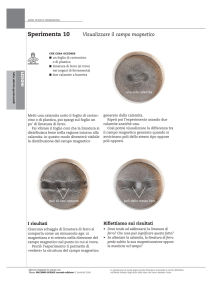
LE LINEE DI CAMPO
Infine, per visualizzare il campo magnetico, delle nostre
calamite,
abbiamo ottenuto
delle immagini che potessero
dare un’idea dell’andamento
delle linee del campo magnetico. Ottenere delle buone immagini di questo fenomeno
non è stato molto semplice,
infatti, il problema principale
consisteva nell’individuazione
Foto 5
Foto 6
d'un “elemento” viscoso adatto
dove porre la limatura di ferro, altrimenti attratta in modo eccessivamente intenso dalle
nostre calamite. In vari tentativi abbiamo utilizzato l’olio comune, il gel per capelli, l’olio
per motori Diesel. Quest’ultima soluzione è risultata la migliore, sia in termini di praticità
che di efficacia. Per rendere visibili le linee di campo magnetico, ci siamo serviti di un
contenitore trasparente dove avevamo mescolato la limatura di ferro con quest’olio
molto denso. Sotto il contenitore, ad una distanza di circa mezzo centimetro, abbiamo
posto i magneti, opportunamente fissati con dello scotch ad una lastra di plexiglas, e abbiamo posto tutto sopra il piano di uno scanner. È stato utilizzato uno scanner perché riprendendo la situazione da sotto permetteva di visualizzare anche i magneti. Le immagini
ottenute sono quelle nelle foto 5, 6, 7.
La foto 5 illustra come una calamita (la faccia S parallela al fondo del contenitore trasparente) orienti la limatura di ferro con il caratteristico andamento radiale, questo perché le linee di campo magnetico escono da questa superficie per poi curvarsi e richiudersi
nell’altra faccia sottostante. Nella foto 6 invece, la calamita ha l’asse parallelo al fondo
del contenitore: possiamo osservare come realmente le linee di campo escano da una
faccia ed entrino nell'altra. Avremmo ottenuto
un'immagine ancora più significativa immergendo la calamita in un contenitore pieno d'olio e
limatura di ferro, e facendo una foto che mostrasse i due effetti sommati in una configurazione tridimensionale. Infine, nell’ultima foto
abbiamo affacciato due calamite N/S N/S in
modo da verificare che nello spazio compreso
fra esse il campo magnetico possa effettivamente essere uniforme.
Foto 7
N
S N
S
12
Premio Cesare Bonacini 2003
INTERAZIONE TRA CORRENTI ELETTRICHE E CAMPO MAGNETICO
L’ACQUA SI MUOVE IN PRESENZA DI UNA CALAMITA
L’ultima parte del nostro studio consiste nell’indagare come possano interagire in un fluido le particelle cariche in movimento (corrente elettrica), con il campo magnetico generato dalle calamite. Ponendo una calamita appena sopra la superficie della soluzione, e
facendo attraversare la soluzione da una corrente elettrica, si nota un movimento circolare dell’acqua come rappresentato nello Schema 1. Se si rovescia la calamita anche il
movimento dell’acqua avviene in direzione opposta a quella in cui si muoveva precedentemente. Questo movimento dell’acqua viene inoltre maggiormente evidenziato se si pone sotto la bacinella un’altra calamita, orientata nello stesso modo della prima.
L’interpretazione di questo fenomeno può essere
ricondotta all’effetto della forza di Lorentz
r
r r
F = q ⋅ v ∧ B sugli ioni in movimento. Gli ioni pre-
senti in soluzione sono sempre di due tipi: positivi
e negativi. Essi si muovono a causa del campo
elettrico generato dai due elettrodi, in direzioni
opposte e dunque hanno velocità opposte. Questo
fa si che la forza di Lorentz agente sui due tipi di
ioni abbia in entrambi i casi lo stesso verso. In
CALAMITA
questo movimento gli ioni trascinano le molecole
ELETTRODI
di acqua polarizzate, dando luogo ad un moviSchema 1
mento globale di tutto il fluido. Il fatto che il movimento del liquido, tra le calamite risulti perfettamente perpendicolare alla direzione della corrente elettrica è giustificato dal fatto che la
velocità degli ioni è molto piccola (v ≈ 10-3mm/s) e dunque il movimento prodotto dalla
forza di Lorentz è praticamente parallelo alla forza stessa.
Partendo da questa semplice osservazione è nata l’idea di costruire una pompa magnetica (o meglio una pompa magneto-idrodinamica) sfruttando l’interazione tra il campo magnetico prodotto dalle calamite e la corrente che attraversa la soluzione.
ESPERIENZA:
OBIETTIVO:
LA POMPA MAGNETICA
STUDIO DELL’INTERAZIONE TRA COMPO MAGNETICO E CORRENTE ELETTRICA, MANTENENDO LE
CALAMITE FERME E LASCIANDO LIBERA DI MUOVERSI LA SOLUZIONE ALL’INTERNO DELLA
PIROFILA.
MATERIALI:
AMPEROMETRO, VOLTMETRO, 2 ELETTRODI DI RAME
OPPORTUNAMENTE SAGOMATI PER LA CONFORMAZIONE CIRCOLARE DEL
RECIPIENTE, STATIVO, MORSETTI, 2 PIASTRE DI METALLO, 2 PIROFILE
DI VETRO DI FORMA CIRCOLARE, CAVETTI DI COLLEGAMENTO,
GENERATORE DI TENSIONE, SOLUZIONE DI Cu SO4 (CONC. 1M), 12
MAGNETI MODELLO N35, CRONOMETRO.
Per prima cosa
abbiamo
costruito un circuito d’acqua.
Per far questo
abbiamo posto
Foto 8
la pirofila più
piccola (diametro 15cm) all’interno della pirofila più grande
(diametro 22cm), aggiungendo all’interno della pirofila più
piccola un peso per far si che la soluzione una volta versata
nel contenitore rimanesse solo nello spazio vuoto tra i due
recipienti e non si infiltrasse anche sotto il fondo del contenitore più piccolo.
Foto 9
13
Premio Cesare Bonacini 2003
Fatto questo abbiamo fissato 12 magneti su due piastre metalliche. I magneti sono stati disposti su di una piastra tutti
con il polo NORD rivolto verso la piastra stessa, nell’altro supporto in
modo esattamente opposto (polo SUD rivolto verso la piastra metallica.
Vedi foto 8). Le due serie di calamite sono state poi disposte una affacciata all’altra in modo da ottenere un campo magnetico uniforme, cioè
con delle linee di campo rette (vedi foto n°7) .La prima piastra è stata
quindi posta al di sotto della pirofila grande in modo tale che i magneti
toccassero il fondo di vetro, la seconda è stata sospesa appena sopra la
superficie della soluzione utilizzando uno stativo (figura 9).
Abbiamo poi messo gli elettrodi in corrispondenza delle piastre con i
magneti, in modo da generare una corrente elettrica nella zona in cui la
soluzione è immersa nel campo magnetico delle calamite.
Gli elettrodi sono stati collegati al generatore di tensione e con un colleFoto 10
gamento in serie abbiamo collegato anche l’amperometro per misurare
l’intensità di corrente.
Inoltre, ai capi degli elettrodi, è stato collegato un voltmetro per controllare che il voltaggio non raggiungesse valori troppo alti che potevano
danneggiare il generatore di tensione.
Messa a punto tutta la strumentazione abbiamo versato la soluzione di
solfato di rame nella pirofila fino a raggiungere un livello di circa 1 cm di
altezza.
L’esperienza è consistita nella misura, per ogni valore fissato di corrente,
del tempo impiegato (periodo) da una pallina di polistirolo che galleggiava sulla superficie della soluzione per compiere quattro giri completi attorno al nostro circuito. Sono stati fatti fare 4 giri in modo da ridurre
Foto 11
l’errore di misura sul tempo.
DATI MISURATI
Volume soluzione
Sup. Elettrodi
n° magneti
R MAX
r min
distanza fra magneti
distanza fra magneti posti sotto e soluzione
livello soluzione
n
1
2
3
4
5
5
7
8
9
10
11
12
13
0,25
850
6+6
220
150
60
5
10
I (A)
2,0
2,2
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
4,6
T (s) x 4
66,38
60,01
53,93
49,45
42,62
41,5
39,69
36,57
32,71
32,2
33,94
31,6
30,1
T (s)
16,7
15,0
13,5
12,4
10,7
10,4
9,9
9,1
8,2
8,1
8,5
7,9
7,5
L
mm²
mm
mm
mm
mm
mm
14
Premio Cesare Bonacini 2003
ANALISI DEI DATI MISURATI
Periodo in funzione dell'Intensità di Corrente
Si deduce dai risultati ottenuti che la forza
(di Lorentz) agente sul fluido e la velocità
media acquisita dallo stesso sono fra loro
proporzionali. Questo significa che siamo
in presenza di forze viscose che si oppongono al moto del fluido. L’equazione della
dinamica può essere scritta nella forma:
r
r
m ⋅ a. = FLorentz − kv
dove
F Lorentz
80
T (s)
60
40
20
0
0
1
2
3
4
5
6
I (A)
Incertezze
Dati
Figura 7
Velocità in funzione dell'Intensità di Corrente
velocità = 34,601 I
200
v (mm/s)
I grafici riportati in Figg. 7 ed 8 mettono
in evidenza una diretta proporzionalità
tra la corrente elettrica e la velocità media con cui si muovono le palline di polistirolo, poste sulla superficie dell’acqua.
E’ corretto parlare di velocità media del
fluido, in quanto l’osservazione della pallina durante l’esperienza mostra come
essa rallenti molto la sua velocità quando
si trova vicino ai bordi del circuito e al
contrario vada alla velocità massima
quando si trova al centro. Inoltre, quando si toglie la corrente dal circuito (così
facendo si toglie la forza motrice della nostra pompa) la pallina di polistirolo diminuisce gradualmente la sua velocità fino a
fermarsi.
150
100
50
0
0
1
2
3
4
5
6
I (A)
Incertezze
Dati
Figura 8
rappresenta la forza di Lorentz e la costante k dipende dalla viscosità del fluido e da
parametri geometrici (non valutati in questa esperienza). La condizione stazionaria
( a = 0 ) si ottiene quanto la velocità media del fluido raggiunge il valore
r
FLorentz k
proporzionale alla corrente elettrica.
Conclusione: L’esperienza svolta evidenzia come le calamite possano esercitare una forza sulla corrente elettrica che attraversa la soluzione e come questa forza metta in moto
tutto il fluido. Inoltre si verifica una diretta proporzionalità tra la corrente e la velocità
media del fluido.
Il movimento dell’acqua nella Pompa Magnetica è conseguenza della forza esercitata dalla
calamita (mediante il campo magnetico) sulle cariche elettriche in movimento, presenti
nella soluzione. Il Terzo Principio della Dinamica prevede che esista una forza uguale e
contraria esercitata dagli ioni in movimento sulla calamita stessa. L’esperimento precedente non è in grado di rilevarla in quanto la calamita è solidalmente fissata all’apparato
sperimentale. Tuttavia se la calamita fosse libera di muoversi, essa lo farebbe, proprio a
causa di questa forza. Da tali considerazioni nasce la nostra idea della “Barchetta Magnetica”.
15
Premio Cesare Bonacini 2003
ESPERIENZA:
OBIETTIVO:
MATERIALI:
LA BARCHETTA MAGNETICA
STUDIO DELL’INTERAZIONE TRA COMPO MAGNETICO E CORRENTE ELETTRICA, MANTENENDO LA
SOLUZIONE FERMA E LASCIANDO LIBERE DI MUOVERSI LE CALAMITE POSTE SUL FONDO DI UNA
BARCHETTA DI POLISTIROLO.
AMPEROMETRO, VOLTMETRO, 4 COPPIE DI ELETTRODI DI RAME (20 X 100 MM), CAVETTI DI
COLLEGAMENTO, GENERATORE DI TENSIONE, 4 DEVIATORI, VASCA DI PLASTICA, SOLUZIONE
DI Cu SO4 (CONC. 1M), 2 MAGNETI MODELLO N35, BARCHETTA DI POLISTIROLO, CRONOMETRO,
METRO.
Questa esperienza consiste nello studio della situazione inversa rispetto a quella
studiata precedentemente. Ossia nello studio del movimento di “una calamita” (la
barchetta magnetica) a causa di una corrente elettrica, in un liquido praticamente
fermo.
La progettazione e realizzazione dell’apparecchiatura riprodotta nella Foto 12, è il
risultato finale di vari tentativi spesso infruttuosi che ci hanno impegnato per un
tempo
piuttosto
lungo
durante
quest’anno scolastico. La “vasca” ha
svolto la funzione di canale di navigazione per la nostra barchetta ed è stata
realizzata con l’impiego di una canalina
di plastica quadrata che di solito viene
usata per l’alloggiamento dei cavi elettrici. Con l’aiuto del tecnico di laboratorio
abbiamo opportunamente tagliato e sigillato i vari pezzi e li abbiamo fissati su
un piano di compensato2.
Foto 12
Foto 13
Per eseguire questo esperimento è stato
Particolare della barchetta
inoltre necessario fissare due sbarramenti alle estremità del canale per
far si che la soluzione rimanesse quanto più possibile ferma.
All’interno del canale abbiamo posto gli elettrodi, che in una prima fase
dell’esperimento erano soltanto due, lunghi 40 cm ed alti 1cm. L’impiego di
due soli elettrodi di queste dimensioni non ci ha permesso però di raggiungere densità di correnti sufficientemente elevate da muovere la barchetta, in
quanto i nostri alimentatori erano limitati ad un massimo di 3,5A di corrente
(da cui una densità massima di 3,5A/40cm2). In queste situazioni ogni tentativo di far muovere la barca è stato vano. Abbiamo allora deciso di dividere
questo elettrodo in 4 parti più piccole, della lunghezza di 10 cm. ciascuno.
Inoltre abbiamo utilizzato dei deviatori di corrente in modo da alimentare
Foto 14
due coppie di elettrodi alla volta in corrispondenza della posizione della barchetta (come illustrato nello Schema 2). In questa esperienza abbiamo utilizzato una soluzione 1M di CuSO4.
La barchetta infine è stata costruita modellando un pezzetto di polistirolo sul quale sono stati applicati 2 magneti:
uno sopra ed uno sotto la barchetta (vedi Foto 13).
Generatore
Con questa scelta la barchetta si è finalmente mossa
lungo la canalina ed abbiamo potuto misurarne la veloDeviatori
cità in funzione della corrente.
Per evitare influenze di materiali ferromagnetici presenti nei banconi del laboratorio abbiamo sollevato la
Elettrodi
nostra canalina a circa 20cm dal bancone ed abbiamo
accuratamente allontanato tutti gli oggetti metallici. (infatti era sufficiente la presenza di un bullone al bordo
della canalina per mettere in moto la barchetta) Inoltre,
nell’esecuzione dell’esperimento abbiamo mediato ogni
misura di velocità in un percorso di andata e ritorno
(invertendo alla fine dell’andata, il verso della corrente),
in modo da eliminare eventuali influenze esterne (errori
Schema 2
sistematici). Durante l’esperimento si osservava che la
2
La scelta di costruire un “circuito” d’acqua è stata effettuata allo scopo di estendere gli esperimenti riportati in questa relazione, misurando contemporaneamente “azione” e “reazione”, ossia il movimento contemporaneo (ed opposto) dell’acqua e della
barchetta. Purtroppo il tempo a disposizione e le difficoltà incontrate non ci hanno permesso di perfezionare quest’ultima esperienza.
16
Premio Cesare Bonacini 2003
barchetta raggiungeva la velocità di regime dopo 5÷6 cm, pertanto le misure dei tempi di percorrenza sono state effettuate considerando soltanto il tragitto che va dalla seconda alla quarta coppia di elettrodi..
I dati misurati sono raccolti nella tabella sottostante.
DATI MISURATI
Lunghezza percorso (sola andata)
Massa barca
310 mm
5,75 g
Velocità in funzione dell'Intensità di Corrente
1
2
3
4
I (A)
2,0
2,6
3,0
3,6
velocità
(mm/s)
13,7
16,7
19,9
22,7
tempo (s)
22,7
18,5
15,6
13,7
velocità = 6,4857 I
velocità (mm/s)
n
30
25
20
15
10
5
0
0
0,5
1
1,5
2
2,5
3
3,5
I (A)
Dati
incertezze
Figura 9
ANALISI DEI DATI MISURATI
Anche in questo caso si nota una proporzionalità diretta tra la velocità della barchetta e la
corrente elettrica prodotta nella soluzione. Questo andamento mette di nuovo in evidenza
la presenza di forze di attrito di tipo viscoso, a causa delle quali si raggiunge una velocità
massima proporzionale alla forza motrice.
CONCLUSIONI
A questo punto siamo in grado di rispondere ad alcune delle domande che ci eravamo
posti all’inizio di questo lavoro.
1) La calamita esercita una forza sulle particelle cariche in movimento (Pompa Magnetica) e viceversa le particelle cariche in movimento esercitano una forza sulla
calamita (Barchetta Magnetica)
2) Le forze sono effettivamente perpendicolari alla direzione di moto delle cariche
elettriche
Quale sia il meccanismo con cui le cariche elettriche
possono esercitare una forza sulla calamita, lo possiamo
soltanto ipotizzare con il seguente ragionamento.
Torniamo al semplice esperimento qualitativo della calamita posta sopra la superficie della soluzione di CuSO4.
L’acqua acquista un moto perpendicolare alla direzione
della corrente elettrica. In questo moto perpendicolare
sia gli ioni positivi che quelli negativi si muovono lungo
la stessa direzione e con lo stesso verso, ma la presenza
Schema 3
di un campo magnetico li separa spazialmente. Allontanandosi dalla calamita gli ioni si vengono a trovare in una zona in cui il campo magnetico
si annulla e quindi le forze elettriche tra le cariche opposte agiscono in modo da eliminare
la separazione di carica prodotta dal campo magnetico. Questo movimento di cariche è
equivalente ad una spira percorsa da corrente che crea un campo magnetico parallelo a
quello della calamita e dunque una forza di repulsione(Schema 3). Succede lo stesso effetto quando poniamo sul bancone due calamite con la stessa orientazione. Avvicinandole
esse risentono di una forza repulsiva sempre più intensa.
4
Premio Cesare Bonacini 2003
BIBLIOGRAFIA DELLE FONTI UTILIZZATE
•
Antonio Rostagni
FISICA GENERALE VOL. 2
UTET (1978)
•
Ugo Amaldi
LA FISICA PER I LICEI SCIENTIFICI (quarta edizione) VOL. 1
ZANICHELLI 1997
•
Ugo Amaldi
LA FISICA PER I LICEI SCIENTIFICI (quarta edizione) VOL. 3
ZANICHELLI 1999
•
MATERIALI ORIGINALI di nostra produzione e non pubblicati
17