INTERAZIONE RADIAZIONE MATERIA
Per il corso di Fisica Applicata
CdS Biotecnologie
A.A. 2002-2003
Prof. Maria Pia De Pascale
URTI
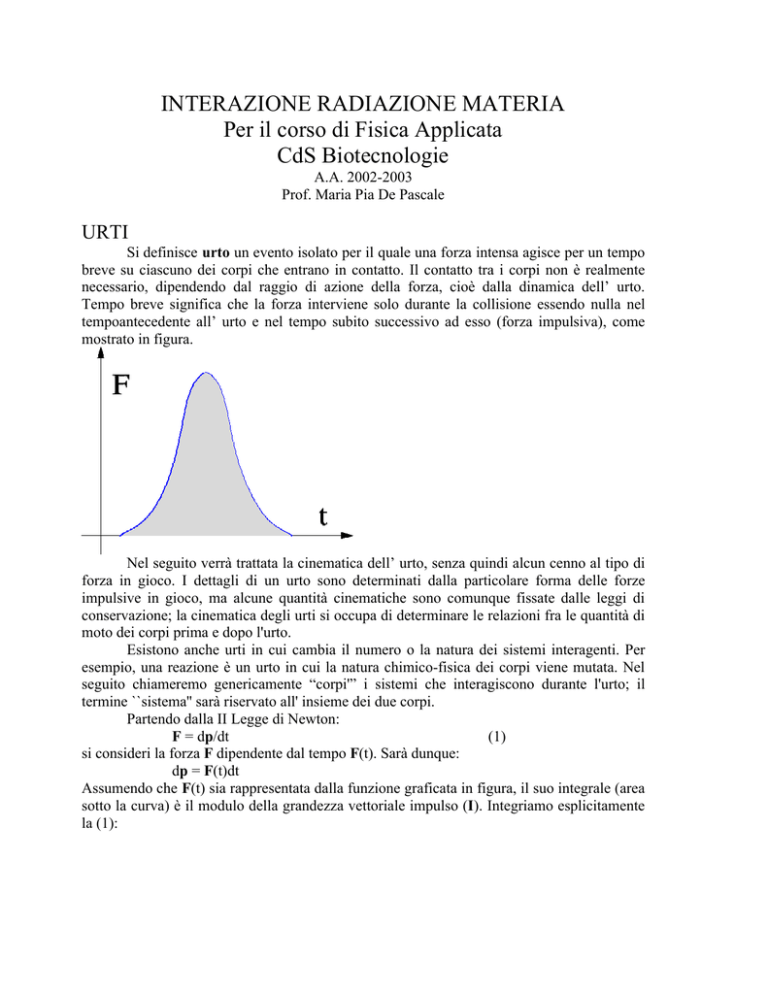
Si definisce urto un evento isolato per il quale una forza intensa agisce per un tempo
breve su ciascuno dei corpi che entrano in contatto. Il contatto tra i corpi non è realmente
necessario, dipendendo dal raggio di azione della forza, cioè dalla dinamica dell’ urto.
Tempo breve significa che la forza interviene solo durante la collisione essendo nulla nel
tempoantecedente all’ urto e nel tempo subito successivo ad esso (forza impulsiva), come
mostrato in figura.
Nel seguito verrà trattata la cinematica dell’ urto, senza quindi alcun cenno al tipo di
forza in gioco. I dettagli di un urto sono determinati dalla particolare forma delle forze
impulsive in gioco, ma alcune quantità cinematiche sono comunque fissate dalle leggi di
conservazione; la cinematica degli urti si occupa di determinare le relazioni fra le quantità di
moto dei corpi prima e dopo l'urto.
Esistono anche urti in cui cambia il numero o la natura dei sistemi interagenti. Per
esempio, una reazione è un urto in cui la natura chimico-fisica dei corpi viene mutata. Nel
seguito chiameremo genericamente “corpi'” i sistemi che interagiscono durante l'urto; il
termine ``sistema'' sarà riservato all' insieme dei due corpi.
Partendo dalla II Legge di Newton:
F = dp/dt
(1)
si consideri la forza F dipendente dal tempo F(t). Sarà dunque:
dp = F(t)dt
Assumendo che F(t) sia rappresentata dalla funzione graficata in figura, il suo integrale (area
sotto la curva) è il modulo della grandezza vettoriale impulso (I). Integriamo esplicitamente
la (1):
pf
tf
pi
ti
∫ dp = ∫ F(t )dt
che si può riscrivere:
∆p = I
teorema dell’ impulso.
Siccome le forze esterne agenti su di un corpo sono piccole rispetto alla forza media
di un urto, e la forza d'urto è una forza interna, la quantità di moto del sistema dei due corpi
con buona approssimazione si conserva durante l'urto (questa è una riformulazione dell'
approssimazione d'impulso). Nell'intervallo di tempo ∆t pure lo spostamento dei corpi può
essere trascurato.
URTI ELASTICI. Si definisce elastico un urto per il quale è nulla la variazione dell’ energia
cinetica del sistema.
Urti elastici in una dimensione
Consideriamo il caso di un urto perfettamente elastico ed unidimensionale, ovvero due
particelle di massa m1 e m2, con velocità v1e v2 prima dell'urto e v1fe v2f dopo. La
conservazione della quantità di moto e dell'energia cinetica implicano:
m1v1 + m2 v2 = m1v1 f + m2 v2 f
1
1
1
1
m1v12 + m2 v22 = m1v12f + m2 v22 f
2
2
2
2
Sviluppando il sistema e sostituendo la differenza di due quadrati con la formula
A2 − B 2 = (A + B )(A − B ), otteniamo:
m1 (v1 − v1 f )= m2 (v2 − v2 f )
m1 (v1 − v1 f )(v1 + v1 f )= m2 (v2 − v2 f )(v21 − v2 f )
(1)
Semplificando nella seconda relazione le quantità che sono uguali secondo la prima
relazione, otteniamo quindi che:
v1 + v1 f = v2 + v2 f ⇒ v2 f = v1 − v2 + v1 f
(2)
Utilizzando la (2) possiamo ridurci ad una sola variabile, eliminando v2f, per esempio nella
prima relazione di (1):
m1 (v1 − v1 f )= −m2 (v2 − v1 + v2 − v1 f )⇒ (m1 − m2 )v1 + 2m2 v2 = ( m1 + m2 )v1 f
⇒ v1 f =
m1 − m2
2m2
v1 +
v2
M
M
Utilizzando poi la relazione (2) otteniamo con passaggi simili anche l'espressione di v2f.
Riassumendo i risultati:
v1 f =
m1 − m2
2m2
v1 +
v2 ,
M
M
v2 f =
2m1
m − m1
v1 + 2
v1
M
M
Esaminiamo ora alcuni casi particolari derivanti dalle equazioni precedenti. Quando le masse
2m1 2m2
sono uguali i termini (m1-m2)sono nulli e
=
=1, per cui le velocità delle particelle si
M
M
scambiano.
Nel caso poi che v 2=0, la prima particella si ferma e la seconda parte con velocità uguale alla
prima:
m1 = m2 ⇒ v1 f = v2 , v2 f = v1
Se le masse sono diverse e v2=0 allora rimangono solo i termini proporzionali a v1:
m1 ≠ m2 e v2=0
⇒ v1 f =
m1 − m2
2m1
v1 ; v2 f =
v1
M
M
Se la massa del primo corpo è molto maggiore di quella del secondo corpo, M ≈ m1 >> m2 ,
allora v1f ≈v1 e v2f ≈2v1. Se siamo nel limite opposto, m1<<m2≈ M , allora v1f ≈ -v1 e v2f<<v1.
Vediamo un'applicazione di queste conclusioni. Nei reattori nucleari i neutroni prodotti dalla
fissione si muovono molto velocemente; affinchè possano produrre altre fissioni occorre
rallentarli. Nell'ipotesi che i neutroni urtino elasticamente contro i nuclei fermi, i materiali
più adatti per rallentarli sono atomi leggeri di massa vicina a quella del neutrone stesso.
Quindi, sulla base della conservazione della quantità di moto, i moderatori per neutroni
dovrebbero essere costituiti da atomi leggeri.
Urti elastici in due dimensioni
Se l'urto è elastico ma non unidimensionale, le leggi di conservazione non bastano a
determinare il moto dei corpi dopo di esso basandosi solo sulla conoscenza del moto prima
dell'urto. Infatti le uniche equazioni che possiamo scrivere sono:
r
r
r
r
m1 v 1 + m2 v2 = m1v1 f + m2 v2 f
1
1
1
1
m1v12 + m2 v22 = m1v12f + m2 v22 f
2
2
2
2
La prima equazione è vettoriale, quindi conta come tante equazioni scalari quante sono le
r
dimensioni del sistema. Nel caso di urto bidimensionale, note le quantità iniziali v1 ( v1 x , v1 y )
r
r
r
e v2 ( v2 x , v2 y ) rimangono le quattro incognite v1 f ( v1 fx , v1 fy ) e v2 f ( v2 fx , v2 fy ) .
Consideriamo ora il caso di un urto bidimensionale fra due particelle di cui una è
inizialmente ferma. Questo non è affatto un caso restrittivo in quanto si può sempre scegliere
un sistema di riferimento rispetto al quale una delle due particelle risulti ferma prima
dell'urto.
La distanza b fra la direzione del corpo incidente ed una retta ad essa parallela passante per il
corpo fermo viene detta parametro d 'urto. È una misura di quanto direttamente il proiettile
incida sul bersaglio. Per b=0 si ha un urto frontale. Scriviamo per esteso le leggi di
r
r
conservazione, utilizzando gli angoli θ1 e θ2 per determinare le componenti di v 1 e v 2 .
m1 v 1 = m1v1 f cos
0 = m1v1 f sin
1
1
+ m2 v2 f cos
+ m2 v2 f sin
2
2
1
1
1
1
m1v12 + m2 v22 = m1v12f + m2 v22 f
2
2
2
2
Quindi abbiamo quattro quantità incognite, v1f ,v 2f, θ1 e θ2 e tre quantità note m1, m2 e v 1. Si
hanno così quattro incognite per tre equazioni scalari, serve quindi un’ ulteriore
informazione. Se non si conosce il tipo di interazione la quarta informazione necessaria per
risolvere il problema la si deve dedurre dall'esperimento. Tipicamente si misura l'angolo di
deviazione delle due particelle. Ovviamente, al crescere del numero delle dimensioni
servono sempre più quantità misurate.
IL NUCLEO ATOMICO
Le scoperte dell’ elettrone e della radioattività naturale hanne segnato l’ inizio di una
nuova era nello studio della struttura della materia. Alcuni indizi indicavano chiaramente il
fatto che la materia dovesse essere costituita da atomi: ad esempio, i rapporti stechiometrici
in chimica, la termodinamica dei gas, il sistema periodico degli elementi. Il problema era la
mancanza di un modello che permettsse di “costruire” gli atomi.
Le scoperte della fine dell’ 800 mostrarono per la prima volta l’ esistenza di
“particelle” emergenti dalla materia, che dunque dovevano essere interpretate come suoi
costituenti. Queste particelle, prodotte nei processi radioattivi, furono utilizzate per
bombardare altri elementi al fine di studiarne i costituenti. Questo è un postulato
sperimentale che è alla base della fisica moderna nucleare e delle particelle. Studi sistematici
divennero possibili negli anni ’30 grazie all’ utilizzazione dei primi acceleratori di particelle.
Già prima erano stati scoperti i costituenti fondamentali degli atomi: l’ elettrone, il protone, il
neutrone.
L’ elettrone fu il primo costituente dell’ atomo ad essere scoperto. Nel 1897 J.J.
Thomson fu in grado di produrre fasci di elettroni all’ interno di tubi a vuoto. Dalla misura
delle deflessione da essi subita sotto l’ azione combinata di campi elettrici e magnetici, egli
potè misurarne la velocità e dedurre il rapporto tra la massa e la carica della particella. In
seguito, riuscì a determinare la carica dell’ elettrone (per definizione data negativa),
utilizzando un metodo, poi migliorato da Millikan nel 1910.
Nei primi anni del Novecento, vennero proposti diversi modelli atomici. Il modello di
Thompson (1907) descriveva l’ atomo come un insieme di cariche negative e posistive
uniformemente distribuite nel volume atomico, cosicchè l’ atomo risulta globalmente neutro.
L’ esperienza di Rutherford, Geiger e Marsden, descritta nel successivo paragrafo,
mise in evidenza l’ inconsistenza di questo modello. Rutherford bombardò con particelle alfa
(nuclei di He) anche nuclei leggeri. Osservando i risultati del bombardamento dell’ azoto,
notò che venivano prodotte particelle cariche posistivamente, in grado di percorrere distanze
lunghe e che dovevano provenire dall’ atomo stesso. Simili particelle le aveva già osservate
in esperimenti che avevano l’ idrogeno come bersaglio. Da questo concluse che le particelle
osservate erano nuclei di idrogeno, presenti allo stesso modo nei nuclei di azoto.
Anche il neutrone venne scoperto nello stesso modo: bombardando nuclei con
particelle alfa. Essendo neutre, queste particelle non potevano essere osservate in modo
diretto; Chadwick mise a punto un metodo sperimentale per farlo, misurando le energie di
rinculo dei nuclei dei bersagli di idrogeno, elio e azoto, soggetti all’ urto della radiazione
neutra prodotta da un bersaglio di berillio bombardato con particelle alfa. Usando la
cinematica dell’ urto, fu in grado di stabilire che la massa delle particelle costituenti la
radiazione neutra era molto simile a quella del protone e coniò il nome neutrone.
Esperienza di Rutherford.
Nel laboratorio di Rutherford, Geiger e Marsden eseguirono esperimenti per studiare la
diffusione di particelle alfa su strati sottili metallici. Nel 1909 osservarono che le particelle
alfa, ottenute nel decadimento radioattivo, occasionalmente diffondono ad angoli superiori a
900, risultato fisicamente impossibile a meno che esse non urtino su bersagli di massa molto
superiore alla massa delle particelle alfa stesse. In base al modello atomico di Thompson,
tutte le alfa si sarebbero dovute trovare ad angoli piccoli rispetto all’ asse del fascio
incidente, ma in piccola percentuale, alcune vengono diffuse ad angoli fino a 1400 .
Fig. 1 Descrizione dell’ esperimento.
Questo esperimento ha dunque mostrato che la carica positiva di un atomo è concentrata in
un volume molto piccolo ed è pertanto alla base delle nostre attuali conoscenze sul nucleo
atomico.
La diffusione delle particelle alfa su nuclei può essere spiegata a partire dalla forza di
Coulomb e trattata in prima approssimazione come un urto elastico. Infatti, la forza
coulombiana, repulsiva in questo caso, impedisce che vi sia contatto fra il proiettile e il
bersaglio.
Fig. 2 Geometria della diffusione Rutherford.
Come mostrato in figura 2, la trattazione cinematica è quella di un urto elastico, non frontale,
bidimensionale, già trattata nel capitolo precedente. La misura sperimentale degli angoli di
deflessione delle particelle alfa, usata come parametro nelle equazioni descritte, permette di
calcolare la massa, incognita, del bersaglio.
Il nucleo atomico
I nuclei atomici sono formati da protoni1 e neutroni (nucleoni), legati insieme dall’
interazione nucleare (o interazione forte). Il nome “forte” viene utilizzato proprio perchè
questa forza risulta essere molto più intensa di quella elettromagnetica. Per spezzare il
legame che tiene insieme un nucleo, infatti, c’è bisogno di una grande quantità di energia,
come dimostra il fatto che bisogna bombardarli con particelle alfa.
Un nucleo contiene A nucleoni (A= numero di massa), di cui Z (numero atomico) è il
numero di protoni (la carica del nucleo è quindi Q=Ze)2 e N = A-Z neutroni. Combinazioni
differenti di Z e N sono dette nuclidi. Nuclidi con lo stesso numero di massa, A, sono detti
isobari, con lo stesso numero atomico, Z, sono detti isotopi, con lo stesso numero di
neutroni, N, sono detti isotoni.
In Fig.3 è mostrata la carta dei nuclidi. Nel grafico si riporta la posizione di un nuclide di dati
Z e N.
Fig.3 Carta dei nuclidi.
1
La massa del protone è pari a 1.67262158 10-27 kg = 938.272 MeV/c2 = 1836.149 me, quella del neutrone è
pari a 1.67492716 10-27 kg = 939.565 MeV/c2 = 1838.679 me
2
La carica elementare, e, è pari a 1.6 10-19 C. Gli atomi sono elettricamente neutri, il che dimostra l’
uguaglianza fra il valore assoluto della carica elettrica positiva del protone e quella negativa dell’ elettrone.
Le rette con pendenza negativa sono relative al numero di massa A. Si noti come, all’
aumentare di A, i nuclidi si dispongono in una zona che si allontana sempre più dalla
bisettrice del quadrante, ovvero la retta per la quale N=Z. Dallo studio del grafico possiamo
quindi evincere alcuni fatti sperimentali:
1. Esiste un limite massimo di nucleoni che possono costituire il nucleo (A≈260).
2. Non esistono nuclei formati da soli protoni (oltre l’ idrogeno), nè da soli neutroni.
3. All’ aumentare di A, sono preferiti nuclei con un maggior numero di neutroni rispetto
ai protoni.
E’ possibile, con apposita strumentazione, determinare sperimentalmente la massa dei nuclei.
Si nota che la massa totale di un nucleo è minore della somma delle masse dei singoli
costituenti, ovvero:
M < Zmp+Nmn
Questa differenza in massa è la misura dell’ energia necessaria a mantenere il nucleo legato
(energia di legame) e che può essere calcolata a partire dalla relazione di Einstein3:
E=mc2
Dunque.∆M = (Zmp + Nmn) –M(A,Z) = Elegame (in unità in cui c=1).
Precisiamo inoltre che, essendo legata ad una differenza di massa, quindi di energia, l’
energia di legame è una quantità negativa.
Vogliamo notare esplicitamente che la formula data per l’ energia di legame è un’
espressione di carattere del tutto generale, ovvero indipendente dall’ interazione (o forza),
valida pertanto per qualsiasi sistema di particelle interagenti. L’ intensità della forza
(gravitazionale, elettromagnetica, debole o nucleare) ed il suo raggio di azione determinano
però il valore dell’ energia di legame del sistema. Per esempio:
Sistema Terra-Sole (interazione gravitazionale) ∆M/M = 10-14
Cristallo (interazione elettromagnetica) ∆M/M = 10-11
Reazioni chimiche (interazione elettromagnetica) ∆M/M = 10-8
Nuclei (interazione forte) ∆M/M = 10-2
Possiamo introdurre la quantità B=–E(A,Z)/A, ossia energia di legame per nucleone. In
Figura 4 è riportato l’ andamento di B in funzione di A. L’ esame del grafico suggerisce
alcune conclusioni:
1. Escludendo i nuclei con A<20, l’ andamento della funzione è circa costante intorno
ad un valore medio dell’ ordine di 8 MeV/nucleone.
2. il Ferro è l’ elemento cui corrisponde il massimo valore della curva.
3
La ben nota relazione massa-energia di Einstein include sia l’ energia cinetica di una particella, sia l’ energia
che essa ha per il fatto che possiede una massa. Detta m0 la massa a riposo della particella, ovvero la massa di
una particella ferma o che si muove a velocità molto inferiori a quella della luce, c, E0= m 0c2 è la sua energia a
riposo.
3. per nuclei di basso A sono possibili le reazioni di fusione4
4. per nuclei di alto A sono possibili le reazioni di fissione5.
Interpretiamo quindi tutte le indicazioni che abbiamo fin qui raccolto per ottenere le
caratteristiche dell’ interazione nucleare. Possiamo affermare che:
Fig. 4 Energia di legame per nucleone, in funzione del numero di massa A.
1. l’ intensità della forza è molti ordini di grandezza superiore rispetto alle interazioni
gravitazionale e elettromagnetica, come si vede dal confronto della frazione di massa
trasformata in energia di legame e dal fatto che nuclei con più protoni sono
comunque legati, nonostante l’ azione repulsiva della forza coulombiana;
2. il raggio di azione della forza deve essere breve, come dimostrato dall’ andamento
grossolanamente lineare della curva. Infatti, se il raggio di azione fosse lungo (come
nel caso gravitazionale ed elettrostatico, in cui la forza è inversamente proporzionale
al quadrato della distanza), la curva dovrebbe presentare un andamento quadratico;
inoltre, potrebbero esistere nuclei con numero di massa maggiore di 260;
4
La fusione nucleare è un processo che coinvolge i nuclei di più atomi, nel momento in cui ciascun nucleo,
dotato di sufficiente energia cinetica per superare la reciproca repulsione (causata dalla carica elettrica
positiva), viene catturato dalla forza nucleare forte degli altri nuclei e si combina con questi, formando un
nucleo più pesante, la cui massa è leggermente inferiore alla massa complessiva dei nuclei originari. La
differenza in massa è convertita in energia. L’ energia prodotta nelle stelle proviene da questo processo.
5
La fissione nucleare consiste in un processo per cui il nucleo pesante, di uranio, torio o plutonio, colpito da un
neutrone, si spezza in due parti, liberando nel contempo una grande quantità di energia.
3. la forza nucleare deve essere indipendente dalla carica elettrica, agendo allo stesso
modo sui protoni e sui neutroni.
Abbiamo dunque, in prima approssimazione:
B∝A, ossia: B= - b0A +correzioni
Le correzioni da introdurre, come abbiamo in parte già visto, sono:
1. termine di correzione di superficie, dovuto al fatto che i nucleoni sulla superficie nel
nucleo (modellizzato in questo caso come fosse una goccia liquida), sono meno legati
dei nucleoni interni. Questo termine è quindi slegante (positivo) e tiene conto dell’
effetto di “tensione superficiale”;
2. termine di correzione coulombiano, dovuto alla presenza nel volume del nucleo di
cariche positive (protoni) che sono soggette all’ azione repulsiva della forza elettrica;
3. termine di asimmetria, di tipo quantistico, legato al principio di esclusione di Pauli.
Se immaginiamo il nucleo come un insieme di livelli energetici per ognuno dei quali
è possibile inserire un solo protone e un solo neutrone, quando il numero di neutroni
aumenta (caso dei nuclei pesanti), questi devono sistemarsi in livelli energetici
sempre più alti. L’ energia di legame deve quindi essere più bassa di quella di un
ipotetico nucleo, di pari A, in cui metà dei neutroni in eccesso è trasformata in
protoni (ognuno dei quali può condividere lo stesso livello energetico di un
neutrone). Questo termine è pertanto proporzionale alla quantità (N-Z)/2.
4. Il numero di massa A può essere pari o dispari. Abbiamo 167 nuclei stabili con A
pari e 103 con A dispari. Nel primo caso (A pari) 163 con N e Z entrambi pari e solo
4 con N e Z dispari. Nel secondo caso (A dispari) sono circa in ugal numero i casi Z
pari, N dispari e viceversa. L’ ultimo termine correttivo tiene dunque conto della
preferenza per i nuclei Z pari- N pari.
La formula che si ottiene, detta formula semiempirica dell’ energia di legame o formula di
von Weizsäcker è la seguente:
2
3
E ( Z , A) = −b0 A + b1 A + b2
Z2
1
3
+ b3
(N − Z )2
A
±
A
dove il segno di δ è positivo per i nuclei dispari-dispari, negativo per i nuclei pari-pari, nullo
per gli altri nuclei.
I valori generalmente usati per quasi tutti i nuclei dei coefficienti sono: b0= 14.1 MeV, b 1=13
MeV, b2 = 0.595 MeV, b3=19 MeV, δ = 33.3/(A)3/4 MeV.
In Figura 5 sono riportati gli andamenti dei vari contributi esaminati all’ energia di legame.
Fig. 5. Contributi dei vari effetti all’ energia di legame per nucleone
La formula dell’ energia di legame si basa su alcune delle proprietà tipiche di una
goccia di liquido: densità costante, forze a piccolo raggio di azione, saturazione,
deformazione e tensione superficiale, pertanto il modello nucleare da essa descritto prende il
nome di modello a goccia.
I nuclei stabili si trovano (Fig. 3) lungo una stretta fascia nel piano Z-N. Tutti gli altri
sono instabili e decadono spontaneamente. I decadimenti sono legati a considerazioni
energetiche: i nuclei si portano in uno stato in cui l’ energia è minima. Questo può avvenire
in vari modi: per gli isobari con eccesso di neutroni, è energeticamente vantaggioso
convertire un neutrone in un protone, mentre nel caso di eccesso di protoni può essere
vantaggiosa la reazione inversa (decadimento beta). I nuclei di Fe e Ni posseggono la
massima energia di legame, sono pertanto i nuclidi più stabili6. Nei nuclei più pesanti, a
causa della maggiore repulsione coulombiana, l’ energia di legame è minore. I nuclei ancora
più pesanti diventano instabili e decadono per fissione in due o più nuclei di massa inferiore.
Perchè questo si verifichi, la massa dell’ atomo originario deve essere superiore alla somma
delle masse dei prodotti finali del processo. Quando un nucleo pesante decade
spontaneamente in due nuclei massivi, si parla di fissione spontanea.
6
Un isotopo è considerato stabile se la sua vita media è considerevolente più lunga della vita del sistema solare.
DECADIMENTI NUCLEARI
Decadimento alfa. Sono detti particelle alfa i nuclei di 4He emessi nel decadimento di nuclei
radioattivi (per esempio, 230Th → 226Ra). Protoni e neutroni hanno, anche nei nuclei più
pesanti, un’ energia di legame media di circa 8 MeV, il che fa sì che essi normalmente siano
confinati nel nucleo. In molti casi, però si verifica che l’ emissione di un gruppo di nucleoni,
sotto forma di sistema legato, sia energeticamente favorita, dal momento che l’ energia di
legame di questo gruppo sistema accresce l’ energia totale disponibile per il processo. La
probabilità che un tale sistema si formi all’ interno del nucleo diminuisce con l’ aumentare
dei nucleoni coinvolti nel processo. Il caso più importante è quello che avviene con l’
emissione del nucleo di 4He, cioè di un sistema legato di due protoni e due neutroni. A
differenza del caso di 2 o 3 nucleoni, questo sistema è molto compatto (energia di legame di
circa 7 MeV/nucleone). La particella alfa che si forma all’ interno del nucleo è soggetta a due
tipi di forze: a piccole distanze dal centro, prevale l’ interazione forte, attrattiva, a più grandi
distanze essa è soggetta all’ azione repulsiva della forza coulombiana. A distanze maggiori
del raggio nucleare, l’ unica forza attiva è quella coulombiana. La radiaottività alfa naturale
si presenta nelle famiglie radioattive naturali, per nuclei con Z>82 e A≥200.
Decadimento beta. La scoperta di elettroni emessi da alcune specie nucleari (emissione
beta) è storicamente contemporanea a quella del decadimento alfa. Tuttavia l’ interpretazione
corretta del meccanismo di questo decadimento ha richiesto un tempo molto lungo, essendo
la manifestazione dell’ esistenza dell’ interazione debole, la quarta interazione fondamentale
(le altre, ricordiamo, sono: gravitazionale, elettromagnetica e forte). L’ interpretazione
corretta dei decadimenti alfa e gamma discende dall’ osservazione della transizione (o
decadimento) di un nucleo ad un certo stato di un altro nucleo, con uno spettro discontinuo
delle emissioni che rispecchia la conservazione dell’ energia nei vari stadi del processo. Al
contrario, la distribuzione dell’ energia degli elettroni emessi nel decadimento beta è
continua. La curva di energia che si ottiene ha un valore medio che è minore dell’ energia
massima che un elettrone può avere. Questa caratteristica, una volta esclusa la possibilità che
gli elettroni possano perdere energia uscendo dal nucleo, è spiegata dalla presenza di un’
altra particella, neutra e non rivelabile, che viene emessa contemporaneamente all’ elettrone.
A questa particella Fermi diede il nome di neutrino. La reazione è dunque del tipo:
Y → Z −1AX + e − +
A
Z
e
che corrisponde al processo elementare per il quale un neutrone si trasforma in un protone:
n → p + e− +
e
Decadimento gamma. I nuclei hanno di solito molti stati eccitati. La maggior parte degli
stati ad energia più bassa sono teoricamente ben spiegati. Di solito gli stati eccitati più bassi
decadono emettendo radiazione elettromagnetica (fotoni). Se esistono stati la cui energia di
eccitazione è superiore all’ energia di legame di un singolo nucleone (circa 8 MeV), nel
processo di diseccitazione si può verificare la cessione di energia al nucleone e la
conseguente emissione di esso al di fuori del nucleo. Di solito, vengono emessi con questo
meccanismo neutroni, che non risentono della barriera coulombiana.
INTERAZIONI DELLA RADIAZIONE CON LA MATERIA - 1
Radiazione neutra: fotoni. La caratteristica peculiare dell’ interazione di un fascio di fotoni
con la materia è che esso non viene degradato in energia, ma solo attenuato in intensità. Nell’
attraversare uno spessore di materiale, quindi, vi è una probabilità che un singolo fotone del
fascio interagisca, diminuendo così il numero (intensità) dei fotoni del fascio uscente. Questo
dipende dalla natura dei processi di interazione possibili. Essi sono:
Effetto fotoelettrico
Effetto Compton
Produzione di coppie.
L’ attenuazione del fascio di fotoni è descritta da un’ esponenziale, in funzione dello
spessore x attraversato e dalle caratteristiche del materiale stesso, riassunte nel coefficiente
di assorbimento µ:
I ( x) = I 0e −
x
dove I0 è l’ intensità del fascio incidente.
Effetto fotoelettrico. Si tratta dell’ assorbimento di un fotone da parte di un elettrone atomico
con la successiva emissione dell’ elettrone dall’ atomo. Poichè un elettrone libero non può
assorbire un fotone senza violare il principio di conservazione della quantità di moto, è
necessario che l’ elettrone sia legato al nucleo atomico, che, rinculando, assicura che il
principio di conservazione tenga. L’ energia dell’ elettrone emesso è Ee=hν - Eleg, dove hν è
l’energia del fotone incidente e Eleg è l’ energia di legame dell’ elettrone. L’ energia del
fotone incidente, pertanto, deve essere confrontabile con l’ energia di legame degli elettroni,
dell’ ordine del centinaio di keV.
Effetto Compton. Questo effetto diviene evidente quando l’ energia del fotone è molto
maggiore dell’ energia di legame degli elettroni (da qualche centinaio di keV a pochi MeV).
In questo caso, l’ elettrone può essere trattato come una particella libera (cioè non legato all’
atomo). Si può schematizzare l’ effetto come una diffusione (urto) tra un proiettile (il fotone)
e un bersaglio massivo (l’ elettrone). La cinematica dell’ urto è mostrata in figura.
Applicando quindi le leggi di conservazione del’ energia e della quantità di moto1, come già
visto, si possono ricavare le energie dell’ elettrone e del fotone diffuso, in funzione degli
angoli di emissione e dell’ energia del fotone incidente. Anche qui, l’ urto è elastico ed in
due dimensioni.
1
Per un fotone, l’ espressione classica della quantità di moto non può essere applicata. Si può però ottenere a
partire dall’ espressione generale dell’ energia E
pari a zero. Si ha quindi
p=
E h
h
=
= .
c
c
= mc 2 =
p 2 c 2 + m02 c 4 , ponendo la massa a riposo, m0,
Produzione di coppie. Il processo di produzione di coppie comporta la trasformazione di un
fotone in una coppia elettrone-positrone. Perchè si conservi la quantità di moto è necessario
che ciò avvenga in presenza di un nucleo. Questa reazione ha inoltre una soglia in energia,
pari alla somma delle masse delle particelle che vengono prodotte, ossia 2 volte la massa
dell’ elettrone, circa 1.022 MeV.
Il processo di produzione di coppie è strettamente correlato a quello di
bremsstrahlung, ovvero l’ emissione di onde elettromagnetiche da parte di un elettrone (o di
un positrone) che interagisce con il campo elettrico di un nucleo. Classicamente il processo
di bremsstrahlung si spiega considerando la radiazione emessa dall’ elettrone quando viene
accelerato dal campo elettrico del nucleo; l’ elettrone cambia quindi la sua traiettoria.
Il risultato dell’ effetto combinato della produzione di coppie da parte di fotoni di alta
energia e dell’ emissione per bremsstrahlung degli elettroni è la formazione degli sciami
elettrofotonici. Un fotone di alta energia nella materia converte in una coppia elettrone
positrone; a loro volta essi emettono un fotone di bremssatrhlung ciascuno. Ogni fotone così
prodotto può di nuovo convertire in una coppia. La sequenza si ripete finchè l’energia
disponibile non è inferiore all’ energia di soglia per la produzione di coppie.
Lo sviluppo dello sciame è naturalmente un processo statistico. E’ possibile costruire
un modello semplice per ottenere il numero di particelle prodotte e le loro energie medie in
funzione della profondità di penetrazione all’ interno del materiale. E’ necessario, per far ciò,
introdurre il concetto di lunghezza di radiazione: essa è definita come la distanza percorsa in
un dato materiale da un elettrone lungo la quale l’ elettrone riduce la sua energia di 1/e.
Supponiamo di iniziare da un fotone di energia E0. In media, il fotone convertirà in
una coppia elettronica dopo una lunghezza di radiazione. L’ energia di ogni membro della
coppia è dunque E0/2. Dopo due lunghezze di radiazione l’ elettrone e il positrone
emetteranno un fotone di bremsstrahlung di energia pari alla metà di quella delle particelle.
Avremo ora 4 particelle: due fotoni e due particelle cariche di energia E0/4. Dopo tre
lunghezze di radiazione, i due fotoni di bremsstrahlung avranno formato una coppia ognuno,
mentre le due particelle originarie avranno emesso ciascuna un fotone di bremsstrahlung. Il
numero di particelle è ora 8 con un’ energia pari a E0/8. Per cui, dopo t lunghezze di
radiazione il numero di particelle presenti sarà N=2t con un’ energia media E(t)=E0/2t. Allo
stesso risultato si perviene se la particella iniziale è un elettrone invece del fotone. Tenendo
conto che i processi di produzione di coppie e di bremsstralung si arrestano all’ energia
critica E c=1.022 MeV, la massima profondità dello sciame si ottiene: E(tmax) = E 0/2tmax = E c,
E
ln 0
Ec
che, risolta per tmax, ci dà: t max =
. Il numero di particelle sarà Nmax=E0/Ec.
ln 2
Nello sviluppo dello sciame, le sue dimensioni laterali aumentano per vari processi.
Innanzitutto, la cinematica ci dice quale è l’ angolo tra le direzioni dell’ elettrone e del
positrone nel processo di produzione di coppie (cinematica di un urto elestico
bidimensionale): le due particelle avranno direzioni diverse da quella del fotone incidente.
Inoltre vi sono altri effetti che allontanano le particelle dall’ asse longitudinale, quali la
diffusione multipla e l’ emissione dei fotoni di bremsstrahlung. Nel complesso, quindi, nel
propagarsi attraverso il materiale, lo sciame sarà geometricamente contenuto in un volume
conico, il cui vertice è nel punto di impatto del fotone (o elettrone) iniziale e il cui raggio di
base, valutato nel punto di massimo sviluppo, si misura in termini di raggio di Moliere. Con
E
questa notazione si indica la quantità RM = Lrad s , dove Lrad è la lunghezza di radiazione
Ec
= 21.2 MeV . Questa notazione contiene le caratteristiche del
nel materiale, E s = me c 2 4
materiale e pertanto è di utilizzo generale.
Radiazione neutra: neutroni. Come i fotoni, anche i neutroni hanno carica elettrica nulla.
Dunque, anche essi non sono soggetti alle interazioni coulombiane con gli elettroni e i nuclei
del materiale. I neutroni interagiscono con i nuclei grazie alla forza nucleare forte, che è il
processo principale. Naturalmente, visto che il raggio di azione della forza forte è molto
piccolo, le interazioni dei neutroni sono un processo raro: essi devono avvicinarsi al nucleo
ad una distanza di circa 10-13 cm, perchè possa avvenire una reazione. Pertanto i neutroni
sono particelle molto penetranti. Quando il neutrone interagisce, può dar luogo a processi
diversi, che dipendono dall’ energia del neutrone incidente. Per esempio:
Neutroni energetici (> qualche MeV). Urtano elasticamente sul nucleo. La reazione è del tipo
A+n→A+n. Il neutrone nell’ urto cede parte della sua energia al nucleo, che rincula.
Neutroni di energia superiore a 1 MeV possono urtare anelasticamente sul nucleo, che dopo
l’ urto si trova in uno stato eccitato: A+n→A*+n. Successivamente il nucleo eccitato può
ritornare allo stato fondamentale per emissione elettromagnetica.
Cattura radiativa. Il neutrone penetra all’ interno del nucleo e vi rimane come costituente
(urto totalmente anelastico).Il processo è accompagnato dell’ emissione di energia
elettromagnetica (fotone). La reazione è del tipo X(Z,N) +n→X(Z,N+1) + γ. Questa reazione
avviene con probabilità inversamente proporzionale alla velocità del neutrone, pertanto a
basse energie.
Fissione indotta. Anche questa, come la cattura radiativa, avviene per energie del neutrone
molto basse (dell’ ordine della frazione di eV). Siccome l’ energia del neutrone è
confrantabile con l’ energia di agitazione termica a temperatura ambiente, i neutroni sono
detti termici. Nel processo di fissione, il neutrone viene catturato dal nucleo, che diviene
instabile. L’ instabilità provoca la deformazione del nucleo che, da una simmetria
grossolanamente sferica, diventa bilobato. A questo punto, entrano in contrasto la forza forte
nucleare e la forza elettrostatica. La prima, essendo a corto raggio, si esercita solo nella
strozzatura fra i due lobi ed è attrattiva; la seconda, repulsiva, si esercita fra le cariche
positive dei lobi. Se la deformazione è tale da rendere piccola la strozzatura, la repulsione
coulombiana vince l’ azione attrattiva dell’ interazione forte e il nucleo si spezza dando
luogo a due nuclei di massa circa uguale alla metà del nucleo iniziale. Nel processo di
fissione viene liberata una notevole quantità di energia, pari alla differenza di massa del
nucleo padre e della somma delle masse dei frammenti.
Fissione indotta dell’ 235U
INTERAZIONI DELLA RADIAZIONE CON LA MATERIA - 2
In generale il passaggio di particelle cariche nella materia è caratterizzato da due
effetti: la perdita di energia della particella e la deflessione della particella rispetto alla
direzione di incidenza. Questi effetti sono legati alla natura dei processi che avvengono: gli
urti anelastici con gli elettroni atomici del materiale, gli urti elastici con i nuclei.
Queste reazioni avvengono moltissime volte nell’ unità di percorso e il risultato
cumulativo provoca gli effetti osservati. Sebbene siano i processi più probabili, ve ne sono
tuttavia anche altri, in confronto motlo più rari. Ci limitiamo qui a citare il caso della
bremsstrahlung, già vista nel precedente paragrafo, importante meccanismo di perdita di
energia per le particelle cariche leggere. Per ragioni che diventeranno più chiare nel seguito,
separiamo lo studio dei casi di interazione degli elettroni e positroni, da quello di interazione
delle particelle cariche più pesanti (protoni, alfa, etc.), escludendo il caso dei nuclei più
pesanti, che presentano effetti addizionali.
Dei processi fondamentali sopra riportati, gli urti anelastici sono la causa principale
della perdita di energia delle particelle pesanti. In questi urti, l’ energia della particella
incidente si trasferisce all’ atomo, causandone l’ eccitazione (gli elettroni atomici si portano
su stati cui compete un’ energia superiore a quella dello stato fondamentale) o la
ionizzazione (uno o più elettroni acquistano energia sufficiente per abbandonare l’ atomo).
La quantità di energia persa in una collisione singola è in generale una frazione molto
piccola dell’ energia cinetica della particella incidente; tuttavia, nella materia ordinaria
densa, il numero di urti è così elevato da ridurre sostanzialmente l’ energia, anche per
spessori sottili. Per esempio, un protone di energia 10 MeV, perde tutta la sua energia in 0.25
mm di rame.
Gli urti elastici con i nuclei, pur meno frequenti di quelli con gli elettroni atomici,
causano perdite di energia molto piccole, per il fatto che i nuclei di gran parte dei materiali
hanno di solito masse molto maggiori di quelle delle particelle incidenti. Nei casi in cui ciò
non sia vero, per esempio fasci di alfa su bersagli di idrogeno, la perdita di energia in
collisioni nucleari diventa consistente. Anche in questo caso, però, la maggior parte dell’
energia si perde per collisione con gli elettroni atomici.
Gli urti anelastici vanno comunque valutati statisticamente, in quanto la probabilità
che avvengano è determinata dalla meccanica quantistica. Tuttavia, poichè il numero di
interazioni per unità di percorso macroscopico è molto grande, le fluttuazioni della perdita di
energia totale sono piccole, permettendo quindi di valutare la perdita media di energia per
unità di percorso. Questa quantità fu calcolata da Bohr che usò una trattazione classica e
successivamente da Bethe, Bloch e altri che introdussero anche le grandezze quantistiche.
Particelle cariche pesanti, modello classico di Bohr. Consideriamo una particella pesante
di carica Ze, massa M e velocità v, che attraversa un dato materiale. Supponiamo vi sia un
elettrone atomico a distanza b dalla traiettoria della particella. Assumiamo le seguenti
ipotesi:
l’ elettrone sia libero ed inizialmente fermo (il che è ragionevolmente vero se l’ energia della
particella è molto maggiore dell’ energia di legame dell’ elettrone);
durante l’ urto l’ elettrone si sposta pochissimo dalla posizione iniziale, in modo da poter
considerare costante il campo elettrico da esso generato durante tutto il processo;
la particella incidente prosegue dopo l’ urto lungo la traiettoria iniziale, il che è vero se
M>>me.
L’ energia che l’ elettrone acquista nell’ urto si calcola usando il teorema dell’
impulso, per valutare la quantità di moto che esso riceve:
dt
dx
I = ∫ Fdt = e ∫ E perp dt = e ∫ E perp
dx = e ∫ E perp
dx
v
La formula ha il seguente significato:
la forza F che si esercita tra le due particelle è la forza elettrica, quindi F=qE, dove E è il
campo elettrico generato dal’ elettrone. Del campo, per la simmetria del problema, cilindrica,
l’ unica componente che entra nel calcolo è quella perpendicolare alla traiettoria. L’ integrale
∫ E perp dx si calcola usando il teorema di Gauss, applicato ad un cilindro di raggio b
infinitamente lungo il cui asse è la traiettoria della particella incidente. Dunque:
2 Ze
∫ E perp 2 bdx = 4 Ze, ∫ E perp dx = b
l’ impulso è allora:
2 Ze 2
I=
bv
e l’ energia che l’ elettrone acquista:
I2
2Z 2 e 4
∆E (b) =
=
2me me v 2 b 2
Se indichiamo con Ne la densità degli elettroni, l’ energia persa per collisione con tutti gli
elettroni che si trovano a distanza compresa fra b e b+db in uno spessore dx è:
4 Z 2e4
db
− dE (b) = ∆E (b) N e dV =
Ne
dx
2
me v
b
dove dV è l’elemento di volume, dV=2πbdbdx. L’ espressione va integrata per ottenere la
perdita totale di energia. Non è possibile integrare nell’ intervallo di b tra 0 e ∞, perchè
questi estremi non sono compatibili con le ipotesi fatte in partenza. Infatti, per b→∞, cade l’
ipotesi che l’ interazione possa avvenire in un intervallo di tempo piccolo, quindi non si può
utilizzare il teorema dell’ impulso. D’ altra parte, per b→0, si avrebbe un trasferimento
infinito di energia, fisicamente impossibile. Pertanto integreremo in un intervallo compreso
tra bmin e b max, così stimabili: per bmin si cosidera il caso di massimo trasferimento di energia
(caso dell’ urto centrale), per bmax si tiene conto del fatto che l’ elettrone è in realtà legato all’
atomo, attorno al quale si muove con una certa frequenza orbitale. Perchè ci sia realmente
un’ interazione, questa deve avvenire in un tempo breve rispetto alla frequenza orbitale dell’
eletttrone, tipicamente t ≈b/v. Da cui, inserendo il periodo orbitale, si ottiene bmax. Con
queste considerazioni, la perdita di energia è data da:
2
dE 4 Z 2 e 4
mv 3
=
N
ln
e
dx
me v 2
Ze 2
Questo è il risultato classico, valido per particelle pesanti (dall’ alfa in poi). Per i protoni
però la formula non è valida a causa degli effetti quantomeccanici che dominano su quelli
classici. L’ espressione corretta è fornita dalla formula di Bethe-Bloch, la cui trattazione
esula dagli scopi del corso.
Particelle cariche leggere. Anche gli elettroni e i positroni perdono energia per collisioni
quando passano in un materiale. Tuttavia, poichè la loro massa è piccola, oltre ai processi già
esaminati, entra in gioco un ulteriore meccanismo di perdita di energia: l’ emissione di
radiazione elettromagnetica dovuta alla diffusione nel campo elettrico nucleare.
Classicamente, questo fenomeno si spiega con l’ emissione di radiazione dovuta all’
accelerazione di un elettrone (positrone) quando è soggetto alla forza elettrica del nucleo.
Tale radiazione prende il nome di radiazione di frenamento o bremsstrahlung. Il processo di
emissione è funzione dell’ energia dell’ elettrone incidente: fino a pochi MeV è trascurabile,
mentre già ad energie dell’ ordine della decine di MeV la perdita di energia dovuta alla
bremmsstrahlung diventa confrontabile con quella dovuta ai processi di collisione ed
eccitazione. Sopra questo valore, la bremssrahlung domina completamente.
Il ragionamento fatto per le particelle pesanti cariche non può essere ripetuto in
questo caso, essenzialmente per due motivi: il primo, legato alla massa dell’ elettrone,
impedisce di imporre l’ ipotesi che dopo’ urto non ci sia variazione della traiettoria. Il
secondo è che le particelle che urtano sono identiche (elettrone-proiettile ed elettronebersaglio) e quindi il calcolo deve tenere conto dell’ indistinguibilità delle particelle. In più si
deve introdurre anche la perdita di energia per bremsstrahlung. E’ comunque disponibile un’
espressione analoga alla Bethe-Bloch anche per gli elettroni.
−
Effetti biologici. La radiazione è dannosa per i tessuti viventi per il suo potere ionizzante. La
ionizzazione può danneggiare le cellule viventi direttamente rompendo i legami chimici delle
molecole, o indirettamente per formazione di radicali chimici dalle molecole d’ acqua, che
possono attaccare chimicamente le molecole. I più rilevanti sono i danni a carico del DNA.
Entro certi limiti, le cellule sono in grado di riparare i danni molecolari, tuttavia l’ efficacia
dei meccanismi naturali di recupero è funzione dell’ estensione del danno. Se il danno viene
riparato solo in parte o affatto, la cellula è soggetta a tre possibili effetti:
- morte cellulare
- alterazione delle funzioni naturali della cellula che provocano effetti somatici, per
esempio il cancro
- alterazioni permanenti che provocano effetti genetici di trasmissione dei difetti alle
generazioni successive.
Gli effetti di una dose elevata di radiazione in un tempo breve (poche ore) sono a carico dei
processi mitotici di riproduzione. Questo è evidente nei linfociti (globuli bianchi), nei
precursori delle cellule sanguigne nel midollo osseo, nelle cellule di rivestiento dell’
intestino. La diagnosi è dunque possibile tramite un’ analisi del sangue. A dosi
particolarmente elevate può sopravvenire la morte dell’ individuo per infezioni, provocate
dall’ immunodeficienza indotta. La sequenza di eventi è generalmente:
entro i primi due giorni: nausea, vomito, affaticamento, prostrazione
entro le prime sei settimane: alleviamento dei sintomi, recupero dello stato del
paziente oppure
entro le prime otto settimane: emorragie, porpora, letargia, possibile morte
oppure recupero totale.
Se il paziente sopravvive, possono verificarsi effetti a lungo termine del tipo: arrossamneto
della pelle, sterilità, cataratta, aborti o feti malformati.
Ogni effetto, inclusa la morte, ha una soglia caratteristica, ovvero una dose limite al
disotto della quale non si verifica un dato effetto. Questa è essenzialmente legata al numero
di cellule colpite di un dato organo: finchè questo numero è basso, la funzionalità dell’
organo non viene compromessa. Da notare però che organi diversi hanno soglie diverse e che
per uno stesso organo la soglia varia in funzione dell’ età dell’ individuo. Le soglie più basse
si riscontrano negli embrioni (tra l’ ottava e la quindicesima settimana di sviluppo), per i
quali anche dosi molto basse possono provocare alterazioni nello sviluppo. L’ effetto è stato
riscontrato in casi di figli di sopravvissuti ad esplosioni nucleari, che hanno mostrato ritardo
mentale, bassi livelli di QI, etc.
Per dosi basse di radiazione gli effetti possibili sono essenzialmente la possibilità di
sviluppare un tumore o effetti genetici. Per questi non esiste una soglia sicura al disotto della
quale è nulla la probabilità che un effetto si verifichi: Sebbene la statistica in questo caso sia
scarsa, c’è evidenza che il parametro di riferimento sia la dose totale, ovvero quella
accumulata nel tempo. E’ per questo motivo, per esempio, che le Nazioni Unite hanno messo
a punto un programma di prevenzione per i bambini e i ragazzi che vivono nelle aree
adiacenti a Chernobyl (luogo della catastrofe della centrale nucleare ucraina): per alcuni mesi
all’ anno vengono accolti in famiglie che vivono in paesi europei. In tal modo, si allontanano
dalle zone contaminate diminuendo il periodo di esposizione complessivo.