Capitolo 9 – Introduzione alle macchine elettriche
Sezione 9.1: Macchine elettriche rotanti
Problema 9.1
Soluzione:
Quantità note:
Relazione tra potenza nominale e temperatura ambiente mostrata in tabella. Un motore con
funziona a
Trovare :
la potenza reale nelle seguenti condizioni:
a) Temperatura ambiente 50°C
b) Temperatura ambiente 25°C
Ipotesi:
Nessuna.
Analisi:
a) La potenza alla Temperatura ambiente 50°C
b) La potenza alla Temperatura ambiente 20°C
______________________________________________________________________________________
Problema 9.2
Soluzione:
Quantità note:
Caratteristica coppia-velocità di un motore a induzione mostrata in tabella. Il carico richiede una coppia di spunto di 4
Nm e cresce linearmente con la velocità a 8 N·m a 1500 giri/min.
Trovare:
a) Il punto di funzionamento a regime del motore.
b) La variazione in tensione se la coppia di carico aumenta a 10N.
Ipotesi:
Nessuna.
Analisi:
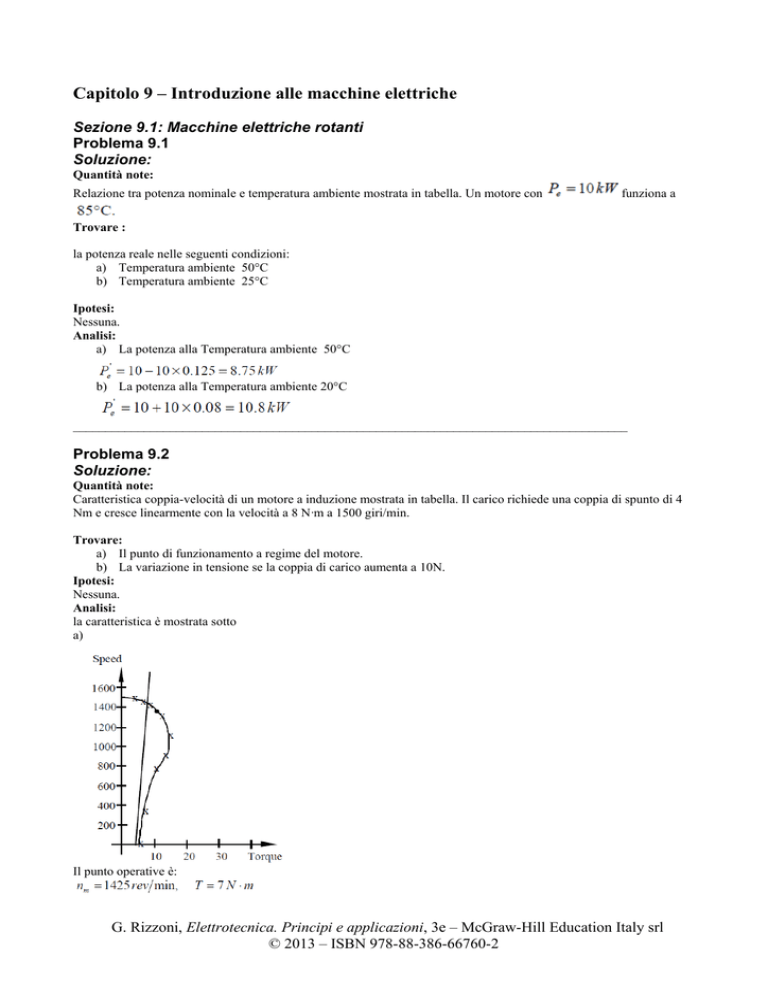
la caratteristica è mostrata sotto
a)
Il punto operative è:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
a) Dalle seguenti equazioni
b)
______________________________________________________________________________________
Paragrafo 9.2: Macchine a corrente continua
Problema 9.3
Soluzione:
Quantità note:
Ciascun conduttore del motore DC è
La corrente è 90 A. La densità di campo è
Trovare:
La forza esercitata da ciascun conduttore di armatura.
Ipotesi:
Nessuna.
Analisi:
______________________
Problema 9.4
Soluzione:
Quantità note:
La densità di flusso nel traferro della macchina DC è
. La superficie della faccia dei poli
.
Trovare:
Il flusso per polo nella macchina
Ipotesi:
Nessuna.
Analisi:
Con
possiamo calcolare il flusso
_________________________________
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Paragrafo 9.3: Generatori
Problema 9.5
Soluzione:
Quantità note:
. La resistenza d’armatura è
Motore shunt
. La corrente di eccitazione parallela è 2A.
Trovare:
La regolazione di tensione del generatore
Ipotesi:
Nessuna.
Analisi:
V L a pieno carico è
e
Assumendo Eb costante si ottiene
Quindi
_______________
Problema 9.6
Soluzione:
Quantità note:
Generatore ad eccitazione separata
. La resistenza d’armatura è
. La corrente di carico è 100A.
Trovare:
a) La tensione generata quando la tensione terminale è 230 V.
b) La potenza di uscita
Ipotesi:
Nessuna.
Analisi:
Se si assume la tensione di uscita nominale, di 230V, si ha
a) Tensione generata 230V.
b) Potenza di uscita 23kW
Se si assume nominale la potenza di uscita,
, si ha
a) Tensione generata 200V.
b) Potenza di uscita 20kW
Se si assume
e si calcola la tensione di uscita come
Abbiamo
a) Tensione generata 210V.
b) Potenza di uscita 21kW
________________________________
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.7
Soluzione:
Quantità note:
Un generatore DC serie
ha resistenza d’armatura
e resistenza di campo
.
Trovare:
a) la corrente di armatura
b) tensione generata
Ipotesi:
Il generatore è alimentato a corrente nominale alla velocità nominale.
Analisi:
il circuito è indicato sotto
____________________________________
Problema 9.8
Soluzione:
Quantità note:
Un generatore con eccitazione parallela
.
ha resistenza d’armatura
e resistenza di campo in serie
Trovare:
a) Potenza sviluppata col carico nominale
b) Correnti di carico, di campo e di armatura
c) Perdite di potenza elettrica
Ipotesi:
nessuna
Analisi:
Il circuito è indicato sotto
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
___________________________________
Problema 9.9
Soluzione:
Quantità note:
Un generatore con eccitazione parallela a 4 poli
ha resistenza d’armatura
e resistenza di campo in
il generatore funziona alla velocità nominale di 3600 giri/min.
serie
Trovare:
Tensione a vuoto del generatore e tensione terminale a metà carico.
Ipotesi:
Nessuna
Analisi:
Per
Usando la relazione
A vuoto
A metà carico
__________________
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.10
Soluzione:
Quantità note:
Un generatore
sta funzionando a metà carico a 1800 giri/min con efficienza dell’85%.
Trovare:
Perdite totali e potenza in ingresso.
Ipotesi:
nessuna
Analisi:
Con un’efficienza dell’85% la potenza di ingresso può essere trovata come:
La perdita totale è:
____________________________
Problema 9.11
Soluzione:
Quantità note:
Generatore DC auto-eccitato . a 2000 giri/min eroga 20° ad una linea a 100V. la resistenza di armatura è
. La
caratteristica di magnetizzazione è mostrata in Fig. 9.11. quando il generatore è disconnesso dalla linea, il motore che lo
alimenta accelera fino a
.
Trovare:
Tensione terminale.
Ipotesi:
Nessuna
Analisi:
Dalla figura,
Per
Quindi
A vuoto
Al tensione terminale è
_________________________
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Sezione 9.4: Motori a corrente continua
Problema 9.12
Soluzione:
Quantità note:
Motore shunt
armatura è
. La resistenza d’armatura è
. La resistenza di campo è 2A. A vuoto la corrente di
e la velocità è 1800 giri/min.
Trovare:
a) la velocità del motore quando la corrente di linea è 62°
b) la velocità di regolazione del motore
Ipotesi:
il flusso non varia col carico. Assumi
Analisi:
_________________________________
Problema 9.13
Soluzione:
Quantità note:
Generatore shunt
di armatura 75A .
. La resistenza d’armatura è
. Funziona a carico e velocità nominale, corrente
Trovare:
Quale resistenza dovrebbe essere inserita nel circuito di armatura per ottenere un 20% di riduzione di velocità quando il
motore sta erogando il 70% della coppia nominale.
Ipotesi:
Il flusso non varia.
Analisi:
________________________
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.14
Soluzione:
Quantità note:
. La resistenza d’armatura è
e la resistenza di carico è
Motore shunt
Funziona a carico e velocità nominale di 1200 giri/min. L’efficienza a pieno carico è 90%.
.
Trovare:
a) la corrente di linea del motore
b) Le correnti di armatura e di campo
c) La fcem a velocità nominale
d) La coppia di uscita
Ipotesi:
Nessuna
Analisi:
la potenza di uscita è
A
.
Dall’efficienza di pieno carico
abbiamo
Da
_______________________________________________________
Problema 9.15
Soluzione:
Quantità note:
. La resistenza d’armatura è
Motore con eccitazione serie
velocità è di 500 giri/min quando la corrente vale 36A.
e la resistenza di campo in serie è
Trovare:
Qual è la velocità del motore quando il carico riduce la corrente di linea a 21A.
Ipotesi:
Tensione sulle spazzole di 3 volt e flusso proporzionale alla corrente.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
. La
Analisi:
_____________________
Problema 9.16
Soluzione:
Quantità note:
Motore con eccitazione parallela
. La resistenza d’armatura è
e la corrente di armatura nominale è
Trovare:
a) Tensione generata sull’armatura
b) Potenza erogata
Ipotesi:
Nessuna
Analisi:
__________________
Problema 9.17
Soluzione:
Quantità note:
Motore con eccitazione serie
. La resistenza d’armatura è
corrente vale 112A e il carico è 75 hp.
e la velocità è di 820 giri/min quando la
Trovare:
L’uscita in potenza del motore quando la corrente passa a 84A.
Ipotesi:
Il flusso è ridotto del 15%.
Analisi:
_________________________________________
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
.
Problema 9.18
Soluzione:
Quantità note:
Motore con eccitazione parallela. La resistenza d’armatura è
1100 giri/min quando la corrente è 4A e non c’è carico.
e la resistenza di campo è
. La velocità è
Trovare:
La tensione E e le perdite rotazionali a 1100 giri/min.
Ipotesi:
Le perdite di carico possono essere trascurate.
Analisi:
corrisponde a
Poiché
, abbiamo:
E quindi
La potenza del motore è
Problema 9.19
Soluzione:
Quantità note:
e la resistenza di campo in serie è
Motore con eccitazione parallela. La resistenza d’armatura è
giri/min,
A carico, la corrente è 46A.
. A 1100
Trovare:
a) La velocità,
e
.
, e la tensione ai terminali varia a 115V trovare
b) Se
Ipotesi:
Nessuna
Analisi:
A vuoto
quindi
A pieno carico,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
La fcem
La potenza erogata è
La potenza disponibile all’albero è:
La coppia disponibile all’albero è:
________________________________________________
Problema 9.20
Soluzione:
Quantità note:
Motore con eccitazione parallela a 200V in DC. La resistenza d’armatura è
è
. A 955 giri/min senza carico,
e la resistenza di campo in serie
, la corrente di linea è 5A.
Trovare:
La velocità del motore, l’efficienza del motore, le perdite totali e la coppia di carico quando il motore preleva 40A dalla
rete.
Ipotesi:
Perdite di potenza rotazionali proporzionali al quadrato della velocità dell’albero.
Analisi:
Perdite nel rame:
Potenza in ingresso:
Quindi:
a
Eb senza carico
Quando
con
e
Potenza sviluppata:
Perdite nel rame:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Potenza in ingresso:
e
Infine, l’efficienza è
Problema 9.21
Soluzione:
Quantità note:
Motore con eccitazione parallela da 50 CV e 230 V opera a pieno carico quando la corrente di linea è 181 A a 1350
giri/min. la resistenza di campo è
. Per aumentare la velocità a 1600 giri/min una resistenza di
dal reostato di campo. La corrente di linea aumenta a 190A.
è eliminata
Trovare:
a) la potenza persa nel campo e la sua percentuale di totale potenza di ingresso per la velocità di 1350 giri/min.
b) Le perdite di potenza nel campo e il reostato di campo per la velocità di 1600 giri/min
c) Le perdite percentuali nel campo e nel reostato di campo a 1600 giri/min
Ipotesi:
nessuna
Analisi:
Problema 9.22
Soluzione:
Quantità note:
Motore con eccitazione parallela da 10 CV e 230 V. La resistenza d’armatura è
è
. Velocità nominale 1000 giri/min. Efficienza a pieno carico 86%.
e la resistenza serie di campo
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Trovare:
L’effetto sulla fcem, corrente di armatura e coppia quando il motore opera a carico nominale e il flusso di campo è
ridotto lentamente al 50% del valore nominale. L’effetto sul funzionamento del motore e la sua velocità quando si
raggiungono nuovamente le condizioni stabili.
Ipotesi:
nessuna
Analisi:
fcem diminuirà
corrente di armatura aumenterà
la coppia è indifferente
Il funzionamento di un motore DC in condizioni di campo indebolito è frequentemente realizzato quando il controllo di
velocità è un importante fattore e dove la diminuzione di efficienza e l’uscita di coppia inferiore a quello nominale
sono di secondaria importanza.
Assumendo piccole variazioni a regime per la corrente Ia
Problema 9.23
Soluzione:
Quantità note:
La macchina è la stessa dell’esempio 9.17, il circuito è mostrato in figura 9.23. la resistenza di armatura è
resistenza di campo trascurabile.
e la
,. Nella regione di funzionamento
Trovare:
a) Il numero di spire di avvolgimento di campo necessario per il funzionamento a pieno carico.
b) la coppia di uscita per le seguenti velocità:
c) Diagramma la caratteristica coppia-velocità per le condizioni della parte b.
Ipotesi:
Nessuna.
Analisi:
nell’esempio 9.17,
la fmm F è:
Per un avvolgimento di campo serie
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Trascurando Rs otteniamo:
Da
Usando
Da
E
otteniamo:
dove
otteniamo
c) Il diagramma è mostrato sotto
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.24
Soluzione:
Quantità note:
Modello circuitale di motore DC PM; modello del carico meccanico. Esempio 9.9
Trovare:
Risposta al gradino di tensione del motore.
Ipotesi:
Nessuna.
Analisi:
Applicando LKTed eq. 9.47 al circuito elettrico:
O
Applicando la seconda legge di Newton l’eq. 9.46 all’inerzia del carico:
O
Poiché la coppia del carico è assunta nulla. Per derivare la funzione di trasferimento da tensione a velocità, usiamo il
risultato dell’esempio 9.9 con
La risposta al gradino del sistema può essere calcolata assumendo un ingresso unitario in tensione:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Per
Dove:
Quindi
Espressioni per la frequenza naturale e rapporto di smorzamento del sistema del secondo ordine possono essere derivati
confrontando la funzione di trasferimento del motore tensione-velocità con una standard del secondo ordine:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Da queste espressioni, possiamo vedere che entrambe la frequenza naturale e il rapporto di smorzamento sono affetti da
ciascuno dei parametri del sistema e che non si può predire la natura dello smorzamento senza conoscere i valori
numerici dei parametri.
Problema 9.25
Soluzione:
Quantità note:
Curve coppia-velocità del motore e del carico:
Trovare:
Velocità di equilibrio e loro stabilità
Ipotesi:
Tutti i coefficienti delle funzioni delle curve coppia-velocità sono costanti positive.
Analisi:
La prima considerazione è che la coppia statica del motore
quindi, la prima condizione è b>d.
deve eccedere la coppia statica del carico,
Il passo successivo è determinare la velocità a regime della coppia motore-carico. Se imponiamo la coppia del motore
uguale alla coppia di carico, le velocità angolari risultanti daranno le soluzioni desiderate.
Risultanti nell’equazione quadratica
Con soluzione
Entrambe le soluzioni sono positive e quindi fisicamente accettabili. Il problema della stabilità può essere risolto come
considerando la seguente Figura
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
In figura vediamo che l’intersezione di una linea con una funzione quadratica quando entrambe le soluzioni sono
positive porta a due possibili situazioni: la linea che interseca la parabola quando la variazione di entrambe le curve è
positiva, e la linea che interseca la parabola quando la variazione della coppia rispetto alla velocità è negativa. Il primo
caso porta ad un punto operativo instabile; il secondo ad uno stabile. Possiamo affermare tale condizione
matematicamente richiedendo che valgano le seguenti condizioni di stabilità a regime:
Valutando per il nostro caso
Da cui si ottiene
È chiaro che
vale sempre, perchè il termine sotto radice è una costante positiva. Quindi, questa coppia motorecarico porta sempre a soluzioni stabili. Per verificare questa conclusione da un punto di vista intuitivo, potresti
diagrammare le curve coppia-velocità di motore e carico e verificare che la condizione
(nota che la figura sopra non è una rappresentazione grafica accurata delle due curve).
___________________________
è sempre soddisfatta
Problema 9.26
Soluzione:
Quantità note:
Espressione per la coppia di attrito e avvolgimento,
, forma funzionale della coppia motore, T, o coppia di carico,
.
Trovare:
Diagrammare caratteristica coppia-velocità.
Ipotesi:
Nessuna.
Analisi:
I diagrammi sono in basso
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.27
Soluzione:
Quantità note:
Motore PM DC e parametri quando 1) a regime senza carico, e 2) connesso alla pompa.
Trovare:
a) coefficiente di smorzamento, diagramma del motore, equazioni dinamiche, funzione di trasferimento e
larghezza di banda a 3 db.
b) Diagramma del motore, equazioni dinamiche, funzione di trasferimento e larghezza di banda a 3 db.
Ipotesi:
Analisi:
a) coppia magnetica bilanciata dalla coppia di smorzamento:
b)
Funzione di trasferimento
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.28
Soluzione:
Quantità note:
Motore PM DC usato per azionare una pompa
Trovare:
Equazioni dinamiche del sistema e funzione di trasferimento tra pressione e tensione del motore.
Ipotesi:
Inerzia e smorzamento del motore e della pompa possono essere considerati insieme.
Analisi:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
schema:
Problema 9.29
Soluzione:
Quantità note:
Circuito del motore mostrato in figura P9.29 e parametri di magnetizzazione, parametri di carico. Punto operativo.
Correzione al punto operativo
Correzione al parametro
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Trovare:
a) equazioni differenziali in forma simbolica
b) equazioni linearizzate
Ipotesi:
Le dinamiche del circuito di campo sono trascurabili
Analisi:
a) equazioni differentiali
Applicando la LKT e l’eq. 9.47 al circuito elettrico:
O
Applicando la seconda legge di Newton e l’eq. 9.46 all’inerzia del carico
O
Poiché le dinamiche del circuito di campo sono molto più veloci di quelle del circuito di armatura
Possiamo scrivere
a)
e il sistema di eq. Diventa
linearizzazione
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Dato che il sistema sta funzionando a regime, possiamo linearizzare l’eq. differenziale per le variabili di perturbazione
introno al punto operativo. Individuiamo i termini nonlineari:
Per linearizzare questi termini, usiamo l’espansione in serie di Taylor del primo ordine:
Scriviamo l’equazione differenziale linearizzata:
Questo set di equazioni è ora lineare e I valori numerici possono essere sostituiti per ottenere la risposta numerica,
valida nell’intorno del punto operativo, per assegnati valori di coppia e tensione al sistema.
Problema 9.30
Soluzione:
Quantità note:
Trovare:
Quale sarà la velocità di rotazione della ventola?
Ipotesi:
La ventola funziona a velocità costante
Analisi:
Applicando la LKT per il motore DC PM
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.31
Soluzione:
Quantità note:
Motore DC con eccitazione separata
Trovare:
a) schema del sistema e sue tree eq. differenziali
b) diagramma a blocchi per simulare il sistema
c) implementare il diagramma in Simulink
d) eseguire la simulazione con Controllo di armatura con tensione di campo costante
. Diagramma velocità
angolare e corrente. Eseguire la simulazione con Controllo di campo con tensione di armatura costante
Diagrammare velocità angolare e corrente.
Ipotesi:
nessuna coppia di carico esterno applicata
Analisi:
a) schema
le 3 equazioni dinamiche sono:
b) Diagramma in Simulink
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
.
c)
controllo di armatura
Controllo di campo
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.32
Soluzione:
Quantità note:
Trovare:
Funzione di trasferimento dalla tensione di armature alla velocità angolare e dalla coppia di carico alla velocità
angolare.
Schemi, diagrammi, circuiti e dati.
Vedi equazione 9.16-18 e fig. 9.20
Analisi:
Applicando la LKT e l’eq. 9.47 al circuito elettrico:
O
O
Per ottenere la funzione di trasferimento utilizziamo la trasformata di Laplace alle due equazioni:
Scriviamo le equazioni in alto in forma matriciale, ri-ordiniasmo e risolviamo applicando Cramer:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.33
Soluzione:
Quantità note:
Un motore DC PM è accoppiato ad una pompa con un lungo albero
Trovare:
Equazioni dinamiche del sistema e funzione di trasferimento dalla tensione di ingresso alla velocità di inerzia del carico
Ipotesi:
La conversione dell’energia è ideale
Analisi:
Sapendo:
Tre equazioni dinamiche del sistema:
In forma matriciali
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.34
Soluzione:
Quantità note:
Parametri del circuito di armatura e di campo; costanti di armatura e di magnetizzazione; inerzia del motore e del carico
e coefficienti di smorzamento.
Trovare:
a) schema del sistema per configurazione serie e parallela
b) scrivere le espressioni delle curve coppia-velocità per ciascuna configurazione
c) scrivere le equazioni differenziali per ciascuna configurazione
d) determinare se le equazioni sono lineari o nonlineari e come possono essere linearizzare.
Analisi:
a) diagramma del sistema
b) scrivi espressioni per le curve coppia-velocità
configurazione parallela
Applicando la LKT e la seconda legge di Newton per il sistema a regime:
Per ottenere la curva coppia-velocità del motore (ci sarà anche un’eq. coppia velocità del carico, ma non abbiamo
informazioni sulla natura del carico), scriviamo
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Sostituiamo l’espressione di Ia nell’equazione del circuito elettrico
O
configurazione serie
Applicando la LKT e la seconda legge di Newton per il sistema a regime:
Per ottenere la curva coppia-velocità del motore (ci sarà anche un’eq. coppia velocità del carico, ma non abbiamo
informazioni sulla natura del carico), scriviamo
Che porta ad un’equazione quadratica in
c) scrivere le equazioni differenziali
configurazione parallela
Applicando la LKT e 9.47 al circuito elettrico:
circuito di campo
O
circuito di armatura
Applicando la seconda legge di Newton e l’equazione 9.46 all’inerzia del carico:
O
Nota che abbiamo tre q. differenziali che devono essere risolte simultaneamente. Se le dinamiche del circuito di campo
sono più veloci di quelle del circuito di armatura (costante di tempo
che la corrente di campo vari istantaneamente con la tensione, portando a:
, come spesso accade) si può assumere
configurazione serie
Applicando la LKT e 9.47 al circuito elettrico:
Applicando la seconda legge di Newton e l’equazione 9.46 all’inerzia del carico:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
O
c)
determinare se le equazioni sono nonlineari.
Entrambi i sistemi di eq. sono nonlineari. Nel caso parallelo, abbiamo i termini prodotto in
e
usiamo il sistema semplificato di due equazioni). Nel caso serie, abbiamo un termine quadratico in
(o in
e
se
e un termine
prodotto in e
. In entrambi i casi nessuna semplice assunzione porta ad un set lineare di equazioni; quindi devono
essere impiegati metodi di soluzione nonlineari oppure bisogna linearizzare.
______________________________________________________________________
Problema 9.35
Soluzione:
Quantità note:
Motore DC con connessone parallela mostrato in fig P9.35
Parametri del motore:
costante d’armatura e riluttanza di coppia e
costante del flusso di campo
Trovare:
Equazioni differenziali descriventi le dinamiche elettriche e meccaniche del motore.
Disegnare un diagramma a blocchi del sistema.
Ipotesi:
Nessuna
Analisi:
sub-sistema elettrico
Sub-sistema meccanico
Diagramma a blocchi per simulazione
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.36
Soluzione:
Quantità note:
Motore DC con connessone serie mostrato in fig P9.36
Parametri del motore:
costante d’armatura e riluttanza di coppia e
costante del flusso di campo
Trovare:
Equazioni differenziali descriventi le dinamiche elettriche e meccaniche del motore.
Disegnare un diagramma a blocchi del sistema.
Ipotesi:
Nessuna
Analisi:
Sub-sistema elettrico
Sub-sistema meccanico
Diagramma a blocchi per simulazione
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Sezione 9.6: L’alternatore (Generatore sincrono)
Problema 9.37
Soluzione:
Quantità note:
Alternatore da 550 VA, 20V. in condizioni nominali,il fattore di potenza è 0.85. la resistenza per fase è
assorbe 2A a 12 V. Le perdite per attrito e di avvolgimento sono 25W e le perdite nel nucleo 30W.
.Il campo
Trovare:
Efficienza percentuale in condizioni nominali.
Ipotesi:
Nessuna.
Analisi:
Problema 9.38
Soluzione:
Quantità note:
Alternatore trifase da 550 kVA, 2300V
di potenza di 0.867 in ritardo.
. La macchina opera a carico e tensione nominali con fattore
Trovare:
Tensione generata per fase e angolo di coppia.
Ipotesi:
Nessuna.
Analisi:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.39
Soluzione:
Quantità note:
Come in Figura P 9.39.
Trovare:
Spiega le funzioni Q , D, Z , and SCR .
Ipotesi:
Nessuna.
Analisi:
Q : Il valore di R1 determina la polarizzazione di Q . Quando Q conduce, SCR si attiverà e darà energia al campo
dell’alternatore
D: Questo diodo serve come elemento di libera circolazione, permettendo alla corrente di campo di circolare senza
interferire con la commutazione di SCR.
Z : il diodo Zener fornisce una prefissata tensione di riferimento all’emettitore del transistor Q; cioè, l’individuazione di
quando Q conduce è controllata solamente dal valore di R1.
SCR : agisce come un raddrizzatore a semi-onda, fornendo l’eccitazione di campo per l’alternatore. Senza il campo,
l’alternatore non può generare.
Sezione 9.7:Il motore sincrono
Problema 9.40
Soluzione:
Quantità note:
Macchina sincrona a due poli, trifase, connessa a stella, a poli non salienti. La reattanza sincrona è
le perdite rotazionali trascurabili. Un punto sulla caratteristica a circuito aperto è dato da
e le resistenze e
(tensione di fase)
. La macchina opera come motore, con una tensione terminale di 400V . la corrente
per una corrente di campo di
di armatura è 50 A , con un fattore di potenza di 0.85 in anticipo.
Trovare:
, corrente di campo, coppia sviluppata e angolo di potenza.
Ipotesi:
Nessuna.
Analisi:
Il circuito per fase è mostrato sotto:
Poiché il fattore di potenza è 0.85:
Da
abbiamo
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Quindi
La coppia sviluppata è
è l’angolo da
a
:
Il diagramma di fase è mostrato sotto:
Problema 9.41
Soluzione:
Quantità note:
Un carico industriale di 900kW con fattore di potenza di 0.6 in ritardo è incrementato aggiungendo un motore sincrono
di 450 kW.
Trovare:
A quale fattore di potenza opera il motore e quale ingresso in potenza è necessario se il fattore di potenza è 0.9 in
ritardo.
Ipotesi:
Nessuna.
Analisi:
Problema 9.42
Soluzione:
Quantità note:
Macchina sincrona a due poli, trifase, connessa a stella, a poli non salienti è connesso ad una linea trifase da 400V, 60
Hz. L’impedenza di statore è 0.5 j1.6 (per fase). Il generatore eroga una corrente nominale di 36 A a fattore di
potenza unitario.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Trovare:
L’angolo di potenza per questo carico e il valore di
in tale condizione. Disegnare lo schema del diagramma fasoriale,
mostrando
Ipotesi:
Nessuna.
Analisi:
L’angolo di potenza è 13.03°.
Problema 9.43
Soluzione:
Quantità note:
Macchina sincrona a due poli, trifase, connessa a stella, a poli non salienti è connesso in parallelo ad un carico trifase
collegato a stella. Il circuito equivalente è mostrato in fig. P9.43. La combinazione parallela è connessa ad una linea
trifase da 220V (fase-fase). LA corrente di carico è 25 A a fattore di potenza di 0.866 induttivo.
funziona con
. Il motore
con un angolo di potenza di -30°.
Trovare:
(al motore), l’intero fattore di potenza e la totale potenza prelevata dalla rete.
Ipotesi:
Trascura tutte le perdite.
Analisi:
Tensione fasoriale per fase è:
Quindi:
Per
La corrente di carico è:
e
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Il fattore di potenza è:
Problema 9.44
Soluzione:
Quantità note:
Macchina sincrona a quattro poli, trifase, connessa a stella, a poli non salienti. Reattanza sincrona
una linea trifase
15 A.
(fase-fase), 60 Hz. Il carico richiede una coppia di
. È connessa ad
. La corrente di linea è
Trovare:
L’angolo di potenza ed E per questa condizione. La corrente di linea quando il carico è rimosso. È in ritardo o in
anticipo sulla tensione?
Ipotesi:
Trascura tutte le perdite.
Analisi:
A
possiamo calcolare
L’angolo di potenza è
Se il carico è rimosso l’angolo di potenza è 0° e da
La corrente è in anticipo sulla tensione.
Problema 9.45
Soluzione:
Quantità note:
Motore sincrono trifase, connesso a stella, da 10 hp, 230 V, 60 Hz eroga la massima potenza con un fattore di potenza
di 0.8 in anticipo. La reattanza sincrona è
. Le perdite rotazionali sono di 230W e le perdite di campo 50W.
Trovare:
a) corrente di armatura
b) efficienza del motore
c) angolo di potenza
Ipotesi:
Trascura la resistenza dell’avvolgimento di statore.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Analisi:
Questo è:
a)
b) Efficienza
c) Angolo di potenza = -27.9°.
Problema 9.46
Soluzione:
Quantità note:
Motore sincrono trifase, 230 V, 60 Hz, 30 poli, 2000 hp, fattore di potenza unitario.
per fase.
Trovare:
Massima potenza e coppia.
Ipotesi:
Trascura tutte le perdite.
Analisi:
A pieno carico
Per fattore di potenza unitario
Coppia e potenza massima
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.47
Soluzione:
Quantità note:
Motore sincrono trifase, connesso a stella, 1200 V, assorbe 110 kW quando funziona con un certo carico a 1200
giri/min. la fcem del motore è 2000 V. Reattanza sincrona
per fase.
Trovare:
La corrente di linea e la coppia sviluppata dal motore.
Ipotesi:
Resistenza di avvolgimento trascurabile
Analisi:
Potenza di ingresso per fase:
Potenza sviluppata
Coppia sviluppata
Problema 9.48
Soluzione:
Quantità note:
Motore sincrono trifase, connesso a stella, 600 V, assorbe 24 kW con un fattore di potenza in anticipo di 0.707.
impedenza per fase
.
Trovare:
Tensione indotta e angolo di potenza del motore.
Ipotesi:
Nessuna
Analisi:
Da
Da
abbiamo
abbiamo
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
L’angolo di potenza è:
Potenza sviluppata
Sezione 9.8: Motore a induzione
Problema 9.49
Soluzione:
Quantità note:
Motore a induzione trifase, 440 V (fase-fase), 60 Hz, 74.6 kW, 4 poli. Parametri del circuito equivalente sono:
La potenza di ingresso a vuoto è 3240W con una corrente di 45 A.
Trovare:
Corrente di linea, potenza di ingresso, coppia sviluppata, coppia all’albero ed efficienza con s 0.02 .
Ipotesi:
Nessuna
Analisi:
Potenza totale trasferita al rotore
Potenza sviluppata
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Potenza rotazionale e perdite di coppia
Coppia sull’albero
Efficienza
Problema 9.50
Soluzione:
Quantità note:
Motore a induzione trifase, connesso a stella, 60 Hz, 4 poli è connesso a linea trifase da 400 V (fase-fase). Parametri del
circuito equivalente sono:
Quando la macchina funziona a 1755 giri/min, le perdite rotazionali e di carico disperso sono 800W.
Trovare:
Scorrimento, corrente di ingresso, totale potenza di ingresso, potenza meccanica sviluppata, coppia all’albero ed
efficienza.
Ipotesi:
Nessuna
Analisi:
abbiamo
Da
Quindi
efficienza
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.51
Soluzione:
Quantità note:
Motore a induzione trifase, 60 Hz, 8 poli opera con uno scorrimento di 0.05 con un certo carico.
Trovare:
a) velocità del rotore rispetto allo statore
b) velocità del rotore rispetto al campo magnetico di statore
c) velocità del campo magnetico di rotore rispetto al rotore
d) velocità del campo magnetico di rotore rispetto al campo magnetico di statore
Ipotesi:
Nessuna
Analisi:
Problema 9.52
Soluzione:
Quantità note:
Motore a induzione trifase, 60 Hz, 2 poli, 400 V per fase sviluppa
Perdite rotazionali a questa velocità 800W.
ad una certa velocità.
Trovare:
a)
Scorrimento e coppia di uscita se la potenza totale trasferita al rotore è 40 kW
e fattore di potenza se
b)
Ipotesi:
Perdite per carico disperso trascurabili
Analisi:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Fattore di potenza è in ritardo
Problema 9.53
Soluzione:
Quantità note:
Velocità di targa di un motore a induzione a 25 Hz è 720 giri/min. La velocità a vuoto è 745 giri/min.
Trovare:
a) scorrimento
b) regolazione percentuale
Ipotesi:
Nessuna
Analisi:
Problema 9.54
Soluzione:
Quantità note:
Dati di targa di un motore a induzione a gabbia di scoiattolo a 4 poli sono:
corrente di linea trifase. Il motore eroga
Trovare:
a)
b)
c)
d)
e)
64 A come
a pieno carico.
scorrimento
regolazione percentuale se la velocità a vuoto è 895 giri/min.
fattore di potenza
coppia
efficienza
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Ipotesi:
Nessuna
Analisi:
Problema 9.55
Soluzione:
Quantità note:
Motore a induzione, connesso a stella, 4 poli, 60 Hz è collegato ad una linea trifase da 200V (fase-fase). I parametri del
circuito equivalente sono:
Il motore funziona con uno scorrimento s 0.04 .
Trovare:
Corrente di ingresso, potenza di ingresso, potenza meccanica, coppia all’albero.
Ipotesi:
perdite per carico disperso trascurabili
Analisi:
Problema 9.56
Soluzione:
Quantità note:
a) Motore a induzione trifase, 220 V, 60 Hz ruota a 1140 giri/min
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
b) Motore ad induzione a gabbia di scoiattolo è avviato riducendo la tensione di linea a
corrente allo spunto.
per ridurre la
Trovare:
a) il numero di poli (per minimo scorrimento), lo scorrimento e la frequenza delle correnti di rotore
b) il fattore di cui risultano ridotte la coppia e la corrente all’avvio
Ipotesi:
Nessuna
Analisi:
a)
per minimo scorrimento la velocità di sincronismo,
giri/min, quindi
, dovrebbe essere il più vicino possibile a 1140
b)
se la tensione di linea è ridotta alla metà, la corrente all’avvio è ridotta di un fattore 2. la coppia sviluppata è
proporzionale a
. Quindi, la coppia allo spunto è ridotta di un fattore 4.
Problema 9.57
Soluzione:
Quantità note:
Una macchina a induzione a 6 poli ha una potenza nominale di 50 kW e un’efficienza dell’85%. Se l’alimentazione è di
220V a 60 Hz.
Trovare:
La velocità del motore e la coppia con uno scorrimento di s = 0.04.
Ipotesi:
Nessuna
Analisi:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.58
Soluzione:
Quantità note: 6 poli
Trovare:
a) velocità e scorrimento della macchina a induzione se una coppia di carico di 50 Nm si oppone al motore.
b) la corrente in valore efficace quando la macchina a induzione opera nelle condizioni di carico del punto a.
Ipotesi:
La curva coppia-velocità è lineare nella regione di nostro interesse.
Analisi:
coppia
velocità del motore
scorrimento del motore
b)
Potenza di uscita
Potenza di ingresso
Corrente
Problema 9.59
Soluzione:
Quantità note:
Motore a induzione trifase, 5 hp, 220V, 60 Hz.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Trovare:
a)
resistenza equivalente di statore per fase,
b) resistenza equivalente di rotore per fase,
c)
reattanza equivalente a rotore bloccato per fase,
Ipotesi:
Nessuna
Analisi:
Problema 9.60
Soluzione:
Quantità note:
Equazione della coppia all’avvio:
Trovare:
a) la coppia allo spunto quando è avviato a 220V.
b) la coppia allo spunto quando è avviato a 110V.
Ipotesi:
nessuna
Analisi:
a)
Problema 9.61
Soluzione:
Quantità note:
Motore a induzione trifase, 4 poli, collegato ad una turbina con caratteristica coppia-velocità data da
Per un certo punto operativo, la macchina ha uno scorrimento del 4% ed un’efficienza dell’87%.
Trovare:
Coppia all’albero turbina-motore
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Potenza totale fornita alla turbina
Potenza totale consumata dal motore
Ipotesi:
Motore alimentato a 60 Hz.
Analisi:
Velocità sincrona del motore a induzione, 4 poli, 60 Hz:
Velocità meccanica del rotore al 4% di scorrimento
Coppia di carico all’albero
Totale potenza fornita alla turbina
Totale potenza assorbita dal motore
Problema 9.62
Soluzione:
Quantità note:
Motore a induzione trifase, 4 poli, ruota a 1700 giri/min quando il carico è 100 Nm.il motore ha un’efficienza dell’88%.
Trovare:
a) scorrimento
b) a potenza costante, carico da 10 kW, la velocità di funzionamento della macchina
c) totale potenza consumata dal motore
d) diagramma le curve coppia-velocità di motore e carico sullo stesso grafico. Mostra i risultati numerici.
Ipotesi:
Motore alimentato a 60 Hz.
Analisi:
a) Velocità sincrona del motore a induzione, 4 poli, 60 Hz:
b) Velocità di funzionamento della macchina per un carico a potenza costante di 10 kW
c) Totale potenza consumata dal motore
d) Diagramma le curve coppia-velocità di motore e carico sullo stesso grafico col punto operativo alla prima
intersezione:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 9.63
Soluzione:
Quantità note:
Motore trifase, 6 poli.
Trovare:
velocità del campo rotante quando il motore è connesso a:
a) linea a 60 Hz;
b) linea a 50 Hz.
Ipotesi:
Nessuna
Analisi:
Problema 9.64
Soluzione:
Quantità note:
Motore trifase a induzione, 6 poli, 440 V, 60 Hz. Le impedenze del modello sono:
Trovare:
Corrente di ingresso e fattore di potenza del motore per una velocità di 1200 giri/min.
Ipotesi:
Nessuna
Analisi:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Per
Il fattore di potenza è
in ritardo
Problema 9.65
Soluzione:
Quantità note:
Motore trifase a induzione, 8 poli, 220 V, 60 Hz. Le impedenze del modello sono:
Trovare:
Corrente di ingresso e fattore di potenza del motore per s = 0.02.
Ipotesi:
Nessuna
Analisi:
Per 8 poli,
Usando il circuito equivalente abbiamo
in ritardo
pf =
Problema 9.66
Soluzione:
Quantità note:
Un esempio di targa è dato nell’esempio 9.2
Trovare:
Coppia nominale, voltampere nominali e massima potenza di uscita in continua per il motore
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Ipotesi:
Nessuna
Analisi:
La velocità è:
I volt-ampere nominali sono:
Massima potenza di uscita in continua del motore
Coppia di uscita nominale
Problema 9.67
Soluzione:
Quantità note:
A tensione e frequenza nominali, la macchina a induzione trifase ha una coppia all’avvio del 140% e una coppia
massima del 210% della coppia a pieno carico.
Trovare:
a) scorrimento a pieno carico
b) scorrimento alla massima coppia
c) corrente di rotore all’avvio in percentuale della corrente di rotore a pieno carico.
Ipotesi:
Trascura le perdite rotazionali e la resistenza di statore. Assumi costante la resistenza di rotore.
Analisi:
a)
Si ottengono 3 eq. in 3 incognite:
Risolvendo le equazioni
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2