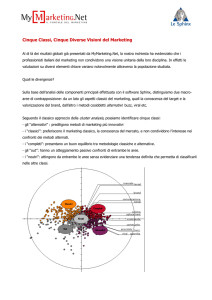
QUADRANTE GEOMETRICO.
(Fonti: W. H. Ryff – Gualterius Rivius, “Der furnembsten, notwendigsten der gantzen Architectur…”,
Norimberga 1547 (1); O. Finé, “La composition et usage du carré géométrique”, Parigi, 1556; J. De
Merliers, “L’usage du carré géométrique”, Parigi, 1568).
Nel corso del XV secolo furono inventati molti nuovi strumenti di misura: ma anche
quelli vecchi vennero studiati e modificati più volte, per adattarli alla risoluzione di
problemi sempre più specialistici, che dovevano essere affrontati con maggiore
rapidità e miglior precisione.
Un caso esemplare è quello del quadrante. Utilizzato nel medioevo solo per misure
astronomiche e topografiche, subì in seguito numerose trasformazioni (la prima,
attribuita a Giorgio di Peuerbach, risale al 1450 circa; fra le successive, citiamo
quella dovuta al matematico e ingegnere italiano Nicolò Tartaglia (2), quasi un secolo
dopo); Oronce Finé indica, nel 1527, ben 57 applicazioni diverse(3) di tale strumento
(fondamentale, tra queste, il rilevamento di membrature architettoniche).
Nella sua forma più semplice, il quadrante geometrico è costituito da un quadrato di
legno col lato di due braccia circa
(1,10 metri): due dei suoi lati sono
suddivisi in sessanta parti ognuno.
Una alidada (o linda) dotata di
mire (traguardi) è incernierata ad
una estremità, nel vertice non
graduato del quadrante stesso.
L’alidada è quindi libera di
spostarsi attorno al punto di cerniera e, mediante le mire, può essere allineata con il
punto da rilevare (4)
La misura della distanza fra due punti, se il terreno è pianeggiante, risulta quasi
immediata. Si voglia, ad esempio, determinare quella tra i punti B’ ed E. Posto uno
dei lati graduati del quadrante (BC nel nostro esempio) in corrispondenza del tratto da
misurare, in modo che uno dei vertici (B nel nostro esempio) coincida con il punto B’
(inizio del tratto da misurare) e tenendo lo strumento verticale, si alza l’asta mobile
(linda, alidada) incernierata in A fino a traguardare il punto E. Si hanno così due
triangoli simili: AFD (con il lato FD graduato) e ABE (con AB lato del quadrante,
BE grandezza incognita). Vale dunque la proporzione AB : DF = BE : AD. Ma il
rapporto AB : DF = k è facilmente calcolabile (servendosi delle graduazioni tracciate
sul lato DC). Risulta pertanto BE = B’E = kAD.
Con lo stesso procedimento è possibile ricavare l’altezza di una torre, la profondità di
una valle, ecc.
Si noti che: il procedimento implica l’ipotesi della propagazione rettilinea del raggio
luminoso (visivo); il punto da rilevare viene traguardato con un solo occhio, quindi
FC è l’immagine prospettica di CE (lunghezza incognita). La geometria necessaria
(del tutto elementare: triangoli simili, teoria delle proporzioni) era studiata (attraverso
esempi e problemi) nelle scuole d’abaco, dove spesso il quadrante (o strumenti
analoghi) venivano utilizzati per esercitazioni.
Utile il confronto tra questo strumento di misura e la “squadra prospettica” descritta
da E. Danti nei commentari alle “Due regole della prospettiva” del Vignola.
(1)
W. H. Ryff, Il manuale necessariamente maneggevole di tutta l’architettura, sottoposta alla servitù degli
occhi, dell’arte matematica e meccanica…., Norimberga 1547, Basilea 1582.
(2)
N. Tartaglia, La nova Scientia, Venezia 1537
(3)
O. Finé, Quadrans astrolabicus omnibus Europae regionibus inserviens, Parigi 1527
(4)
Per questa scheda ci siamo largamente serviti di Docci – Maestri , Storia del rilevamento architettonico e
urbano, Roma, Bari 1993, pag. 115 e segg.