Professoressaaaaaaa:) è andata bene c era un triangolo rettangolo

Professoressaaaaaaa:) è andata bene c era un triangolo rettangolo con il
valore noto della base...bisognava ricavare tramite un'equazione lineare il
valore dell angolo gamma e applicando il teorema dei seni trovare i valori
degli altri lati e calcolare perimetro e area....io sono riuscita a fare
tutto perchè l equazione dava un valore noto della tangente,però sono stata
l unica...nessun altro ci è riuscito e si sono bloccati perchè non sono
riusciti a risolvere l equazione,forse per alcuni radicali....:) grazie
mille e speriamo bene....mi spiace da un lato per gli altri perchè non sono
riuscita a passare nulla,dall altro sono però contenta di aver,incrociando
le dita,dimostrato di aver meritato l otto...buona serata le farò sapere di
tutti appena pubblicano i risultati degli scritti...
triangolo ABC rettandolo in A con lato AB che misura 2 e l angolo gamma col
valore da ricavare dall equazione
radice di 3senx+cosx-2=0 (non trovo la radice nei tasti,il 3 è sotto radice)
Quesito
Dato un triangolo ABC retto in A, con lato AB che misura 2 e l’angolo gamma col
valore da ricavare dall’equazione
radice di 3senx+cosx-2=0
Utilizzando le formula parametriche si ottiene:
2 3t 1  t 2

 2  0 moltiplicando per il m.c.m. abbiamo
t2 1 t2 1
2 3t  1  t 2  2(t 2  1)  0
2 3t  1  t 2  2t 2  2  0
 3t 2  2 3t  1  0 essendo il coefficiente del termine di secondo grado negativo, cambio segno, infine
applicando la formula risolutiva si ottiene:
3t 2  2 3t  1  0 t 
 2 3  43 43 2 3
3


6
6
3
oppure… osservando che il trinomio altro non è che il quadrato di un binomio possiamo scrivere:
( 3t  1) 2  0
3t  1  0
t
1
3

3
3
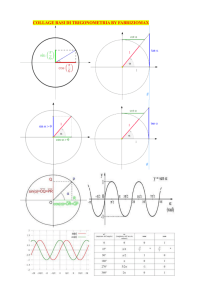
Cambio di variabile e risoluzione dell’equazione elementare in tangente:
tg
x
3
3


; tgy 
; y   k
2
3
3
6
x 
  k
2 6
x2
x


3
6
 2k
 2k
L’equazione lineare presenta infinite soluzioni, dovendo risolvere il problema geometrico, prendiamo in
considerazione la soluzione x=/3, le altre soluzioni sono da scartare in quanto la somma interna degli angoli
di un triangolo rettangolo deve essere uguale a .
Il triangolo è metà di un triangolo equilatero, infatti se il triangolo è rettangolo ed un angolo risulta essere
uguale a 60°, il terzo angolo sarà uguale a 30°.
Le dimensioni dei lati sono legate all’angolo gamma, occorre sapere però se l’angolo gamma è adiacente al
lato AB od opposto!
B
B
A
C
A
C
gamma adiacente ad AB (metà lato del triangolo equilatero):
BC(lato del triangolo equilatero) ipotenusa 4 oppure BC = AB/cos60°=2/(1/2),
AC( altezza del triangolo equilatero)=23 oppure AC/AB=tg60° abbiamo AC=ABtg60°
gamma opposto ad AB (altezza del triangolo equilatero):
BC(lato triangolo equilatero) essendo AB/BC=sen60° quindi
BC=AB/sen60°=2/(3/2)=4/3=43/3
AC (metà lato del triangolo equilatero) AC=23/3 oppure AC/AB=tg30° quindi
AC=ABtg30°=23/3