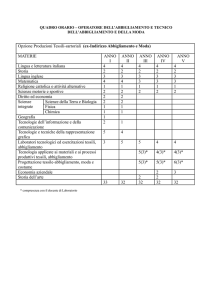
Università Carlo Cattaneo
Corso di laurea in Economia Aziendale (EA-EASI)
STATISTICA I
Prova generale
24 giugno 2003
SOLUZIONI
COMPITO G1
Si riportino ove necessario le formule impiegate per il calcoli
ESERCIZIO 1 (8 punti)
Nel paese A sono presenti 100 negozi che vendono capi di abbigliamento di lusso della marca B. La
probabilità che uno di questi negozi riesca a vendere oggi un capo di abbigliamento dipende inversamente
dal numero di capi di abbigliamento venduti nel giorno precedente: se non ne ha venduti la probabilità è 0.6,
se ne ha venduti da uno a dieci è 0.4, se ne ha venduti più di dieci la probabilità è 0.2. Nella Tabella
sottostante è stata riportata la distribuzione del numero di capi di abbigliamento venduti nell’intera rete di
distribuzione nazionale nella giornata di ieri.
Capi di abbigliamento
0
1-10
più di 10
Negozi
30
45
25
a) Si scriva l’enunciato del teorema delle probabilità totali.
n
Sia data una partizione di , A1,A2,…,An, con Ai tali che i 1 Ai , Ai A j , i j e
P Ai 0
per
i 1, , n .
Sia
B
un
qualsiasi
altro
evento,
allora
PB i 1 P Ai B i 1 P Ai PB | Ai .
n
n
b) Scelto a caso un negozio quale è la probabilità che oggi non riesca a vendere nemmeno un capo di
abbigliamento?
Definito A1 = ”numero di capi di abbigliamento venduti ieri pari a 0”, A2 = ”numero di capi di
abbigliamento venduti ieri da uno a dieci” e A3 = ”numero di capi di abbigliamento venduti ieri più di
dieci” e definito con B l’evento “il negozio ha venduto oggi almeno un capo di abbigliamento”, si ha
che P(A1) = 30/100 = 0.3, P(A2) = 0.45 e P(A3) = 0.25, P(B|A1) = 0.6, P(B|A2) = 0.4 e P(B|A3) = 0.2. Per
il
teorema
delle
probabilità
totali
0.3 0.6 0.45 0.4 0.25 0.2 0.41 e quindi P(Bc) = 0.59.
PB i 1 P Ai PB | Ai
3
c) Si scriva l’enunciato del teorema di Bayes.
n
Sia data una partizione di , A1,A2,…,An, con Ai tali che i 1 Ai , Ai A j , i j e
P Ai 0
i 1, , n . Sia B un qualsiasi
P Ai PB | Ai
P Ai PB | Ai
P Ai | B
.
n
P B
i 1 P Ai PB | Ai
per
altro
evento
con
PB 0 , allora
d) Il negozio C ha venduto oggi un capo di abbigliamento: quale è la probabilità che ieri abbia venduto più
di dieci capi?
Per il teorema di Bayes si ha P A3 | B
P A3 PB | A3 0.25 0.2
0.1220.
P B
0.41
ESERCIZIO 2 (8 punti)
Nel corso dell’anno l’ufficio marketing di una grande società produttrice di capi di abbigliamento di lusso ha
costruito la seguente tabella a doppia entrata dove nelle colonne sono state indicati il numero Xt di capi
venduti nei negozi al tempo t e nelle righe numero Xt-1 di capi venduti nei negozi al tempo t-1. In particolare
sia nelle righe che nelle colonne: “0” indica che nessun capo di abbigliamento è stato venduto, “1-10” indica
che sono stati venduti da uno a dieci capi, “+10” che ne sono stai venduti più di dieci.
Xt 0
Xt-1
0
1-10
+10
12
30
16
1-10
+10
10
15
4
8
5
0
a) Senza effettuare calcoli si dica se le vendite al tempo t-1 e le vendite al tempo t sono indipendenti.
Le vendite nei due istanti non sono indipendenti perché la cella (Xt-1 = +10, Xt = +10) è pari a zero. Se
le vendite fossero state indipendenti allora anche questa cella avrebbe dovuto avere come valore il
prodotto
del
totale
per
di
riga
e
il
per
colonna
corrispondente,
ovvero
n X t 1 10 n X t 10
100
13 20
2.6 0 .
100
b) Come avrebbe dovuto essere la tabella precedente nel caso di indipendenza?
Nel caso di indipendenza la probabilità congiunta dell’evento deve essere uguale al prodotto delle
marginali p X t 1 , X t p X t 1 p X t , da cui dopo aver calcolato le marginali di riga e di colonna
si ottiene
Xt
0
1-10
+10
Xt-1
0
17.4
8.7
3.9
30
1-10
29
14.5
6.5
50
+10
11.6
5.8
2.6
20
58
29
13
100
c) Si determinino le distribuzioni condizionate di Xt|Xt-1. In base alle distribuzioni condizionate è possibile
dire che le vendite non sono indipendenti nei due istanti t e t-1?
Le
distribuzioni
condizionate
sono
pari
a:
0 1 10 10
e X t | X t 1
X t | X t 1 1 10
0.6 0.30 0.10
0 1 10 10
,
X t | X t 1 0
0.4 0.33 0.27
0 1 10 10
. Poiché le
10
0
0.8 0.2
distribuzioni condizionate non sono uguali al variare di t-1, si deduce che Xt e Xt-1 non sono
indipendenti.
ESERCIZIO 3 (8 punti)
L’ufficio marketing di una grande società produttrice di capi di abbigliamento di lusso ha calcolato la
seguente curva di concentrazione della variabile V, volume delle vendite in migliaia di euro dei suoi negozi,
che assume i valori {100, 175, 240}.
Fi
0
0.5
0.7
0.9
1
Qi
0
0.25
0.50
0.80
1
a) Si scriva la funzione di ripartizione e la mediana della variabile V.
v 0 0 v 100 100 v 175 175 v 240 v 240
.
FreqV v FV v
0.5
0.7
0.9
1
0
essendo per la mediana v med min FreqV v 0.5 si ha che v med 100 .
Inoltre
vR
b) Si disegni la curva di concentrazione indicando nel grafico le coordinate dei punti.
1
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
c) Si scriva il valore di un indice di concentrazione per la variabile in esame e, sulla base del suo valore, si
dica se la variabile è poco, molto o mediamente concentrata.
R
F i 1 Qi
i 1 i
3
Calcolando
R
l’indice
di
concentrazione
come
2.1 1.55
0.2619 . La variabile appare poco concentrata.
2.1
3
i1 Fi
3
si
ha
che
d) Sapendo che N = 100 si disegni il grafico della curva di concentrazione nel caso di massima
concentrazione indicando nel grafico le coordinate dei punti.
0
Nel caso di massima concentrazione si ha che V N 1
N
pertanto
Fi N 1
N
Qi 0
N
1 . Le coordinate della curva sono
N
1 N 1
N
N e quindi
1
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.2
0.4
0.6
0.8
1