8829 - METODOLOGIA DELLA RICERCA SOCIALE
Prof. Piergiorgio Corbetta
Conoscenze e abilità da conseguire
Allo studente verranno presentate le principali tecniche di ricerca sociale;
nella parte conclusiva del corso si dedicherà un certo spazio anche
all’analisi dei dati. La finalità del corso è quella di fornire le conoscenze
specifiche necessarie per a) effettuare una ricerca empirica elementare e b)
saper valutare criticamente un rapporto di ricerca.
Programma/Contenuti
Argomenti del corso:
1 - La traduzione empirica della teoria
2 - L'inchiesta campionaria
3 - Le fonti statistiche ufficiali
4 - L'analisi dei dati: analisi ad una variabile
5 - L'analisi dei dati: analisi a due variabili
Testi/Bibliografia
Piergiorgio Corbetta, La ricerca sociale: metodologia e tecniche,
Bologna, Il Mulino
Vol II. Le tecniche quantitative: Cap. I: par. da 1 a 6. Cap. III: par. da 1 a
8. Cap. V: tutto
Vol IV. L'analisi dei dati: Cap. II: par. 1, 2, 3, 8, 12, 13. Cap. III: par. 1,
2 (con esclusione di 2.5, 2.6), par. 7.1 (solo questo sotto-paragrafo del
par. 7)
Alternativamente:
Piergiorgio Corbetta, Metodologia e tecniche della ricerca sociale,
Bologna, Il Mulino
Cap. III: par. da 1 a 6. Cap. V: par. da 1 a 7. Cap. VII: tutto. Cap. XII:
par. 1, 2, 3, 8, 12, 13. Cap. XIII: par. 1, 2 (con esclusione di 2.5 e 2.6),
par. 7.1 (solo questo sotto-paragrafo del par. 7).
Nota: i due programmi sono identici. Si tratta dello stesso volume
pubblicato sia in modo frazionato in quattro volumi (di questi il primo e
il terzo non servono per questo esame) sia in forma di unico volume.
Modalità di verifica dell'apprendimento
Esame scritto: test a risposte multiple.
1
Orario di ricevimento
Mercoledì ore 10-11 presso il Dipartimento di scienze dell'educazione, Via
Filippo Re 6
Calendario Corso
N
Argomento
Lez
1
Introduzione con presentazione ricerche in educazione
2
Ricerca quantitativa e ricerca qualitativa
3
Struttura della ricerca, teoria, ipotesi
4
5
6
L’operativizzazione dei concetti
Le variabili
“
7
8
9
L’inchiesta campionaria
“
“
10
11
12
Le fonti statistiche ufficiali
“
La matrice dei dati
13
14
15
Analisi monovariata
Distribuzioni di frequenza; rappresentazioni tabellari e grafiche
Dati aggregati e rapporti statistici
Serie temporali e territoriali; numeri indice
16
17
18
Analisi bivariata: Tabelle a doppia entrata
“
Esercizi di analisi dati
19
20
21
Analisi bivariata: diagrammi di dispersione
“
Esercizi di analisi dati
2
LUCIDI UTILIZZATI ALLE LEZIONI
Precisazione importante: questi lucidi sono pensati per gli studenti che seguono le lezioni, come
promemoria di quanto fatto a lezione. Non sono assolutamente sufficienti per superare l’esame, né per chi ha
frequentato, né per chi non ha frequentato. Le domande del test d’esame, infatti, fanno riferimento agli
argomenti trattati nel libro adottato, molti dei quali, per la limitatezza del tempo a disposizione delle lezioni,
non sono stati in queste trattati e quindi non compaiono sui lucidi che seguono.
Delle dispense che seguono, le Lezioni n. 1 e n. 2 servono per illustrare i vari tipi di ricerca sociale; gli
esempi ed i temi in esse trattati, tuttavia, non entrano nelle domande del test d’esame.
La numerazione delle lezioni che seguono non corrisponde all’indice delle lezioni sopra riportato: alcuni
degli argomenti delle lezioni che seguono vengono trattati in due lezioni
LEZIONE N 1
ALCUNI ESEMPI DI RICERCHE EMPIRICHE IN CAMPO
EDUCATIVO
Xin Ma, Bullying and Being Bullied: to What Extent Are Bullies also
Victims?, in “American Educational Research Journal”, 2001, pp. 351-370.
Introduzione (rassegna della letteratura)
- Bullismo: una forma di aggressione attraverso la quale uno studente o un
gruppo di studenti ripetutamente disturba una vittima verbalmente o
fisicamente senza essere provocato (es. p. 452)
- Effetti devastanti del bullismo, che spesso arrivando a conseguenza
violante e disastrose sia per le vittime che per gli aggressori
Caratteristiche salienti degli aggressori:
- famiglie con genitori autoritari, ostili, che rifiutano i figli
- precedenti di comportamenti aggressivi
- non c’è relazione con caratteristiche socio-economiche
- genere: più maschi che femmine (3/1)
Caratteristiche salienti delle vittime:
- studenti senza amici nella scuola e eccessivamente protetti dai genitori
- non incidono caratteristiche fisiche (sovrappeso, occhiali, razza, o altre
diversità es. nel vestire, nel dialetto...)
- scarse capacità relazionali, capacità di difendersi o di vendicarsi
- bassa autostima, alta ansietà sociale, paura delle valutazioni negative dei
pari
Caratteristiche del contesto (scuola)
La scuola può far molto per ridurre il bullismo, in quanto gli atti relativi si
compiono in genere negli edifici scolastici:
3
- disciplina, intensa supervisione, assistenza psicologica per studenti,
formazione per gli insegnanti
Metodo
Questionario fatto i due scuole del 6° grado (N=6800) e dell’8° grado
(N=6800), indagando attraverso le domande del questionario se gli
studenti fossero mai stati oggetto di prepotenze o se essi avessero mai
compiuto atti di “bullismo” [Questionario p. 358]
C. Goldenberg, R. Gallimore, L. Reese and H. Garnier, Cause or Effect? A
Longitudinal Study of Immigrant Latino Parents’ Aspirations and
Expectations, and Their Children’s School Performance, in “American
Educational Research Journal”, 2001, pp. 547-582
Studio longitudinale, durato sei anni (dal kindergarten al 6° grado) su 81
bambini latino americani dell’area di Los Angeles, e sui loro genitori. Sul
tema della profezia che si autoadempie: se le aspettative di genitori ed
insegnati sul rendimento scolastico di un bambino sono elevate, il suo
rendimento sarà pure elevato. In particolare pare che il basso successo dei
bambini latino-americani nelle scuole americane sia dovuto al basso livello
di aspettative dei loro genitori.
Strumenti
a. Aspirazioni e attese dei genitori
Ogni anno è stata fatta un’intervista in autunno ai genitori. Domande su
loro aspirazioni e previsioni
a1. Aspirazione: Quanto lei vorrebbe che suo/a figlio/a proseguisse negli
studi?
a2. Attesa (previsione): Fino a quanto lei pensa che suo/a figlio/a prosegua
negli studi?
Per entrambe: finire le elementari / le medie / le superiori / frequentare il
college / frequentare l’università / laurearsi.
b. Risultati scolastici
Basati sulla valutazione degli insegnanti su 4 temi: andamento generale dei
voti nell’anno, andamento nella capacità di lettura, interesse-motivazione,
capacità di apprendimento
4
Fra i risultati emerge non solo, come è noto, che le aspettative dei genitori
influenzano il rendimento scolastico dei figli; ma anche l’interessante fatto
che le aspirazioni dei genitori sono a loro volta influenzate dal rendimento
scolastico dei figli
5
K. J. Quirk, T.Z. Keith e J.T.Quirk, Employment During High School and
Student Achievement: Longitudinal Analysis of National Data, in “The
Journal of Educational Research”, Sept-Oct, 2001, 4-10.
Il fatto che lo studente lavori, che effetto ha sul rendimento scolastico
(studenti delle superiori)?
Incertezze della ricerca sul problema. Effetti sia positivi che negativi.
Alcuni ricercatori hanno trovato effetti leggermente positivi se il lavoro
non supera le 15-20 ore settimanali; negativi se le supera. Nessuno studio
longitudinale.
La ricerca
Campione nazionale di 15.552 studenti dal’8° al 12° grado. Studio
longitudinale (intervistati ogni due anni).
Risultato: influenza curvilinea dell’esperienza di lavoro sul rendimento
scolastico: chi ha lavorato fino a 12 ore alla settimana va meglio di chi non
ha lavorato; gli studenti con lavoro oltre le 12 ore alla settimana sono
quelli che vanno peggio a scuola.
Avvertenza dei ricercatori: bisognerebbe differenziare l’analisi a seconda
del lavoro compiuto (lavoro nei campi, in fabbrica, baby sitting...):
6
J. W. Wimer, C.S. Ridenour, K. Thomas e A.W. Place, Higher Order
Teacher Questioning of Boys and Girls in Elementary Mathematics
Classrooms, in “The Journal of Educational Research”, Nov-Dec, 2001,
84-92.
Ricerca sul diverso rendimento in matematica di maschi e femmine (le
Higher Order Questions sono domande fatte agli studenti che non sono
basate sulla memoria di quanto studiato, ma su un ragionamento
applicativo di queste conoscenze). Bambini e bambine mostrano stesso
entusiasmo per la matematica nella scuola elementare (81% bambine e
84% maschi). Nella prima adolescenza le relazione comincia a cambiare
(72% maschi e 61% femmine). Nella high school è di 25% fra i ragazzi e
15% fra le ragazze.
7
L. Alcàzar et. al., Why are teachers absent? probing service delivery in
Peruvian primary schools, in «International Journal of Educational
Research», 45 (2006): 117-136.
1. Introduction
- Importanza in campo educativo della motivazione degli insegnanti.
2. Literature review: what do we know about teacher absence?
- Pochi studi sistematici, men che meno nella nazione studiata (Perù)
3. Study approach and methodology
- Studio finanziato dalla World Bank sull’assenteismo in campo educativo
e sanitario in 6 nazioni: Peru, Bangladesh, Ecuador, India, Indonesia,
Uganda.
- Visite non annunciate in un campione di 100 scuole elementari distribuite
in 7 regioni rappresentative della costa, sierra e giungla. Due visite: una
per rilevare le presenze, una seconda per intervistare gli insegnanti. Oltre
al questionario individuale (agli insegnanti), anche schede per dati sulla
scuola.
4. Absence and incentives: conceptual framework and Peruvian
institutional context
Fattori che intervengono casualmente sul coinvolgimento degli insegnanti
(incentivi): analisi della letteratura:
Institutional context: stabilità del lavoro, benefici contrattuali (ferie,
pensione...)
Modalità di assunzione: concorsi nazionali, clientele locali...
Salare and bonuses
Monitoring and discipline
5.
Descriptive results: what is the extent of absence and who is absent?
% assenza
Bangladesh
16
Ecuador
14
India
25
Indonesia
19
Peru
11
Uganda
27
8
Segue tabella sulle motivazioni dell’assenza addotte dal direttore
6. Why are school teacher absent?
Analisi multivariata
6.1. Caratteristiche della comunità
. povertà (dell’area)
. lontananza (della scuola)
6.2. Caratteristiche demografiche dell’insegnate
. età, genere, stato civile
6.3. Incentivi finanziari
. salario
6.4. Caratteristiche del contratto
6.5. Controllo e disciplina
. controlli dall’alto dalla gerarchia
. controlli dal basso dalle famiglie
. incentivi non economici: . legami comunitari
. condizioni di lavoro (infarastrutture ed
equipaggiamento
. competizione da parte di scuole private
9
D. Filmer, Gender and wealth disparities in schooling: Evidence from 44
countries, in «International Journal of Educational Research», 43 (2005):
351-369.
1. Introduction
Dichiarazione dei diritti dell’uomo delle nazioni unite del 1948: istruzione
primaria fra i diritti umani. Oltre 50 anni dopo l’obiettivo non è ancora
raggiunto.
Ricerca condotta sui dati del Demographic and Health Surveys (DHS) in
oltre 40 nazioni
2. Why would one expect differences in schooling?
Genere
- diverso valore dato dalle famiglie all’istruzione dei maschi o delle
femmine
- effetto se le scuole sono segregate per genere o se il corpo insegnante è
prevalentemente maschile o femminile
- diverso ruolo di M o F nella produzione familiare: es. cura familiare
(sorelle maggiori che devono prendersi cura dei fratelli e sorelle piccoli),
lavoro nei campi, in casa (es tappeti)
Ricchezza-Povertà
Il reddito familiare influenza l’investimento nella scuola.
Genere e reddito
Poco studiato. P. es. in area rurale potrebbe essere più facile trovare lavoro
per i ragazzi non istruiti (lavori nei campi) per cui ai ragazzi non
converrebbe andare a scuola. All’opposto nelle zone dove le ragazze
sostituiscono la madre nella cura domestica, c’è disincentivo ad andare a
scuola per le ragazze.
3.
Data and methodological approach
Base dati per 44 nazioni, solo paesi “in via di sviluppo”, metà della
popolazione mondiale, campioni nazionali di famiglie fra i 2000 e i 87.000
casi!
Istruzione, tre domande:
se sono mai stati a scuola
più alto livello raggiunto
voto finale avuto
Per coloro che avevano fra 6 e 25 anni chiesto anche se stavano
frequentando una scuola
10
Variabili utilizzate:
- frequenza: % di ragazzi fra 6 e 14 anni che frequentano una scuola
- adempimento: % di giovani fra 15 e 19 anni con i 5 anni delle elementari
Ricchezza-povertà: con dati individuali, vantaggio di poter misurare le
differenze entro le nazioni; tuttavia variabile molto difficile da misurare
(non si può fare domanda diretta su reddito). Utilizzati indicatori su
possesso di beni. Esempio (sommati punteggio 0-15):
- 6 beni posseduti (radio, frigo, tv, bicicletta, moto-auto...)
- 3 indicatori su approvvigionamento acqua
- 3 su servizi igienici
- 1 su elettricità
- 1 di persone in stanza
- 1 su materiale del pavimento della casa
Misure delle disuguaglianze nell’istruzione per genere e ricchezza
Disuguaglianze per genere: rapporto fra M/F frequentanti
Disuguaglianze per ricchezza: (% bambini frequentanti nel 50% delle
famiglie più ricche) / (% bambini frequentanti nel 50% delle famiglie più
povere)
4.
The magnitude on gender and wealth inequalities in education
Disuguaglianze per genere: particolarmente alte nell’Africa centrale e
occidentale; poi in Asia meridionale; poi in Nord Africa. In 7 nazioni la
tendenza è opposta, concentrate in America latina (es Brasile...)
Disuguaglianze per reddito: maggiori in Africa centrale e occidentale, Asia
meridionale, Nord Africa (v. tab. 1)
Confronto fra disuguaglianze di genere e di reddito su istruzione (v. fig. 1)
Linea dei 45°: disug di genere e di ricchezza sono eguali
Quasi tutte le nazioni sono sopra questa linea: le diseg. nell’istruzione per
reddito sono maggiori di quelle per genere.
Tre gruppi:
- nazioni lungo l’asse verticale (Nigeria, Tanzania): diseg. dovute al genere
basse, dovute al reddito alte;
- nazioni con entrambe le disug alte (es. Pakistan)
- nazioni con disug entrambe alte, ma assai maggiore quella per reddito
(es. Mali, Marocco)
11
Problemi della ricerca nelle scienze sociali (Robertson, 34):
- Reattività
- Individualità
- Complessità
- Non-manipolabilità
- Appartenenza
12
LEZIONE N 2
METODI QUANTITATIVI E METODI QUALITATIVI
Fasi del dibattito:
anni 1920-30: confronto
1940-60: trionfo quantitativo
fine anni 60: ritorno del dibattito e della valorizzazione del
qualitativo
dalla seconda metà anni 80: forte sviluppo metodi qualitativi
Quantitativo-qualitativo: contrapposizione dalle radici profonde
Presentazione di due "tipi ideali" di ricerca
A. Paradigma neopositivista:
Sociologia nasce in ambito positivistico
- Auguste Comte, Montpellier1789 - Parigi1857; Cours de philosophie
positive, 1835-1842
- Herbert Spencer, Derby 1820 - Brighton 1903; Principi di filosofia
sintetica, 1862 - 1885.
Ingenuo fideismo metodi scienze naturali.
Positivismo: “studiare la realtà utilizzando gli apparati concettuali, i
metodi di osservazione e misurazione, gli strumenti d'analisi matematica, i
procedimenti d’inferenza, delle scienze naturali”.
Crime in the making, di Robert Sampson e John Laub.
Storia della ricerca: ritrovamento materiale originario ricerca longitudinale
1. Ipotesi teoriche:
- necessità di studio longitudinale, non concentrazione solo su
adolescenza:
. studi trasversali (cross-sectional) o sincronici
. studi longitudinali (longitudinal) o diacronici (prospettiva di ciclo di
vita)
- ipotesi 1: tesi della stabilità del comportamento disadattato
(antisocialità che si forma nell'infanzia)
- ipotesi 2: tesi del cambiamento: i bambini antisociali non diventano
necessariamente degli adulti antisociali: teoria del "controllo sociale
informale";
13
Legami informali in: famiglia, scuola, gruppo dei pari, lavoro,
matrimonio
2. Disegno della ricerca
1939: 500 "autori di reato" e 500 ragazzi "normali" fra i 10 e 17 anni
Seguiti sistematicamente fra il 1939 ed il 1948
Interviste successive all'età di 25 e 32 anni (raggiunti quasi 450 per
gruppo)
3. Analisi dei dati e risultati
Variabili dipendenti:
- devianza ufficiale (autori/non-autori di reato)
- devianza non ufficiale: punteggio sulla base di comportamenti anche
di semplice "cattiva condotta" (fumare, bere, scappare di casa,
marinare la scuola, cattiva condotta a scuola...)
Cinque capitoli:
contesto familiare
ruolo della scuola del gruppo dei pari e di fratelli/sorelle
continuità nel tempo
legami sociali adulti e cambiamento
modelli comparativi di crimine e devianza
Cap. 1: Contesto familiare e delinquenza giovanile
a) quadro teorico:
- la probabilità di devianza cresce col peggiorare delle condizioni socioeconomiche di partenza
- variabili di base o strutturali (structural background variables) e
variabili di processo (processual variables), legami informali (v.
schema a due stadi)
14
Variabili strutturali di base
Affollamento abitativo
Disgregazione familiare
Dimensione familiare
Basso status socio-economico
Nascita all'estero
Mobilità residenziale
Occupazione della madre
Devianza paterna
Devianza materna
b)
c)
Variabili processuali
Padre erratico, freddo e minaccioso
Madre erratica, fredda e minacciosa
Mancanza di supervisione materna
Rifiuto, ostilità da parte dei genitori
Rifiuto dei genitori da parte del ragazzo
Reato
misure empiriche
risultati dell'analisi
regressione standard (devianza non-ufficiale) e logistica (devianza
ufficiale)
. esiste relazione fra variabili di base e devianza (1)
. esiste relazione fra variabili processuali e devianza (2)
. se considerate tutte assieme, le relazioni (1) spariscono: "le variabili
strutturali non hanno effetto diretto sul comportamento deviante, ma
mediato dalle variabili processuali": il 73% dell'effetto (1) è mediato
dalle variabili processuali familiari
Tab. 2.1. Influenza delle variabili strutturali e processuali sul comportamento deviante, sulla base di una regressione
logistica (Sampson e Laub 1993).
b
Variabili strutturali
Mobilità residenziale
Dimensione della famiglia
Affollamento familiare
Disgregazione familiare
Occupazione della madre
Status socio-economico della famiglia
Nascita all'estero
Devianza del padre
Devianza della madre
Variabili processuali
Padre erratico/ostile
Madre erratica/ostile
Supervisione materna
Rifiuto dei genitori
Attaccamento ai genitori
rapporto t
0,03
0,15
-0,32
0,36
-0,11
-0,12
0,00
-0,06
0,15
1,19
2,72*
-1,75
1,50
-0,48
-1,68
0,01
-0,44
0,84
0,48
0,45
-1,24
0,65
-0,38
3,47*
3,35*
-8,16*
3,60*
-2,66*
Chi-quadrato di massima verosimiglianza = 491; gl = 14.
* Indica relazione statisticamente significativa al livello dello 0,05 (p < 0,05)
15
d)
ritorno alla teoria ("i processi familiari di controllo...)
4. Conclusioni teoriche
Applicazione di modello simile a ruolo di scuola, gruppo dei pari, fratelli,
lavoro, matrimonio
Arrivano a un "modello teorico dinamico del crimine, la devianza ed il
controllo sociale informale lungo il ciclo di vita"
16
B. Paradigma interpretativo: Islands in the street, di Martin Sanchez
Jankowski
(Sociologia comprendente, sociologia fenomenologica, ermeneutica)
Wilhelm Dilthey (filosofo tedesco: 1833-1911)
Contrapposizione scienze della natura e scienze dello spirito: lo scopo
delle prime è la spiegazione (Erclären) mentre scopo delle seconde è la
comprensione (Verstehen)
Analisi dell’azione come “una scienza interpretativa in cerca di significato,
non una scienza sperimentale in cerca di leggi”.
“Noi spieghiamo la natura, mentre intendiamo la vita psichica” (Dilthey).
Comprensione o Verstehen, .. fenomeni di empatia e simpatia tra
osservatore ed osservato ... sotto i nomi più diversi: intuizione, percezione
dell’altro, stato mentale, ricostruzione immaginativa (Erlebnis = subitanea
intuizione)
Spiegare e comprendere (“Nelle conclusioni del precedente volume...T 50)
1. Disegno della ricerca e raccolta dei dati
Osservazione partecipante: 37 gang, 10 anni. Partecipazione: 1 mese; 10
giorni; 1 settimana
2. Ipotesi teoriche
Non c'è riflessione teorica pre-empirica basata sulla letteratura, nè
elaborazione di ipotesi da validare empiricamente (la teoria dovrà essere
"scoperta" nel corso dell'indagine). Ipotesi iniziali già derivano dalla
ricerca.
-
la gang non nasce da disorganizzazione sociale ma risponde ad
esigenze di organizzazione per accaparrarsi le scarse risorse
(“L’originalità dell’approccio... T 51)
-
Individuo (tipo ideale) dal "carattere individualistico e ribelle"
(defiant inividualistic character)
. senso della competizione che arriva all'aggressione fisica
. sfiducia verso gli altri (individualismo, isolamento sociale, contare
solo su se stessi)
17
. visione darwinistica del mondo: sopravvivono solo i più forti,
istinto di sopravvivenza
-
Gang (tipo ideale):
. sistema sociale quasi-privato (non aperta a tutti)
. quasi-segreto
. struttura di leadership con ruoli definiti dove l'autorità è passata
attraverso meccanismo di legittimazione
. persegue suoi obiettivi senza preoccuparsi che siano legali o meno
. priva di burocrazia
3. Interpretazione materiale empirico
Tre parti:
- l'individuo ed il suo rapporto con la gang
- la gang come organizzazione
- la gang e la comunità
Cap. 1: Gang involvement. Chi entra in una gang e perché
Risposte date dalla letteratura:
- famiglie disgregate dove padre assente e ricerca di identificazione con
figura d'autorità maschile
- gang come sostituto della famiglia
- espulsi dal sistema scolastico impreparati per poter aspirare a lavoro
- giovanissimi che seguono l'esempio dei più grandi
Secondo Jankonwski tutte risposte sbagliate: si entra nella gang per calcolo
di convenienza razionale. Sei motivazioni incontrate:
- Incentivi materiali
- Divertimento
- Rifugio e nascondiglio
- Protezione fisica
- Luogo di resistenza
- Impegno comunitario
Obiettivo conclusivo: non individuazione di nessi causali ma esperienza
vissuta (capire le manifestazioni nella loro individualità)
18
LEZIONE N 3
STRUTTURA DELLA RICERCA, TEORIA, IPOTESI
1.
LA STRUTTURA “TIPO” DELLA RICERCA QUANTITATIVA
La ricerca scientifica è:
a) un processo creativo di scoperta
b) che si sviluppa secondo un itinerario prefissato e secondo procedure
prestabilite
c) che si sono consolidate all’interno della comunità scientifica
a) Contesto della giustificazione e della scoperta (Let 1)
b) Scienza = accumulazione sistematica di conoscenza (Let 2)
c) La scienza è pubblica e non privata (pubblicità e ripetibilità = controllo)
(Let 3)
Lo scienziato non può fare “di testa sua”
19
La struttura “tipo” del processo di ricerca quantitativa
FASI
PROCESSI
Teoria
Deduzione
Ipotesi
Operativizzazione
(disegno della ricerca)
Rilevazione
Organizzazione dei dati
(matrice-dati)
Analisi dati
Interpretazione
Risultati
Induzione
20
2.
DALLA TEORIA ALLE IPOTESI
Operativizzazione = il processo di traduzione di un’affermazione teorica in
operazioni empiriche
Teoria = insieme di proposizioni organicamente connesse, che si pongono
ad un elevato livello di astrazione e generalizzazione rispetto alla realtà
empirica, le quali sono derivate da regolarità empiriche e dalle quali
possono essere derivate delle previsioni empiriche
Esempio da Durkheim: “più elevato è il tasso di individualismo in un
determinato gruppo sociale, maggiore sarà il tasso di suicidi in quel
gruppo”. Connessione causale con i caratteri di:
- astrazione
- generalizzazione
- derivata da regolarità empiriche
- dà luogo a previsioni
La proposizione teorica si articola in ipotesi specifiche
Ipotesi = interconnessioni fra concetti (in genere un nesso causale, ma non
necessariamente), che si colloca su un livello inferiore di astrazione e di
generalità rispetto alla teoria e che permette una traduzione della teoria in
termini empiricamente controllabili
Rispetto a teoria:
- minor astrazione
- provvisorietà (ipoteticità)
“Empiricamente controllabili”: NON “verificabili”. Verificare =
dimostrare vero; opposto di falsificare (dimostrare falso). Non possiamo
“verificare”, ma solo “non falsificare”. Es “tutti i cigni sono bianchi”
Sequenza teoria-ricerca
Teoria ---> ipotesi specifiche
Revisione della teoria a partire dai risultati (es. astensionismo e
pressioni incrociate)
Sequenza con rilevazione che viene prima della teoria (es. Gambetta;
Sampson e Laub)
21
LETTURE LEZIONE N 3
LET 1
«L'atto della scoperta sfugge all'analisi logica; non vi sono regole logiche
in termini delle quali si possa costruire una "macchina scopritrice" che
assolva la funzione creativa del genio» [Reichenbach 1951, trad. it. 1961,
227
LET 2
Cumulatività:
«Se ho visto più lontano è perché stavo sulle spalle di Giganti» [Isaac
Newton]
Scienza = «accumulazione sistematica di conoscenza»
LET 3
Controllo:
«La scienza è pubblica e non privata»
«I concetti e i procedimenti adoperati anche dal più intuitivo dei sociologi,
devono essere standardizzati, e i risultati delle loro intuizioni debbono
poter essere verificati anche da altri» [Merton 1968, trad. it. 1971, vol. 1,
119].
Pubblicità, Controllabilità, Ripetibilità = «l'unica possibile oggettività della
conoscenza sociologica» [Statera 1984, 250]
22
LEZIONE N 4
OPERATIVIZZAZIONE DEI CONCETTI
1.
DAI CONCETTI ALLE VARIABILI
Ipotesi = interconnessione fra concetti (proposizione che implica una
relazione fra due o più concetti)
Definizione di concetto (Let 1)
Operativizzazione della teoria = operativizzazione dei concetti
Fasi:
1. Far diventare i concetti proprietà di oggetti (unità d’analisi) (es.
partecipazione elettorale e marginalità sociale)
2. Stabilire le regole per la traduzione delle proprietà (degli oggetti) in
operazioni empiriche (“definizione operativa”) (Let 2)
3. Applicare queste regole ai concreti casi studiati (“operativizzazione”
vera e propria)
concetto -----------> proprietà ---------------------> variabile
operativizzazione
(classificazione
ordinamento
misurazione
conteggio)
Definizioni:
proprietà (stati)
variabili (modalità)
23
2.
UNITA’ D’ANALISI
Unità d’analisi = l’oggetto sociale al quale afferiscono le proprietà studiate
(Let3)
Possibili unità d’analisi:
- individuo
(Runciman 1962, 1400 intervistati)
- aggregato di individui
(Tocqueville, regioni francesi)
- gruppo-organizzazione-istituzione (ist. scolast., famiglie, gang, governi)
- evento
(Gurr episodi ribellione, elezioni)
- prodotto culturale
(analisi del contenuto)
Unità d’analisi (singolare, astratta) e casi (plurali, concreti)
24
LETTURE LEZIONE N 4
LET 1
Definizione di concetto
Concetto (cum capio = prendere assieme): contenuto semantico (=
significato) dei segni linguistici e delle immagini mentali
«Il termine “concetto” ha un significato generalissimo, e può includere
ogni specie di segno o procedura semantica, quale che sia l’oggetto cui si
riferisce, astratto o concreto, vicino o lontano, universale o individuale,
ecc. Si può avere un concetto del tavolo come del numero 3, dell’uomo
come di Dio. del genere e della specie... di un periodo storico come di una
istituzione storica (il Rinascimento o il Feudalesimo)» [Abbagnano 1971,
146]. E ancora possiamo dire che i concetti possono far riferimento a
costruzioni mentali astratte che è impossibile osservare direttamente, come
il potere o la felicità o la classe sociale, oppure riferirsi ad entità concrete
ed immediatamente osservabili, come il fiore o l’operaio.
LET 2
La definizione operativa:
Criterio di scientificità: «la necessità di definire operativamente le
proprietà che si studiano è un aspetto caratteristico dell'attività scientifica,
al punto da costituire probabilmente la discriminante più sicura fra essa ed
altri generi di attività, ad esempio la speculazione filosofica» [Marradi
1980, 25].
Criterio di oggettività: «solamente dopo che si è stabilita una catena
di operazioni attraverso le quali lo stato di una serie di soggetti sulle
proprietà X, Y e Z viene rilevato, classificato e registrato, abbiamo
compiuto un passo per ridurre l'opinabilità delle nostre affermazioni»
[ibidem]. La definizione operativa dà infatti le direttive affinché la stessa
rilevazione possa essere replicata da altri ricercatori. In questo modo
riduce la soggettività delle affermazioni del ricercatore. Esse non sono più
opinioni, ma affermazioni dotate di un sostegno empirico.
LET 3
Runciman, W.G.
1966 Relative Deprivation and Social Justice, London, Routledge &
Kegan, trad. it. Ineguaglianza e coscienza sociale, Torino, Einaudi, 1972.
25
Raramente gli atteggiamenti delle persone nei confronti delle ineguaglianze sociali
sono rigorosamente correlati coi fatti che caratterizzano la loro posizione. Si potrebbe
pensare che i sentimenti di una persona verso la struttura della società in cui vive
varino con la sua collocazione; quale che sia il sistema di stratificazione, non è forse
ragionevole aspettarsi che chi sta in alto lo approvi e chi sta in basso ne sia
insoddisfatto? Ma le cose non stanno in questo modo. L’insoddisfazione per il
sistema di privilegi e di compensi di una data società non viene mai provata in
proporzione al grado di ineguaglianza cui sono soggetti i suoi diversi membri. Molti
che stanno in basso hanno meno risentimenti verso il sistema di quanto non sembri
giustificato dalla loro effettiva posizione, e molti più vicini al vertice ne hanno di più.
Il contadino reazionario, il radicale benestante, il povero rispettoso, si ritrovano nella
storia di molti luoghi e di molte epoche: in tutti questi casi c’è una discrepanza tra la
posizione di ineguaglianza e la sua accettazione o il suo rifiuto” [p. 9].
Le nozioni collegate di “privazione relativa” e di “gruppi di riferimento” derivano
entrambe da una banale verifica: gli atteggiamenti, le aspirazioni, le lamentele della
gente, dipendono largamente dallo schema di riferimento all’interno del quale sono
concepite. ... Le soddisfazioni di una persona... sono condizionate dalle sue
aspettative... e per renderci conto dei nostri vantaggi confrontiamo la nostra
situazione con chi sta peggio di noi... Da una parte, una persona che è stata indotta ad
aspettarsi, per esempio, una promozione sul lavoro, si sentirà più offesa dal mancato
ottenimento di quella le cui ambizioni non state ugualmente alimentate. Dall’altra,
una persona condotta all’ospedale dopo un piccolo infortunio si compiangerà molto
meno se posta nel letto accanto a quello di chi è uscito permanentemente invalido da
un grave incidente.
La stessa cosa accade al livello delle classi o anche delle nazioni. E’ diventato un
luogo comune, benché possa apparire a prima vista come un paradosso, che la
povertà costante rappresenta la miglior garanzia della conservazione: se la gente non
ha ragione di aspettarsi o di sperare più di quel che può ottenere, sarà meno scontenta
di quel che possiede, o addirittura sarà grata di riuscire a conservarlo. Se però, d’altro
canto, è stata indotta a scorgere come meta possibile la relativa prosperità di qualche
comunità più fortunata con cui può facilmente confrontarsi, rimarrà scontenta della
sua posizione finché non sarà riuscita a migliorarla. E’ questa naturale reazione che
sta alla base della cosiddetta “rivoluzione delle aspettative crescenti” (17-18)
Per cui «l'aperto malcontento è relativamente raro in periodi di costanti privazioni,
mentre tende a crescere... quando si intravede una possibilità di miglioramento... [ed]
è probabile che le rivoluzioni avvengano in periodi di benessere crescente» [ibidem,
31].
26
LEZIONE N 5
LE VARIABILI
1.
DEFINIZIONE DI VARIABILE
Variabile = concetto operativizzato (più esattamente: proprietà
operativizzata di un concetto)
Fig. 3.2 Dai concetti alle variabili
Peso
Kg 0,7
Operativizzazione
Concetto
Proprietà
Variabile
(peso di un libro)
Peso ---------> Peso di un oggetto------> Peso misurato con bilancia
(concetto)
(proprietà)
(variabile)
Un concetto può essere operativizzato in modi diversi
- può essere associato (come proprietà) a differenti unità d’analisi
es. potere:
. individuo
. ruolo (aziendale, politico)
. istituzione (banca, azienda)
- in quanto proprietà può dar luogo a diverse variabili
es. livello culturale:
. titolo di studio
. numero libri letti
. consumi culturali
. test di cultura generale
27
Variabile = che può variare
Costante
Variazione nel tempo (studio longitudinale, diacronico; es. reazione di un
paziente ad un farmaco)
Variazione fra i casi (studio trasversale, sincronico; es. relazione fra fumo
e cancro al polmone )
Tipi di variabili
- Manipolabilità: variabili manipolabili e non manipolabili
- Causa-effetto: variabili indipendenti e dipendenti
Causa
Effetto
Var indipendente
Var dipendente
Stimolo (trattamento)
Risposta (reazione)
- Osservabilità: variabili latenti ed osservate
- Unità d’analisi: variabili individuali e collettive
Collettive: aggregate e globali
Definizione operativa di una variabile (es. postmaterialismo di Inglehart)
2.
VARIABILI NOMINALI, ORDINALI, CARDINALI
Tipi di variabili
Stati della
Procedura di
Tipo di
proprietà
operativizzazione variabile
Discreti non classificazione
ordinabili
Discreti
ordinamento
ordinabili
nominale
Discreti
enumerabili
Continui
cardinale
conteggio
misurazione
ordinale
“
Caratteristiche Operazioni
dei valori
effettuabili
sui valori
mere etichette = ≠
numeri con
caratteristiche
solo ordinali
numeri con
caratteristiche
cardinali
= ≠ ><
= ≠ ><
+–
28
LEZIONE N 6
L’INCHIESTA CAMPIONARIA
1.
L’INCHIESTA CAMPIONARIA NELLA RICERCA SOCIALE
Conoscere la realtà = osservare, domandare, leggere
Inchiesta campionaria: rilevare informazioni
a) interrogando
b) gli stessi individui oggetto della ricerca
c) appartenenti ad un campione rappresentativo
d) mediante una procedura standardizzata di interrogazione
e) allo scopo di individuare e studiare le relazioni esistenti tra le variabili
Sondaggio (d'opinione): indagine puramente esplorativa volta ad accertare
l'esistenza e la consistenza di un fenomeno.
Inchiesta campionaria si differenzia da sondaggio per:
- problematica teorica (non solo esistenza e consistenza dei fenomeni)
- ampiezza temi toccati
- tipo di analisi sui dati (non solo descrittiva ma anche esplicativa)
Standardizzazione:
DOMANDE
- domanda
- risposta ---> matrice-dati
RISPOSTE
Standardizzate
Libere
Standardiz Questionario
Intervista strutturata
zate
(Inchiesta campionaria survey)
Libere
Intervista libera
ricerca quantitativa
ricerca qualitativa
29
Storia survey
Marx e Weber
L'introduzione del campione rappresentativo (anni 30, Neyman)
Sviluppi tecnologici: computer e telefono
2. LA STANDARDIZZAZIONE OVVERO L’INVARIANZA DELLO
STIMOLO
1.
Approccio oggettivista versus approccio costruttivista
Approccio “oggettivista”: la realtà sociale esiste all’esterno dello studioso
e è da questi oggettivamente conoscibile
Approccio “costruttivista”: l’atto stesso del conoscere produce
un’alterazione della realtà, per cui la realtà conoscibile è solo quella
generata dal processo interattivo fra studiante e studiato
Conseguenze: rapporto intervistato-intervistratore
Lettura: T 175-6
2.
Approccio uniformista versus approccio individualista
Approccio uniformista: esistono se non delle leggi, almeno delle
uniformità empiriche, delle regolarità nei fenomeni sociali e umani
Approccio individualista: irriducibilità dell’individuo umano a qualsiasi
forma di generalizzazione e standardizzazione; comprensione solo
attraverso rapporto empatico; ogni azione sociale è un evento unico
Conseguenze: standardizzazione dello strumento di rilevazione
Lettura: T 176-7
3.
L’obiettivo del minimo comun denominatore
L’obiettivo minimo: il ricercatore che ha scelto l’inchiesta campionaria fa
una scelta di campo: privilegia la ricerca di uniformità rispetto
all’inseguimento dell’individualità; ricerca ciò che accomuna gli individui
piuttosto di ciò che li distingue. Sceglie di lavorare in superficie sui grandi
numeri invece che in profondità sui piccoli
30
3.
L’AFFIDABILITA’ DEL COMPORTAMENTO VERBALE
Lettura: T 179-80 (Williams)
1.
Desiderabilità sociale (delle risposte)
La valutazione socialmente condivisa che in una certa cultura è data ad un
certo atteggiamento o comportamento
2.
Mancanza di opinioni
Gli effetti della “pressione a rispondere” (facilitata anche dalla
formulazione della “domanda chiusa”)
3.3. Intensità
La domanda standardizzata rileva l’opinione, ma non la sua intensità o
radicamento
31
4.
SOSTANZA E FORMA DELLE DOMANDE
Costruire questionario
- esperienza ricercatore (surrogabile con consultazione questionari
precedenti)
- conoscenza popolazione
- chiarezza delle ipotesi
1.
Dati sociografici, atteggiamenti e comportamenti
- Domande relative a proprietà sociografiche di base (descrizione delle
caratteristiche sociali)
- Domande relative a atteggiamenti
- Domande relative a comportamenti: inequivoci (esiste una risposta
esatta), osservabili (esternamente controllabili)
(domande fattuali o motivazionali)
2.
Domande aperte e domande chiuse
Domanda aperta:
- libertà di espressione, ma va comunque codificata per matrice dati; precodifica / post-codifica
Limiti:
- vaghezza delle espressioni
- mancanza di omogeneità negli interventi degli intervistatori
- difficoltà in fase di interpretazione e di codifica
Domanda chiusa:
Vantaggi:
- offre a tutti stesso quadro di riferimento
- facilita il ricordo
- stimola l'analisi e la riflessione
32
Limiti:
- lascia fuori tutte le alternative di risposta che il ricercatore non ha
previsto
- le alternative influenzano le persone (pseudo-opinioni)
- le risposte offerte non hanno lo stesso significato per tutti (e mascherano
l'incomprensione grossolana)
Non è praticabile se:
- le alternative di risposta non sono perfettamente conosciute
- argomenti troppo complessi
- intervistati livello culturale basso
- argomenti delicati
Sintesi:
- sui grandi numeri non c'è alternativa alla domanda chiusa e quindi al
questionario standardizzato
Condizioni per la domanda chiusa:
- tutte le possibili alternative devono essere previste (studio esplorativo)
- non è applicabile:
. quando tutte le possibili alternative di risposta non sono note
. quando sono troppo numerose o complesse
. livello culturale troppo basso degli intervistati
. argomenti delicati
33
5.
FORMULAZIONE DELLE DOMANDE
Esempi formulazione: frati, proibire/non permettere, invasione comunista
1. Semplicità di linguaggio
2. Lunghezza delle domande
3. Numero delle alternative di risposta
4. Espressioni in gergo
5. Definizioni ambigue
6. Parole dal forte connotato negativo
7. Domande sintatticamente contorte
8. Domande con risposta non univoca
9. Domande non discriminanti
10. Domande tendenziose
11. Comportamenti presunti
12. Focalizzazione nel tempo
13. Concretezza-astrazione
14. Comportamenti e atteggiamenti
15. Desiderabilità sociale delle risposte
. formulare le domande legandole a fatti concreti
. rendere accettabile anche la risposta meno desiderabile
. considerare normale e diffuso anche il comportamento negativo
. equilibrare la desiderabilità delle risposte
. attribuire all’intervistato il comportamento negativo
. formulare la domanda in terza persona
16. Domande imbarazzanti
17. Mancanza d’opinione e non so (il non so è legittimo e a volte va
incoraggiato)
18. Intensità degli atteggiamenti
19. Acquiescenza (tendenza a dare risposte affermative e response set)
20. Effetto memoria (stabilire limiti temporali; presentare liste, es. vie
seguite per cercare lavoro; se si può evitare di basarsi sul ricordo,
evitarlo, es. uso diari per i consumi; rischio di attribuire al passato
l’atteggiamento corrente, e band wagon effect)
21. Sequenza delle domande
. dinamica del rapporto intervistato-intervistatore (all’inizio domande
rassicuranti, alla fine imbarazzanti)
. interesse e stanchezza
. sequenzialità dell’intervista (domande a imbuto)
. effetto contaminazione
34
Concludendo:
- effetto della formulazione della domanda soprattutto nell'analisi ad una
variabile, minore sulle loro relazioni
- cautela nei confronti fra domande formulate diversamente (es. nel tempo
o fra nazioni)
- sempre riportare l'esatta formulazione della domanda
35
6.
BATTERIE DI DOMANDE
Domande formulate tutte nello stesso modo (stessa domanda, stesse
alternative di risposta, cambia solo l’oggetto). Finalità:
- risparmiare spazio (sul questionario)
- facilitare la comprensione del meccanismo di risposta
- migliorare la validità delle risposte
- facilitare costruzione di indici
Tecnica delle scale (scaling)
Buon esempio di operativizzazione: domanda su prossimità alla droga da
Quetionario Iard 2000
36
7.
MODALITA' DI RILEVAZIONE
1.
Interviste faccia-a-faccia
Centralità dell’intervistatore
L’intervistatore deve inibirsi qualsiasi comportamento che può influenzare
l'intervistato
Intervistatori:
- Caratteristiche
- Aspettative
- Preparazione
- Motivazione
2.
Interviste telefoniche
Vantaggi:
- rapidità
- costi (telefonata sopra i 60 km costo indifferenziato)
- raggiunge anche i lontani
- minori resistenze alla concessione dell’intervista
- facilita preparazione, coordinamento e supervisione intervistatori
- consente di utilizzare il computer in fase di rilevazione (CATI)
Svantaggi:
- intervistato meno coinvolto (manca contatto personale)
- il rapporto si logora prima (20’ invece che 40-60’)
- impossibile usare materiale visivo
- l'intervistatore non può raccogliere dati osservativi (abitazione, ecc.)
- impossibile per chi non ha telefono (ceti sociali inferiori); difficile per
uso segreterie telefoniche (ceti sociali superiori); molti hanno solo
telefonino (giovani)
- anziani e persone con basso titolo di studio sottorappresentati (malgrado
le istruzioni, es. chi compie per primo gli anni)
- la limitatezza del tempo costringe a semplificazione della domanda e
della risposta
Difetti più gravi: primo e ultimo
37
3.
Questionari autocompilati
Vantaggio:
Limiti:
costi
mancanza di controlli sulla compilazione
autoselezione
Per eliminare gli svantaggi:
- rilevazione di gruppo
- rilevazione individuale con restituzione vincolata (es. censimento)
4.
Questionario postale
Vantaggi:
- risparmi altissimi nei costi
- può essere compilato dall'intervistato quando vuole
- maggiore garanzia di anonimato
- assenza di effetto dell'intervistatore
- accessibilità anche a zone lontane
Svantaggi:
- bassa percentuale di risposte
- distorsione del campione dovuta all'autoselezione
- il livello di istruzione della popolazione: deve essere medio-alto
- mancanza di controllo sulla compilazione (può compilarlo un familiare o
la segretaria)
- impossibilità di questionari complessi (es. evitare le domande
condizionate)
- lunghezza del questionario: deve essere ridotta.
Escludere domande aperte
Problema principale: i "ritorni" (50% buono)
Solleciti: invio con lettera; sollecito (anche cartolina); seconda lettera di
sollecito con nuova copia; telefonata.
5.
Interviste computerizzate (elettroniche)
Cati, Capi, Teleinterviste
38
8.
ORGANIZZAZIONE DELLA RILEVAZIONE
- Studio esplorativo
- Pre-test
- Preparazione e la supervisione degli intervistatori
- Contatto iniziale
- Forma grafica del questionario
39
LEZIONE N 7
LE FONTI STATISTICHE UFFICIALI
ESEMPI: le tabelle sul suicidio di Durkheim (Durkheim_Sucidio.doc)
Statistica: da Stato
Scienza che descrive gli stati
All’inizio ricerca sociale solo con questo tipo di dati. Poi dominio survey
(inchiesta campionaria)
Due significati del termine “statistica” (Devoto-Oli):
- scienza che studia con metodi matematici fondati sul calcolo delle
probabilità fenomeni collettivi (statistica come “scienza”)
(scienza del collettivo: analisi quantitativa dei fenomeni collettivi)
- raccolta di dati che si proponga di dare una visione d’insieme a
determinati fatti (statistica come “dato”)
Utilizzeremo la seconda accezione
Classificazione Istat:
statistiche demografiche
sociali
economiche
ambientali
ESEMPI: Esempi Istat.doc
1.
LA PRODUZIONE
Rilevazione diretta
Censimenti: antichissimi. Sumeri (IV-II millennio a.C), Assiri, Babilonesi,
antico Egitto, impero cinese, Grecia e Roma antiche.
Rilevazione indiretta:
Atti amministrativi: statistiche demografiche, giudiziarie, del commercio
con l’estero, sanitarie, previdenziali ed assistenziali, sul risparmio
Oggi nuovi tipi di rilevazioni dirette: indagini campionarie ad hoc
40
Rilevazione esaustiva (o totale)
Rilevazione campionaria (o parziale)
riduzione dei tempi
riduzione dei costi
riduzione del carico organizzativo
possibilità di approfondimento
2.
LE UNITÀ D’ANALISI
Unità di analisi rappresentata dal territorio (aggregati versus individui)
anche se dati raccolti a livello individuale
. unità di rilevamento
. unità d’analisi
Comuni
Province
Regioni
Sezioni di censimento, sezioni elettorali
Aree metropolitane (attorno ai comuni >250.000 ab): Rm, Mi, Na, To, Pa,
Ge, Bo, Fi, Ba, Ct, Ve
5 ripartizioni geografiche: Italia nord-occidentale
nord-orientale
centrale
meridionale
insulare
Analisi:
variazioni territoriali (nello stesso tempo)
variazioni nel tempo (sullo stesso territorio)
3.
CONTENUTO INFORMATIVO
Solo “comportamenti”
Informazioni generali: Annuario statistico italiano
Aree:
- Popolazione
- Sanità, assistenza e previdenza
41
- Giustizia
- Istruzione e cultura
- lavoro
- Consumi, reddito e benessere
- Elezioni
- Indagini multiscopo sulle famiglie
ESEMPI:
Questionario:
Istat_Quest sicurezza.doc
Istat_Quest condiz salute.doc
Multiscopo: www.istat.it / cerca / multiscopo / la vita quotidiana nel 2006
Ricchissimo di informazioni, molto utile
4. CONCLUSIONI SU USO DELLE FONTI STATISTICHE
UFFICIALI
Indispensabilità
1. Per lo studio della struttura della società. Struttura demografica,
fenomeni migratori, voto politico, occupazione e mercato del lavoro,
struttura di classe, mobilità sociale, organizzazione aziendale e delle
imprese (in generale tutti i fenomeni economici), struttura della famiglia
(figli convivenze, anziani), devianza (reati e attività giudiziaria),
Marginalità sociale, assistenza e previdenza
2. Per lo studio delle ripartizioni territoriali del paese. Differenze fra nord
e sud, regioni, aree metropolitane e non: impossibile da farsi si campioni
della popolazione, a meno che siano di enorme dimensioni (e comunque
non si riesce ad andare al di sotto del dato per regione)
3. Per gli studi comparati fra nazioni. Sempre più importanti (vedi Unione
Europea)
4. Per gli studi nel tempo (longitudinali o diacronici). Analisi delle serie
temporali; studio delle società che hanno preceduto quelle attuali
Limiti
42
1. La natura dei dati può non corrispondere alle esigenze del ricercatore.
Dati già esistenti e raccolti con finalità diverse. Il problema degli
indicatori.
2. Limitati a variabili fattuali. Mancano le motivazioni
3. Non adatti per l'analisi dei comportamenti individuali. Il rischio della
"fallacia ecologica"
43
LEZIONE N 8
LA MATRICE DEI DATI
pagine corrispondenti
- sul testo La ricerca sociale: metodologia e tecniche, Bologna, Il Mulino Vol IV. L'analisi dei dati:
Cap. II: par. 1, 2
- oppure sul testo Metodologia e tecniche della ricerca sociale, Bologna, Il Mulino - Cap. XII: par. 1, 2
QUESTIONARIO (estratto)
Fondazione di ricerca Istituto
Carlo Cattaneo
Via Santo Stefano 11 — 40125 Bologna
RENDIMENTO SCOLASTICO, SENSO CIVICO, IDENTITÀ ITALIANA
E IDENTITÀ EUROPEA TRA I GIOVANI ITALIANI
QUESTIONARIO
Scrivi le risposte nell’apposito spazio oppure indica la tua risposta facendo un cerchietto intorno al
numero corrispondente.
Sigla della provincia in cui si svolge la prova
Tipo di scuola:
Istituto tecnico industriale
Istituto tecnico commerciale
Liceo scientifico
Liceo classico
[1]
[2]
[3]
[4]
Sezione
Cognome e nome (o codice sostitutivo)
Mese e anno di nascita
mese
anno
In quale comune risiedeva la tua famiglia quando sei nato?
Indica anche la sigla della provincia.
In quale comune risiedi? Indica anche la sigla della provincia.
44
Sesso
Maschio
Femmina
[1]
[2]
45
I tuoi genitori lavorano attualmente? Indica una risposta sia per tuo padre sia per tua madre.
Padre
Madre
[1]
[2]
[3]
[4]
[5]
[1]
[2]
[3]
[4]
[5]
Sì, lavora
No, è in pensione
No, è deceduto/a
No, è disoccupato/a
No, è casalingo/a
Che lavoro svolgono tuo padre e tua madre? Se sono in pensione o deceduti o disoccupati, indica l’ultimo
lavoro che hanno svolto.
Padre
[01]
[02]
[03]
[04]
Bracciante, salariato agricolo
Lavorante a domicilio
Affittuario coltivatore, mezzadro
Coltivatore diretto (proprietario)
Madre
[01]
[02]
[03]
[04]
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Operaio
Artigiano senza dipendenti (o coadiuvante in az. familiare artigianale)
Artigiano con dipendenti
[05]
[06]
[07]
[05]
[06]
[07]
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Commerciante senza dipendenti
(o coadiuvante in azienda familiare commerciale)
Commerciante con dipendenti
Impiegato
Insegnante, maestro, docente universitario
[08]
[09]
[10]
[11]
[08]
[09]
[10]
[11]
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Dirigente
Libero professionista
Imprenditore (anche agricolo)
Quali sono i titoli di studio conseguiti dai tuoi genitori?
Indica il titolo sia di tuo padre che di tua madre.
[12]
[13]
[14]
[12]
[13]
[14]
Padre
Madre
[1]
[2]
[3]
[4]
[5]
[1]
[2]
[3]
[4]
[5]
Nessun titolo di studio
Licenza elementare
Licenza di scuola media o avviamento professionale
Diploma di scuola secondaria superiore o di scuola professionale
Laurea universitaria
Con quale giudizio hai conseguito
la licenza di scuola media inferiore?
Sufficiente
Buono
Distinto
Ottimo
[1]
[2]
[3]
[4]
Nel corso della tua frequenza della scuola media superiore, quante volte
sei stato bocciato e hai dovuto ripetere un anno di corso?
Se non sei stato mai bocciato, scrivere «0».
Nel corso della tua frequenza della scuola media superiore, quante volte (cioè in
quanti anni diversi) hai dovuto sostenere esami di riparazione a settembre, oppure
hai dovuto seguire corsi di sostegno e recupero, oppure sei stato promosso con
un «debito formativo»? Se nessuna di queste cose ti è mai successa, scrivere «0».
46
26.
Valuta la gravità di ciascuno dei seguenti comportamenti, indicando un punteggio, dove 5
corrisponde alla massima gravità e 1 corrisponde al minimo di gravità: cerchia il punteggio
corrispondente alla risposta scelta.
Nessuna
Massima
gravità
gravità
Cercare di ottenere dallo Stato benefici cui
non si ha diritto (pensioni di invalidità,
assegni familiari, ecc.)
[1]
[2]
[3]
[4]
[5]
Non pagare il biglietto sui mezzi di trasporto
[1]
[2]
[3]
[4]
[5]
Non pagare le tasse (o pagarle meno del dovuto) [1]
[2]
[3]
[4]
[5]
Comperare qualcosa sapendo che
proviene da un furto (fatto da altri)
[1]
[2]
[3]
[4]
[5]
Prendere e guidare un’auto di
sconosciuti per divertimento
[1]
[2]
[3]
[4]
[5]
Tenersi il denaro trovato
[1]
[2]
[3]
[4]
[5]
Dire il falso nel proprio interesse
[1]
[2]
[3]
[4]
[5]
Accettare denaro non dovuto (una bustarella)
nell’adempimento del proprio dovere
[1]
[2]
[3]
[4]
[5]
Non segnalare il danno fatto senza volerlo
a un veicolo in sosta
[1]
[2]
[3]
[4]
[5]
Gettare rifiuti in un luogo pubblico
[1]
[2]
[3]
[4]
[5]
Passare con il rosso a un semaforo
[1]
[2]
[3]
[4]
[5]
Procurarsi illegalmente il testo di un tema
di esame a un concorso pubblico
[1]
[2]
[3]
[4]
[5]
Dare una somma di denaro a un vigile
per non prendere una pesante multa
[1]
[2]
[3]
[4]
[5]
27.
Negli ultimi tre mesi, con quale frequenza hai partecipato attivamente all’attività dei seguenti
tipi di organizzazioni?
Solo
Almeno
Mai
una volta
2 volte
Organizzazione politica
[1]
[2]
[3]
Organizzazione religiosa o parrocchiale
[1]
[2]
[3]
Organizzazione sportiva (di praticanti)
[1]
[2]
[3]
Organizzazione sportiva (di tifosi)
[1]
[2]
[3]
Organizzazione culturale (teatrale, dibattiti, ecc.)
[1]
[2]
[3]
Organizzazione ricreativa, turistica
[1]
[2]
[3]
Organizzazione per la difesa della natura
[1]
[2]
[3]
Organizzazione di impegno sociale e assistenziale
[1]
[2]
[3]
Collettivi, gruppi di base, centri sociali
[1]
[2]
[3]
Organizzazione studentesca
[1]
[2]
[3]
Organizzazione della gioventù (scout, ecc.)
[1]
[2]
[3]
Organizzazione di tutela dei diritti dell’uomo
[1]
[2]
[3]
47
LIBRO-CODICE (estratto)
Etichetta
colonna
IDENT
PROV
TIPOSKL
ANNONASC
SESSO
CONLAVPA
Codici
Sigla provincia
1 Iti
2 Itc
3 Ls
4 Lc
anno e decennio (99= manca o n.r.)
1 maschi
2 femmine
1
2
3
4
5
9
CONLAVMA
OCC_PAD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
99
OCC_MAD
TITPAD
TITMAD
GIUDMED
BOCC
RIPA
TRASF
TIPOTRAS
occupato
pensionato
deceduto
disoccupato
casalingo
Non risponde/mancante/non deve
Come CONLAVPA
Bracciante
Lav. a domicilio
Affittuario
Coltivatore diretto
Operaio
Artigiano senza dipendenti
Artigiano con dipendenti
Commerciante senza dipendenti
Commerciante con dipendenti
Impiegato
Insegnante
Dirigente
Libero professionista
Imprenditore
Non risponde/mancante/non deve
Come OCC_PAD
1
2
3
4
5
9
Nessuno
Elementare
Scuola media o avv. prof.
Scuola media superiore o prof.
Laurea
Non risponde/mancante/non deve
Come TITPAD
1 sufficiente
2 buono
3 distinto
4 ottimo
9 Non risponde/mancante/non deve
Numero bocciature
(9= Non risponde/mancante/non deve)
Numero riparazioni
(9= Non risponde/mancante/non deve)
1
2
9
1
2
3
9
Unica scuola
Trasferito
Non risponde/mancante/non deve
Ha cambiato tipo di scuola
Non ha cambiato tipo
Non trasferito
Non risponde/mancante/non deve
Corrispondenza con le domande del questionario
(Numero identificazione questionario)
Sigla della provincia in cui ha sede la scuola
Tipo di scuola
Anno di nascita
Sesso
I tuoi genitori lavorano attualmente? Indica una risposta sia per tuo padre
sia per tua madre.
Padre
Madre
Che lavoro svolgono tuo padre e tua madre? Se sono in pensione o deceduti
o disoccupati, indica l’ultimo lavoro che hanno svolto.
Padre
Madre
Quali sono i titoli di studio conseguiti dai tuoi genitori?
Padre
Madre
Con quale giudizio hai conseguito la licenza di scuola media inferiore?
Nel corso della tua frequenza della scuola media superiore, quante volte sei
stato bocciato e hai dovuto ripetere un anno di corso?
Nel corso della tua frequenza della scuola media superiore, quante volte
(cioè in quanti anni diversi) hai dovuto sostenere esami di riparazione a
settembre, oppure hai dovuto seguire corsi di sostegno e recupero, oppure
sei stato promosso con un «debito formativo»?
Questa scuola è l’unica scuola media superiore che hai frequentato oppure ti
sei trasferito da un’altra scuola media superiore?
Hai cambiato tipo di scuola (ad esempio, da liceo classico a liceo scientifico,
da istituto tecnico industriale e istituto tecnico commerciale, e così via)
oppure sei rimasto nello stesso tipo di scuola?
48
NOTA: distribuire un estratto da un questionario (IARD 2000), farlo compilare e codificare
49
Forma della matrice dei dati (casi x variabili: CxV)
codifica
(tracciato record e codice)
Informazioni
-----------------------------------> Matrice dei dati
Casi
1
2
3
n
Matrice dei dati
Variabili
X1
X2
X3
X11
X12
X13
X21
X22
X23
X31
X32
X33
...
...
...
...
...
...
Xn1
Xn2
Xn3
...
...
...
...
...
...
Xp
X1p
X2p
X3p
...
...
...
Xnp
50
Glossario
● l’unità d’analisi (o anche semplicemente unità) è l’oggetto sociale studiato; nella
situazione più frequente l’unità d’analisi è costituita dall’individuo (ma può anche essere la
classe scolastica, la famiglia, il comune, la nazione, l’evento, l’articolo di giornale, ecc.);
● localizzando nel tempo e nello spazio l’unità d’analisi si viene a definire la popolazione
di riferimento (o semplicemente popolazione) della ricerca (per esempio, gli elettori italiani
alle elezioni del 1976; gli episodi di protesta politica avvenuti in Italia fra il 1966 ed il
1973);
● i casi sono gli esemplari dell’unità d’analisi inclusi nella ricerca (per esempio i soggetti
intervistati);
● l’insieme dei casi costituisce il campione studiato;
● le caratteristiche delle unità studiate sono dette proprietà; ogni proprietà può assumere
degli stati diversi (per esempio, la proprietà “pratica religiosa” assume gli stati di
praticante, saltuario, non praticante);
● la variabile è la proprietà operativizzata, cioè rilevata sui casi attraverso una certa
procedura detta “definizione operativa”; per esempio possiamo operativizzare la proprietà
“pratica religiosa” attraverso la domanda “Nell’ultimo anno lei è andato in chiesa?”;
● le modalità sono gli stati della variabile e valori i simboli assegnati alle modalità; i valori
in genere, anche se non necessariamente, sono numeri. Per esempio, la variabile “pratica
religiosa” operativizzata nel modo sopra riportato, ha le seguenti modalità: “mai”, “due-tre
volte l’anno”, “una volta al mese”, “due-tre volte al mese”, “una o più volte la settimana”; i
cui rispettivi valori sono: 1, 2, 3, 4, 5. Se la variabile è nominale gli stati della proprietà
vengono anche chiamati “categorie”;
● variabili dicotomiche (dicotomìe) sono le variabili con due modalità; variabili
politomiche quelle a più di due modalità;
● la matrice dei dati contiene le informazioni raccolte durante un'indagine in forma
numerica e organizzate in forma di rettangolo diviso in righe e colonne, dove ciascuna riga
rappresenta un caso (contiene tutti i dati relativi alle proprietà/variabili di quel caso) e
ciascuna colonna rappresenta una delle proprietà/variabili misurate (contiene i dati di tutti
i casi per quella variabile). Solitamente la matrice dati è contenuta in un file.
● l’analisi monovariata consiste nell’analizzare le variabili singolarmente prese, cioè ad
una ad una senza metterle in relazione fra di loro. In altri termini, si individua la colonna
della matrice-dati corrispondente alla variabile e si conta con che frequenza appaiono i
diversi valori contenuti nella colonna.
● l’analisi bivariata è lo studio delle relazioni fra due variabili. In pratica, si individuano
le due colonne corrispondenti alle due variabili da mettere in relazione e si contano tutte le
diverse coppie di valori presenti nella coppia di colonne. I risultati vengono riportati in
tabelle a doppia entrata.
● l’analisi multivariata è lo studio delle relazioni intercorrenti fra più di due variabili.
51
LEZIONE N 9
L’ANALISI MONOVARIATA
pagine corrispondenti
- sul testo La ricerca sociale: metodologia e tecniche, Bologna, Il Mulino Vol IV. L'analisi dei dati:
Cap. II: par. 3, 8
- oppure sul testo Metodologia e tecniche della ricerca sociale, Bologna, Il Mulino - Cap. XII: par. 3, 8
1.
LE DISTRIBUZIONI DI FREQUENZA: RAPPRESENTAZIONI
TABELLARI
Con il termine "Distribuzione di frequenza di una variabile" si intende la
rappresentazione sintetica (in forma tabellare o grafica), consistente nell’associare ad
ogni modalità (o categoria) della variabile il numero di casi che appartengono a
quella modalità.
Una distribuzione di frequenza può contenere uno o più dei seguenti tipi di
frequenze (vedi tab. 1) :
- Frequenze assolute: cioè il numero di casi per ciascuna categoria della variabile.
- Frequenze relative - proporzioni: posto uguale a 1 il totale dei casi del campione,
per ogni categoria viene riportata la proporzione dei casi che appartengono a quella
categoria (rispetto al totale pari a 1)
- Frequenze relative - percentuali: posto uguale a 100 il totale dei casi del
campione, per ogni categoria viene riportata la percentuale dei casi che
appartengono a quella categoria (rispetto al totale pari a 100)
- Frequenze cumulate percentuali: per ogni categoria viene riportata la percentuale
di casi che appartiene a quella categoria e a quelle di grado inferiore. La frequenza
dell'ultima categoria e sempre 100% (questo tipo di frequenze può essere usato
soltanto con variabili ordinali e cardinali, in quanto richiede che le modalità siano
ordinabili).
Tab. 1 Distribuzione di frequenza della variabile «titolo di studio».
Frequenze
Frequenze
relative
assolutea
Proporzioni
Percentuali
Senza titolo
30
0,025
2,5
Licenza elementare
509
0,424
42,4
Licenza media
342
0,285
28,5
Diploma
264
0,220
22,0
Laurea
55
0,046
4,6
Totale
1200
a dette anche valori assoluti (v.a.)
1,000
Frequenze
cumulate
2,5
44,7
73,4
95,4
100,0
100,0
Come si calcolano le percentuali
30 : 1200 = X : 100
X
30 100
2,5
1200
52
Come si presenta una tabella di distribuzione di frequenza?
- Di solito si usano soltanto le frequenze percentuali; non occorrono segni di
percentuali, perché il tipo di numero è chiaramente indicato nel titolo.
- Inserire nella tavola una riga che riporta il totale 100 (indirizza la lettura)
- Inserire il totale dei casi sui quali le percentuali sono state calcolate (“base” delle
percentuali, vedi la riga intestata con (N)); in questo modo ci si può rendere conto
della significatività della percentuale e inoltre è possibile ricalcolare le frequenze
assolute della distribuzione
- Utilizzare un solo decimale (anche usare numeri interi, senza decimali, va bene); se
il decimale è zero, va riportato (si veda sotto 22,0)
- A volte, si possono ritenere interessanti anche le frequenze assolute, in tal caso si
presentano i dati come in tab. 3.
Quadratura: a causa degli arrotondamenti può succedere che la somma delle
percentuali faccia 99,9 oppure 100,1. In questi casi alterare una cifra per far tornare il
100,0: agendo o sul secondo decimale alterando quello più prossimo a 5 (es. 42,34
diventa 42,4), oppure agendo sulla percentuale più elevata (sulla quale questa
forzatura ha un impatto relativo minore)
Tab. 2 Istruzione degli intervistati. Valori percentuali
Titolo di studio
Senza titolo
2,5
Licenza elementare
42,4
Licenza media
28,5
Diploma
22,0
Laurea
4,6
Totale
100,0
(N)
(1200)
Tab. 3 Distribuzioni di frequenza assolute e relative della variabile
«Partito votato alle elezioni per la Camera del 1996, parte proporzionale»
in Lombardia e in Emilia Romagna (variabile nominale)
Valori assoluti
Valori percentuali
(in migliaia)
Lombardia
Emilia R.
Lombardia Emilia R.
Forza Italia
1510
451
23,6
15,1
Alleanza nazionale
575
344
9,0
11,5
Ccd-Cdu
298
144
4,6
4,8
Lega Nord
1636
216
25,5
7,2
Pds
965
1065
15,1
35,7
Lista Dini
267
116
4,2
3,9
Ppi
398
238
6,2
8,0
Verdi
152
75
2,4
2,5
Rifond. com.
437
249
6,8
8,3
Altri
168
90
2,6
3,0
Totale
6406
2988
100,0
100,0
53
Arrotondamenti
16,751
7
16,7
16,75
16,76
16,8
7
7
7
7
54
Variabili cardinali
Le variabili cardinali come l'età mal si prestano ad essere rappresentate in tabella a
causa dell'elevato numero di categorie. Per cui nella distribuzione di frequenza si
raggruppano i dati in categorie
Tab. 2.4 Distribuzione di frequenza di una
variabile cardinale (distribuzione per età
degli operai di uno stabilimento): valori
singoli e raggruppati in classi.
età
v.a.
classi d'età v.a
15
1
16
2
17
3
15-20
32
18
7
19
7
20
12
21
10
22
12
23
12
21-25
72
24
17
25
21
26
...
26-30
96
...
31-35
112
...
36-40
130
41-45
138
46-50
159
51-55
142
56-60
107
61-65
83
Dati mancanti
Tab. 12.6 Distribuzione di frequenza della variabile nominale «Nell'ultimo anno lei è andato in
chiesa? (se sì) Ogni quanto?».
a) tabella di lavoro
No, mai
2-3 volte l'anno
1 volta al mese
2-3 volte al mese
1 v. la settimana
Più v. la settimana
Altra religione
NR
Totale
1
2
3
4
5
6
7
8
9
b) tabella di presentazione dati
v.a.
132
416
167
233
415
35
11
5
86
1500
No, mai
2-3 volte l'anno
1 volta al mese
2-3 volte al mese
1v. la settimana
Più v. la settimana
Altra religione
Non risponde
Totale
(N)
valori mancanti: 5
%
8,8
27,9
11,2
15,6
27,8
2,3
0,7
5,7
100
(1495)
c) tabella di presentazione
dati
%
No, mai
9,4
2-3 volte l'anno
29,5
1 volta al mese
11,8
2-3 volte al mese
16,5
1v. la settimana
29,5
Più v. la settimana
2,5
Altra religione
0,8
Totale
100
(N)
(1409)
valori mancanti: 91
55
2. LE DISTRIBUZIONI DI FREQUENZA:
RAPPRESENTAZIONI GRAFICHE
Diagrammi a barre (voto per la Camera nel 1996; sui dati di tab. 12.5) Lunghezze della barre proporzionali alle frequenze (ortogrammi)
a) diagramma a barre (a colonne)
Lombardia
30
25
20
15
10
5
0
Forza
Italia
All.
naz.
CcdCdu
Lega
Nord
Pds
Lista
Dini
Ppi
Verdi Rifond.
com.
Altri
b) diagramma a barre (a nastri)
Lombardia
Forza Italia
All. naz.
Ccd-Cdu
Lega Nord
Pds
Lista Dini
Ppi
Verdi
Rif ond. com.
Altri
0
5
10
15
20
25
30
56
c) diagramma a barre appaiate
40
35
30
25
Lombardia
Emilia R.
20
15
10
5
0
Forza
Italia
All.
naz.
CcdCdu
Lega
Nord
Pds
Lista
Dini
Ppi
Verdi Rifond.
com.
Altri
d) diagramma a barre contrapposte
Altri
Rifond. com.
Verdi
Ppi
Lista Dini
Lombardia
Emilia R.
Pds
Lega Nord
Ccd-Cdu
All. naz.
Forza Italia
-40
-20
0
20
40
57
Fig. 12.11 Diagrammi di composizione - Aree proporzionali alle frequenze
(areogrammi)
a) diagramma a barra suddivisa
100%
90%
80%
70%
Boghesia
60%
Classi medie urbane
Coltivatori diretti
50%
Salariati agricoli
40%
Operai ind. e terz.
30%
20%
10%
0%
1881
1983
Classi sociali in Italia nel 1891 e 1993 [Sylos Labini 1986,20]
b) diagramma a settori circolari
Lombardia
7%
3%
2%
24%
Forza Italia
6%
All. naz.
Ccd-Cdu
Lega Nord
4%
Pds
Lista Dini
Ppi
9%
15%
Verdi
Rifond. com.
Altri
5%
25%
Voto nel 1996 in Lombardia (sui dati di tab. prec)
58
LEZIONE N 10
DATI AGGREGATI
pagine corrispondenti
- sul testo La ricerca sociale: metodologia e tecniche, Bologna, Il Mulino Vol IV. L'analisi dei dati:
Cap. II: par. 12, 13
- oppure sul testo Metodologia e tecniche della ricerca sociale, Bologna, Il Mulino - Cap. XII: par.
12, 13
1.
Dati individuali e dati aggregati
Dati individuali: unità d’analisi è l’individuo
Dati aggregati: l’unità d’analisi è un aggregato di individui (es. comune,
regione, nazione...)
Problema dei dati aggregati: diversa dimensione dell’aggregato, per cui i
dati vanno relativizzati alla dimensione dell’aggregato
Fra le seguenti regioni, qual è quella che presenta un maggior tasso di
divorziati ? (Istat, censimento 1991; dati in migliaia)
Piemonte
Lombardia
Emilia R.
Campania
Sicilia
Piemonte
Lombardia
Emilia R.
Campania
Sicilia
Celibi e Coniugati
nubili
1604
2215
3559
4424
1424
2049
2679
2597
2214
2404
Separati
legalmente
57
91
42
24
23
% Divorziati
Totale
(N)
1,02
0,82
0,97
0,36
0,38
4303
8857
3908
5630
4966
Divorziati Vedovi
44
73
38
20
19
383
710
355
310
306
59
Quale di queste città ha il maggior indice di vecchiaia?
Bologna
Napoli
Palermo
Roma
Torino
Venezia
0-14
32.764
196.165
139.435
345.119
99.291
28.954
15-29
62.542
247.757
157.531
521.082
177.544
55.456
30-44
82.548
215.473
146.364
608.546
200.495
63.610
45-64
65 e oltre
Totale
108.094
99.188 385.136
236.136 150.343 1.045.874
154.905
89.620 687.855
723.006 447.569 2.645.322
261.489 180.793 919.612
84.658
63.744 296.422
Due possibilità:
- % di anziani su tutti
- rapporto: popolazione sopra i 65 anni / popolazione sotto i 15
% 65 anni e oltre 65 anni e oltre /
sulla
sotto i 15 anni
popolazione
Bologna
Napoli
Palermo
Roma
Torino
Venezia
25,8
14,4
13,0
16,9
19,7
21,5
3,03
0,77
0,64
1,30
1,82
2,20
60
2.
Rapporti statistici
Rapporti di composizione: parte al tutto (* 100 = percentuali). Esempi:
- Proporzione di spesa per affitto = spesa della famiglia per affitto /
spesa totale della famiglia
- Proporzione di maschi = maschi / (maschi + femmine).
Esempio
Distribuzione dei consumi delle famiglie
2007
Generi
Alimentari
Tabacchi
Abbigliamento
Abitazione
Combustibili
Mobili
Igiene
Trasporti
Istruzione
Altre spese
Totale
Valori
assoluti (in
euro/anno)
3922
212
1447
1818
942
1270
245
2298
912
1800
14866
Valori
percentuali
26,4
1,4
9,7
12,2
6,3
8,5
1,6
15,5
6,1
12,1
100,0
Altro esempio: distribuzione degli studenti dell'università di Bologna per
facoltà
Rapporti di coesistenza: rapporto fra due parti, cioè il rapporto fra la
frequenza di una modalità e la frequenza di un’altra. Esempi:
- Rapporto (o quoziente) di mascolinità = maschi / femmine
- Rapporto di matrimoniabilità per sesso = coniugati / non coniugati
- Occupati nell’industria manifatturiera / occupati in agricoltura.
- Indice di vecchiaia = popolazione sopra i 65 anni / popolazione sotto i
15 anni.
Rapporti di derivazione: rapporto fra la misura di un fenomeno e quella di
un altro che può essere considerato un suo presupposto necessario
- Quoziente di natalità = nati / popolazione x 1.000.
Rientrano in questa categoria molti “quozienti demografici” che hanno
61
alla loro base l’ammontare della popolazione (quoziente di nuzialità, di
mortalità, di immigrazione, di abortività, ecc.). Altri esempi di rapporti di
derivazione sono:
- Laureati / iscritti all’università;
- Pensioni / popolazione;
- Operai cassaintegrati / totale operai;
- Suicidi / popolazione;
- Reati / popolazione.
Rapporti medi: sono diffusissimi e si hanno tutte le volte che il fenomeno
posto al numeratore si può associare mediamente ad ogni unità posta al
denominatore. Per esempio:
- rendimento medio per ettaro = tonnellate di grano prodotto / ettari
coltivati;
- densità della popolazione = n. abitanti / superficie del territorio
(interpretabile come numero medio di abitanti per kmq);
- indice di affollamento = n. componenti la famiglia / n. stanze
dell’abitazione (interpretabile come n. medio di persone per stanza);
- n. posti letto in ospedali / popolazione;
- n. ore di sciopero / n. occupati.
Regione
N posti letto
Valle d'Aosta
Piemonte
Lombardia
Veneto
Liguria
621
35339
63975
47889
17789
N abitanti in
migliaia
112
4479
8892
4345
1808
N posti letto x
1000 abitanti
5,6
7,9
7,2
11,0
9,8
Fare attenzione: rapporto = numeratore / denominatore; massima
attenzione quando gli è concessa libertà di scelta per il denominatore (il
problema non si pone per altri tipi di rapporti, come il rapporto di
composizione).
Tab. 12.20 Rapporti medi. Tassi di fatalità per mezzo di trasporto (Gran Bretagna,
1992).
Incidenti mortali per 100.000 passeggeri
Tipo di trasporto
per viaggio
per ora di viaggio per km percorso
Motocicletta
100
300
9,7
62
Aereo
55
Navigazione
25
Bicicletta
12
A piedi
5,1
Auto
4,5
Furgone
2,7
Treno
2,7
Autobus
0,3
Fonte: «The Economist», 11.1.1997
3.
15
12
60
20
15
6,6
4,8
0,1
0,03
0,6
4,3
5,3
0,4
0,2
0,1
0,04
Serie temporali e serie territoriali
Serie temporale (o serie storica) la sequenza dei valori assunti da una
variabile nello stesso aggregato territoriale in tempi diversi
Serie territoriale la sequenza dei valori assunti da una variabile nello
stesso momento in diversi aggregati territoriali
63
Serie temporale
Tab. 12.21 Andamento dei morti per droga (in valore assoluto) in Italia dal 1985 al
1996
Anno
Morti per Incremento N. indice N. indice
droga (v.a.) percentuale
a base
(1985=100) mobile
1985
242
100
1986
292
20,7
121
121
1987
543
86,0
224
186
1988
809
49,0
334
149
1989
974
20,4
402
120
1990
1161
19,2
480
119
1991
1383
19,1
571
119
1992
1217
-12,0
503
88
1993
888
-27,0
367
73
1994
867
-2,4
358
98
1995
1195
37,8
494
138
1996
1551
29,8
641
130
media
927
dev.stand.
393
Fonte: Ministero dell'Interno
Fig. 12.23 Serie temporale: morti per droga in Italia dal 1985 al 1996
1800
1600
1400
1200
1000
800
600
400
200
0
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
1996
64
Serie territoriale
Tab. 12.22 Suicidi (per 1 milione di abitanti) in Italia nel 1974-83 per regione
Regione
Suicidi
135,41
N. indice
(Italia=100)
288
Valle
d'Aosta
Friuli V.G.
Emilia R.
Umbria
Trentino
A.A.
Piemonte
Liguria
Molise
Toscana
Marche
Abruzzo
Fonte: Istat
Suicidi
Basilicata
49,46
N. indice
(Italia=100)
105
97,27
88,95
82,11
80,43
207
189
175
171
Veneto
Sicilia
Sardegna
Lombardia
43,67
38,15
37,77
37,27
93
81
80
79
70,43
69,95
61,70
60,97
57,70
50,31
150
149
131
130
123
107
Puglia
Lazio
Calabria
Campania
28,14
24,75
24,68
21,08
60
53
53
45
Italia
46,94
100
Italia
Campania
Calabria
Lazio
Puglia
Lombardia
Sardegna
Sicilia
Veneto
Basilicata
Abruzzi
Marche
Toscana
Molise
Liguria
Piemonte
Trentino A.A.
Umbria
Emilia R.
Friuli V.G.
Valle d'Aosta
0
20
40
60
80
100
120
140
160
65
Differenza assoluta e differenza relativa
a = numero morti per droga nel 1985 = 242
b = numero morti per droga nel 1986 = 292
Variazione del numero di morti per droga fra 1985 e 1986
Variazione assoluta: b – a = 292 – 242 = +50
Variazione relativa:
(b - a) : a = X : 100
b–a
a
100=
50
242
100= 20, 7
Nel periodo considerato i casi di morte per droga sono cresciuti del
20,7%.
Numeri indice
“Se ponessimo eguale a 100 i morti per droga nel 1985, a quanto essi
ammonterebbero nel 1986?”
242 : 100 = 292 : X
X=
292
100= 120, 7
242
Quindi il numero di morti per droga fra il 1985 ed il 1986 è passato
da 100 a 120,7
66
Secondo esempio
Generi
Alimentari
Tabacchi
Abbigliamento
Abitazione
Combustibili
Mobili
Igiene
Trasporti
Istruzione
Altre spese
Totale
2007
Valori
assoluti (in
euro/anno)
3922
212
1447
1818
942
1270
245
2298
912
1800
14866
2000
Valori
assoluti (in
euro/anno)
3876
241
1334
1491
923
1278
241
2172
894
1746
14196
N indice
2007
(2000=100)
101
88
108
122
102
99
102
106
102
103
105
67
Numeri indici territoriali
Si pone a 100 il tasso nazionale. Se il tasso di suicidi della Valle d’Aosta è
135,41 e quello nazionale di 46,94, se poniamo il secondo = 100 il primo
diventerà:
46,9 : 100 = 135,41 : X
X=
135, 41
100= 288
46,94
68
I numeri indice:
- non sono mai negativi (quando il valore è inferiore a quello di
riferimento assumono valori inferiori a 100)
- non dipendono dall’unità di misura in cui sono espressi (permettono
confronti fra unità di misura diverse)
Esempio andamento nel tempo di medici ed abitanti in Italia (dati fittizi)
a) valori assoluti
anno medici
abitanti
1881
20.000 30.000.000
1911
30.000 35.000.000
1941
50.000 50.000.000
2001
100.000 60.000.000
70.000.000
60.000.000
50.000.000
40.000.000
medici
abitanti
30.000.000
20.000.000
10.000.000
0
1881
1911
1941
2001
69
b) Numeri indice
medici
1881
1911
1941
2001
abitanti
100
150
250
500
100
117
167
200
600
500
400
medici
300
abitanti
200
100
0
1881
1911
1941
2001
Ancora sul fatto che i numeri indice sono dei “numeri puri”, cioè sono
indipendenti dall’unità di misura dei dati
Variazione dei costi nell’edilizia (dati fittizi)
2000 2007 2000
Materiali
Cemento (alla tonnellata)
Calce (alla tonnellata)
Ferro tondini (al metro)
Legname (per metro cubo)
Mattoni (per confezione di 1000)
Manodopera (paga oraria)
Aree al mq)
215
123
54
18
75
15
215
217
118
75
22
80
25
418
100
100
100
100
100
100
100
2007
101
96
139
122
107
167
194
70
Variazioni nella produzione (valori fittizi)
1970
1980
1990
N automob.
235.000
T. di patate
1.556.000
N televisori
425.200
N laureati
55.213
Posti letto osp
7.245
278.000
1.580.214
1.560.000
84.218
8.213
312.000
1.178.214
2.121.415
115.219
8.432
2000 N. indice
2000
(1970=100)
375.000
1.432.212
1.512.271
218.425
8.546
160
92
356
396
118
Esemplificazione: relazione della Commissione didattica della facoltà
71
LEZIONE 11
ANALISI BIVARIATA: TABELLE A DOPPIA ENTRATA
pagine corrispondenti
- sul testo La ricerca sociale: metodologia e tecniche, Bologna, Il Mulino Vol IV. L'analisi dei dati Cap. III: par. 1, 2 (con esclusione di 2.5, 2.6, 2.7)
- oppure sul testo Metodologia e tecniche della ricerca sociale, Bologna, Il Mulino - Cap. XIII: par.
1, 2 (con esclusione di 2.5, 2.6).
Le tecniche di analisi bivariata
Variabile dipendente
nominale
cardinale
Variabile indipendente
nominale
cardinale
Tavole di
contingenza
Analisi della Regressione
varianza
e correlazione
Le variabili ordinali, a seconda dei casi, possono essere trattate come se fossero
nominali oppure cardinali
1. Che cos'è una tabella a doppia entrata (o tavola di contingenza)
Tab. 2.7 Pratica religiosa per età. (Valori assoluti)
18-34
35-54
Oltre 54
Praticanti
223
313
182
Saltuari
266
317
88
Non praticanti
425
504
168
Totale
718
671
1097
Totale
914
1134
438
2486
Domanda: «Mi può dire con quale frequenza si è recato in chiesa nel corso
dell'ultimo anno?».
Risposte: «Una o più volte la settimana» = Praticanti; «2-3 volte al mese» + «1 volta
al mese» = Saltuari; «2-3 volte all'anno» + «Mai» = Non praticanti. (Fonte: Itanes
[1996]).
- Una tabella a doppia entrata (detta anche "tavola di contingenza" o
"incrocio") è una distribuzione di frequenza a due variabili (di ogni
intervistato considera contemporaneamente la posizione su due variabili,
nell'esempio, pratica religiosa ed età).
72
- Le due variabili sono collocate sulle righe e sulle colonne della tabella;
all'incrocio tra una riga e una colonna troviamo una casella o cella della
tabella. Il numero all’interno è la frequenza con la quale si presentano
congiuntamente le corrispondenti modalità di riga e di colonna (es: 223 =
numero di praticanti fra i 18 e i 34 anni)
- La colonna e la riga 'Totale' si chiamano (frequenze) marginali della
tabella. Sono le distribuzioni semplici di frequenze rispettivamente dell'età
e della pratica. Sono distribuzioni semplici perché si riferiscono a tutto il
campione.
2. A cosa serve una tabella a doppia entrata
- Serve a studiare la relazione tra due variabili.
- Si dice che c'è relazione tra due variabili (età e pratica nell'esempio) se
dividendo il campione in sottocampioni secondo una variabile (l'età:
giovani, adulti, anziani) la distribuzione semplice della seconda variabile
(la pratica religiosa) è diversa nei differenti sottocampioni di età.
Viceversa, se le distribuzioni sono identiche si dice che non c'è relazione.
- La variabile usata per dividere il campione in sottocampioni è detta
variabile indipendente, la variabile di cui si studia la distribuzione nei
sottocampioni è detta variabile dipendente.
- Da un punto di vista statistico sia l'età che la pratica religiosa possono
assumere il ruolo di variabile indipendente. Dal punto di vista sociologico,
tuttavia, non ha molto significato chiedersi se la distribuzione delle età
varia al variare della pratica religiosa, come se la pratica di un soggetto
potesse influire sulla sua età.
- Nella tabella 2.7 compaiono frequenze assolute: è difficile dire a colpo
d'occhio se la proporzione di praticanti tra i giovani è maggiore, minore,
uguale a quella dei praticanti tra gli anziani. Per questo è necessario
passare al calcolo percentuale (percentualizzare significa porre uguale a
100 il totale; in tal modo si rendono uguali i totali dei gruppi da
confrontare che così diventano confrontabili)
73
3. Direzione delle percentuali nelle tabelle a doppia entrata
Tab. 2.7 Pratica religiosa per età. (Valori assoluti)
18-34
35-54
Oltre 54
Praticanti
223
313
182
Saltuari
266
317
88
Non praticanti
425
504
168
Totale
914
1134
438
Totale
718
671
1097
2486
Tab. 2.8 Pratica religiosa per età. (Valori percentuali per riga)
18-34
35-54
Oltre 54
Totale
Praticanti
31,1
43,6
25,3
100,0
Saltuari
39,6
47,2
13,1
100,0
Non praticanti
38,7
45,9
15,3
100,0
Tab. 2.9 Pratica religiosa per età. (Valori percentuali per colonna)
18-34
35-54
Oltre 54
Praticanti
24,4
27,6
41,6
Saltuari
29,1
28,0
20,1
Non praticanti
46,5
44,4
38,4
Totale
100,0
100,0
100,0
Tab. 2.10 Pratica religiosa per età. (Valori percentuali sul totale)
18-34
35-54
Oltre 54
Totale
Praticanti
9,0
12,6
7,3
28,9
Saltuari
10,7
12,8
3,5
27,0
Non praticanti
17,1
20,3
6,8
44,1
Totale
36,8
45,6
17,6
100,0
74
1. La percentualizzazione per riga (tab. 2.8) risponde a questa domanda:
il gruppo dei praticanti è mediamente più giovane o più anziano
rispetto ai non praticanti e ai saltuari? Non è una domanda 'esplicativa',
non intendiamo che essere praticante o meno abbia effetti sull'età
dell'intervistato, il nostro scopo è meramente descrittivo.
2. La percentualizzazione per colonna (tab. 2.9) risponde a questa
domanda: "l'età degli intervistati influenza il loro grado di pratica
religiosa?". Come si vede si tratta di una domanda esplicativa: "l'età è
la causa della pratica religiosa?".
3. La percentualizzazione sul totale (tab. 2.10) risponde a questa
semplice domanda: "qual è la consistenza di ciascun sottogruppo
(praticanti giovani, praticanti adulti ecc..) nel campione?". Ha scopi
puramente descrittivi. In generale si usa per confrontare un campione
con la popolazione da cui è estratto.
75
Scelta della direzione di percentualizzazione.
Di solito siamo interessati ad analizzare relazioni esplicative, da cui una
semplice regoletta:
a. si individua la variabile indipendente (la causa)
b. si usa la variabile indipendente come variabile di colonna.
c. si percentualizza per colonna.
Detto diversamente:
Si definisce qual è la variabile indipendente, e si percentualizza all'interno
delle sue modalità.
- si sceglie la percentuale per colonna quando si vuole analizzare
l'influenza che la variabile posta in colonna ha sulla variabile posta in riga;
- si sceglie le percentuale per riga quando si vuole analizzare l'influenza
che la variabile posta in riga ha sulla variabile posta in colonna.
Questa regoletta di solito funziona, ma ha delle eccezioni: a) non sempre la
domanda cui siamo interessati è esplicativa e b) non sempre è facile
individuare a colpo d'occhio la variabile indipendente (causa). E' pertanto
più opportuno partire dall'interrogativo cui vogliamo rispondere. In genere
l'interrogativo contiene già l'indicazione della direzione corretta.
Prendiamo l'esempio dell'età e della pratica religiosa: ci chiediamo se l'età
influenza la pratica religiosa. Posta in altri termini, la domanda è se i
giovani sono più o meno praticanti degli anziani. Cosa vogliamo
confrontare? Il campione dei giovani con quello degli anziani. Quindi
dobbiamo calcolare la percentuale di praticanti giovani (anziani) sul totale
dei giovani (anziani), cioè per colonna.
76
Altri esempi di percentualizzazioni di tabella a doppia entrata
Sulla base della seguente tabella a doppia entrata, stabilire se c’è una
relazione fra soddisfazione / insoddisfazione della propria situazione
economica e zona di residenza
"Secondo lei, negli ultimi 12 mesi, la situazione della sua famiglia è
migliorata, rimasta la stessa o peggiorata?”
Migliorata
Nord-ovest
Nord-est
Centro
Sud
Totale
45
17
27
56
145
Migliorata
Nord-ovest
Nord-est
Centro
Sud
Totale
31,0
11,7
18,6
38,6
100
Migliorata
Nord-ovest
Nord-est
Centro
Sud
6,5
6,0
5,7
5,4
Rimasta
uguale
445
188
308
579
1520
Peggiorata
Totale
203
78
142
408
831
693
283
477
1043
2496
Rimasta
uguale
29,3
12,4
20,3
38,1
100
Peggiorata
Rimasta
uguale
64,2
66,4
64,6
55,5
Peggiorata
Totale
29,3
27,6
29,8
39,1
100
100
100
100
24,4
9,4
17,1
49,1
100
77
A partire dalla seguente tabella a doppia entrata, effettuare gli opportuni
calcoli per poter rispondere alla domanda se esiste una relazione fra classe
sociale e fiducia nel governo
Classe operaia
Piccola borghesia
autonoma
Ceto medio impiegatizio
Ceti superiori
Totale
Per
nulla
241
166
Poco
Non so
Abbast
Molto
Totale
300
227
15
21
118
85
25
13
699
512
237
165
809
332
234
1093
22
18
76
119
77
399
14
10
62
724
504
2439
Domanda: “Quanta fiducia lei ha nell’operato del governo?”
Classe operaia
Piccola borghesia
autonoma
Ceto medio impiegatizio
Ceti superiori
Totale
Per
nulla
29,8
Poco
Non so
Abbast
Molto
27,4
19,7
29,6
40,3
20,5
29,3
20,4
100
20,8
30,4
21,4
100
27,6
28,9
23,7
100
21,3
29,8
19,3
100
21,0
22,6
16,1
100
Per
nulla
34,5
Poco
Non so
Abbast
Molto
Totale
42,9
2,1
16,9
3,6
100
44,3
45,9
46,4
4,1
3,0
3,6
16,6
16,4
15,3
2,5
1,9
2,0
100
100
100
Classe operaia
Piccola borghesia
autonoma
32,4
Ceto medio impiegatizio 32,7
Ceti superiori
32,7
78
Casi (rari) in cui non si segue il criterio sopra enunciato per la direzione
delle percentuali
Tab. 13.3 Confronti fra i profili degli abbonati
italiana nel 1991
Residenza Abbonati Popolazio Titolo di
ne
studio
Nord
27,9
26,3
Lic. Elem.
ovest
Nord est 18,9
18,3
Lic. Media
Centro
19,8
19,2
Diploma
Sud
33,4
36,2
Laurea
Totale
100
100
al telefono e dell'intera popolazione
Abbonati
Popolazione
24,2
38,0
27,7
37,4
11,7
100
35,8
21,7
4,5
100
Tab. Relazione fra pratica religiosa e comportamento di voto nel 2008 (dati fittizi)
a) Voto a seconda della pratica religiosa (come votano le persone classificate secondo
la loro religiosità)
Sinistra arc.
Pd
Udc
Pdl
Lega
Totale
(N)
Non pratic
17,4
42,9
3,5
33,1
3,0
100,0
(1132)
Saltuari
11,4
39,2
7,4
37,9
4,1
100,0
(704)
Praticanti
6,9
35,6
12,6
40,8
4,0
100,0
(522)
Totale
13,3
40,2
6,7
36,3
3,6
100,0
2358
Commento: si vede che i praticanti scelgono in maggioranza il Pdl, e i non praticanti
il Pd
b) Pratica religiosa a seconda del voto (come sono religiosamente connotati gli
elettori dei vari partiti)
Sinistra arc.
Pd
Udc
Pdl
Lega
Non pratic
62,9
51,3
25,3
43,9
40,5
Saltuari
25,6
29,1
32,9
31,2
34,5
Praticanti Totale
11,5
100,0
19,6
100,0
41,8
100,0
24,9
100,0
25,0
100,0
(N)
(313)
(948)
(158)
(855)
(84)
Commento: si vede che il partito che fra i suoi elettori la maggior presenza di cattolici
è l’Udc
79
La tabella a) risponde alla seguente domanda: "L'orientamento religioso
influenza l'orientamento di voto?" (dom. esplicativa)
La tabella b) risponde alla seguente domanda: "Sono più religiosi gli
elettori del Polo o dell'Ulivo?" (dom. descrittiva)
80
Quando si commette un grave errore
Supponiamo di essere interessati alla composizione degli elettori dell'Ulivo
secondo l'orientamento religioso a fini di propaganda elettorale. Se
usassimo la tabella a) e sostenessimo che tra gli elettori dell'Ulivo ben il
54,7% è rappresentato da Cristiani non cattolici commetteremmo un
errore. In questa tabella la percentuale di 54,7 rappresenta la quota di
cristiani che votano Ulivo, non la quota di elettori dell'Ulivo di
orientamento cristiano. L'errore consiste nel porsi un interrogativo che
richiede percentuali per riga, calcolando le percentuali per colonna (o
viceversa).
4. Analisi bivariata: presentazione delle tavole
a) prima forma di presentazione consigliata
Tab. 2.12. Grado di pratica religiosa per età. (Valori percentuali)
18-34
35-54
Oltre 54
Praticanti
24,4
27,6
41,6
Saltuari
29,1
28,0
20,1
Non praticanti
46,5
44,4
38,4
Totale
(N)
100,0
(914)
100,0
(1134)
100,0
(438)
b) seconda forma di presentazione consigliata (con il
marginale della variabile dipendente)
Tab. 2.13. Grado di pratica religiosa per età. (Valori percentuali)
18-34
35-54
Oltre 54
Totale
Praticanti
24,4
27,6
41,6
28,9
Saltuari
29,1
28,0
20,1
27,0
Non praticanti
46,5
44,4
38,4
44,1
Totale
(N)
100,0
(914)
100,0
(1134)
100,0
(438)
100,0
(2486)
81
5. Criteri guida per la presentazione delle tavole:
1. Parsimonia. La tabella deve contenere solo i dati significativi per
valutare la relazione. In genere si escludono i valori assoluti, salvo che
non si ritengano necessari. I titoli come negli esempi devono essere
sintetici, ma contenere l'indicazione delle variabili coinvolte.
2. La tabella deve contenere sempre la riga (o colonna ) totale
contenente i valori 100. Serve ad indicare in che direzione sono state
calcolate le percentuali.
3. La tabella deve contenere sempre una riga (o colonna) in cui sono
indicate le basi delle percentuali, cioè i valori assoluti corrispondenti al
100,0%. Il lettore deve sapere se i dati percentuali riguardano molti o
pochi casi.
4. I dati percentuali devono essere arrotondati alla prima cifra decimale,
come negli esempi, o arrotondati alla prima cifra intera (cioè senza
decimali). La seconda cifra decimale non si userebbe mai nei
commenti e quindi non è significativa. Le singole percentuali devono
essere arrotondate: se si usa una cifra decimale, i calcoli vanno fatti
fino alla seconda che verrà usata per gli arrotondamenti (da 0 a 4, per
difetto, da 5 a 9 per eccesso). Dopo gli arrotondamenti occorre
controllare che il totale dia effettivamente 100,0 (non 99,9 o 100,1). Se
non accade correggere il valore più alto (quadratura).
5. Se il decimale è pari a zero, va riportato ugualmente.
6. La forma della tabella 2.13 è da preferire, soprattutto se non è stata
precedentemente presentata la distribuzione di frequenza della
variabile dipendente (orientamento al voto - la colonna totale infatti
presenta tale distribuzione). Questa colonna è utile perché permette il
raffronto tra le singole colonne e il dato medio del campione.
Avvertenze: Se le percentuali sono calcolate per colonna, possono essere
sommate solo entro la colonna stessa, ma non fra le colonne. Se si
decide di accorpare due colonne bisogna sommare i valori assoluti e
solo dopo calcolare le percentuali.
82
6. Cosa fare se si vogliono ricavare i valori assoluti da una tabella che
contiene solo percentuali
L'esempio che segue mostra come si può ricavare la colonna 'Totale' in una
tabella in cui era stata omessa. Mostra indirettamente perché è importante
indicare le basi assolute delle percentuali.
Tab. 2.15 Composizione sociale degli iscritti alla facoltà di
Lettere
Maschi
Femmine
Ceti superiori
12,2
20,2
Ceti medi autonomi (art. comm.) 27,5
30,2
Ceti medi dipendenti (impiegati) 23,2
23,4
Operai
37,1
26,2
Totale
(N)
(1178)
100,0
100,0
(237)
Se si vuole ricavare la percentuale complessiva di maschi e di femmine
che proviene dai ceti superiori, occorre passare attraverso i valori assoluti:
- ricavare quanti sono i maschi dei ceti superiori
12,2 : 100 = X : 237
X = 12,2*237/100 = 29
- quante sono le femmine dei ceti superiori: (1178*20,2/100 = 238)
- sommare i due valori assoluti così ottenuti: (29+238 = 267)
- percentualizzare sul totale dei casi:
[267/(237+1178)*100 = 18,7].
83
7. Interpretazione delle tavole
Tab. 13.7. Risposte alla domanda «Lei è soddisfatto dell'operato del governo?» per
ampiezza del comune di residenza
a) valori assoluti
>250.000 100250.000
Per nulla 97
26
Poco
168
71
Non so
89
36
Abbastanza 159
66
Molto
3
2
Totale
516
201
50100.000
29
99
49
92
2
271
1050.000
23
249
118
246
8
643
1-10.000
<1.000 Totale
62
253
153
326
14
808
10
8
1
5
1
25
246
848
446
894
30
2464
Semplificazione della tabella (non si possono fare % su N < 50)
b) percentuali per colonna
>250.000 100250.000
Per nulla 18,8
12,8
Poco
32,5
35,3
Non so
17,3
18,0
Abbastanza 30,8
32,9
Molto
0,6
1,0
Totale
100
100
(N)
(516)
(201)
Idp
-17,9
-14,2
50100.000
10,8
36,5
18,0
34,0
0,7
100
(271)
-12,6
1050.000
3,5
38,8
18,3
38,2
1,2
100
(643)
-2,9
<10.000
Nulla+poco 51,3
Abb+molto 31,4
47,3
34,7
42,5
39,4
39,9
41,6
48,1
33,9
8,6
31,3
18,5
39,8
1,8
100
(833)
+1,7
Interpretazione: Si prende una modalità significativa della variabile
dipendente, e si vede come essa varia al variare della variabile
indipendente.
Commenti inutili e commenti sbagliati
Idp: Indice di differenza percentuale = soddisfatti - insoddisfatti
84
8. Forma della relazione
Tab. 13.8 Risposte alla domanda «Con che frequenza si vede con amici o
amiche, al di fuori dell'orario scolastico o di lavoro?», per età
dell'intervistato.
19-25 anni
26-35 anni
36-45 anni
46-55 anni
56-65 anni
0ltre 65
Tutti i Almeno
giorni una volta
a
settimana
41,4 52,9
15,0 67,1
8,3
66,2
4,9
54,0
10,5 43,7
23,1 35,5
Almeno
una
volta
al mese
5,7
12,1
15,2
27,6
29,3
18,8
Non ha
amici
Totale (N)
0,1
5,7
10,3
13,5
16,5
22,6
100
100
100
100
100
100
(87)
(173)
(145)
(163)
(133)
(208)
9. Presentazione compatta di tavole
Tab. 3.8 Giudizio sulla partecipazione a scioperi spontanei per età.(Valori
percentuali)
Approva
Non approva
Totale
(N)
15-19
45,2
54,8
100.0
(55)
20-29
42,1
57,9
100.0
(132)
30-29
32,8
67,2
100.0
(212)
40-49
17,7
82,3
100.0
(75)
50-59
13,1
86,9
100.0
(53)
60-69
11,8
88,2
100.0
(83)
70 e più
11,2
88,8
100.0
(62)
Tab. 3.7 - Percentuale di persone che approvano le diverse forme di azione politica
non istituzionalizzata per età.
15-19
Partecipare a scioperi spontanei 45,2
Bloccare il traffico
11,1
Fare l'autoriduz dell'affitto
18,3
Fare l'autoriduz delle bollette
19,1
Occupare case sfitte
32,2
Occupare fabbriche
33,7
Scrivere slogan sui muri
9,1
20-29
42,1
19,0
22,3
20,0
38,9
44,8
7,2
30-39
32,8
13,3
15,8
18,7
27,4
48,7
4,8
40-49
17,7
11,4
12,0
15,4
24,2
35,6
2,1
50-59
13,1
9,8
14,3
21,7
27,6
36,8
3,3
60-69 70 e più
11,8
11,2
7,9
2,2
13,9
15,8
16,3
17,7
29,2
12,1
31,9
22,7
1,0
2,3
(N)
(55) (132) (212)
(75)
(53)
(83)
Domanda: «Ora le leggerò alcune azioni che la gente talvolta fa per protestare o per
influire sul governo. Per ciascuna di queste lei mi dovrebbe dire se la approva o la
disapprova».
(62)
85
Tab. 3.9 - Il ritratto dell'elettorato italiano (percentuali di voto per diverse
variabili indipendenti; elezioni politiche del 1996).
Polo
Totale
40
Lega Ulivo Altri Totale
10
Dimensione del comune
< 10.000 ab 38 15
10-100.000
41
9
100-250.000 39
6
>250.000 ab 44
4
Genere
Maschio
39 11
Femmina
41
8
Anno di nascita
Fino al 1945 42
7
1948-1965
38
9
Dopo 1965
43 13
Classe sociale
Borghesia
57
7
Picc. borghesia41 12
Dirigenti-quadri44 6
Insegnanti
31
4
Imp. concetto 39
9
Impieg. esec. 45
9
Operai
34 14
46
4 100 (1962)
44
44
50
49
3
6
5
3
100
100
100
100
46
46
4 100 (1079)
5 100 (883)
48
48
40
3 100 (431)
5 100 (1016)
4 100 (516)
32
39
45
62
48
45
47
4
8
5
3
4
1
5
100
100
100
100
100
100
100
(654)
(808)
(189)
(313)
(195)
(275)
(170)
(188)
(392)
(240)
(493)
Polo Lega Ulivo Altri Totale
Lettura quotidiani
Lettore quot. 39
9 48
Non legge quot.42 11 43
Esposizione Tv
Alta
43 11 42
Moderata
38
9 48
Momento della decisione di voto
Ultima settim. 34 16 44
Tempo prima 43
7 46
Titolo di studio
Lic. elementare32
Lic. media
39
Diploma
44
Laurea
38
9
15
7
6
51
42
45
52
4 100 (1045)
4 100 (917)
4 100 (797)
5 100 (1148)
6 100 (502)
4 100 (1459)
8
4
4
4
100
100
100
100
(187)
(659)
(416)
(153)
86
10. Rappresentazioni grafiche
Fig. 13.1 Rappresentazioni grafiche di tavole di contingenza: diagramma a barre
a) insoddisfazione nei confronti dell'operato del governo per dimensione della città di
residenza (dati di tab. 13.7b)
Insoddisfatti
39,9
47,3
48,1
100250.000
50
50100.000
60
51,3
42,5
40
30
20
10
>250.000
10-50.000
<10.000
0
b) frequenza con la quale vede gli amici per età (dati di tab. 13.8)
45
Tutti i giorni
40
Non ha amici
35
30
25
20
15
10
5
0
19-25
26-35
36-45
46-55
56-65
0ltre 65
87
Fig. 13.3 Rappresentazioni grafiche di tavole di contingenza: spezzata
a) soddisfazione nei confronti dell'operato del governo per dimensione della città di
residenza
60
50
40
30
Insodd.
20
Sodd.
10
0
<10.000
1050.000
50100.000
100250.000
>250.000
b) frequenza con la quale vede gli amici per età
45
Tutti i giorni
40
Non ha amici
35
30
25
20
15
10
5
0
19-25
26-35
36-45
46-55
56-65
0ltre 65
88
LEZIONE 12
ANALISI BIVARIATA: DIAGRAMMA DI DISPERSIONE
ATTENZIONE: lo studente deve solo capire che cosa è un diagramma di dispersione
e come da una tabella in cui sono riportate i valori per le variabili X e Y si passa alla
rappresentazione grafica. Non è necessario che sappia calcolare i coefficienti a e b
della retta di regressione, né il coefficiente di correlazione r
Pagine di testo corrispondenti
- sul testo La ricerca sociale: metodologia e tecniche, Bologna, Il Mulino - Vol IV. L'analisi dei dati
Cap. III: par. 7.1 (solo questo sotto-paragrafo del par. 7)
- oppure sul testo Metodologia e tecniche della ricerca sociale, Bologna, Il Mulino - Cap. XIII: par.
7.1 (solo questo sotto-paragrafo del par. 7)
Tab. Voti in italiano (X) e in matematica (Y) dei 10 allievi di una classe
Caso n.
1
2
3
4
5
6
7
8
9
10
X
9
4
6
5
5
7
8
4
7
7
Y
7
4
5
5
6
8
6
3
5
6
Relazione fra i voti in italiano e in matematica degli alunni di una classe
9
8
matematica
7
6
5
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
10
italiano
89
9
8
7; 8
matematica
7
9; 7
6
5; 6
5
5; 5
4
4; 4
3
4; 3
7; 6
6; 5
8; 6
7; 5
2
1
0
0
1
2
3
4
5
6
7
8
9
10
italiano
Fig. 13.4 Diagrammi di dispersioni raffiguranti quattro tipi di relazioni fra due
variabili
a) lineare positiva (o diretta; r = 0,74)
9
8
7
6
5
4
3
2
1
0
0
2
4
6
8
10
90
b) lineare negativa (o indiretta; r = -0,81)
9
8
7
6
5
4
3
2
1
0
0
2
4
6
8
10
e) nessuna relazione (r = 0,03)
9
8
7
6
5
4
3
2
1
0
0
2
4
6
8
10
6
8
10
d) curvilinea (r = 0,06)
9
8
7
6
5
4
3
2
1
0
0
2
4
91
ESEMPIO 1
Interrogativo: nelle regioni italiane c’è una relazione fra la frequenza con la quale la
gente va al cinema e la ricchezza della regione (nelle regioni più ricche si va al
cinema di più?)
X: Ricchezza = prodotto interno lordo per abitante (in euro)
Y: Affluenza al cinema = Persone di 6 anni e più che hanno fruito del cinema per
regione di appartenenza nell’anno 2003 (valori percentuali)
Regioni
Piemonte
Valle d'Aosta
Lombardia
Trentino Alto
Adige
Veneto
Friuli Venezia
Giulia
Liguria
Emilia Romagna
Toscana
Umbria
Marche
Lazio
Abruzzo
Molise
Campania
Puglia
Basilicata
Calabria
Sicilia
Sardegna
Italia
X. Pil per
Y.
abitante (€) Affluenza(%)
25.796,60
29.952,80
28.869,90
30.430,60
48,1
40
48,5
38,7
25.796,60
26.552,50
47,6
45,3
25.511,50
28.182,40
25.137,60
22.117,10
23.080,60
27.126,90
19.109,60
18.207,40
15.642,00
15.494,00
16.077,70
15.161,90
15.854,00
18.054,60
23.114,50
46,5
48,3
50,3
45,3
48,9
52,8
48,9
41,5
52,2
47,2
42,3
35,8
47,9
42,8
48,1
Fonte: Istat, Cultura, socialità e tempo libero. Indagine multiscopo sulle famiglie “Aspetti della vita
quotidiana” Anno 2003
92
Relazione fra affluenza al cinema e prodotto
interno lordo per abitante nelle regioni italiane
55
Affluenza
50
45
40
35
30
10.000,00
15.000,00
20.000,00
25.000,00
30.000,00
35.000,00
Pil
r=0,09.
93
ESEMPIO 2
Relazione fra Pil e tasso di utilizzo del pc a livello regionale. Italia 2003.
Regioni
Piemonte
Valle d'Aosta
Lombardia
Trentino-Alto Adige
Veneto
Friuli-Venezia Giulia
Liguria
Emilia-Romagna
Toscana
Umbria
Marche
Lazio
Abruzzo
Molise
Campania
Puglia
Basilicata
Calabria
Sicilia
Sardegna
Italia
PIL1
122,0
136,1
137,4
139,3
121,5
125,1
119,2
133,7
118,0
103,3
108,2
124,3
90,8
83,4
72,1
71,6
74,9
68,5
73,1
83,4
107,9
Tasso di utilizzo
del pc
39,8
41,8
44,6
45,4
42,7
40,5
40,4
42,8
41,5
36,1
42,5
40,8
39,3
38,0
33,0
33,7
37,2
33,7
31,3
39,4
39,2
I valori dei PIL sono espressi in numeri indice, in cui la base fissa 100 è la media dei PIL dei 25 paesi dell’Unione
Europea nel 2003.
Fonte: ISTAT, Cultura, socialità e tempo libero, Roma, 2005.
Fonte per il PIL: http://www.regioni.it/mhonarc/readsqltop5.aspx
I valori dei PIL sono espressi in numeri indice, in cui la base fissa 100 è la media dei PIL dei 25 paesi dell’Unione
Europea nel 2003.
1
94
Relazione fra uso del pc e pil a livello regionale
48
46
44
Pil
42
40
38
36
34
32
30
60
80
100
120
140
160
Uso pc
r = 0,88
ESEMPIO 3
Tab. Tasso di suicidio e pratica religiosa per regione
X. % Praticanti (1)
Y. Suicidi x
100.000 ab.
Piemonte
43,3
9,3
Valle d’Aosta
26,8
14,1
Lombardia
36,5
6,7
Trentino-Alto Adige
43,0
11,5
Veneto
44,7
8,1
Friuli-Venezia Giulia
28,3
11,7
Liguria
24,6
10,7
Emilia-Romagma
26,6
9,3
Toscana
26,2
7,2
Umbria
29,5
11,3
Marche
40,8
5,9
Lazio
28,6
6,6
Abruzzo
37,4
6,7
Molise
45,5
9,0
Campania
43,2
4,0
Puglia
45,1
4,2
Basilicata
35,5
5,2
Calabria
38,8
4,6
Sicilia
43,2
5,6
Sardegna
21,2
10,3
(1) % di persone che nella regione vanno a messa tutte le settimane
Fonte: per la pratica religiosa -Indagine multiscopo sulle famiglie "aspetti della vita quotidiana"
dicembre 2001- marzo 2002, http://www.istat.it/dati/catalogo/20030708_01/
Fonte: per il suicidio –Annuario statistico 2004, http://www.istat.it/dati/catalogo/20040927_00/
95
Relazione fra pratica religiosa e suicidio per
regione
16
suicidi x 100.000 ab.
14
12
10
8
6
4
2
0
20
25
30
35
40
45
50
% praticanti
Relazione fra pratica religiosa e suicidio per
regione
16
suicidi x 100.000 ab.
14
12
10
8
R2 = 0,2474
6
4
2
0
20
25
30
35
40
45
50
% praticanti
r = – 0,50
96



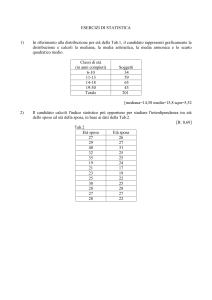

![Deliberazione [____] - Autorità per l`energia elettrica e il gas](http://s1.studylibit.com/store/data/000271583_1-c8234c3c502839ebd53a26a5bd3d2a6b-300x300.png)