Laboratorio di programmazione
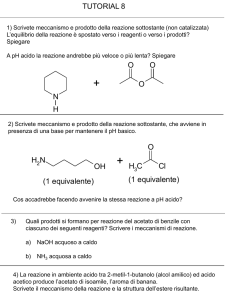
5−10 aprile 2013
Importante: Abituatevi a usare il comando
gcc -std=c99 -O -Wall -lm sorgente
oppure
gcc -std=c99 -O -Wall -lm sorgente -o eseguibile
(se volete dare un nome diverso da a.out all’eseguibile) per compilare i vostri programmi.
Ancora più importante: Le stringhe di formato della scanf devono contenere solo %d or %f. Non devono
contenere spazi, \n o quant’altro.
Tabelline
Scrivete un programma che, dopo aver richiesto in input un numero intero n, stampi la corrispondente tabellina,
moltiplicando n per i numeri interi da 1 a 10, come indicato nel seguente esempio di esecuzione:
Esempio di input
9
Esempio di output
1 x 9 = 9
2 x 9 = 18
3 x 9 = 27
4 x 9 = 36
5 x 9 = 45
6 x 9 = 54
7 x 9 = 63
8 x 9 = 72
9 x 9 = 81
10 x 9 = 90
Privo di quadrati
Un numero intero positivo è privo di quadrati se non esiste un quadrato perfetto che lo divide (equivalentemente,
se non esiste un quadrato di primo che lo divide). Scrivete un programma che legga un numero in input e determini
se è privo di quadrati.
1
Esempio di input
24
Esempio di output
24 non e’ privo di quadrati
Esempio di input
9
Esempio di output
9 non e’ privo di quadrati
Esempio di input
10
Esempio di output
10 e’ privo di quadrati
Numeri perfetti
Un numero è perfetto se è uguale alla somma dei suoi divisori propri. Per esempio, 6 = 1 + 2 + 3 è perfetto.
Scrivete un programma che, dato un intero in input, scriva i numeri perfetti minori dell’intero dato.
Esempio di esecuzione
Limite? 1000
6
28
496
Primi gemelli
Due primi p e q sono gemelli se p = q + 2. Scrivete un programma che stampi i primi gemelli minori di un intero
fornito dall’utente.
Esempio di esecuzione
Numero? 20
3 5
5 7
11 13
17 19
2
La prova del nove
La prova del nove è un meccanismo per il controllo dei calcoli basato sull’aritmetica modulare. Si basa sul fatto che
dovendo controllare se x · y = z, possiamo controllare se x · y ≡ z mod 9. Scrivete un programma che enumeri le
terne di interi x, y, z minori di un intero dato dall’utente e che stampi quelle per cui la prova del nove non funziona
(cioè x · y 6 = z ma x · y ≡ z mod 9).
Esempio di esecuzione
Limite? 5
3 3 0
3 4 3
4 3 3
Il triangolo di Tartaglia
Il triangolo di Tartaglia è un sistema per calcolare i coefficienti binomiali:
1
1
1
1
1
3
4
1
2
1
3
6
...
1
4
1
Scrivete un programma che scriva un triangolo di Tartaglia con il numero di righe richiesto dall’utente. Nella riga
n-esima, n ≥ 0, e in posizione k-esima, k ≥ 0, dovete scrivere nk . Per ottenere questo risultato, potete cominciare
ogni riga scrivendo 1, e preseguire moltiplicando per (n + 1 − k)/k (notate che questo valore è minore di uno
per certi n e k, e quindi dovete stare attenti quando effettuate la moltiplicazione). Una certa cura va posta nella
disposizione dei numeri che formano il triangolo. Ricordatevi che esiste un’opzione della direttiva di stampa %d
che permette di stampare un numero all’interno di un campo di lunghezza minima garantita.
3