Introduzione agli attuatori piezoelettrici

Università degli Studi di Bergamo
Dipartimento di Progettazione e Tecnologie
Introduzione agli attuatori
piezoelettrici
Versione 0.1
Paolo Righettini – Mauro Forlani
Introduzione agli attuatori piezoelettrici
2
Indice
1 La piezoelettricità
1.1 Materiali piezoelettrici . . . . . . .
1.1.1 Materiali presenti in natura
1.1.2 Materiali sintetici . . . . . .
1.1.3 Limitazioni . . . . . . . . .
1.2 Materiali per applicazioni . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
3
4
4
5
6
2 La normativa
2.1 Equazioni costitutive . . . . .
2.2 Equazioni della dinamica . . .
2.3 Coefficiente di accoppiamento
2.3.1 Effetto diretto . . . . .
2.3.2 Effetto inverso . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9
9
10
11
11
13
.
.
.
.
.
.
.
.
.
14
15
16
17
19
20
21
22
22
23
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Attuatori e motori piezoelettrici
3.1 Attuatori multilayer . . . . . . . . .
3.1.1 Comportamento statico . . . .
3.1.2 Amplificatori di spostamento .
3.2 Attuatori bender . . . . . . . . . . .
3.2.1 Principio di funzionamento . .
3.2.2 Comportamento statico . . . .
3.3 Motori . . . . . . . . . . . . . . . . .
3.3.1 Pulse-drive motors . . . . . .
3.3.2 Ultrasonic motors . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Introduzione agli attuatori piezoelettrici
1
3
La piezoelettricità
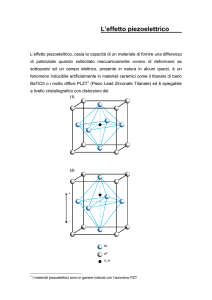
La piezoelettricità è una caratteristica naturale di alcuni cristalli che producono un campo elettrico se sottoposti ad un’azione meccanica. Il campo
elettrico è in questi cristalli il risultato della deformazione del reticolo cristallino che li costituisce: il cristallo non è più elettricamente neutro bensı̀
diviene polarizzato. Tale trasformazione è completamente reversibile.
La comparsa di un campo elettrico a causa di un’azione meccanica prende
il nome di effetto piezoelettrico diretto. Esiste anche il fenomeno opposto:
l’azione di un campo elettrico esterno provoca la deformazione del cristallo
(effetto piezoelettrico inverso). In virtù di questi due principi si possono
costruire sia sensori (effetto diretto) che attuatori (effetto inverso).
Il fenomeno della piezoelettricità è stato dimostrato sperimentalmente
per la prima volta dai fratelli Curie nel 1880. Da allora la ricerca su questo
fenomeno è cresciuta costantemente, alimentata dall’interesse per le possibili ricadute applicative. Durante la prima metà del XX secolo i maggiori
sforzi di ricerca erano concentrati nello sviluppo di trasduttori per sistemi
di navigazione (sonar ). Successivamente la ricerca si è progressivamente
estesa ai più svariati settori, dalla componentistica elettronica (filtri, generatori di frequenza, trasformatori) alle telecomunicazioni, dai beni di consumo
(accendini, stampanti a getto d’inchiostro, dischi rigidi per computer, macchine fotografiche) al settore automobilistico (sistemi di iniezione, sistemi di
controllo delle vibrazioni), dalla sensoristica (accelerometri, celle di carico,
microfoni) ai sistemi di attuazione (attuatori lineari, motori, MEMs).
1.1
Materiali piezoelettrici
I materiali piezoelettrici sono un sottogruppo dei materiali ferroelettrici i quali a loro volta fanno parte della più ampia categoria dei materiali dielettrici.
Questi ultimi sono materiali che non conducono elettricità ma interagiscono
con campi elettrici esterni. I materiali dielettrici sono infatti costituiti da
atomi parzialmente ionizzati che, per effetto di un campo elettrico esterno,
si dispongono in modo tale da contrastarne l’influenza formando dipoli elettrici; questo fenomeno prende il nome di polarizzazione. La polarizzazione
dei materiali dielettrici viene sfruttata per aumentare la capacità di accumulare cariche elettriche nei condensatori. Tra i materiali dielettrici ve ne sono
alcuni che presentano una polarizzazione intrinseca, dovuta ad una distribuzione non uniforme di cariche elettriche positive e negative, che può essere
annullata dall’applicazione di un campo elettrico esterno; questi materiali sono chiamati ferroelettrici. I materiali piezoelettrici godono quindi di tutte le
proprietà dei materiali ferroelettrici e quindi dielettrici con l’ulteriore carat-
Introduzione agli attuatori piezoelettrici
4
teristica di variare la propria polarizzazione per effetto di una deformazione
imposta e viceversa.
I materiali piezoelettrici presentano una struttura cristallina di tipo noncentrosimmetrico. Tra i 32 gruppi cristallografici i gruppi non-centrosimmetrici
sono 21; di questi 20 presentano proprietà piezoelettriche. La manifestazione
macroscopica delle proprietà piezoelettriche è dovuta sia all’intensità dell’effetto piezoelettrico che alla struttura interna del materiale. Infatti, dal punto
di vista microscopico, la struttura di un esemplare di materiale può essere
policristallina, ovvero suddivisa in più parti (dette domini di Weiss) orientate
in maniera casuale. In questo caso anche la polarizzazione dei vari domini
è orientata casualmente, per cui l’effetto piezoelettrico non si manifesta macroscopicamente (se non in maniera debole e non prevedibile). È necessario
quindi che il materiale sia costituito da un monocristallo perché manifesti
macroscopicamente le proprietà piezoelettriche.
1.1.1
Materiali presenti in natura
Nonostante la peculiarità delle caratteristiche dei materiali piezoelettrici, essi
si trovano in natura molto più frequentemente di quanto si possa pensare.
Tra quelli più comuni compaiono il quarzo, il topazio, la tormalina, il sale di
Rochelle, lo zucchero di canna, ma anche il tessuto osseo, i tendini, la dentina,
il legno e la seta. L’effetto piezoelettrico in questi materiali ha tuttavia
intensità differenti, tant’è che non tutti i materiali naturalmente piezoelettrici
trovano ricadute applicative. Degno di nota è il quarzo, con il quale sono stati
costruiti i dispositivi sonar durante la prima guerra mondiale. A causa della
ridotta intensità dell’effetto piezoelettrico nei materiali naturali, lo sviluppo
di dispositivi è rimasto a lungo confinato al campo dei trasduttori.
1.1.2
Materiali sintetici
Nel corso della seconda guerra mondiale, studi intensivi hanno portato alla
formulazione di composti che manifestano un effetto piezoelettrico molto più
intenso di quello mostrato dai materiali naturali. Tra questi composti il più
noto è una lega di piombo e ossidi di zirconio e titanio, da cui l’acronimo PZT
(legato al simbolo chimico dei suddetti elementi), largamente utilizzato per
connotare le caratteristiche di un materiale o per sottolineare la presenza di
questo tipo di materiale all’interno di un dispositivo. Nel corso degli anni si
sono sviluppati moltissimi composti che presentano proprietà piezoelettriche
calibrate sul tipo di applicazione per la quale sono stati studiati.
Introduzione agli attuatori piezoelettrici
5
Il processo di fabbricazione di un materiale sintetico è piuttosto complesso
e si compone di diverse fasi. Sommariamente il processo può essere descritto
come segue:
1. miscelazione dei vari costituenti in acqua con aggiunta di leganti, solventi e eventuali altri additivi;
2. macinazione;
3. atomizzazione (essiccamento del composto liquido mediante nebulizzazione);
4. formazione dello stampo (green body) mediante compressione del composto essiccato;
5. pre-riscaldamento finalizzato all’eliminazione degli additivi;
6. cottura in forno a temperatura inferiore alla temperatura di fusione dei
componenti;
7. esposizione del materiale sinterizzato ad un campo elettrico molto intenso per un tempo relativamente lungo a temperature elevate (poling).
Il processo di poling allinea la polarizzazione dei vari domini di Weiss
lungo la direzione del campo elettrico. Questo processo avviene ad una temperatura tale per cui tale allineamento permane anche dopo la rimozione del
campo elettrico esterno.
1.1.3
Limitazioni
I materiali piezoelettrici sono soggetti a dei limiti per quanto concerne i campi
elettrici applicati, la sollecitazione meccanica e le caratteristiche ambientali.
Il processo di poling orienta la polarizzazione dei vari domini in modo tale
che l’effetto piezoelettrico possa essere sfruttato macroscopicamente. Esistono però delle condizioni che possono variare nuovamente l’orientazione della polarizzazione degradando le caratteristiche piezoelettriche del materiale:
queste sono un aumento di temperatura o una sollecitazione di compressione eccessiva. Si verifica sperimentalmente infatti che la polarizzazione del
materiale diminuisce quadraticamente con la temperatura fino ad un valore limite (temperatura di Curie) oltre il quale la polarizzazione si annulla.
Riducendosi la polarizzazione si riduce anche l’effetto piezoelettrico, fino ad
annullarsi per temperature superiori alla temperatura di Curie. Parimenti,
una sollecitazione di compressione modifica l’orientazione dei domini e quello
Introduzione agli attuatori piezoelettrici
6
della polarizzazione: il materiale torna ad essere più simile allo stato antecedente al processo di poling. In alcuni materiali la sollecitazione modifica
solamente temporaneamente l’orientazione dei domini mentre in altri tale
deterioramento è permanente.
Accanto a questi limiti peculiari dei materiali piezoelettrici si aggiungono
le limitazioni tipiche dei materiali ceramici quali la massima sollecitazione di
trazione e di compressione (i materiali piezoelettrici sono fragili), la rigidità
elettrica (valore del campo elettrico oltre la quale vi è conduzione di corrente attraverso il materiale), la resistenza a fatica, l’aging (riduzione delle
caratteristiche piezoelettriche dovute a depolarizzazione) e la degradazione
per infiltrazione di particelle esterne (come le particelle di acqua in ambienti
umidi).
Per non oltrepassare questi limiti vengono adottate delle misure preventive quali l’impiego del materiale a temperature inferiori alla metà della temperatura di Curie, la limitazione della sollecitazione di compressione a valori
pari a circa il 25 % della sollecitazione massima ammissibile, all’impiego
di dispositivi di precarico (che impediscono stati di sollecitazione di trazione), la limitazione delle tensioni di pilotaggio e l’adozione di rivestimenti
impermeabili all’acqua.
1.2
Materiali per applicazioni
I materiali piezoelettrici per applicazioni industriali vengono divisi in tre
categorie: elettrostrittivi, soft e hard. Questi materiali si differenziano per
una serie di caratteristiche e sono classificati sulla base del valore del campo
elettrico coercivo Ec , ovvero il campo elettrico necessario all’inversione della
polarizzazione del materiale. Per valori di Ec fino a 0.1 kV/mm si parla di
materiali elettrostrittivi, per valori compresi tra 0.1 kV/mm e 1 kV/mm di
materiali soft, mentre oltre 1 kV/mm i materiali vengono detti hard.
Dal punto di vista applicativo ci sono notevoli differenze tra questi materiali. Per quanto riguarda le deformazioni indotte da campo elettrico i materiali elettrostrittivi mostrano una dipendenza apporssimativamente quadratica tra deformazione e campo elettrico, i materiali soft hanno una dipendenza
altamente non lineare tra deformazione e campo elettrico applicato per via
di una marcata isteresi1 , mentre i materiali hard, seppur simili a quelli soft,
presentano un’isteresi poco marcata (vedi figura 1).
1
L’isteresi è un fenomeno fisico per il quale la dipendenza di una grandezza da un’altra
non dipende solamente dal valore puntuale della grandezza stessa ma anche da quelli
precedenti. La rappresentazione grafica di questa dipendenza dà luogo alla tipica curva a
“farfalla”.
Introduzione agli attuatori piezoelettrici
S
S
E
elettrostrittivi
7
S
E
soft
E
hard
Figura 1: Curve S − E
Andamento qualitativo delle curve deformazione S - campo elettrico E per i differenti
materiali piezoelettrici: è evidente il fenomeno dell’isteresi. Il valore della deformazione S
non è univocamente determinato dal campo elettrico E ma anche dai valori precedenti di
deformazione.
Dal punto di vista delle deformazioni massime ottenibili indotte da un
campo elettrico, i materiali elettrostrittivi e soft hanno comportamenti simili
(valori indicativi di deformazione attorno a 0.1 %). I materiali hard invece
raggiungono valori di deformazione pari a circa la metà rispetto agli altri.
Un’importante differenza tra i vari materiali si riscontra nella loro temperatura di Curie: quella dei materiali elettrostrittivi è molto bassa (pari circa
alla temperatura ambiente) mentre i materiali soft e hard hanno temperature di Curie che in genere eccedono i 150◦ C. Tradizionalmente i materiali
hard permettevano temperature di impiego maggiori rispetto ai materiali
soft. Questa affermazione non è più cosı̀ vera in quanto sono stati sviluppati materiali soft con temperature di Curie estremamente alte (in Tab. 1
sono riportate le caratteristiche di alcuni materiali piezoelettrici commerciaR
lizzati da Physik Instrumente⃝
: si può notare come le caratteristiche varino
sensibilmente da un materiale all’altro).
Per quanto riguarda la riduzione di deformazione indotta da campo elettrico per effetto di una sollecitazione di compressione, i materiali che più ne
sono suscettibili sono i materiali elettrostrittivi. I materiali soft e hard invece
mantengono meglio questa caratteristica al crescere della sollecitazione.
Va sottolineato che i materiali piezoelettrici hanno coefficienti di espansione termica molto diversi rispetto ai metalli comunemente utilizzati in ambito
industriale. Per i materiali elencati in Tab. 1 il coefficiente di espansione
termica lineare è addirittura negativo. È bene prestare attenzione quindi
all’influenza delle variazioni di temperatura sul sistema in analisi.
La tabella Tab. 2 riassume per sommi capi le differenze che intercorrono tra i vari tipi di materiali piezoelettrici per applicazioni industriali. La
tabella è volutamente indicativa in quanto i progressi tecnologici nel campo
della ricerca dei materiali sono talmente rapidi da rendere obsolete rigide
6
-2
-2
80
4
-1
-1
6
2000
16.1
20.7
1960
1500
1780
1990
15.6
19.7
11.1
80
-12.9
27
-165
360
0.62
0.48
0.35
0.69
7.8
345
1450
1400
20
1950
1500
1750
1950
15
19
10
100
-11.5
22
2000
1420
0.62
0.47
0.35
0.69
0.66
-180
400
550
-11.3
25
0.62
0.53
0.38
0.69
-210
500
7.8
350
1750
1650
20
5
50
1960
1960
16
600
3
2270
1640
2010
2110
11.8
14.2
16.6
2000
0.56
0.46
0.32
0.66
0.63
-120
265
475
-11.2
25
-4
-2
5
2250
1610
1925
2060
12.4
13
15.8
1500
0.55
0.48
0.31
0.66
0.67
-140
310
475
-13.1
29
7.8
295
1250
1500
5
2190
1590
1550
2140
12.6
14.3
13.8
1200
0.50
0.46
0.32
0.64
0.63
-130
290
265
-9.8
21
7.8
270
1650
1550
5
2
2350
1700
1700
2100
11.1
11.8
16.4
1400
0.48
0.43
0.25
0.46
0.32
-80
155
155
-9.5
16
7.8
370
1050
950
3
141
241
300
(hard piezoelectric)
7.8
330
1200
1500
3
181
-5
-8
250
3150
2300
2500
-11.9
-50
120
0.30
0.42
0.18
15
5.5
150
950
110
(lead-free)
Caratteristiche comuni a tutti questi materiali sono la capacità termica specifica ch (350 J kg−1 K−1 ), la conduttività termica specifica ct (1.1 W m−1 K−1 ), il coefficiente di Poisson ν (0.34), i coefficienti di espansione termica nella direzione di polarizzazione e
perpendicolarmente ad essa α∥ (−4 ÷ −6 · 10−6 K−1 ) e α⊥ (4 ÷ 8 · 10−6 K−1 ) e la sollecitazione massima a compressione R (>600 MPa).
2
100
1920
2250
25
300
0.58
0.48
15
30
0.62
7.7
340
1350
152
7.6
185
4200
255
155
153
(soft piezoelectric)
7.8
250
2400
1980
20
151
R
Tabella 1: Proprietà dei materiali piezoelettrici - Physik Instrumente⃝
Physical and dielectric properties
Density
ρ
g/cm3
◦C
Curie temperature
Tc
/ε
∥ polarity
εT
33 0
Relative permittivity
⊥ polarity
εT
11 /ε0
Dielectric loss factor
tan δ
10−3
Electromechanical properties
kp
kt
Coupling factors
k31
k33
k15
d31
Piezoelectric charge constants
d33
10−12 C/N
d15
g31
Piezoelectric voltage constants
10−3 V m/N
g33
Acousto-mechanical properties
Np
N1
Frequency constants
Hz m
N3
Nt
sE
11
Elastic constants (compliance)
10−12 m2 /N
sE
33
D
Elastic constants (stiffness)
c33
1010 N/m2
Mechanical quality factor
Qm
Temperature stability
Temperature stability of εT
T
33
10−3 /K
∆εT
33 /ε33
in the range [−20 ◦ C, 150 ◦ C]
Aging stability relative change of the parameter
Relative dielectric constant
cε
%
Coupling factor
cK
Material type
Introduzione agli attuatori piezoelettrici
8
Introduzione agli attuatori piezoelettrici
Materiale
Isteresi
Temp. Curie
Deformazione
elettrostrittivo
BASSA
BASSA
ALTA
9
soft
ALTA
MEDIO-ALTA
ALTA
hard
MEDIA
MEDIA
MEDIA
Tabella 2: Tabella riepilogativa
classificazioni.
2
La normativa
Esiste un documento di riferimento per l’analisi e la caratterizzazione dei
materiali piezoelettrici: questo è la normativa ANSI/IEEE Std 176-1987. In
questa normativa vengono illustrate la teoria lineare della piezoelettricità e la
cristallografia dei materiali piezoelettrici, vi sono richiami di teoria delle onde
piane. Inoltre vengono ricavate delle formulazioni specifiche per alcuni tipi di
geometrie come dischi, lastre piane e barre nelle diverse modalità di funzionamento. Infine viene illustrata una modalità di prova per la determinazione
delle costanti piezoelettriche.
Un’altra importante norma nell’ambito dei materiali piezoelettrici è la direttiva RoHS (Restriction of Hazardous Substances). Questa direttiva elenca
una serie di materiali il cui impiego in apparecchiature elettriche ed elettroniche è soggetto a vincoli. Questi materiali sono il piombo, il mercurio, il
cadmio, il cromo esavalente, i bifenili polibromurati e l’etere di difenile polibromurato. Allo stato attuale, l’utilizzo di materiali piezoelettrici contenenti
piombo è ammesso.
2.1
Equazioni costitutive
Le equazioni costitutive di un materiale sono delle relazioni che legano diverse grandezze rappresentative dello stato del materiale stesso. Nel caso della
teoria lineare della piezoelettricità le grandezze di interesse sono la deformazione S, la sollecitazione meccanica T , il campo elettrico E e l’induzione
elettrica D. La deformazione e la sollecitazione sono grandezze tensoriali del secondo ordine mentre il campo elettrico e l’induzione elettrica sono
grandezze vettoriali. Le relazioni che legano le varie grandezze sono:
Tij = cE
ijkl Skl − eijk Ek
Di = eijk Skl + εSij Ek
(1)
Introduzione agli attuatori piezoelettrici
Indice tensoriale (ij,kl)
Indice matriciale (p,q)
11
1
22
2
10
33
3
23,32
4
31,13
5
12,21
6
Tabella 3: Tabella di conversione degli indici
dove cE
ijkl è la costante elastica, eijk è la costante piezoelettrica di carica e
εSij è la permettività dielettrica2 ; gli indici variano da 1 a 3. Queste equazioni consentono di studiare un materiale piezoelettrico di geometria definita
solamente dal punto di vista statico.
Per semplificare l’aspetto formale delle equazioni costitutive, viene introdotta una simbologia che consente di ridurre il numero degli indici. Secondo
lo schema indicato in Tab. 3, i tensori sollecitazione e deformazione vengono
scritti come vettori, mentre i tensori di ordine superiore vengono ridotti a
matrici. Le equazioni costitutive di Eq. 1 vengono quindi riscritte come:
{
Tp = cE
pq Sq − ekp Ek
(2)
Di = eiq Sq + εSik Ek
Bisogna prestare però attenzione al fatto che le relazioni cosı̀ scritte non
godono più delle proprietà dei tensori (ovvero l’invarianza rispetto al sistema
di riferimento prescelto).
2.2
Equazioni della dinamica
Le equazioni della dinamica per un materiale piezoelettrico sono piuttosto
complesse, trattandosi di un sistema di equazioni alle derivate parziali del
secondo ordine:
{ E
cijkl uk,li + ekij φ,ki = ρu,τ τ
(3)
eijk ui,jk − εSij φ,ij = 0
dove ρ è la densità del materiale, u è lo spostamento dalla configurazione
iniziale, φ il potenziale elettrico e τ il tempo3 . Valgono inoltre le seguenti
relazioni:
2
L’apice presente nelle costanti elastiche e dielettriche indica la condizione alla quale
tali costanti sono state misurate. Nell’equazione 1, la costante elastica è misurata a campo
elettrico costante, mentre la permettività elettrica a deformazione costante.
3
La derivata parziale di una variabile segue qui la notazione della virgola. Ad esempio:
uk,li =
∂ 2 uk
∂xl ∂xi
Introduzione agli attuatori piezoelettrici
{
11
Ek = −φ,k
Skl = uk,l
(4)
che legano il campo elettrico al potenziale e la deformazione agli spostamenti. Per un problema monodimensionale come quello di una lastra sottile
soggetta a sforzi e deformazioni perpendicolari al piano della lastra stessa le
equazioni 3 e 4 assumono la seguente forma semplificata:
{ E
c u,xx + eφ,xx = ρu,τ τ
(5)
eu,xx − εS φ,xx = 0
{
Ex = −φ,x
(6)
Sx = u,x
I due sistemi di equazioni possono essere combinati ottenendo cosı̀ la
seguente forma compatta:
u,xx =
cE
ρ
+
e2
εS
u,τ τ
(7)
che altro non è che l’equazione di propagazione di un’onda piana in un mezzo
solido. La velocità di propagazione dell’onda nella lamina piezoelettrica è pari
a:
√
2
cE + εeS
v=
(8)
ρ
2.3
Coefficiente di accoppiamento
Il fenomeno della piezoelettricità consente di convertire energia meccanica
in energia elettrica e viceversa. Mediante l’effetto diretto il lavoro compiuto
della forza di compressione viene convertito in energia di deformazione e
in energia elettrica, mentre grazie all’effetto inverso energia elettrica viene
in parte trasformata in energia di deformazione e in parte accumulata nel
materiale.
Si consideri una lamina sottile di materiale piezoelettrico il cui spessore t
sia molto inferiore rispetto alle dimensioni trasversali; l’area complessiva della
lamina sia pari ad A. Sulle facce superiore ed inferiore della lamina sono
applicati due elettrodi che possono essere connessi o disconnessi ad un circuito
elettrico in grado di fornire una differenza di potenziale e di assorbire una
corrente proveniente dagli elettrodi.
Introduzione agli attuatori piezoelettrici
R
f
12
R
(a)
f
(b)
Figura 2: Lamina piezoelettrica collegata ad un circuito elettrico passivo
2.3.1
Effetto diretto
Applicando una forza omogenea sugli elettrodi il materiale piezoelettrico è
uniformemente sollecitato meccanicamente. Nel caso un cui il circuito elettrico sia chiuso (vedi figura 2.a), il campo elettrico nella lamina deve essere
necessariamente nullo, in quanto non vi è accumulo di cariche. In questo
caso le equazioni costitutive (Eq. 2) si scrivono come:
{
S = c1E f
(9)
D = ceE f
dove la sollecitazione T è pari a f . Il lavoro della forza per unità di volume
può essere calcolato come:
1 2
f
(10)
2cE
Nel caso in cui la lamina sia scollegata dal circuito elettrico, il campo
elettrico non è nullo bensı̀ sarà nullo lo spostamento elettrico (vedi figura 2.b).
Le equazioni costitutive assumono la forma:
{
εS
S = e2 +c
E εS f
(11)
E = − e2 +ceE εS f
uE
m =
mentre la sollecitazione T è sempre pari a f . Dal punto di vista meccanico il
materiale piezoelettrico appare più rigido se scollegato dal circuito elettrico,
come si evince dalle differenti deformazioni indotte dalla forza esterna (Eq. 9
e Eq. 11). Il lavoro della forza per unità di volume può essere calcolato come:
uD
m =
εS
f2
2
E
S
2 (e + c ε )
(12)
D
È importante notare come uE
m > um in quanto nel secondo caso parte
dell’energia meccanica in ingresso viene convertita in energia elettrica. Infatti
vi è un accumulo pari a
Introduzione agli attuatori piezoelettrici
Vs
13
Vs
(a)
(b)
Figura 3: Lamina piezoelettrica collegata ad una sorgente di tensione
D
ue = uE
m − um =
e2
f2
2cE (e2 + cE εS )
(13)
Il coefficiente di accoppiamento elettromeccanico per una lamina sottile
eccitata nello spessore è pari a
√
√
u
εS cE
e
e
t
(14)
k33
=
=
1
−
=√
E
2
S
E
um
e +ε c
εS cD
33
dove, per l’ottenimento della formula di Eq. 14, sono state impiegate le
relazioni tra i coefficienti e, εS e cE riportate in [2].
2.3.2
Effetto inverso
Il coefficiente di accoppiamento elettromeccanico può essere calcolato anche
immettendo energia elettrica nel sistema. Si supponga quindi di connettere
gli elettrodi ad una sorgente di tensione lasciando liberamente deformare la
lamina piezoelettrica (vedi figura 3.a). In questo caso le equazioni costitutive
(Eq. 2) si scrivono come:
{
e Vs
S = − c(
E t
)
(15)
e2
S Vs
D = − cE + ε
t
dove la sollecitazione T è nulla. L’energia accumulata coincide con l’energia
accumulata elettricamente, la quale, per unità di volume, può essere calcolata
come:
(
) ( )2
1 e2
Vs
S
T
+ε
(16)
ue =
E
2 c
t
Analogamente a quanto fatto in precedenza, si può di seguito calcolare
l’energia elettrica introdotta nel caso in cui alla lamina sia impedito di deformarsi liberamente (vedi figura 3.b). Le equazioni costitutive assumono la
forma:
Introduzione agli attuatori piezoelettrici
{
T = −e Vts
D = −εS Vts
L’energia accumulata elettricamente è pari a:
( )2
1 S Vs
S
ue = ε
2
t
14
(17)
(18)
È importante notare come uTe > uSe in quanto nel secondo caso parte
dell’energia elettrica in ingresso viene convertita in energia meccanica. Infatti
vi è un accumulo pari a
( )2
1 e2 Vs
T
S
um = u e − u e = E
(19)
2c
t
Il coefficiente di accoppiamento elettromeccanico per una lamina sottile
eccitata nello spessore è pari a
√
√
um
e2
e
t
√
(20)
k33 =
=
=
uTe
e2 + ε S c E
εS c D
33
dove, per l’ottenimento della formula di Eq. 20, sono state impiegate le relazioni tra i coefficienti e, εS e cE riportate in [2]. Si noti che le due metodologie
di calcolo hanno fornito gli stessi risultati (Eq. 14 e Eq. 20).
3
Attuatori e motori piezoelettrici
Gli attuatori e i motori piezoelettrici sfruttano l’effetto piezoelettrico inverso
convertendo energia elettrica (tensione e corrente) in energia meccanica (forze
e spostamenti). Gli attuatori propriamente detti sono dei dispositivi che si
presentano monolitici (Solid-State Actuators) mentre i motori sono costituiti
da più parti. Le tipologie di attuatore maggiormente diffuse sono gli attuatori
multilayer (MLA) e gli attuatori bender.
Gli attuatori multilayer e bender realizzano il massimo spostamento in
corrispondenza della massima tensione di alimentazione, mentre i motori
piezoelettrici compiono uno spostamento estremamente ridotto in corrispondenza di una serie determinata di impulsi di tensione. La ripetizione ad alta
frequenza di questa serie di impulsi consente di ottenere spostamenti lineari
o rotativi più ampi. L’ampiezza degli spostamenti lineari è limitata dalla
dimensione del supporto fisico con il quale il motore si interfaccia.
Nonostante l’effetto piezoelettrico inverso consista nella generazione di
una deformazione per effetto di un campo elettrico, gli attuatori e i motori
Introduzione agli attuatori piezoelettrici
15
Vs
Figura 4: Disposizione delle lamine e cablaggio in un attuatore multilayer
piezoelettrici non sono generatori di moto ideali. Infatti la forza che gli
attuatori forniscono per realizzare uno spostamento induce delle deformazioni
e quindi degli spostamenti di segno opposto rispetto a quelli desiderati. I
motori sono soggetti a delle limitazioni sulla forza di attuazione legate invece
al fenomeno dell’attrito tra superfici.
3.1
Attuatori multilayer
Un attuatore piezoelettrico multilayer è costituito da una serie di lamine
piezoelettriche impilate una sopra l’altra e racchiuse tra due elettrodi. Per
un’ottimizzazione delle dimensioni e del numero di componenti, tra due lamine adiacenti vi è un solo elettrodo: i campi elettrici generati dalla differenza di
potenziale applicata agli elettrodi, perpendicolari alle lamine, cambiano quindi verso ad ogni strato. Perché le deformazioni indotte si sommino in maniera
costruttiva le lamine piezoelettriche adiacenti devono avere polarizzazione di
verso alterno (vedi figura 5).
In un attuatore MLA la tensione applicata induce una deformazione nella
direzione delle linee di campo elettrico, perpendicolari al piano della lamina. Questa modalità di funzionamento è generalmente denominata 33 (il
campo elettrico nella direzione 3 induce una deformazione nella direzione 3).
Il campo elettrico è costante nello spessore della lamina, quindi anche la
deformazione indotta è omogenea.
Dal punto di vista elettrico, un attuatore MLA si comporta come un
carico capacitivo fintanto che le condizioni operative sono lontane dalle frequenze di risonanza. Ciascuno strato con i relativi elettrodi costituisce infatti
un condensatore la cui capacità, in condizioni statiche, può essere calcolata
come:
Introduzione agli attuatori piezoelettrici
16
A
(21)
t
dove A e t sono rispettivamente area degli elettrodi e spessore dello strato
di materiale piezoelettrico. Dato che gli elettrodi sono collegati in parallelo
alla sorgente di tensione (vedi figura 4) anche la capacità risultante di un
attuatore formato da L strati si calcola sommando i singoli contributi:
C0j = εS
C0 =
L
∑
j=1
3.1.1
C0j = LεS
A
t
(22)
Comportamento statico
Si supponga di testare il comportamento statico di un attuatore MLA soggetto ad una forza costante che si oppone al moto (vedi figura 5). L’attuatore
non soggetto a forze esterne e con tensione di alimentazione nulla presenta una lunghezza nominale H. Senza variare la tensione di alimentazione e
applicando una forza di compressione F , si verifica che la lunghezza dell’attuatore si riduce di una quantità proporzionale alla forza. Applicando ora
una tensione Vs l’attuatore si deforma allungandosi; l’entità della deformazione dipende dal valore di tensione applicata. Le equazioni costitutive per
un singolo strato si possono scrivere come:
{
{
S = − c1E f + tc(eE Vs
−f = cE S + e −Vt s
)
2
⇒
(23)
D = eS − εS −Vt s
D = − ceE f + ceE + εS Vts
dove f = FA . Lo spostamento complessivo dell’estremo libero dell’attuatore
può quindi essere calcolato come:
(
)
t
e
u = − E f + E Vs L
(24)
c
c
Il comportamento statico di un attuatore piezoelettrico può essere riassunto graficamente. La figura 6.a mostra l’andamento delle curve di spostamento u(Vs ) al variare del valore della tensione di alimentazione Vs per
differenti valori della forza F mentre la figura 6.b mostra il luogo dei valori di spostamento massimo umax (F ) al variare della forza F per differenti
valori della massima tensione di alimentazione Vs,max . Al crescere della tensione di alimentazione Vs aumenta anche lo spostamento, la pendenza della
retta u(Vs ) è pari a L ceE , mentre il punto di intersezione con l’asse delle
ordinate è −L ctE f . La presenza di una forza costante induce una deformazione e quindi uno spostamento di segno opposto, introducendo un “offset”
Introduzione agli attuatori piezoelettrici
17
F
F
0V
0V
Vs
Figura 5: Attuatore multilayer soggetto ad una forza costante di
compressione
di spostamento negativo a tensione di alimentazione nulla. Lo spostamento
complessivo ottenuto quindi alimentando l’attuatore piezoelettrico alla massima tensione di alimentazione non varia al variare della forza esterna, purché
sia costante. Lo spostamento massimo indicato in figura 6.b è misurato rispetto alla condizione di tensione di alimentazione e forza esterna nulle. Il
ruolo dei termini di forza e spostamento in questo grafico viene invertito e
quindi la pendenza della retta umax (f ) è pari a −L ctE , mentre il punto di
intersezione con l’asse delle ordinate è L ceE Vs,max . In questa trattazione si è
supposto per semplicità che tra le varie grandezze vi siano relazioni lineari.
3.1.2
Amplificatori di spostamento
Gli attuatori multilayer, nonostante consentano con la loro configurazione
seriale di ottenere spostamenti più ampi mantenendo basse tensioni di alimentazione, hanno corse massime pari a circa lo 0.1 % della loro lunghezza.
A fronte di ciò, la forza che gli attuatori MLA sono in grado di sviluppare
è molto elevata; il valore massimo di questa forza è legato a questioni di carattere strutturale. Genericamente si suole limitare la sollecitazione massima
sul materiale piezoelettrico al 5-10 % del valore di rottura. Dato che, per evitare condizioni di instabilità, la pila di lamine piezoelettriche non può essere
eccessivamente snella e dato che la sollecitazione ammissibile è elevata (circa 30 MPa per i materiali in Tab. 1), le forze massime agenti sull’attuatore
sono molto elevate. In alcune applicazioni può essere conveniente convertire
i rapporti di forza e spostamento mediante l’introduzione di un meccanismo
che amplifichi gli spostamenti a discapito delle forze di attuazione.
Introduzione agli attuatori piezoelettrici
u
18
umax
Vs
F
F
Vs,max
(6.a)
(6.b)
Figura 6: Andamento spostamento - tensione al variare della forza esterna
applicata (a) e spostamento massimo in funzione di forza esterna e tensione
massima di alimentazione (b)
MLA
@
@
@
@
braccio
(7.a)
interfacce
(7.b)
Figura 7: Cedrat - APA 40 SM (a) e relativo modello schematico (b)
Introduzione agli attuatori piezoelettrici
19
7
6
5
τ [−]
4
3
2
1
0
5
10
15
20
25
30
α0 [deg]
Figura 8: Andamento del rapporto di trasmissione τ al variare di α0 .
A titolo di esempio si riporta l’analisi di un attuatore attualmente in
commercio dotato di un meccanismo di amplificazione degli spostamenti (Cedrat APA 40 SM [3], vedi figura 7.a). Questo attuatore è costituito da un
attuatore MLA inserito in un telaio metallico. Il telaio costituisce un meccanismo deformabile la cui schematizzazione a corpi rigidi è mostrata in figura 7.b. Una variazione di lunghezza dell’attuatore piezoelettrico si traduce in
una variazione della distanza tra le interfacce. Definendo l la lunghezza del
braccio e α0 l’angolo iniziale formato tra l’asse dell’attuatore e di un braccio
il rapporto di trasmissione può essere espresso come:
(
(
umax )))
− sin α0 + sin arccos cos α0 +
(25)
umax
2l
In figura 8 è rappresentato il valore del rapporto di trasmissione al variare
dell’angolo α0 . Dato che il rapporto umax /l è sempre molto piccolo per via
delle limitate deformazioni, il rapporto di trasmissione ne è praticamente
indipendente. All’aumentare di α0 il rapporto di trasmissione diminuisce.
Questo meccanismo è quindi in grado di amplificare il moto dell’attuatore
MLA in maniera decisamente marcata per piccoli valori dell’angolo α0 .
Bisogna sottolineare però che questo meccanismo di amplificazione del
moto inverte la direzione dello spostamento. Ad un’espansione dell’attuatore
corrisponde una diminuzione della distanza tra le interfacce e viceversa.
τ=
2l (
Introduzione agli attuatori piezoelettrici
3.2
20
Attuatori bender
Gli attuatori bender sono delle lamine multistrato che si flettono per effetto
del campo elettrico indotto dalla tensione di alimentazione. Questi attuatori
sono costituiti da una serie di lamine piezoelettriche sottili incollate fra di
loro. Le configurazioni possibili, seppur numerose, fanno riferimento a due
schemi base: unimorfo e bimorfo (vedi figura 9). L’attuatore unimorfo è
costituito da una lamina piezoelettrica e da uno strato passivo di materiale
(genericamente metallico). L’attuatore bimorfo invece presenta uno strato
centrale di materiale passivo sulle cui superfici superiore e inferiore vengono
incollati due strati di materiale piezoelettrico. L’attuatore bimorfo presenta
delle varianti a seconda delle quali può mancare lo strato intermedio passivo
oppure possono esserci più di due strati di materiale piezoelettrico (bender
multilayer).
Gli elettrodi sono applicati sulle superfici superiore e inferiore di ciascuno
strato piezoelettrico. Lo strato passivo genericamente funge anche da elettrodo. Mentre per l’attuatore unimorfo vi è una sola possibilità di cablaggio,
per l’attuatore bimorfo esistono due modalità, come mostrato in figura 10.
La differenza sostanziale tra le due sta nel numero di elettrodi necessari e
come conseguenza nell’intensità del campo elettrico rispetto alla tensione di
alimentazione.
3.2.1
Principio di funzionamento
Il principio di funzionamento degli attuatori bender si basa sull’induzione di
uno stato di deformazione che ricalca quello di una trave soggetta a flessione
pura. Una trave cosı̀ sollecitata presenta momento flettente costante in ogni
sua sezione; la distribuzione della sollecitazione all’interno della sezione è
“a farfalla”, ovvero le sollecitazioni sono positive sul lato delle fibre tese,
negative sul lato delle fibre compresse e variano linearmente tra questi due
estremi annullandosi in corrispondenza dell’asse neutro. Nell’ipotesi che lo
stato di sforzo sia piano, le deformazioni indotte hanno la stessa distribuzione.
layer PZT
elettrodo
layer passivo
Unimorfo
Bimorfo
Figura 9: Possibili configurazioni per attuatori bender
Introduzione agli attuatori piezoelettrici
21
Vs
Vs
Figura 10: Disposizione delle lamine e cablaggio in un attuatore bender
Il campo elettrico applicato alle lamine piezoelettriche induce una deformazione normale sia nello spessore (modo 33, come nel caso degli attuatori
MLA) che perpendicolarmente ad esso (modo 31), tendendo ad allungare le
fibre nel piano della lamina. L’allungamento delle fibre nel piano della lamina è in realtà ostacolato o dallo strato passivo, che non ha variazioni di
lunghezza, o dal secondo strato piezoelettrico, che subisce una deformazione di segno opposto. In entrambi i casi le deformazioni indotte da campo
elettrico portano ad una flessione dell’attuatore.
3.2.2
Comportamento statico
Le equazioni costitutive per l’attuatore bender sono in maggior numero rispetto all’attuatore MLA per prendere in considerazione le deformazioni e le
sollecitazioni nelle tre direzioni:

T1 = cE

11 S1 − e31 E3


E
T2 = c11 S2 − e31 E3
(26)
E
T

3 = c33 S3 − e33 E3


D3 = e31 (S1 + S2 ) + e33 S3 + εS33 E3
dove 1 è la direzione assiale, 3 è quella nello spessore e 2 è perpendicolare
alle prime due. Al contrario del caso dell’attuatore multilayer, in cui la
sollecitazione e la deformazione sono costanti in tutto il materiale, in questo
caso lo stato di sollecitazione è variabile da nello spessore e nella lunghezza.
Lo stato di sollecitazione risultante è una combinazione dell’azione del campo
elettrico e della deformazione dell’attuatore.
Introduzione agli attuatori piezoelettrici
22
La deformazione statica di un attuatore bender bimorfo costituito da due
lamine piezoelettriche di lunghezza l e uguale spessore t può essere calcolata
come [1]:
δ=3
e31 l2
V
2 s
cE
11 t
(27)
Una forza esterna applicata induce uno stato di sollecitazione che va a
sommarsi a quello dovuto all’effetto piezoelettrico inverso. Data la linearità
delle equazioni vale il principio di sovrapposizione degli effetti.
3.3
Motori
I motori piezoelettrici sono dei dispositivi che, grazie ad un piccolo movimento relativo di due o più parti generato per effetto piezoelettrico inverso,
sono in grado di realizzare spostamenti su ampia scala. Nonostante esista
una grande varietà di principi di funzionamento e configurazioni, è possibile
ricondurre la tipologia costruttiva a due grandi categorie: motori pilotati
con segnali impulsivi (pulse-drive motors) e motori ultrasonici (ultrasonic
motors).
I motori piezoelettrici consentono di ottenere rendimenti maggiori rispetto
ai corrispondenti motori elettromagnetici quando le dimensioni complessive
del dispositivo diminuiscono. Infatti l’efficienza del materiale piezoelettrico
non è influenzata da fattori di scala.
3.3.1
Pulse-drive motors
I pulse-drive motor sono motori costituiti da una serie di attuatori piezoelettrici che vengono pilotati con un segnale di tipo on/off. Per esemplificare
il funzionamento di tali dispositivi si consideri il meccanismo a inchworm
rappresentato in figura 11. Il motore è costituito da una parte fissa e da una
parte mobile formata da tre attuatori piezoelettrici (parti 1, 2 e 3). L’attuatore 1 è responsabile della traslazione mentre gli attuatori 2 e 3 vincolano la
parte mobile a quella fissa.
Un’opportuna sequenza di segnali di pilotaggio consente una traslazione
lungo la parte fissa. Le operazioni che costituiscono un ciclo completo per
realizzare un passo sono:
1. l’attuatore 2 è attivato, mentre il 2 e il 3 sono disattivati;
2. l’attivazione dell’attuatore 1 comporta un allungamento della parte mobile;
3. l’attuatore 3 si è spostato e viene attivato perché mantenga tale posizione;
Introduzione agli attuatori piezoelettrici
23
2 1 3
τ1
V1
τ2
τ1 τ2 τ3 τ4 τ5 τ6 τ7
τ
τ1 τ2 τ3 τ4 τ5 τ6 τ7
τ
τ1 τ2 τ3 τ4 τ5 τ6 τ7
τ
τ3
V2
τ4
τ5
τ6
V3
τ7
Figura 11: Motore inchworm e segnali di pilotaggio
4. l’attuatore 3 viene disattivato perché possa avanzare;
5. l’attuatore 1 viene disattivato e torna alla lunghezza iniziale facendo avanzare l’attuatore 2;
6. l’attuatore 2 viene attivato perché mantenga tale posizione;
7. l’attuatore 3 viene disattivo e la parte mobile si trova nella configurazione
iniziale.
La velocità che la parte mobile raggiunge non dipende dalla velocità alla quale l’attuatore si espande bensı̀ alla frequenza con la quale il ciclo di
operazioni viene ripetuto. Va notato come la velocità del motore sia completamente regolabile tra zero e un valore massimo pari a τu7max
. La forza di
−τ1
attuazione che questi motori sono in grado di generare dipende largamente
dalle forze di attrito che nascono dal contatto tra gli attuatori 2 e 3 e la parte
fissa.
La configurazione illustrata prevede una parte mobile attuata e una parte
fissa passiva; esistono numerose altre configurazioni in cui i ruoli sono invertiti. È inoltre possibile che il moto ottenuto sia rotativo invece che lineare. A
seconda delle modalità costruttive i pulse-drive motor possono non necessitare tensione di alimentazione per mantenere la propria posizione, come invece
è necessario nel caso mostrato.
Introduzione agli attuatori piezoelettrici
24
traiettoria del
punto di contatto
PZT
componente elastico
parte mobile
Figura 12: Standing Wave Motor
3.3.2
Ultrasonic motors
I motori ultrasonici sono composti da una parte vibrante (a sua volta costituita da un componente piezoelettrico e un componente elastico) e da una
parte mobile (in genere un componente elastico con opportuno rivestimento
superficiale). Sfruttando le proprie frequenze di risonanza, la parte vibrante imprime per attrito il moto alla parte mobile. Tipicamente il punto di
contatto della parte vibrante con la parte mobile realizza un movimento periodico di tipo ellittico; il contatto dura però solo per una frazione del periodo,
imprimendo un moto unidirezionale.
Con riferimento alla figura 12, l’elemento piezoelettrico vibrando assialmente eccita un modo di vibrare flessionale dell’elemento elastico. La combinazione dei due moti è tale per cui un punto dell’elemento elastico compie
una traiettoria ellittica. Lo spostamento assiale consente il contatto tra le
due parti mentre la deformazione flessionale imprime uno spostamento alla
parte mobile.
Il principio di funzionamento illustrato è tipico dei motori Standing Wa-
Introduzione agli attuatori piezoelettrici
25
ve, ovvero quei motori che imprimono un moto periodico ad loro una parte
mediante una sorgente di vibrazioni (l’attuatore piezoelettrico). Altri motori, detti Surface Wave o Travelling Wave, si basano invece sul generazione
di due moti periodici tra loro sfasati di 90◦ sia nel tempo che nello spazio.
Questa soluzione consente di variare anche la direzione del moto. Entrambe
le soluzioni consentono di ottenere un moto sia rotativo che lineare.
A dispetto dei pulse-drive motor, i motori ultrasonici non consentono una
regolazione della velocità cosı̀ ampia come quella offerta dai primi. Infatti
è necessario eccitare una frequenza di risonanza perché questi dispositivi
funzionino, il che vincola anche le velocità di funzionamento.
Riferimenti bibliografici
[1] Kenji Uchino. Piezoelectric Actuators and Ultrasonic Motors. Kluwer
Academic Publishers, 1987.
[2] ANSI/IEEE Std 176-1987.
[3] Cedrat group http://www.cedrat.com.