PROGETTO RETI DI TELECOMUNICAZIONI
13/05/2005
Esercizio 1
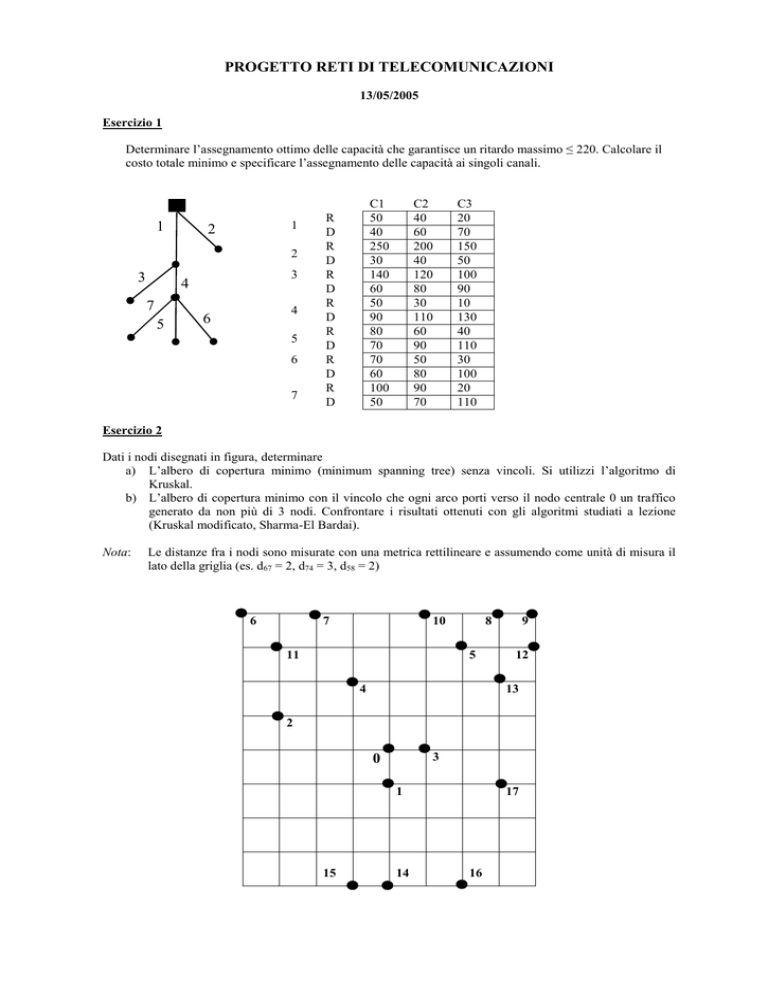
Determinare l’assegnamento ottimo delle capacità che garantisce un ritardo massimo ≤ 220. Calcolare il
costo totale minimo e specificare l’assegnamento delle capacità ai singoli canali.
1
1
2
2
3
3
4
7
5
4
6
5
6
7
C1
50
40
250
30
140
60
50
90
80
70
70
60
100
50
R
D
R
D
R
D
R
D
R
D
R
D
R
D
C2
40
60
200
40
120
80
30
110
60
90
50
80
90
70
C3
20
70
150
50
100
90
10
130
40
110
30
100
20
110
Esercizio 2
Dati i nodi disegnati in figura, determinare
a) L’albero di copertura minimo (minimum spanning tree) senza vincoli. Si utilizzi l’algoritmo di
Kruskal.
b) L’albero di copertura minimo con il vincolo che ogni arco porti verso il nodo centrale 0 un traffico
generato da non più di 3 nodi. Confrontare i risultati ottenuti con gli algoritmi studiati a lezione
(Kruskal modificato, Sharma-El Bardai).
Nota:
Le distanze fra i nodi sono misurate con una metrica rettilineare e assumendo come unità di misura il
lato della griglia (es. d67 = 2, d74 = 3, d58 = 2)
6
7
10
11
8
5
4
9
12
13
2
3
0
1
15
14
17
16
Esercizio 3
È data una rete definita da un grafo G=(V,E), e una capacità cij su ogni arco {i,j}. Un insieme Q di
domande di traffico (sq,tq,vq) devono essere instradate tra coppie sorgente-destinazione (sq,tq). Al fine di
rendere la rete stabile rispetto a possibili guasti, si vuole che ogni domanda sia instradata su almeno k
cammini che non condividono alcun link tra di loro. Quindi il volume vq di ogni domanda di traffico verrà
scomposto in almeno k “sotto-flussi”, che portano una frazione di vq e tali che comunque il flusso totale
inviato sia pari a vq. Si ammette che in un nodo intermedio due sotto-flussi possano mischiarsi e lasciare il
nodo in proporzioni diverse, ma si richiede che ogni sottoflusso porti una quantità di traffico pari a vq/2k.
-
Qual’è il minimo e il massimo numero di sotto-flussi su cui viene instradato il traffico?
Formulare un modello di Programmazione Lineare Intera che permetta di minimizzare la
congestione
v ( f
qQ
-
q
massima
sui
link
della
rete,
ovvero
v ( f
qQ
q
ij
q
q
ij
f jiq ) cij , dove
f ) cij (suggerimento: usare, per ogni arco orientato, una variabile continua ed
q
ji
una binaria).
Formulare il modello con variabili di cammino anziché di flusso. Quanti vincoli e variabili
contiene questo modello e quanti quello con variabili di flusso?
Come cambia il modello se si vuole massimizzare la minima frazione di volume instradato?
Esercizio 4
Su una rete definita da un grafo G=(V,E) dobbiamo instradare un insieme Q di domande di traffico
(sq,tq,vq) tra coppie sorgente-destinazione (sq,tq). Si deve stabilire quanta capacità installare sui link della
rete in modo che tutte le domande siano instradate e il costo della rete sia minimo. Per ogni domanda si
richiede che esista un solo cammino da sorgente a destinazione. Si supponga che ogni link {i,j} abbia un
costo per unità di traffico pari a dij. Inoltre, tutti i nodi hanno capacità massima pari a C1 ma sono
disponibili p apparecchiature che, se installate (non più di una per nodo) danno ciascuna una capacità
aggiuntiva pari a C2.
-
Formulare un modello di Programmazione Lineare Intera che permetta di minimizzare il costo
della rete definita dal costo delle capacità di link installate.
Supponendo che queste apparecchiature abbiano un costo D e volendo includere nel costo totale
anche il loro costo, come cambia il modello?
Definire un algoritmo di ricerca locale per il problema, supponendo che sia disponibile una
soluzione dove non si possa togliere da un nodo i alcuna apparecchiatura aggiuntiva senza
cambiare l’instradamento delle domande che passano per i.












