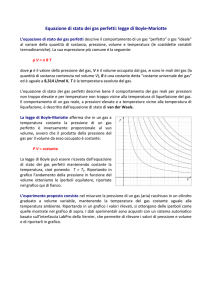
1. Si ha f (x) = g 0 (x). Sapendo che Γ è tangente all'asse delle ascisse nell'origine, si ha f (0) = g 0 (0) =
0. Analogamente, sapendo che Γ ha un massimo in x = k , si ricava f (k) = g 0 (k) = 0. Studiando la
derivata prima di g , si ha che f è positiva fra 0 e k e successivamente negativa decrescente. Quindi da
g 00 (h) = 0, si ha che x = h è un punto di massimo. Inoltre x = w è un punto di minimo all'estremo del
campo in cui si considera la funzione. Complessivamente il graco della funzione ha il seguente andamento.
2. Sarà g(x) = ax3 + bx2 + cx + d. Per le condizioni date, si ha d = 0 (g(0) = 0). Quindi:
g(x) = ax3 + bx2 + cx
g 0 (x) = 3ax2 + 2ax + c
.
Da g 0 (0) = 0 si ricava anche c = 0 e quindi, in denitiva:
g(x) = ax3 + bx2
g 0 (x) = 3ax2 + 2bx
g 00 (x) = 6ax + 2b
b
. Inoltre g 0 (x) = 0 quando
3a
2b
3ax2 + 2bx = 0, cioè per x = 0 e x = − . Da g(x) = 0 si ricava ax3 + bx2 = 0; quindi x = 0 oppure
3a
b
x = − = w.
a
Se per x = h si ha un punto di esso, allora g 00 (h) = 6ah + 2b = 0; quindi h = −
b
2
1
= 3 e g(1) = a + b = , si ricava a = − e b = 1. I punti di intersezione del graco di g con la
a
3
3
√ 2
2
2
retta y = sono i punti P (1, ) e Q(1 + 3, ). Le tangenti in questi punti hanno coecienti angolari,
3
3
3
√
rispettivamente, m = 1 e m = −2 (calcolando g 0 (1) e g 0 (1 + 3)). Dunque le normali in P e Q alla curva
√
2
2
1
hanno rispettivamente equazioni y − = −(x − 1) e y − = (x − 1 − 3).
3
3
2
3. Da −
4. Si può vedere il volume richiesto come somma di corone cilindriche di basi aventi raggi x e x+dx e altezza g(x),
dunque di volume 2πxg(x)dx. Complessivamente V =
corrispondente approssimativamente a 25, 43 litri.
1
R3
0
2πxg(x) dx = 2π
R3
0
1
81
(− x4 + x3 ) dx =
π dm3 ,
3
10
Problema 2 – ordinamento
√4
1. Da
√
√
si ha che gli unici punti stazionari sono
√2 è il punto di minimo assoluto e
Dal grafico si deduce subito che
punto di massimo assoluto con
√2.
2.
√2
2. L’origine è centro di simmetria in quanto
l’equazione tan
3. Per
0e
√2 è il
0
è funzione dispari. Risulta
2 ha come soluzione approssimata
2e
63°26′.
0, abbiamo:
4
e quindi il grafico della precedente figura nel primo quadrante.
Per simmetria, otteniamo il grafico complessivo (la curva data si poteva scrivere
come | |
| |√4
):
Data la simmetria della curva, si ha:
4
4. L’equazione
4
1 è soddisfatta per
4
3
4
32
3
2
(gli altri valori
0 non sono accettabili tenendo conto del codominio di
).
con
Risolvendo l’equazione per via grafica si ottengono due soluzioni (di tali
e
,
volendo, si possono anche trovare le espressioni analitiche:
8
,
si vede – servirà in seguito – che:
cos
Risulta
a)
b) cos
∙ ′
√64
4
√2
e quindi
4
;
).
0 quando:
0
0 ovvero, in questo caso,
.
√2; la condizione b) dà
La condizione a) dà
e
Essendo
√2
, si conclude subito che
0e
assoluto;
√2 è punto di minimo relativo (
e
.
2 sono punti di minimo
sono punti di massimo
assoluto).
Dal grafico si deduce immediatamente che l’equazione
soluzioni distinte per
∈ sin 2, 1 .
ha quattro
Questionario – Ordinamento
1. Dal teorema dei seni abbiamo:
sin
4
da cui sin
sin 30°
3
arcsin .
41,81 °. Gli
Con l’uso di una calcolatrice si ottiene il valore
equivalgono a
∙
di grado
primi sessagesimali (tra 48′ e 49′). Quindi
41°49′.
2. Per avere un poliedro regolare, in ogni vertice devono concorrere almeno tre
poligoni regolari. L’esagono regolare ha angoli al vertice di 120° quindi tre di essi
concorrenti in un vertice stanno su un piano.
3. Il generico termine dello sviluppo del binomio è dato da:
2
3
Il sistema:
3
2
4
9
ammette una soluzione n = 5 (e k = 2).
4. Il volume di Ω è:
∙
1
1
1
1
1
√
5. Occorre togliere dei 6000 numeri quelli che sono multipli di 2 oppure di 3
oppure di 5.
I multipli di 2 sono esattamente 3000.
I multipli di 3 sono esattamente 2000, ma di questi 1000 sono pari.
I multipli di 5 sono 1200, ma di questi 600 sono pari e 200 sono multipli di 3 non
pari.
In definitiva occorre togliere dai 6000:
3000+1000+400=4400 numeri
Ne rimangono 1600.
6. La lattina di superficie minima tra quelle a forma di parallelepipedo è il cubo.
Dunque, se è il suo lato, deve essere:
5 ∙ 10
10 ∙ √5
7. Il valor medio di
171mm
è:
1
9
da cui
4
9quindi
√36
8. Una funzione polinomiale di quarto grado che abbia due estremanti in x0 e –x0 con
e f(x0) = f(-x0) è simmetrica rispetto all’asse delle y. Abbiamo infatti:
4
3
4
2
3
0
2
0
Sottraendo le prime due equazioni e sommando la terza con la quarta otteniamo:
0
0
3
Poiché il determinante di questo sistema omogeneo è diverso da zero si ha: b=d=0. Cioè
la funzione è pari.
Nel nostro caso, la funzione data è simmetrica rispetto alla retta x=5/2; di conseguenza è
f(4) =f (1) = 0.
9. Deve essere
5
0, ovvero
5.
Deve inoltre essere:
3
log
5
log
5
5
3
8
3
0
In conclusione il dominio è dato da
10.
10
definita.
5, 3 .
26 è sempre positiva e la funzione al primo membro risulta sempre
Perché l’equazione data sia soddisfatta può essere l’esponente uguale a zero:
6
1
0
ovvero
3
2√2.
Può anche essere
10
26
5
10
21
0
ovvero
quindi:
7e
3.