RILIEVO DELLA CURVA DI RISONANZA DI
UN CIRCUITO LC PARALLELO
Se si fa variare la frequenza della f.e.m. che alimenta un
circuito LC parallelo, si trova che l’ ampiezza della corrente
raggiunge un minimo in corrispondenza del valore (frequenza di
risonanza):
0
1
2 LC
(1)
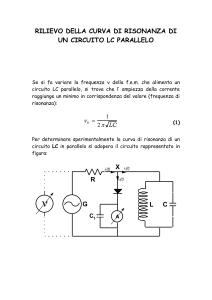
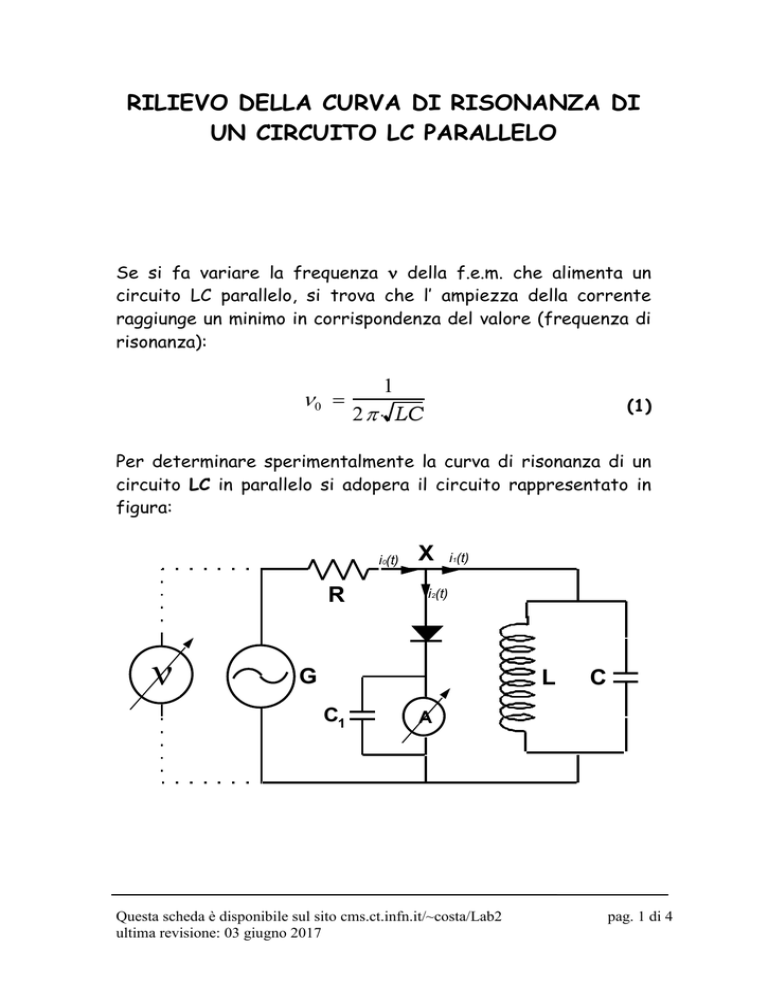
Per determinare sperimentalmente la curva di risonanza di un
circuito LC in parallelo si adopera il circuito rappresentato in
figura:
i0(t)
R
X
i1(t)
i2(t)
G
L
C1
C
A
Questa scheda è disponibile sul sito cms.ct.infn.it/~costa/Lab2
ultima revisione: 03 giugno 2017
pag. 1 di 4
Nel nodo X la corrente i0(t) si divide in i1(t), che passa
attraverso il circuito LC in oggetto, e i2(t) che attraversa l’
amperometro A. Tutte e 3 queste correnti variano nel tempo
con legge sinusoidale del tipo
in (t ) I n sen(2 t n )
e in ogni istante
(n 0,1,2)
i1(t) i2 (t) i0(t)
Tra le loro ampiezze sussiste inoltre sempre la relazione
I0 I1 I2
L’ uso di tale circuito relativamente complesso è reso
necessario dalle seguenti considerazioni:
La curva di risonanza va determinata adoperando un unico
strumento misuratore di corrente (o un’ unica scala in un
amperometro a diverse portate), altrimenti la corrente
varierebbe non solo al variare della frequenza, ma anche al
momento di cambiare strumento (o portata) in quanto cambia la
resistenza interna dello strumento e quindi l’ impedenza dell’
intero circuito.
Nella regione di frequenze attorno alla risonanza l’ ampiezza
della corrente raggiunge i valori più piccoli, che sarebbero
misurati presumibilmente nella porzione inferiore della scala
dello strumento, dove l’ errore relativo che si commette è
maggiore.
Pertanto non conviene misurare direttamente l’ ampiezza I1
della corrente i1(t) ma quella, I2, della corrente i2(t). Infatti, se
Questa scheda è disponibile sul sito cms.ct.infn.it/~costa/Lab2
ultima revisione: 03 giugno 2017
pag. 2 di 4
si ha l’ accortezza di fare in modo che l’ ampiezza della
corrente i0(t), I0, non vari al variare della frequenza, allora I0 è
una costante e
I2=I0-I1 varierà con la frequenza con
andamento esattamente inverso a I1. I2 presenterà quindi una
curva di risonanza con un massimo per =0, come in un circuito
RLC serie. Sebbene ribaltata, la curva rilevata misurando I2
avrà la stessa forma di I1 e presenterà il suo massimo in
corrispondenza dello stesso valore di per il quale I1 avrebbe
presentato il suo minimo.
Il diodo posto nel ramo dove scorre i2(t) ha la funzione di
raddrizzare la corrente che attraversa l’ amperometro. Infatti
non è possibile adoperare un normale amperometro per correnti
alternate, in quanto tale tipo di apparecchio è appropriato per
correnti di frequenze prossime a quella della rete elettrica (50
Hz), mentre nell’ esperienza si raggiungono frequenze dell’
ordine dei kHz e oltre. Il punto è che la corrente continua
misurata dall’ amperometro in queste condizioni è esattamente
proporzionale all’ ampiezza della corrente alternata da misurare
in quel ramo, I2. Il condensatore C1 in parallelo all’ amperometro
costituisce, insieme alla resistenza interna dell’ amperometro
rA un circuito RC, il quale in regime sinusoidale, si comporta, ai
capi di rA come un circuito passa-alto, e ai capi di C1 come un
filtro passa-basso. Ciò assicura che la corrente scorre
essenzialmente attraverso l’ amperometro solo se la sua
frequenza è alta e l’ ago come desiderato non può seguirne la
variazione di ampiezza, mentre quando la frequenza fosse molto
bassa, la corrente sarebbe assorbita essenzialmente dal
condensatore causandone la carica.
Questa scheda è disponibile sul sito cms.ct.infn.it/~costa/Lab2
ultima revisione: 03 giugno 2017
pag. 3 di 4
Modo di operare
1. Realizzare il circuito di figura, utilizzando, se disponibile,
anche un frequenzimetro. NOTA: La frequenza può essere
letta sul generatore (direttamente sul display digitale se il
generatore ne è fornito, oppure moltiplicando il valore
indicato sul pulsante selettore dell’ intervallo di frequenze
il fattore moltiplicativo sulla manopola in modelli più vecchi),
ma, se disponibile, il frequenzimetro fornisce una misura
molto più precisa. Il frequenzimetro si collega in parallelo
come un voltmetro.
2. Variare la frequenza della tensione fornita dal generatore e
rilevare in corrispondenza l’ ampiezza della corrente
misurata dall’ amperometro. Accertarsi che l’ intervallo di
frequenze esplorate comprenda il valore di risonanza, cioè
che al crescere della frequenza la corrente cresca e poi,
raggiunto un massimo, decresca. NOTA: Per ogni frequenza,
prima di leggere la corrente occorre ripristinare l’ ampiezza
della tensione fornita dal generatore su un valore prefissato
(p.es. 3 Volt), mediante l’ apposita manopola. Questo è
necessario affinchè l’ ampiezza I0 della corrente i0(t) sia
costante come ipotizzato sopra. L’ ampiezza della tensione
fornita dal generatore tende a variare perchè con la
frequenza varia l’ ampiezza della corrente e quindi la caduta
di tensione nella resistenza interna del generatore.
3. Tracciare la curva di risonanza, I2 in funzione di ;
individuare il valore della frequenza di risonanza 0 e, nota o
misurata la capacità del condensatore C, dedurre il
coefficiente di autoinduzione L della bobina dalla (1).
Questa scheda è disponibile sul sito cms.ct.infn.it/~costa/Lab2
ultima revisione: 03 giugno 2017
pag. 4 di 4