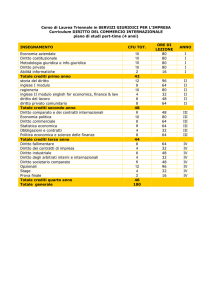
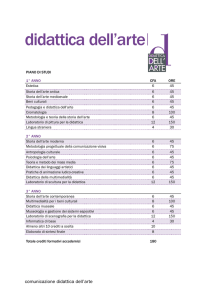
I ANNO - I SEMESTRE
Calcolo 1 - 7 crediti (Prof. A. Porretta)
Numeri reali e complessi. Funzioni. Limiti. Successioni e serie. Funzioni continue. Derivata, retta
tangente. Massimi, minimi, studio di funzioni. Regola di De l'Hopital. Polinomio di Taylor e
applicazioni. Integrale di Riemann, teorema fondamentale del Calcolo. Metodi di integrazione. Integrali
impropri.
TESTI CONSIGLIATI !E. Giusti (Analisi Matematica 1,Bollati Boringhieri)!E. Giusti (Esercizi e
complementi di analisi matematica 1,Bollati Boringhieri,) !B. Demidovich (Esercizi e problemi di Analisi
Matematica,Ed. Riuniti)
Calcolo 1 - 7 crediti (Corso in vigore fino all'a.a. 2002-2003)!Calcolo differenziale e integrale
per le funzioni di una variabile. Calcolo combinatorio, numeri complessi, funzioni elementari in campo
complesso. L'oscillatore armonico smorzato
Calcolo 2 - 5 crediti (Prof. F. Fidaleo - richiede il superamento di Calcolo 1)
FUNZIONI DI DUE VARIABILI. Grafici, curve di livello, continuità e limiti. Insiemi di punti del piano:
frontiera, insiemi aperti, chiusi, limitati e connessi: teoremi relativi. Derivate parziali, gradiente,
differenziale, teorema delle funzioni implicite, massimi e minimi liberi e vincolati. Derivate seconde e
successive. Integrali curvilinei, forme differenziali e loro integrazione. !FUNZIONI DI TRE E PIU'
VARIABILI. Estensioni del caso bidimensionale; campi vettoriali.
TESTI CONSIGLIATI !E. Giusti: Analisi Matematica, voll I e II; Bollati Boringhieri, Torino F! . Conti:
Calcolo, teoria e applicazioni, McGraw-Hill !A. Schiaffino, A. Vignoli: Introduzione all'Analisi
Matematica, vol. II; Aracne, Roma !B. Demidovic: Esercizi e problemi di Analisi Matematica; Editori
Riuniti, Roma
Calcolo 2 - 7 crediti (Corso in vigore fino all'a.a. 2002-2003)!Calcolo differenziale nel piano e
nello spazio. Integrazione di forme differenziali (grado 1). Formula di Taylor. Successioni e serie.
Geometria 1 - 7 crediti (Prof. M. Letizia)
Geometria del piano e dello spazio, vettori geometrici rette e piani, equazioni parametriche e
cartesiane, prodotto scalare e vettoriale, generalizzazione allo spazio R^n, sottospazi vettoriali ed
affini di R^n. Sistemi di riferimento. Matrici e determinanti. Risoluzione dei sistemi lineari eliminazione
di Gauss Rango di una matrice e numero dei parametri liberi dello spazio delle soluzioni di un sistema
lineare. Coniche e quadriche in forma canonica Esempi di curve e superfici, equazioni parametriche e
cartesiane.
TESTI CONSIGLIATI !S.Abeasis: Elementi di Algebra Lineare e Geometria; Ed. Zanichelli !M. Abate:
Geometria; Ed. McGraw-Hill
Geometria 1 - 5 crediti (Corso in vigore fino all'a.a. 2002-2003)!Esempi di spazi vettoriali
geometrici e numerici. Geometria analitica nel piano e nello spazio. !Coniche e Quadriche in forma canonica.
Esempi di curve e superfici: equazioni parametriche e cartesiane.
Meccanica 1 - 6 crediti (Prof. P. Chiaradia)
Cinematica e Dinamica del punto materiale (forze, lavoro ed energia, momento angolare, leggi di
conservazione). Moti relativi. Dinamica dei sistemi di punti materali. Urti. Dinamica del corpo rigido.
Cenni di statica
Matematica 0 - 0 crediti (corso di recupero per studenti con debiti formativi)
Operazioni sui numeri reali. Trigonometria. Equazioni algebriche. Disequazioni.
Corso di lingua inglese - 4 crediti (Prof. F. Fantera)
Main Objectives: The course aims at the consolidation and improvement of the four language skills
(reading, writing, listening, and speaking) through a wide range of activities in the field of science.
Course content: The lessons will be organized around various thematic units based on the course
textbook and articles taken from authentic sources such as newspapers, the internet, specialized
journals and hand-outs distributed in class. Each unit will focus on enhancing general language
structures, vocabulary and functions on the basis of the readings and in class discussions. Particular
attention will be given to improving reading comprehension and summarizing skills.
I ANNO - II SEMESTRE
Geometria 2 - 7 crediti (Prof. S. Trapani - richiede il superamento di Geometria 1)
Spazi vettoriali, sottospazi. Somme dirette. Teorema di Grassmann. Applicazioni lineari, matrici
associate, cambiamenti di base. Autovalori, autovettori, diagonalizzazione. Prodotti scalari,
disuguaglianza di Schwartz. Basi ortonormalizzazione di Graham-Smith. Matrici associate ad un
prodotto scalare rispetto ad una base. Aggiunto di un operatore, operatori simmetrici, operatori
hermitiani, diagonalizzazione di operatori, teorema spettrale. Matrici ortogonali ed unitarie. Forma
canonica metrica delle iperquadriche.
TESTI CONSIGLIATI !Lang, Algebra lineare, Boringhieri; Silvana Abeasis, Elementi di algebra lineare e
geometria, Zanichelli.
Geometria 2 - 7 crediti (Corso in vigore fino all'a.a. 2002-2003)!Matrici e determinanti.
Sistemi di equazioni lineari ed eliminazione di Gauss. !Spazi vettoriali di dimensione finita. Operatori lineari;
endomorfismi e diagonalizzazione. Spazi vettoriali metrici. Operatori hermitiani ed unitari. Applicazioni allo
studio delle coniche e quadriche.
Laboratorio 1 - 8 crediti (Prof.ssa R. Bernabei)
Grandezze fisiche. Strumenti di misura e loro caratteristiche. Errori di misura e loro propagazione.
Misure di grandezze meccaniche e termiche connesse alle esperienze di laboratorio. Trattamento
statistico dei risultati di una misura. Distribuzioni limite. Metodo dei minimi quadrati: regressione
lineare. Esercitazioni di laboratorio.
Laboratorio di Informatica 1 - 4 crediti (Docente da definire)
Cenni sull’architettura di Computer: Introduzione, mod. Von Neumann, modello a Bus, Circuiti
integrati, Livelli di astrazione di un Calcolatore - Memorie: memorie multilivello, memorie cache,
prestazioni delle CPU - Misura delle prestazioni di una CPU (Clock speed, CPI, flops, etc.),
architetture CISC e RISC, cenni sul Codice Macchina, generazione di numeri casuali Rappresentazione in memoria dei numeri: formati intero e virgola mobile, rapprentazione in
complemento a due, addizione, sottrazione e moltiplicazione; Diagrammi di flusso, Programmazione
Strutturata, Progettazione Bottom-Up e Top-Down - Codici ASCII e Unicode, files binari e files
formattati - Memorie secondarie, dischi magnetici e ottici -Comunicazione tra calcolatori: connessioni
seriali, reti, links fisici, protocolli di comunicazione, servizi - Lo Scilab con esercitazioni volte a
risolvere problemi di fisica.
Meccanica 2 - 6 crediti (Prof. P. Chiaradia)
Gravitazione universale. Massa inerziale e gravitazionale. Campo ed energia potenziale gravitazionali.
Leggi di Keplero. Proprietà statiche e dinamiche dei fluidi. Legge di Stevino. Viscosità e fluido ideale.
Teorema di Bernoulli e applicazioni. Oscillazioni e onde. Oscillatore armonico. Oscillazioni forzate e
risonanza Equazione delle onde piane. Onde in una corda tesa.
Termodinamica - 5 crediti (Prof. P. Chiaradia-richiede il superamento di Meccan. 2)
Temperatura e termometri. Principio zero. Calore. Primo Principio. Energia interna. Calori specifici.
Cambiamenti di fase. Trasmissione del calore. Gas ideali (Leggi, Equazione di stato, Trasformazioni
cicliche) e Gas reali (Equazione di Van der Waals). Teoria cinetica dei gas. Secondo principio.
Teorema di Carnot. Temperatura termodinamica assoluta. Terorema di Clausius. Entropia. Terzo
principio della termodinamica (cenni). Potenziali termodinamici (cenni).
II ANNO - I SEMESTRE !
Calcolo 3 - 9 crediti (Prof. A. Schiaffino - richiede il superamento di Calcolo 2)
Integrali multipli: concetti generali, teorema della divergenza e del rotore. Equazioni differenziali caso
lineare, esponenziale di una matrice. Caso non lineare, integrali primi e loro uso nella ricerca delle
soluzioni. Serie e integrale di Fourier. Trasformata di Laplace
TESTI CONSIGLIATI !M. Bramanti, C.D. Pagani, S. Salsa Matematica (seconda edizione) Zanichelli,
Bologna !E. Giusti: Analisi Matematica, vol. II; Bollati Boringhieri, Torino !V. Smirnov: Matematiche
Superiori, voll I e II; Editori Riuniti, Roma !N. Piskunov: Calcolo differenziale e integrale; Editori Riuniti,
Roma !B. Demidovic: Esercizi e problemi di Analisi Matematica; Editori Riuniti, Roma !
Calcolo 3 - 6 crediti (Corso in vigore fino all'a.a. 2002-2003)!Calcolo integrale nel piano e nello
spazio. Calcolo differenziale in dimensione finita. Equazioni differenziali ordinarie.
Chimica - 7 crediti (Prof.ssa M.L. Terranova)
Struttura della Tavola Periodica. Elementi e composti. Proprietà generali degli elementi dei gruppi
rappresentativi. Formule ed equazioni chimiche. Il legame chimico. Calore e lavoro nei sistemi chimici.
Lo stato di equilibrio: il potenziale chimico, la costante di equilibrio. Equilibrio e reversibilità in
processi chimici e trasformazioni di fase. Le soluzioni. Acidi, basi e sali. Dissociazione ionica e
trasporto di cariche. Le proprietà colligative. Equilibri omogenei ed eterogenei in soluzione acquosa.
Reazioni redox. Celle elettrochimiche. Potenziali elettrodici e forza elettromotrice di una cella.
Elettrolisi. Cenni di cinetica chimica. Cenni di chimica organica.
Elettromagnetismo 1 - 6 crediti (Prof. R. Santonico)
La legge di Coulomb e il campo elettrico. La legge di Gauss. Il potenziale elettrico. Capacità.
Dielettrici. Corrente e resistenza. Circuiti elettrici. Campo magnetico costante nel vuoto. 8 Legge di
Ampère.
Laboratorio Calcolo - 6 crediti (Dott. G. De Gasperis)
Elementi di programmazione e loro applicazione nella soluzione di problemi numerici. Grafica di
funzioni in 1 e 2 dimensioni. Analisi multivariata.
!Fluidodinamica - 6 crediti (Dott. F. Toschi)
Equazioni di un fluido non viscoso e principali leggi di conservazione. Fluidi in due dimensioni. Effetto
della viscosità di un fluido. Stabilità dei moti fluidi stazionari: strato limite e sistemi di Rayleigh Benard.
Transizione alla turbolenza e boundary layer turbolento.
II ANNO - II SEMESTRE
Elettromagnetismo 2 - 6 crediti (Prof. R. Santonico)
Campo magnetico costante nella materia. Induzione elettromagnetica. Autoinduzione e induzione
mutua. Correnti alternate. Oscillazioni elettriche. Equazioni di Maxwell. Onde elettromagnetiche.
Relatività Speciale e Invarianza relativistica delle equazioni di Maxwell.
Ottica - 3 crediti (Prof. R. Santonico)
Riflessione e rifrazione. Ottica geometrica (specchi, lenti e strumenti ottici). Interferenza. Diffrazione.
Elementi di ottica dei corpi anisotropi.
Meccanica analitica - 6 crediti (Prof. L. Triolo -richiede il superamento di Calcolo
3 e Meccanica 1)
Equazioni di Lagrange. Formulazione variazionale. Simmetrie e costanti del moto. Equazioni di
Hamilton. Integrabilità, trasformazioni canoniche, equazione di Hamilton Jacobi.
TESTI CONSIGLIATI !Esposito, Appunti di Meccanica Razionale!Appunti del Docente
Meccanica analitica - 4 crediti (Corso in vigore fino all'a.a. 2002-2003, con lo stesso
programma)
Meteorologia dinamica - 7 crediti (Prof. R. Benzi richiede il superamento di
Elettromagnetismo 2)
Termodinamica dell'Atmosfera. Bilancio geostrofico ed equazione del vento termico. Equazioni
primitive. Onde di gravità nell'atmosfera. Approssimazione quasi geostrofica. Circolazione simmetrica
e circolazione di Hadley. Instabilità baroclina. Onde stazionarie e effetti orografici. La variabilità a
bassa frequenza. Il concetto di predicibilità.
Corso a scelta - 6 crediti
III ANNO - I SEMESTRE
Climatologia - 7 crediti (Dott. F. Fierli)
Bilancio radiativo della terra. Tempi caratteristici del sistema climatico e ruolo della circolazione
oceanica. Glaciazioni e interglaciazioni. Variazioni interannuali. Il fenomeno del El Nino. Effetti
antropogenici sul clima. Metodi di misura delle variazioni climatiche. Modelli di simulazione del clima.
Fisica Atmosfera - 6 crediti (Dott. F. Travaglioni)
Costituzione fisica dell'atmosfera e principali cambiamenti di stato. Lo strato limite superficiale e il
bilancio energetico. Effetti radiativi nell'atmosfera. Corpi nuvolosi e convezione atmosferica.
Metodi Matematici della Fisica 1 - 6 crediti (Prof. G. Rossi - richiede il
superamento di Calcolo 3, Geometria 2)
Funzioni analitiche di variabile complessa. Teoremi di Cauchy. Funzioni monodrome e polidrome.
Spazi vettoriali ad un numero finito di dimensioni: vettori e operatori lineari. Autovalori e autovettori.
Rappresentazione spettrale. Spazio di Hilbert e cenni di analisi funzionale. Polinomi ortogonali.
Operatore aggiunto, autoaggiunto, unitario e normale. Cenni di teoria delle distribuzioni. Serie e
trasformate di Fourier. Trasformata di Laplace. Funzioni analitiche di variabile complessa. Teoremi di
Cauchy. Funzioni monodrome e polidrome. Spazi vettoriali ad un numero finito di dimensioni: vettori
e operatori lineari. Autovalori e autovettori. Rappresentazione spettrale. Spazio di Hilbert e cenni di
analisi funzionale. Polinomi ortogonali. Operatore aggiunto, autoaggiunto, unitario e normale. Cenni
di teoria delle distribuzioni. Serie e trasformate di Fourier. Trasformata di Laplace.
Metodi Matematici della Fisica 1 - 7 crediti (Corso in vigore fino all'a.a. 2002-2003,
con lo stesso programma)
Meccanica Quantistica - 6 crediti (Prof. M. Bianchi (richiede il superamento di
Calcolo 3, Geometria 2, Meccanica 2, Elettromagnetismo 2 e Meccanica Analitica)
Crisi della Fisica Classica. Corpo nero. Effetto fotoelettrico. Fenomeni ondulatori, interferenza e
diffrazione. Postulati della Meccanica Quantistica. Equazione di Schroedinger unidimensionale: buca di
potenziale, effetto tunnel, oscillatore armonico. Equazione di Schroedinger tridimensionale: atomo di
idrogeno. Momento angolare, composizione dei momenti angolari. Spin e momento magnetico.
Particelle identiche, principio di Pauli. Teoria delle perturbazioni indipendenti dal tempo, teoria delle
perturbazioni dipendenti dal tempo. Metodi variazionali.
Corso a scelta - 6 crediti
III ANNO - II SEMESTRE
Laboratori Metodi Computazionali 1 - 6 crediti (Dr. V. Malvestuto)
Metodi di derivazione e integrazione numerica. Integrazione di equazioni differenziali e analisi della
soluzione. Spettro di potenza e funzioni di correlazione di segnali numerici.
Laboratorio Fisica Atmosfera - 6 crediti (Dott.ssa S. Argentini)
Metodi di misura dello strato limite planetario: stazioni meteo, anemometro sonico, sodar, wind
profiler. Misure del bilancio energetico dello strato limite. Analisi dati: bilancio superfi ciale, bilancio
radiativo, parametrizzazione dei flussi turbolenti, circolazione.
Fisica Moderna - 6 crediti (Prof. M. De Crescenzi - richiede il superamento di
Meccanica Quantistica 1)
Il corso è diretto a studenti del terzo anno che intendono acquisire una preparazione di base sui
fondamenti sperimentali e teorici della struttura degli atomi e dei solidi. Particolare riguardo sarà dato
alle applicazioni di nuovi fenomeni fisici quali le nanostrutture, la superconduttività ad alta
temperatura, l'STM (scanning tunneling microscopy) e il laser a semiconduttore.
TESTI CONSIGLIATI: !R. Eisberg e R. Reisnick: "Quantum Physics" per atomi e introduzione storica,
!S.M.Sze: "Fisica dei dispositivi a semiconduttore",!C. Kittel "Introduzione alla Fisica dello Stato Solido".
Tirocinio - 5 crediti
Prova finale - 5 crediti