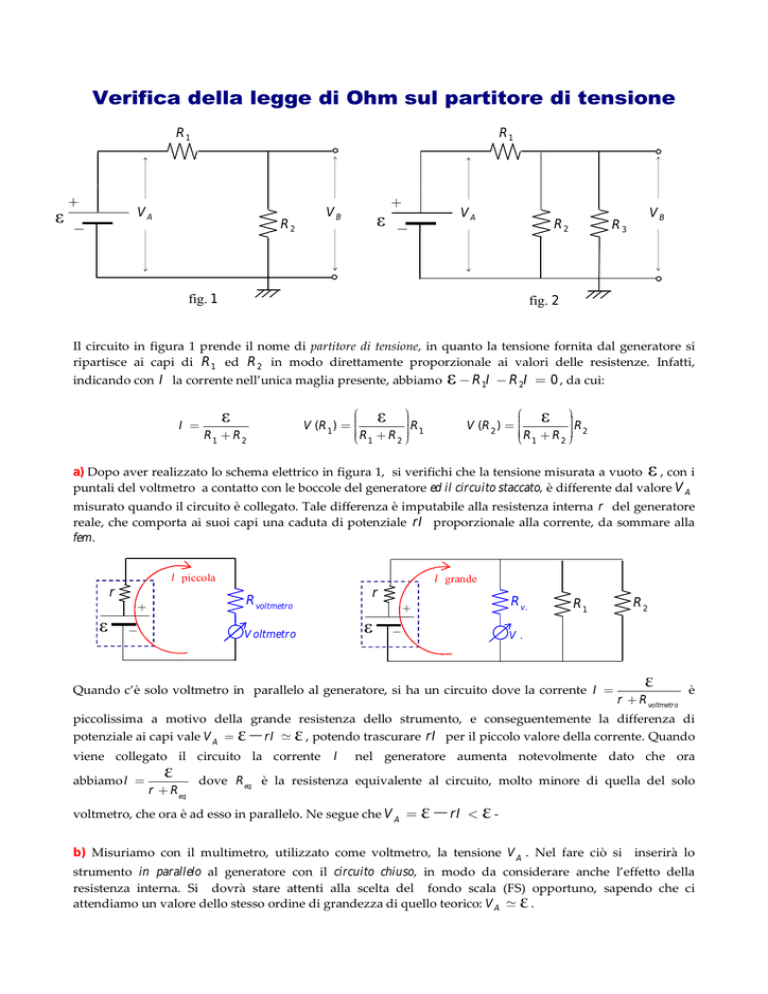
Verifica della legge di Ohm sul partitore di tensione
R1
ε
R1
VA
R2
VB
ε
VA
R2
fig. 1
VB
R3
fig. 2
Il circuito in figura 1 prende il nome di partitore di tensione, in quanto la tensione fornita dal generatore si
ripartisce ai capi di R1 ed R2 in modo direttamente proporzionale ai valori delle resistenze. Infatti,
indicando con I la corrente nell’unica maglia presente, abbiamo
I
ε
R1 R2
ε
R
V (R1 )
R1 R2 1
ε R1I R2I 0 , da cui:
ε
R
V (R2 )
R1 R2 2
ε
a) Dopo aver realizzato lo schema elettrico in figura 1, si verifichi che la tensione misurata a vuoto , con i
puntali del voltmetro a contatto con le boccole del generatore ed il circuito staccato, è differente dal valore VA
misurato quando il circuito è collegato. Tale differenza è imputabile alla resistenza interna r del generatore
reale, che comporta ai suoi capi una caduta di potenziale rI proporzionale alla corrente, da sommare alla
fem.
I piccola
r
Rvoltmetro
ε
I grande
Voltmetro
r
Rv .
ε
R1
R2
V.
Quando c’è solo voltmetro in parallelo al generatore, si ha un circuito dove la corrente I
ε
r Rvoltmetro
è
piccolissima a motivo della grande resistenza dello strumento, e conseguentemente la differenza di
potenziale ai capi vale VA ε rI ε , potendo trascurare rI per il piccolo valore della corrente. Quando
viene collegato il circuito la corrente I
abbiamo I
ε
r Req
nel generatore aumenta notevolmente dato che ora
dove Req è la resistenza equivalente al circuito, molto minore di quella del solo
voltmetro, che ora è ad esso in parallelo. Ne segue che VA
ε rI ε -
b) Misuriamo con il multimetro, utilizzato come voltmetro, la tensione VA . Nel fare ciò si inserirà lo
strumento in parallelo al generatore con il circuito chiuso, in modo da considerare anche l’effetto della
resistenza interna. Si dovrà stare attenti alla scelta del fondo scala (FS) opportuno, sapendo che ci
attendiamo un valore dello stesso ordine di grandezza di quello teorico: VA ε .
Si misura VB sempre con lo stesso multimetro, ponendolo stavolta in parallelo ad R2 , e se occorre
abbassando il valore di FS (basandosi sul valore atteso in teoria: VB
R2
R1 R2
VA ).
c) Dopo aver calcolato il valore teorico per la corrente, scegliamo il FS giusto sullo strumento in (base alla
VA
teoria I
) ed eseguiamo la misura di I utilizzando il multimetro come amperometro. Bisognerà
R1 R2
quindi interrompere in un punto il circuito e chiuderlo inserendo lo strumento in serie ad R1 ed R2 .
d) Si ripetono i passi a-b-c per tre-quattro valori differenti di tensione, girando la manopola del generatore,
ed eseguendo i calcoli teorici in anticipo, in modo da scegliere il giusto fondo scala per ciascuna misura. Si
completi in questo modo la tabella corrispondente ai valori scelti per R1 ed R2 . L’esperienza viene replicata
utilizzando poi valori R1 R2 ed R1 R2 , compilando le relative tabelle.
e) Le misure così trovate vanno riportate su di un grafico con la tensione d’ingresso, VA , sulle ascisse e
quella di uscita, VB , sulle ordinate. La relazione che le lega:
R
2
V
VB
R1 R2 A
VB
R2 R1
(VB VA )
nel piano VA , VB è rappresentata da una retta passante per
l’origine, detta transcaratterisitica del circuito. Il suo
coefficiente angolare dipende dalla relazione che sussiste fra i
valori di R1 ed R2 . La retta coincide con l’asse VB 0 se
R2 R1
(VB
R2 0 , e la sua pendenza aumenta gradualmente al
1
V )
2 A
V
A
R2 0
1
2
nel limite R2 R1 , approssimandosi alla bisettrice VB VA . Per ciascuna delle coppie di valori scelti per le
crescere di R2 , diventando VB VA quando R1 R2 , e,
resistenze si dovrà allora visualizzare sul grafico la retta teorica e, riportando i punti sperimentali delle varie
tabelle, osservare l’accordo dei dati con la teoria. Si faccia attenzione che, a seconda della resistenza R2 , il
valore di VB passa da qualche Volt a qualche centesimo di Volt, e quindi sarà necessario sovrapporre
differenti unità di misura sull’ asse delle ascisse, oppure fare due grafici separati.
f) Si realizzi poi il circuito in fig. 2 dove ora la tensione VB viene presa ai capi del parallelo
R2 //R3
R2R3
R2 R3
, il cui valore ha la proprietà di essere inferiore a quello della più piccola fra le due
resistenze. In questo caso R1 è in serie al parallelo R2 //R3 , e quindi abbiamo:
I
VA
R1
R2 R3
R2 R3
VB IR//
VA
RR
R1 2 3
R2 R3
R R
2 3
R R
2
3
La coppia R2 //R3 è un partitore di corrente: la I che entra nel nodo ai capi del parallelo si ripartisce in I 2 ed
I 3 , inversamente proporzionali alle resistenze. Con queste formule, utilizzando per R3 i valori suggeriti
nella scheda, si calcoli di nuovo il FS da usare per le misure di tensione e di corrente. Si ripetano i passi,
misurando VB , I , e facendo il grafico della transcaratteristica. Si quindi traggano le opportune conclusioni
sul comportamento rivelato quando R3 è più piccola, confrontabile oppure più grande di R2 .
Il codice a colori
Valore
Nero 0
Marrone 1
Rosso 2
Arancio 3
Giallo 4
Verde 5
Blu 6
Viola 7
Grigio 8
Bianco 9
Moltiplicatore
Argento
0,01
Oro
0,1
Nero
Marrone
Rosso
Arancio
Giallo
Verde
Blu
Viola
1
10
100
1K
10K
100K
1M
10M












