Una funzione è una “legge” che associa ad elementi di un insieme elementi di un altro
insieme.
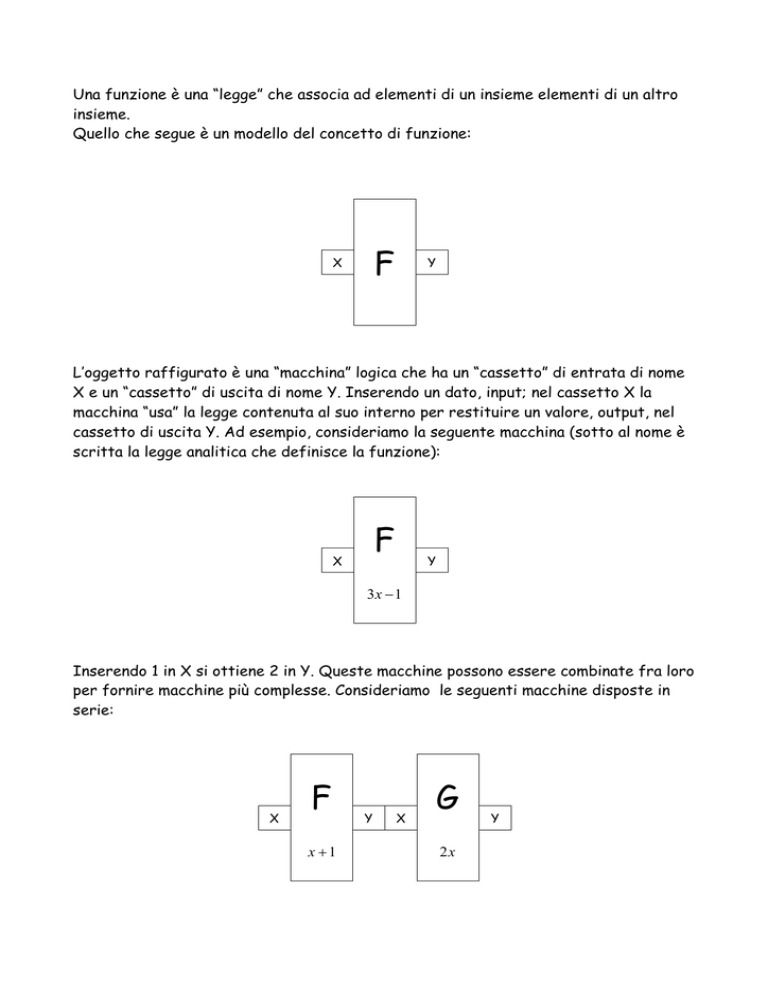
Quello che segue è un modello del concetto di funzione:
F
X
Y
L’oggetto raffigurato è una “macchina” logica che ha un “cassetto” di entrata di nome
X e un “cassetto” di uscita di nome Y. Inserendo un dato, input; nel cassetto X la
macchina “usa” la legge contenuta al suo interno per restituire un valore, output, nel
cassetto di uscita Y. Ad esempio, consideriamo la seguente macchina (sotto al nome è
scritta la legge analitica che definisce la funzione):
F
X
Y
3x − 1
Inserendo 1 in X si ottiene 2 in Y. Queste macchine possono essere combinate fra loro
per fornire macchine più complesse. Consideriamo le seguenti macchine disposte in
serie:
X
F
x +1
Y
X
G
2x
Y
Cosa si ottiene stavolta inserendo 1? Se invertiamo l’ordine delle macchine elementari
otteniamo la stessa macchina complessa precedente? In quali casi questo succede?
Talvolta una macchina ha una sua inversa, cioè una macchina che posta in sequenza con
essa produce come macchina complessa la funzione Identità. La funzione identità è la
funzione per la quale l’output coincide con l’input. Quando è possibile costruire la
macchina inversa? Data una macchina complessa come è possibile costruire, se esiste,
la sua inversa?
Consideriamo l’equazione 3x-1=0. Il problema posto dall’equazione “qual è il valore che
sostituito alla x verifica l’uguaglianza” è equivalente al seguente problema:
qual è l’input della macchina * che fornisce 0 come output? Questo problema può
essere risolto costruendo la macchina inversa di *. La soluzione è l’output che fornisce
questa macchina quando ha come input 0.
X
F
Y
3x − 1
X
F
3x
Y
X
G
⇒
Y
X
G’
x −1
x +1
0→
X
F’
x +1
3
Y
→
−1
3
Y
X
F’
x
3
Y
L’uso di questo modello è utile in quanto rende intuitiva la comprensione di concetti
come quello di variabile, incognita, funzione, funzione composta, funzione inversa e il
teorema: l’inversa di una funzione composta è la composizione delle funzioni inverse
elementari in ordine inverso. Inoltre permette di comprendere che un stesso concetto
può essere “visto” in modi diversi.










