UNIVERSITA` DEGLI STUDI DI TORINO FACOLTA` DI SCIENZE

UNIVERSITA’ DEGLI STUDI DI
TORINO
FACOLTA’ DI SCIENZE M.F.N.
Corso di Laurea in Fisica
Laboratorio di Fisica V
Anno Accademico 2004-2005
Mina Fabrizio
Pedrazzo Francesco
Ugliano Marcella
ii
Indice
1 Effetto Hall nei semiconduttori
1.1 Introduzione e fisica dell’esperienza . . . . . . . . .
1.1.1 Semiconduttori . . . . . . . . . . . . . . . .
1.1.2 Drogaggi P e N . . . . . . . . . . . . . . . .
1.1.3 Effetto Hall nei semiconduttori . . . . . . .
1.1.4 Termocoppia . . . . . . . . . . . . . . . . .
1.2 Caratterizzazione del campo magnetico . . . . . .
1.2.1 Setup sperimentale . . . . . . . . . . . . . .
1.2.2 Acquisizione dati . . . . . . . . . . . . . . .
1.2.3 Risultati . . . . . . . . . . . . . . . . . . . .
1.3 Misura del ciclo di isteresi magnetica del traferro .
1.3.1 Setup sperimentale . . . . . . . . . . . . . .
1.3.2 Acquisizione dati . . . . . . . . . . . . . . .
1.3.3 Risultati . . . . . . . . . . . . . . . . . . . .
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
1.4.1 Setup sperimentale . . . . . . . . . . . . . .
1.4.2 Acquisizione dati . . . . . . . . . . . . . . .
1.4.3 Risultati . . . . . . . . . . . . . . . . . . . .
1.5 Misura dell’effetto Hall - semiconduttore di tipo P
1.5.1 Setup sperimentale . . . . . . . . . . . . . .
1.5.2 Acquisizione dati . . . . . . . . . . . . . . .
1.5.3 Risultati . . . . . . . . . . . . . . . . . . . .
1.6 Misura della resistività di un semiconduttore . . .
1.6.1 Setup sperimentale . . . . . . . . . . . . . .
1.6.2 Acquisizione dati . . . . . . . . . . . . . . .
1.6.3 Risultati . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
1
3
4
7
10
10
12
13
15
15
16
16
21
21
23
25
35
35
35
35
43
44
46
47
2 Rivelazione di raggi cosmici
2.1 Introduzione e fisica dell’esperienza . . . . . . . . . .
2.1.1 Raggi cosmici . . . . . . . . . . . . . . . . . .
2.1.2 Scintillatori . . . . . . . . . . . . . . . . . . .
2.1.3 Fotomoltiplicatori . . . . . . . . . . . . . . .
2.1.4 Logica NIM . . . . . . . . . . . . . . . . . . .
2.2 Osservazione del rumore di fondo . . . . . . . . . . .
2.3 Determinazione della tensione di lavoro dei fototubi
2.3.1 Elaborazione dati . . . . . . . . . . . . . . . .
2.4 Misura della curva di coincidenza . . . . . . . . . . .
2.4.1 Acquisizione dati . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
55
55
55
58
64
69
72
75
78
81
83
iii
iv
INDICE
2.5
2.6
2.4.2 Risultati . . . . . . . . . . . .
Misura di eventi accidentali . . . . .
2.5.1 Setup sperimentale . . . . . .
2.5.2 Acquisizione dati . . . . . . .
2.5.3 Risultati . . . . . . . . . . . .
Misura dell’efficienza di un rivelatore
2.6.1 Setup sperimentale . . . . . .
2.6.2 Acquisizione dati . . . . . . .
2.6.3 Risultati . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
83
86
86
86
87
89
90
91
91
Capitolo 1
Studio della resistenza di
un semiconduttore in
funzione della temperatura
e misura dell’effetto Hall
nei semiconduttori
1.1
Introduzione e fisica dell’esperienza
Lo scopo dell’esperienza è la determinazione delle caratteristiche di conduzione
dei semiconduttori, attraverso la misura di alcuni parametri fisici macroscopici
e microscopici. Utilizzando un campione di materiale semiconduttore dapprima
si studierà il variare della resistenza elettrica in funzione della temperatura,
quindi si sfrutterà l’effetto Hall per determinare la concentrazione dei portatori
di carica.
1.1.1
Semiconduttori
Analizzando il moto dei portatori di carica in un materiale i cui capi sono sottoposti ad una determinata differenza di potenziale si può osservare che essi non
procedono, come si potrebbe prevedere in base alla teoria classica, secondo traiettorie rettilinee parallele alle linee del campo elettrico generato dalla tensione
applicata: il moto è influenzato dalla presenza di atomi o ioni contro i quali i
portatori urtano.
In assenza di campo elettrico, si può definire il libero cammino medio l ed il
tempo medio tra un urto e il successivo τ , legati dalla relazione
τ=
l
v
dove v è la velocità media dei portatori di carica nel materiale considerato.
1
2
Effetto Hall nei semiconduttori
Applicando una differenza di potenziale ai capi del materiale in esame si
può pensare che le traiettorie rettilinee percorse dai portatori di carica, tra un
urto e il successivo, vengano deflesse dalle linee del campo elettrico che fornisce
al singolo portatore un’accelerazione pari al rapporto tra la forza di Coulomb
corrispondente e la massa dello stesso.
→
−
eE
→
−
a =
m
La velocità acquisita da un portatore di carica dopo l’i-esimo urto diventa
quindi pari a
→
−
eE
→
−
−
τ
v i+1 = →
vi−
m
−
Il valor medio delle velocità →
v i è pari a zero, essendo la distribuzione delle
velocità in seguito agli urti successivi casuale: si può quindi definire dopo una
serie di N urti una velocità di deriva media, proporzionale al campo elettrico
→
−
E:
→
−
P →
P →
eE
−
−
(
v
−
v
eτ →
i
−
i+1
m τ)
→
−
vd= i
= i
=− E
N
N
m
Ne segue che la densità di corrente che consegue il moto ordinato delle cariche
è pari a
ne2 τ →
−
→
−
−
j = −ne→
vd=
E
m
dove n è la densità di portatori di carica nel materiale considerato.
La costante di proporzionalità che lega la densità di carica e il campo elettrico
è definita conduttività e si indica con la lettera σ. In generale, considerando
portatori di carica di entrambi i segni presenti nello stesso materiale, σ assume
il valore
ne2 τ+
ne2 τ−
σ=
+
m+
m−
La conduttività σ è una proprietà che dipende dalla natura (massa) e dal
numero dei portatori di carica presenti nel materiale. Inoltre è facile intuire che
vi è una forte relazione con la temperatura: dallo stato di agitazione termica
dipendono infatti sia il libero cammino medio (e quindi τ ) che il numero di
portatori di carica.
L’inverso della conduttività si definisce resistività del materiale ed è una
grandezza misurata in [Ωm]. Tale grandezza può assumere valori in un ampio
range di ordini di grandezza (ρ = 10−8 ∼ 1017 [Ωm]). In base al valore di
resistività a temperatura ambiente, si possono classificare i diversi materiali in
conduttori (ρ = 10−8 ∼ 10−5 [Ωm]), semiconduttori (ρ = 100 ∼ 106 [Ωm]) e
isolanti (ρ = 108 ∼ 1017 [Ωm]).
La dipendenza di ρ dalla temperatura si manifesta in modo diverso a seconda
che il materiale sia un conduttore, un semiconduttore oppure un superconduttore. Nei metalli la dipendenza è pressochè lineare: all’aumentare della temperatura diminuisce la mobilità degli elettroni di conduzione e quindi aumenta ρ.
Nei semiconduttori l’effetto della diminuzione di mobilità dei portatori di carica
1.1 Introduzione e fisica dell’esperienza
3
viene compensato da un aumento degli stessi e conseguentemente la resistività
decresce. Esistono infine particolari materiali (molti dei quali sono materiali di
sintesi) che hanno un comportamento lineare sino a basse temperature, ma a
temperature prossime allo zero assoluto (si parla di temperatura critica) la loro
resistività crolla improvvisamente e tende ad un valore prossimo allo zero.
In natura esistono semiconduttori intrinseci costituiti da cristalli monoatomici (C, Si, Ge, Sn), biatomici (SiC, GaAs) o poliatomici: campioni purissimi
di tali materiali si comportano come semiconduttori. Solitamente si tratta di
cristalli contenenti atomi con quattro elettroni di valenza: il reticolo cristallino è quindi abbastanza stabile e non contiene elettroni di conduzione liberi. Il
campione è complessivamente neutro.
Si definisce Egap la differenza di energia tra la banda di valenza e la banda di conduzione, ovvero l’energia necessaria per estrarre l’elettrone e renderlo
disponibile come portatore di carica.
1.1.2
Drogaggi P e N
Semiconduttore
intrinseco
E
Semiconduttore
P
E
Semiconduttore
N
E
banda di conduzione
gap
gap
banda di conduzione
dell'accettore
banda di valenza
del donatore
gap
banda di valenza
Figura 1.1: Semiconduttori intrinseci e drogati: configurazione elettronica
Al fine di migliorare le caratteristiche di conducibilità dei semiconduttori
intrinseci (i quali manifestano spesso caratteristiche analoghe agli isolanti) è
possibile diffondere in essi piccole quantità di atomi di speci non appartenenti
al reticolo (impurità), al fine di ridurre il gap tra le bande di valenza e conduzione aggiungendo bande permesse prossime a quelle tipiche del semiconduttore intrinseco. In particolare è possibile drogare il cristallo con atomi trivalenti
(drogaggio P - aggiunta di una banda di valenza al di sotto della banda di
conduzione del semiconduttore) o pentavalenti (drogaggio N - aggiunta di una
banda di conduzione con energia di poco superiore a quella della banda di valenza del semiconduttore).
4
Effetto Hall nei semiconduttori
Se si inseriscono atomi pentavalenti (quali N, P, As, Sb) nel reticolo cristallino si ottiene un drogaggio N: gli atomi droganti sostituiscono quelli del materiale
originale, ma uno dei cinque elettroni di valenza del materiale drogante non è
necessario per formare il reticolo cristallino e resta libero da legami. Questo elettrone, qualora venga applicata una differenza di poteziale al campione, diventerà
un portatore di carica elettrica, potendosi spostare all’interno del reticolo.
In modo analogo si può drogare il campione con atomi trivalenti (quali B,
Al, Ga, In) i quali presentano tre elettroni nella banda di valenza e possono
quindi formare solo tre legami con gli altri atomi del reticolo. Si forma quindi
una lacuna, ovvero uno ione positivo. Anche la lacuna può spostarsi nel reticolo
cristallino e fungere quindi da portatore di carica positivo: in presenza di campo
elettrico infatti l’elettrone mancante viene acquisito da un atomo adiacente, che
a sua volta si trova in deficit di un elettrone e diventa quindi una nuova lacuna. Con questo meccanismo si può verificare una traslazione di cariche positive
virtuali (determinate dall’assenza di una carica negativa).
È utile ricordare che il drogaggio deve essere molto debole per non alterare
le caratteristiche del reticolo. Un campione drogato presenta quindi, a parità
di temperatura, una resistività minore rispetto al campione di semiconduttore
intrinseco. Inoltre si può verificare che il drogaggio determina il numero dei portatori di carica del tipo corrispondente al tipo di drogaggio, che per questo vengono detti portatori maggioritari; ma all’interno del reticolo si possono trovare
anche portatori di carica di segno opposto ad essi. Il numero dei portatori di
carica maggioritari è di parecchi ordini di grandezza superiore rispetto a quello
dei portatori minoritari e si verifica che
E
gap
3
√
√
√
nN pN = nP pP = nintrinseco pintrinseco = AT 2 e− 2KT
Si verifica quindi la dipendenza del numero di portatori di carica dalla temperatura, fenomeno evidente nel caso dei semiconduttori. Anche in un semiconduttore intrinseco (non ancora drogato) vi sono alcuni portatori di carica: si
tratta di coppie elettrone-lacuna che si creano e si annichilano con vite medie
dell’ordine di τ = 10−3 ∼ 10−8 [s].
La creazione di coppie può essere stimolata fornendo energia dall’esterno, ad
esempio mediante un fascio di fotoni di frequenza opportuna (Efotone = hν =
Egap ) oppure mediante il passaggio di una corrente elettrica elevata.
1.1.3
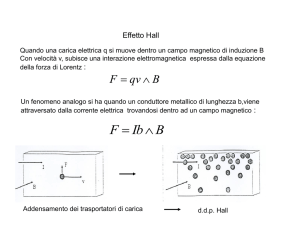
Effetto Hall nei semiconduttori
Un conduttore a forma di nastro sottile di sezione
Σ = ab
è percorso da una corrente di intensità i con verso concorde all’asse x.
→
−
Si definisce il vettore densità di corrente j come
→
−
−
j = ne→
vd
1.1 Introduzione e fisica dell’esperienza
5
y
z
y
B
e<0
z
e>0
a
--------
a
B
x
j
++++++++
Eel
b
EH
++++++++
x
j
Eel
b
EH
-------Figura 1.2: Effetto Hall con portatori di carica ±
dove n rappresenta i portatori di carica per unità di volume, e è la carica del−
l’elettrone, pari a 1.6 ∗ 10−19 C, e →
v d la velocità di deriva delle cariche. In
→
−
−
particolare se la superficie Σ è ortogonale a j , cioè a →
v d , si può scrivere:
i = jΣ
j=
i
Σ
cioè la densità di corrente è data dalla corrente che attraversa l’unità di superficie
lungo la perpendicolare alla direzione del moto delle cariche. Nel caso in esame
si scriverà
i −
→
−
−
ux
j = ne→
vd= →
ab
All’interno di un conduttore il vettore densità di corrente risulta sempre concorde all’asse x, indipendentemente dal segno dei portatori di carica.
→
−
Si sottopone il nastro all’azione di un campo magnetico uniforme B , che si
assume perpendicolare a j e concorde all’asse y. Allora su ciascun portatore di
carica agisce la forza di Lorentz:
→
−
→
−
−
F = e→
vd×B
La forza F , dovuta all’azione del campo magnetico su una carica in movimento, non è elettrostatica: si può quindi definire il campo elettromotore
→
−
→
−
F
j
→
−
→
−
→
−
−
=→
vd×B =
×B
EH =
e
ne
Esso è diretto lungo l’asse z e il suo verso dipende dal segno della carica: se
→
−
e > 0, E H è concorde all’asse z, mentre è discorde all’asse z se e < 0. Il campo
→
−
E H , anche chiamato campo di Hall dal nome del fisico che nel 1879 lo mise
per la prima volta in evidenza, modifica la traiettoria del moto delle cariche,
6
Effetto Hall nei semiconduttori
aggiungendo una componente trasversale alla velocità di deriva. L’effetto risultante è un accumulo di cariche di segno opposto sulle due facce del materiale
che sono ortogonali al campo stesso, cioè all’asse z.
→
−
Queste cariche danno origine ad un controcampo elettrostatico E el che si
oppone ad un ulteriore accumulo; la condizione di equilibrio è
→
−
→
−
E H + E el = 0
La differenza di potenziale generata ai capi del nastro lungo d dal campo
→
−
E H vale:
Z Q
→
−
→
−
−−→
→
−
−
V =
E H · d→
z = E H · P Q = ±E Hb
P
con segno positivo se e > 0, negativo se e < 0. In modulo la tensione di Hall
vale:
iB
Bb VA − VB
jBb
→
−
=
=
VH = E H b =
ne
nea
neρ
d
Il fenomeno descritto, chiamato effetto Hall trasversale, si presta ad alcune
interessanti applicazioni. Innanzitutto dal segno di VH si può determinare il
segno dei portatori di carica del materiale, e noti i moduli di VH e B si può
ricavare la densità di carica ne dei portatori. Utilizzando le relazioni
i=(
VA − V B
ab(VA − VB )
)=
R
ρd
con
R=
ρd
ρd
=
Σ
ab
si ricava l’espressione approssimata:
VH =
RH I →
−
B
d
dove RH è il coefficiente di Hall, dato per un conduttore dall’espressione:
RH =
1
ne
e per un semiconduttore da:
RH =
(µ2+ p − µ2− n)
e(µ+ p + µ− n)2
In queste formule si è indicato con n e p le concentrazioni volumetriche dei
portatori di carica (rispettivamente negativi e positivi) e con µ− e µ+ le rispettive mobilità.
Quindi RH è inversamente proporzionale alla densità dei portatori, dipende
dal materiale (e specialmente dalla temperatura) ed è legato alla mobilità dalla
relazione
µ = RH σ
1.1 Introduzione e fisica dell’esperienza
essendo σ la conduttività (ρ =
7
1
σ ).
La proporzionalità a n1 è causata, per una data corrente, dal fatto che minore è la densità dei portatori e più rapidamente ciascuno di essi si muove e
viene deflesso dal campo magnetico. Risulta perciò che il coefficiente di Hall
dei semiconduttori è di molti ordini di grandezza maggiore di quello dei metalli,
dato il numero molto minore dei portatori di carica liberi.
Nell’esperimento si userà un campione di Germanio, data la semplicità nel
fornire correnti di polarizzazione dell’ordine dei mA che danno tensioni di Hall
già dell’ordine dei mV, eliminando la necessità di amplificarle. Gli effetti della
temperatura sono rilevanti nei semiconduttori piuttosto che nei metalli poichè
la densità di elettroni e lacune è normalmente sufficientemente bassa da poterli
considerare un gas classico (non degenere).
Dalla Tensione di Hall, fornendo una relazione di proporzionalità tra la tensione VH e il modulo B del campo magnetico, possiamo costruire misuratori di
campo magnetico, detti sonde di Hall; la costante di proporzionalità
α=
i
b(VA − VB )
VH
=
=
B
nea
neρd
può essere determinata sperimentalmente, grazie a queste formule, introducendo
la sonda in un campo magnetico di valore noto e misurando il valore della
tensione di Hall.
1.1.4
Termocoppia
La termocoppia è uno strumento per la misura differenziale di temperatura. Il
suo funzionamento è spiegabile teoricamente mediante l’effetto Peltier e l’effetto Thomson, entrambi fenomeni termoelettrici che vengono sfruttati contemporaneamente per creare il cosiddetto effetto Seeback.
L’effetto Peltier si manifesta quando si applica una differenza di potenziale
ai capi di una giunzione composta di materiali diversi: si osserva che un estremo
della giunzione si riscalda, metre l’altro si raffredda cedendo energia alla prima.
Invertendo il verso della corrente il fenomeno si inverte e quindi non si può attribuire l’evidenza sperimentale all’effetto Joule.
Per mantenere costante la temperatura della giunzione è necessario fornire
una potenza
P = π1.2 i
dove π è il coefficiente di Peltier e i è la corrente circolante nella giunzione.
Se si inverte il verso della corrente la potenza resta uguale in modulo e il
coefficiente di Peltier si inverte, π1.2 = −π2.1 . L’effetto Peltier è dunque reversibile. Per convenzione si assume positivo il segno di π1.2 quando la corrente,
passando dal materiale 1 al materiale 2, produce un assorbimento di potenza,
come se agisse una tensione tra i due punti della giunzione in verso concorde
8
Effetto Hall nei semiconduttori
2
1
1
Figura 1.3: Effetto Peltier
con la corrente circolante nella stessa.
Il coefficiente di Peltier è a tutti gli effetti una tensione, il cui valore dipende
dalla natura dei due materiali di cui è composta la giunzione. Tale effetto è
dovuto a differenze nelle distribuzioni delle energie elettroniche che a temperature superiori allo zero assoluto sono superiori nei metalli all’energia di Fermi e
si differenziano a seconda del materiale considerato. Questo effetto può essere
sfruttato per costruire serbatoi di calore.
L’effetto Thomson prevede che se si mantiene su un conduttore (rettilineo)
un gradiente di temperatura, sia possibile verificare uno scambio termico non
spiegabile mediante il solo effetto Joule. Le verifiche sperimentali sono compatibili con un incremento virtuale del potenziale lungo il conduttore, proporzionale
al gradiente di temperatura:
∂T
∂V
=σ
∂s
∂s
Il coefficiente di proporzionalità σ dipende dalla temperatura e dal materiale di
cui è composto il conduttore.
Si ha assorbimento di potenza se il gradiente del potenziale è parallelo alla
corrente circolante nel conduttore, dissipazione in caso contrario.
La rivelazione sperimentale di questo fenomeno è complicata, in quanto percentualmente la potenza dissipata è minore rispetto alla potenza prodotta per
effetto Joule. Infatti i valori tipici del coeffieciente di Thomson σ sono dell’ordine
di 10−6 [V K −1 ]. Inoltre è da notare che in un circuito chiuso composto da un
unico materiale l’effetto Thomson non produce alcuna forza elettromotrice, tuttavia si possono misurare alterazioni delle distribuzioni energetiche locali degli
1.1 Introduzione e fisica dell’esperienza
9
elettroni.
Si consideri invece un circuito composto da due metalli diversi, privo di generatore e si mantengano le due giunzioni A e B a temperature diverse TA e
TB : inserendo un amperometro all’interno del circuito si rivela in questo caso
un passaggio di corrente, dovuto alla presenza di una forza elettromotrice. Tale
fenomeno è conosciuto come effetto Seeback e la forza elettromotrice è di natura
temolettrica.
P
Q
1
1
A
2
B
Figura 1.4: Effetto Seeback
Si può spiegare questo effetto considerando il fatto che nei diversi metalli
si hanno diversi lavori di estrazione, ovvero l’energia necessaria per strappare
un elettrone da uno stato legato ad una banda di conduzione è una grandazza
dipendente dalla configurazione atomica dei due metalli. Tale grandezza è inoltre dipendente dalla temperatura alla quale si trovano le giunzioni, in quanto
la temperatura è indice dell’energia interna posseduta dal metallo. A parità di
condizioni un corpo ad una temperatura maggiore possiede un’energia interna
maggiore rispetto ad un corpo più freddo e quindi un lavoro di estrazione minore.
Si genera quindi una diffusione di cariche tra le giunzioni e un conseguente
passaggio di corrente. Se si mantiene una giunzione ad una temperatura di riferimento TA e si varia la temperatura della seconda giunzione TB = T si osserva
che la forza elettromotrice varia con andamento parabolico con un massimo in
T = Tn = (TA + Ti )/2. Inoltre si verifica un punto di inversione della grandezza
per T = Ti . La derivata della forza termoelettrica dE/dT , funzione della temperatura, è detta potere termoelettrico.
Si verifica che nelle due giunzioni si hanno effetti Peltier, mentre nei conduttori effetti Thomson. Si indichi con T0 la temperatura dei punti P e Q tra i
10
Effetto Hall nei semiconduttori
quali è posto lo strumento di misura, si ha
VQ = V P +
Z
TA
σ1 dT + π1.2 (TA ) +
T0
Z
TB
σ2 dT + π2.1 (TB ) +
TA
Z
T0
σ1 dT
TB
semplificando i termini opposti si ha
E = VQ − VP = π1.2 (TA ) − π2.1 (TB ) +
Z
TB
TA
(σ2 − σ1 )dT
In questa formula si evidenzia come la forza termoelettrica nasca dalla differenza tra le f.e.m. di Peltier alle due giunzioni e dalla differenza dei coefficienti
di Thomson nei due metalli.
Questo effetto viene sfruttato per eseguire misure differenziali di temperatura: una giunzione viene matenuta ad una temperatura fissa, immergendola
ad esempio in un bagno di ghiaccio fondente, mentre la seconda giunzione costituisce la sonda per misurare la temperatura. Tali sonde forniscono risposte
pronte e precise, inoltre possono essere applicate in range ampi di temperatura. Nell’esperienza verrà utilizzata una giunzione ferro-costantana, per la quale
il potere termoelettrico è circa dE/dT = 5 · 10− 5 [V/K]. La taratura avviene
fornendo una f.e.m. opposta a quella generata dalla termocoppia, regolata in
modo tale da fornire una lettura nulla quando le due giunzioni siano alla stessa
temperatura.
1.2
1.2.1
Caratterizzazione del campo magnetico
Setup sperimentale
Per il principio di Ampére, quando una spira composta da materiale conduttore
viene attraversata da una corrente elettrica (cariche elettriche in moto), essa
diventa sorgente di un campo magnetico. Se si considera un solenoide, i campi
prodotti dalle singole spire si sommano e danno origine ad un campo magnetico
con intensità massima sull’asse del solenoide. Per punti prossimi all’asse del
solenoide inoltre si può verificare teoricamente la presenza di linee di campo
magnetico pressoché parallele allo stesso. Allontanandosi dall’asse le linee del
campo si flettono e si chiudono all’esterno del solenoide. In tal modo è possibile
costruire dei magneti, il cui campo può essere controllato in intensità variando
la corrente circolante nelle spire.
Nell’esperienza si utilizza un elettromagnete composto da due solenoidi avvolti ad un unico traferro di materiale ferromagnetico. Il campo prodotto dalle
due bobine induce una magnetizzazione nel materiale ferromagnetico di cui è
composto il traferro, quindi genera un secondo campo magnetico tra le espansioni del traferro. La prima parte dell’esperienza prevede la caratterizzazione
del campo magnetico nei pressi delle espansioni del traferro.
Per la misura del campo magnetico occorre utilizzare un teslametro digitale,
dotato di sonda ad effetto Hall. Tale sonda è sensibile solo in una zona prossima
1.2 Caratterizzazione del campo magnetico
11
all’estremità, inoltre occorre prestare attenzione all’orientamento della sonda,
in quanto essa misura il flusso del campo magnetico sulla superficie sensibile,
quindi piccole inclinazioni della superficie possono variare i risultati.
Si collega il generatore di tensione ai solenoidi, posti in serie, avendo cura
di verificare che il campo prodotto dalla somma dei campi delle singole bobine
sia non nullo (i campi devono avere versi concordi). Al fine di assicurare una
corrente costante di circa 2 A durante tutta la misura, occorre misurare il valore
Ib della corrente di eccitazione dei solenoidi, utilizzando un amperometro posto
in serie nel circuito. Non è opportuno superare per lunghi periodi di tempo la
soglia di 2 A, come corente nei solenoidi, al fine di prevenire il surriscaldamento
degli stessi (in tal caso ci si aspetta un campo di circa 300 [T]).
La misura del campo deve essere eseguita in una matrice di punti giacenti sul
piano mediano delle espansioni dell’elettrocalamita. Per il posizionamento della
sonda si ha a disposizione un supporto. La misura della posizione del sensore
non può essere molto precisa a causa della difficoltà di lettura tra le espansioni
e dell’impossibilità di localizzare sulla superficie della sonda un preciso punto di
misura. Secondo il manuale allegato al teslametro utilizzato la sonda è sensibile
infatti in un range di circa 1 cm, calcolato a partire da 1 mm dall’estremità.
Appare quindi chiaro che la misura del campo, pur essendo molto precisa come
valore di intensità, può fornire unicamente un andamento di massima dello stesso, utile per individuare il punto di massimo valore del campo tra le espansioni.
Osservando la geometria delle linee di campo teoriche e le simmetrie di cui gode
il problema si può ipotizzare infatti che il campo sia massimo nel punto centrale
delle espansioni del magnete.
+
Figura 1.5: Elettromagnete
12
Effetto Hall nei semiconduttori
1.2.2
Acquisizione dati
Le misure delle dimesioni fisiche delle espansioni del magnete sono state eseguite
utilizzando un calibro con sensibilità pari a 1/20 mm. È stata verificata una
leggera inclinazione relativa delle espansioni: si è scelto di considerare un errore
più grande della sensibilità dello strumento, al fine di poter considerare le facce
parallele.
Si è indicato come asse x l’asse verticale, y l’asse orizzontale. Non sono
state eseguite misure lungo la direzione ortogonale alle facce dell’elettromagnete, essendo lo spazio tra le stesse troppo esiguo. Inoltre dato il rapporto tra
la distanza tra le espansioni e il lato delle stesse (si tratta di facce quadrate) si
può supporre che le linee di campo siano ortogonali alle facce (almeno all’interno
delle stesse) e che il modulo del campo lungo l’asse z sia costante.
lx = ly = 40.10 ± 0.05[mm]
d = 7.90 ± 0.05[mm]
Nel manuale d’uso del teslametro sono indicate le sensibilità dello strumento
e della sonda utilizzate. Prima di procedere con la misura occorre azzerare lo
strumento, seguendo la procedura indicata nel manuale, accertandosi di aver
tolto la sonda dalle espansioni del magnete al fine di evitare l’interazione con
correnti parassite eventualmente presenti nel traferro. Lo strumento deve essere mantenuto acceso per un periodo di 15 minuti circa al fine di stabilizzare
la temperatura del sensore (warm-up del sensore), il quale si scalda per effetto
Joule ed è sensibile a variazioni di temperatura, secondo quanto riportato nella
documentazione dello strumento.
Risoluzione:
• range: 30 mT - risoluzione: 0.01 mT
• range: 300 mT - risoluzione: 0.1 mT
• range: 3 T - risoluzione: 1 mT
Tempo di warm-up: 15 minuti.
Accuratezza della sonda per differenze di temperatura: -0.05 percento ogni
grado centigrado.
Dopo aver collegato i solenoidi in serie e acceso il generatore (si utilizzano
le boccole + e -, non collegando il ground) si è impostata una corrente di eccitazione, misurata tramite un multimetro digitale. Tale corrente deve rimanere
costante durante l’intero arco della misura, devono quindi essere compensate
eventuali variazioni agendo sul potenziometro presente nell’alimentatore. La diminuzione della corrente è un fenomeno evidente soprattutto per alti valori di Ib :
questo fatto è spiegabile considerando che le bobine generanti il campo sono costituite da conduttori ohmici, nei quali aumenta la resitività all’aumentare della
temperatura per effetto Joule. Regolando quindi l’alimentazione in tensione si
assiste ad una diminuzione della corrente circolante nel circuito all’aumentare
1.2 Caratterizzazione del campo magnetico
13
della temperatura dello stesso. Per controllare questo fenomeno occorre variare la tensione di alimentazione in modo opportuno. In alternativa è possibile
utilizzare una generatore di corrente variabile, sostituendolo al generatore di
tensione, tuttavia il regolatore di corrente presente nel laboratorio non permetteva di ottenere correnti e tensioni tali da ottenere un campo magnetico di
entità sufficiente nella seconda parte dell’esperienza.
Ib = 1.468 ± 0.001[A]
Nell’eseguire la misura di posizione della sonda è stata considerata un’incertezza pari a 1 mm sulle misure, essendo stata utilizzata una normale squadretta. La posizione della sonda è stata valutata sul bordo inferiore della stessa per
le misure lungo l’asse y e a una distanza di 1 mm dall’estremità della stessa.
x [mm]
±0.1
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
y [mm]
±0.1
-1.6
-0.8
0.0
0.8
1.6
2.4
3.2
4.0
4.8
5.6
B [mT]
±0.1
33.6 0.1
69.5
231.2
258.2
257.4
258.7
250.6
248.9
98.4
37.9
x [mm]
±0.1
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
y [mm]
±0.1
-1.6
-0.8
0.0
0.8
1.6
2.4
3.2
4.0
4.8
5.6
B [mT]
±0.1
48.7
97.0
260.2
291.8
292.4
292.1
291.8
260.9
95.3
38.7
x [mm]
±0.1
4.0
4.0
4.0
4.0
4.0
4.0
4.0
4.0
4.0
4.0
y [mm]
±0.1
-1.6
-0.8
0.0
0.8
1.6
2.4
3.2
4.0
4.8
5.6
B [mT]
±0.1
45.4
89.5
278.9
301.1
301.1
301.1
299.1
201.2
67.0
35.8
Tabella 1.1: Uniformità del campo tra le espansioni del magnete
1.2.3
Risultati
Graficando i dati ottenuti di campo in funzione della coordinata spaziale, (vedere
le figure 1.6 e 1.7) è possibile osservare un massimo di intensità del campo nei
pressi dell’asse comune alle espansioni dell’elettromagnete. Un campo particolarmente intenso nel bordo inferiore può essere infatti attribuito al campo
magnetico generato dai solenoidi, ma tuttavia non imputabile all’azione del traferro.
Nella regione centrale si notano variazioni di intensità del campo maggiori
della sensibilità dello strumento utilizzato. Si calcola quindi la deviazione standard dei dati che fornisce una stima dell’incertezza associata alle misure di
campo magnetico effettuate attraverso la sonda di Hall. Un’ulteriore fonte di
incertezza è dovuta all’impossibilità di determinare con precisione la posizione
spaziale della sonda di Hall e all’impossibilità di garantire che tale posizione non
vari durante l’esecuzione dell’esperienza.
Per valutare un valore medio sono stati selezionati solamente i valori di
campo nella regione centrale (dove si è osservata una distribuzione pressoché
costante). I valori ottenuti sono i seguenti:
Pn
Bi
< B >= i=1
= 0.283[T ]
n
14
Effetto Hall nei semiconduttori
-1.6
-0.80.
x @cmD
0.8
1.6
2.4
3.2
4.
4.8
5.6
300
200
100
B @mTD
0
4.
2.
y @cmD
0.
Figura 1.6: Andamento del campo magnetico tra le espansioni del magnete
y @cmD
4.
2.
0.
300
B @mTD
200
100
0
-1.6 -0.8
0.
0.8
1.6
2.4
x @cmD
3.2
4.
4.8
5.6
Figura 1.7: Andamento del campo magnetico tra le espansioni del magnete
σB =
Pn
< B >)2
= 0.020[T ]
n−1
σB
= √ = 0.006[T ]
n
i=1 (Bi −
σ<B>
Si è scelto di posizionare la sonda ed i semiconduttori nella seconda parte
dell’esperienza all’incirca al centro dei poli del magnete anche considerando che,
per ragioni di simmetria del traferro, in tale punto le linee di campo sono rettilinee e ortogonali alle facce dell’elettromagnete. Il campo infatti ha linee di
campo rettilinee nello spazio compreso tra le espansioni, mentre al di fuori di
esso gli effetti di bordo implicano l’esistenza di linee di campo incurvate. All’esterno di tale spazio tuttavia abbiamo verificato un rapido calo dell’intensità
1.3 Misura del ciclo di isteresi magnetica del traferro
15
del campo, come si può apprezzare osservando il grafico.
1.3
Misura del ciclo di isteresi magnetica del
traferro
Il fenomeno dell’isteresi magnetica in materiali ferromagnetici prevede che immergendo in un campo magnetico variabile un oggetto con tali caratteristiche
la magnetizzazione e quindi il campo magnetico indotto nello stesso segua una
dipendenza lineare dal campo variabile. Il campo indotto nel materiale ferromagnetico, quale è il traferro dell’elettromagnete, arriva ad una soglia di saturazione aumentando oltre un certo limite il campo sorgente, che corrisponde ad
un comportamento non più lineare della magnetizzazione, funzione del campo
magnetico variabile. Riducendo quest’ultima grandezza tuttavia si verifica la
presenza di una magnetizzazione residua che può essere azzerata invertendo il
segno della sorgente del campo. Tale processo può essere ripetuto per valori di
campo di segno opposto e si possono eseguire dei cicli di isteresi completi. Lo
scopo di questa parte dell’esperienza consiste nel determinare una corrispondenza, all’interno della zona di comportamento lineare, tra la corrente circolante nei
solenoidi Ib , responsabile del campo magnetico variabile e il modulo del campo
magnetico indotto tra le espansioni dell’elettromagnete.
1.3.1
Setup sperimentale
A
+
al teslametro
Area sensibile
Hall
Figura 1.8: Setup sperimentale: misura del ciclo di isteresi magnetica del
traferro
Per eseguire questa prova occorre tarare opportunamente il teslametro e
porre la sonda tra le espansioni del magnete, fissandola in posizione mediante
16
Effetto Hall nei semiconduttori
un supporto stabile.
Il magnete deve essere alimentato con una corrente variabile mediante un
potenziometro: a tale scopo è stato utilizzato un alimentatore regolabile. In
serie ai solenoidi è stato collegato un multimetro digitale, al fine di monitorare
la corrente circolante nelle bobine Ib .
La corrente massima di alimentazione delle bobine non deve superare i 2 A
per lunghi periodi di tempo.
1.3.2
Acquisizione dati
Sono state utilizzate le uscite duali dell’alimentatore (contrassegnate dalle boccole ± 15V). La misura è stata eseguita da un valore di tensione (quindi di
corrente) prossimo allo zero, aumentando la corrente a step fissi sino a 2 A,
quindi è stata eseguita una rampa discendente. Per invertire il campo magnetico è stata invertita l’alimentazione sui solenoidi. Il ciclo è stato ripetuto per
tre volte, misurando ad ogni step di corrente il corrispondente valore del campo
magnetico indotto.
Tratto iniziale
Ib [mA]
B [mT]
± 0.001
0.029
0.198
0.399
0.603
0.810
1.003
1.201
1.405
1.609
1.806
2.017
12.02
42.6
81.5
120.9
164.4
205.7
242.1
280.0
319.0
355.0
396.0
Discesa
Ib [mA]
B [mT]
± 0.001
2.017
1.796
1.598
1.392
1.180
0.990
0.805
0.596
0.399
0.198
0.030
396
367
329
292.8
251.3
213.2
175.6
132.5
91.8
49.3
15.37
Discesa
Ib [mA]
B [mT]
± 0.001
-0.031
-0.205
-0.415
-0.603
-0.816
-1.017
-1.212
-1.409
-1.612
-1.823
-2.010
2.71
-35.2
-76.6
-115.5
-160.6
-200.4
-240.9
-279.5
-321
-360
-395
Salita
Ib [mA]
B [mT]
± 0.001
-2.010
-1.822
-1.595
-1.389
-1.196
-0.992
-0.792
-0.601
-0.398
-0.198
-0.030
-395
-371
-331
-292.4
-254.2
-212.6
-172.2
-132.3
-90.8
-47.6
-14.47
Salita
Ib [mA]
B [mT]
± 0.001
0.029
0.205
0.404
0.613
0.795
0.995
1.205
1.415
1.615
1.809
2.004
-2.10
34.1
76.3
118.7
157.5
199.6
239.3
281.4
319.0
361.0
393
Tabella 1.2: Ciclo di isteresi 1
Discesa
Ib [mA]
B [mT]
± 0.001
2.004
393
1.800
362
1.590
330
1.400
292.7
1.195
254.1
0.990
212.8
0.785
171.0
0.595
132.0
0.393
89.7
0.206
48.6
0.029
14.76
Discesa
Ib [mA]
B [mT]
± 0.001
-0.030
2.36
-0.204
-35.5
-0.404
-75.0
-0.602
-115.9
-0.806
-159.4
-1.020
-201.9
-1.201
-239.9
-1.399
-278.1
-1.606
-321
-1.793
-357
-1.998
-394
Salita
Ib [mA]
B [mT]
± 0.001
-1.998
-394
-1.793
-367
-1.601
-335
-1.394
-295.6
-1.186
-254.0
-0.994
-214.9
-0.802
-174.0
-0.590
-131.5
-0.402
-92.5
-0.201
-48.0
-0.030
-15.38
Salita
Ib [mA]
B [mT]
± 0.001
0.029
-2.9
0.207
33.7
0.413
76.5
0.614
117.7
0.809
159.6
1.002
196.8
1.206
238.5
1.401
277.5
1.600
316
1.809
357
2.014
394
Tabella 1.3: Ciclo d’isteresi 2
1.3.3
Risultati
Dalle singole curve è stata estratta una zona di linearità per il tratto discendente
e una per quello ascendente. In queste zone sono stati valutati, con il metodo
1.3 Misura del ciclo di isteresi magnetica del traferro
Discesa
Ib [mA]
B [mT]
± 0.001
2.014
394
1.797
367
1.596
329
1.398
292.0
1.199
254.6
1.011
216.7
0.796
172.8
0.597
130.0
0.400
88.7
0.189
47.9
0.029
14.69
Discesa
Ib [mA]
B [mT]
± 0.001
-0.029
2.21
-0.218
-36.6
-0.410
-76.2
-0.605
-116.5
-0.803
-160.1
-1.015
-200.8
-1.203
-239.7
-1.412
-280.9
-1.598
-318.0
-1.816
-359
-2.007
-395
Salita
Ib [mA]
B [mT]
± 0.001
-2.007
-395
-1.799
-369
-1.604
-331
-1.400
-294.9
-1.200
-255.3
-0.995
-214.0
-0.798
-173.2
-0.602
-133.3
-0.395
-90.5
-0.193
-48.7
-0.031
-14.78
17
Salita
Ib [mA]
B [mT]
± 0.001
0.029
-2.10
0.206
33.0
0.405
76.2
0.610
117.5
0.815
158.2
0.998
195.9
1.202
238.2
1.405
278.1
1.602
316
1.808
355
2.002
393
Tabella 1.4: Ciclo d’isteresi 3
dei minimi quadrati, fit lineari di B=f(Ib ). I coefficienti di ciascun fit, risultati
compatibili mediante tests normali, sono stati mediati tra loro per ottenere una
curva di taratura del campo magnetico indotto in ciascun ciclo. Infine tutti i
risultati sono stati mediati per ottenere un’unica curva di taratura del campo.
Il tratto iniziale del primo ciclo non è stato considerato nell’esecuzione delle
interpolazioni. Come già riportato in precedenza, l’errore associato alle misure
di campo non è la sensibilità dello strumento (una unità sull’ultima cifra significativa) ma la deviazione standard calcolata nella prima parte dell’esperienza.
Primo ciclo di isteresi
Per selezionare i dati nella zona di linearità sono stati disegnati in un grafico
(vedi figura 1.9) i risultati delle misure eseguite; in seguito il range dei valori è
stato ridefinito dopo aver disegnato le curve interpolanti.
B @TD
0.4
0.2
-2
-1
1
2
IB @AD
-0.2
-0.4
Figura 1.9: Primo ciclo di isteresi: dati raccolti nelle misure sperimentali
18
Effetto Hall nei semiconduttori
Al fine di selezionare correttamente il set di dati da utilizzare è stato eseguito
il calcolo del coefficiente di correlazione lineare nel tratto di discesa del primo
ciclo:
Pn
(xi − < x >)(yi − < y >)
ρ = pPn i=1
= 0.999
Pn
2
2
i=1 (xi − < x >)
i=1 (yi − < y >)
Da questa analisi emerge che il set di dati considerato è fortemente correlato
ed è quindi corretto procedere con un’interpolazione lineare dei dati sperimentali.
Nel seguito verranno richiamate brevemente le formule utilizzate per il calcolo della retta di interpolazione:
y = a + bx
è la retta di interpolazione della quale saranno calcolati i coefficienti a e b.
a
A=
b
P n 1 P n xi !
D=
i=1 σi2
xi
i=1 σi2
Pn
B=
i=1 σi2
x2i
i=1 σi2
Pn
P n yi !
2
Pni=1 xσi yi i
i=1 σi2
E = D−1
DA = B → A = D−1 B
!
Pn x2i
Pn
− i=1 σx2i
1
i=1 σi2
Pn
Pn 1 i
=
∆
− i=1 σx2i
i=1 σi2
i
√
σa = √ E1.1
σb = E2.2
Nel caso preso in esame si ottengono i seguenti valori:
a = (0.0084 ± 0.0014)[T ]
b = (0.2047 ± 0.0014)[T A−1]
Per valutare l’attendibilità del fit lineare appena eseguito un test del χ2 ,
calcolandone il valore ridotto:
Pn yi −a−bxi 2
)
i=1 (
σi
2
χ =
= 0.13
DF
I gradi di libertà del sistema sono 16. Per DF = 16 e al livello di confidenza
del 5% il test si considera riuscito: la probabilità di ottenere il valore di χ2
ridotto 0.13 è superiore al 90%.
Con procedimento analago è stata interpolata la fase con corrente crescente
del ciclo, ottenendo i seguenti risultati:
ρ = 0.999
a = (−0.0078 ± 0.0014)[T ]
b = (0.2048 ± 0.0014)[T A−1]
χ2 = 0.12
DF = 16 → χ2critico = 1.6
1.3 Misura del ciclo di isteresi magnetica del traferro
19
Anche in questo caso il test del χ2 conferma la validità dell’interpolazione lineare calcolata.
Al fine di determinare per questo ciclo di isteresi un’unica retta di calibrazione sono stati confrontati i coefficienti delle due rette trovate, per verificarne il parallelismo. Poichè si tratta di valori sperimentali e non teorici sarebbe
opportuno utilizzare un test di Student. Ma i gradi di libertà complessivi del
sistema sono 32 (16+16): per DF > 30, ovvero grandi popolazioni, il test di
Student fornisce gli stessi risultati del test normale: per il parametro b quindi è
stata costruita la variabile normale centrata e ridotta
|b1 − b2 |
z=p
= 0.092
σ12 + σ22
Il valore limite per z, al limite di confidenza del 5%, è 1.96: il test dà esito
positivo e quindi i due coefficienti angolari sono tra loro confrontabili. Non
ha senso invece effettuare un test simile per i valori del termine noto: le due
rette infatti intersecano l’asse y rispettivamente una sopra l’origine e l’altra
sotto, quindi è logico aspettarsi che i termini noti siano due numeri diversi non
confrontabili tra loro. Il loro valore medio, però, deve essere un numero prossimo
allo zero. Si procede mediando i valori ottenuti nei due tratti attraverso una
media pesata e si ottiene
< a >= (0.0003 ± 0.0009)[T ]
< b >= (0.2048 ± 0.0010)[T A−1]
Secondo ciclo di isteresi
In questo ciclo di isteresi è stato ripetuto il calcolo dei parametri relativi alle
rette di interpolazione con modalità analoghe a quanto descritto in precedenza.
La validità dei risultati trovati è confermata dall’esito dei test statistici utilizzati
(test del χ2 ridotto, test normale).
Tratto a corrente decrescente:
ρ = 0.999
a = (0.0075 ± 0.0014)[T ]
b = (0.2049 ± 0.0014)[T A−1]
χ2 = 0.10
DF = 16 → χ2critico = 1.6
Tratto a corrente crescente:
ρ = 0.999
a = (−0.0091 ± 0.0014)[T ]
b = (0.2051 ± 0.0014)[T A−1]
χ2 = 0.08
DF = 16 → χ2critico = 1.6
Calcolo della retta di calibrazione media:
z = 0.08
< a >= (−0.0008 ± 0.0009)[T ]
< b >= (0.2050 ± 0.0010)[T A−1]
20
Effetto Hall nei semiconduttori
B @TD
0.4
0.2
-2
-1
1
2
IB @AD
-0.2
-0.4
Figura 1.10: Secondo ciclo di isteresi: dati raccolti nelle misure sperimentali
Terzo ciclo di isteresi
In questo ciclo di isteresi è stato ripetuto il calcolo dei parametri relativi alle
rette di interpolazione con modalità analoghe a quanto descritto in precedenza.
La validità dei risultati trovati è confermata dall’esito dei test statistici utilizzati
(test del χ2 ridotto, test normale).
B @TD
0.4
0.2
-2
-1
1
2
IB @AD
-0.2
-0.4
Figura 1.11: Terzo ciclo di isteresi: dati raccolti nelle misure sperimentali
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
21
Tratto a corrente decrescente:
ρ = 0.999
a = (0.0075 ± 0.0014)[T ]
b = (0.2045 ± 0.0014)[T A−1]
χ2 = 0.12
DF = 16 → χ2critico = 1.6
Tratto a corrente crescente:
ρ = 0.999
a = (−0.0087 ± 0.0014)[T ]
b = (0.2042 ± 0.0014)[T A−1]
χ2 = 0.11
DF = 16 → χ2critico = 1.6
Calcolo della retta di calibrazione media:
z = 0.15
< a >= (−0.0006 ± 0.0009)[T ]
< b >= (0.2043 ± 0.0010)[T A−1]
Retta di calibrazione finale
Al fine di determinare un’unica retta di calibrazione dell’intensità del campo
magnetico B = B(IB ) è stata eseguita una media pesata dei valori dei parametri
medi stimati in ciascun ciclo, ottenendo (dopo aver verificato la consistenza di
tali stime) i seguenti parametri (vedi figura 1.12):
< a >= (−0.350 ± 0.003)[mT ]
< b >= (0.2047 ± 0.0006)[T A−1]
Poichè l’errore calcolato attraverso la propagazione è troppo piccolo per essere una reale stima dell’escursione delle misure si associa al coefficiente a come
errore l’escursione tra il valore medio e quello calcolato:
∆a = 0.008
B = (−0.000 ± 0.008) + (0.2047 ± 0.0006)IB [T ]
Ulteriore documentazione riguardo i calcoli svolti può essere reperita nell’appendice contenente l’intero notebook utilizzato per l’analisi statistica.
1.4
1.4.1
Misura dell’effetto Hall - semiconduttore di
tipo N
Setup sperimentale
Per la misura dell’effetto Hall si utilizza un campione di germanio drogato N,
a forma di parallelepipedo. Su due facce opposte sono saldati, mediante una
lega di Sn-Pb, i contatti per fornire corrente al campione, mentre su altre due
facce sono saldati tre contatti per la lettura della tensione di Hall. Sui contatti
presenti sulla stessa faccia è collegato un ponte resistivo regolabile mediante un
22
Effetto Hall nei semiconduttori
B @TD
0.3
0.2
0.1
-1.5
-1
-0.5
0.5
1
1.5
IB @AD
-0.1
-0.2
-0.3
Figura 1.12: Retta di calibrazione finale B = B(IB )
Alimentazione del magnete
A
+
Misura di R
Norma
+
+
18,0V
out
generatore di
corrente costante
-
Metex
VH
A
campione di
germanio
Figura 1.13: Setup sperimentale: misura dell’effetto Hall
potenziometro che permette di eliminare errori sistematici dovuti alla presenza
di differenza di potenziale tra i due punti di misura non perfettamente allineati
su un asse ortogonale alla direzione della corrente.
I cinque cavi del campione sono collegati ad una basetta su cui è montato il
ponte resistivo e le boccole di alimentazione. Al campione deve essere garantita
un’alimentazione con corrente costante, per questo scopo è necessario utilizzare
il generatore di corrente costante, collegato al generatore di tensione a 12 V.
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
23
La corrente circolante nel campione deve essere misurata con precisione mediante uno strumento digitale, mentre per la misura della tensione di Hall occorre
un millivoltmetro ad alta impedenza di ingresso, in modo da ridurre l’errore di
misura sistematico.
Dopo aver azzerato il ponte e aver posizionato il campione all’interno delle
espansioni del magnete (in modo tale che i contatti per la misura dell’effetto Hall siano ortogonali alle linee del campo) si possono alimentare i solenoidi
variando la corrente a step fissi e misurando Ib . Per ciascun valore di corrente
circolante nei solenoidi si eseguono alcune misure variando la corrente circolante
nel campione (da 0 a 10 mA), quindi si può invertire il campo magnetico, invertendo la polarità dell’alimentazione del solenoide. Le misure devono quindi
essere ripetute anche con il campo magnetico orientato in verso opposto.
Per alti valori (in modulo) di corrente nei solenoidi è importante verificare che
la misura di questa grandezza rimanga costante durante l’esecuzione dell’intero
set di misure. Effetti di riscaldamento delle bobine possono infatti portare variazioni di questa grandezza che devono essere corretti agendo sul potenziometro
che regola il voltaggio di alimentazione.
È importante non superare per tempi lunghi il valore di 10 mA come corrente di alimentazione del campione (Ic ), al fine di prevenire surriscaldamenti e
danneggiamenti.
Per poter valutare il coefficiente RH servono inoltre le dimensioni fisiche del
campione utilizzato e una misura di resistività dello stesso, eseguita valutando
tensione e corrente circolante in esso.
1.4.2
Acquisizione dati
In primo luogo sono state reperite le caratteristiche fisiche del campione nelle
apposite tabelle:
spessore: d = (2.00 ± 0.01)[mm]
larghezza: A = (4 ± 1)[mm]
lunghezza: L = (28 ± 1)[mm]
La valutazione della resistenza del campione al fine di valutare la resistività
è stata ripetuta più volte per ridurre l’incertezza su tale misura, quindi è stata
eseguita una media del valore ottenuto ed è stato valutato l’errore corrispondente.
R = (68.61 ± 0.14)[Ω]
ρ = (0.020 ± 0.005)[Ωm]
Il campione è stato posizionato nel centro delle espansioni del magnete ed è
stato fissato in posizione mediante un supporto rigido. Il ponte è stato azzerato
mentre il campione si trovava al di fuori delle espansioni dei magneti.
Dopo aver eseguito i collegamenti necessari è iniziata la fase di misura, procedendo a step fissi di Ib e variando ad ogni step la corrente nel campione Ic .
24
Effetto Hall nei semiconduttori
Quindi è stato invertito il campo magnetico e le misure sono state ripetute.
Ic [mA]
± 0.01
3.26
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
1.61
1.73
1.97
2.20
2.45
2.69
2.94
3.17
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
3.42
3.66
3.91
4.14
4.39
4.64
4.88
Ic [mA]
± 0.01
-3.28
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
-1.57
-1.68
-1.94
-2.15
-2.40
-2.65
-2.88
-3.13
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
-3.38
-3.62
-3.86
-4.09
-4.34
-4.58
-4.82
Tabella 1.5: Germanio tipo N: Ib 1.600 ± 0.001 A
Ic [mA]
± 0.01
3.26
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
1.38
1.48
1.70
1.90
2.12
2.33
2.53
2.75
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
2.96
3.16
3.38
3.59
3.81
4.01
4.22
Ic [mA]
± 0.01
-3.24
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
-1.36
-1.47
-1.68
-1.89
-2.10
-2.31
-2.50
-2.72
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
-2.92
-3.15
-3.34
-3.56
-3.77
-4.00
-4.20
Tabella 1.6: Germanio tipo N: Ib 1.300 ± 0.001 A
Ic [mA]
± 0.01
3.26
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
1.09
1.18
1.35
1.51
1.68
1.85
2.00
2.19
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
2.35
2.52
2.69
2.85
3.02
3.19
3.35
Ic [mA]
± 0.01
-3.27
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
-1.08
-1.16
-1.33
-1.49
-1.66
-1.83
-1.99
-2.16
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
-2.33
-2.50
-2.65
-2.83
-3.00
-3.16
-3.33
Tabella 1.7: Germanio tipo N: Ib 1.000 ± 0.001 A
Ic [mA]
± 0.01
3.28
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
0.81
0.86
0.99
1.12
1.24
1.36
1.49
1.60
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
1.73
1.85
1.97
2.10
2.22
2.33
2.46
Ic [mA]
± 0.01
-3.28
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
-0.79
-0.83
-0.96
-1.09
-1.20
-1.33
-1.46
-1.58
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
Tabella 1.8: Germanio tipo N: Ib 0.700 ± 0.001 A
VH [mV]
± 0.02
-1.71
-1.82
-1.94
-2.07
-2.19
-2.30
-2.43
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
Ic [mA]
± 0.01
3.28
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
0.49
0.53
0.60
0.67
0.75
0.82
0.90
0.97
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
1.04
1.11
1.20
1.26
1.33
1.42
1.49
Ic [mA]
± 0.01
-3.28
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
-0.46
-0.50
-0.57
-0.64
-0.72
-0.80
-0.87
-0.93
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
25
VH [mV]
± 0.02
-1.01
-1.09
-1.15
-1.23
-1.30
-1.38
-1.46
Tabella 1.9: Germanio tipo N: Ib 0.393 ± 0.001 A
Ic [mA]
± 0.01
3.29
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
0.18
0.19
0.23
0.24
0.27
0.30
0.33
0.34
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
0.38
0.40
0.42
0.46
0.48
0.50
0.53
Ic [mA]
± 0.01
-3.28
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
-0.15
-0.16
-0.18
-0.21
-0.24
-0.27
-0.30
-0.32
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
-0.34
-0.37
-0.39
-0.40
-0.44
-0.46
-0.48
Tabella 1.10: Germanio tipo N: Ib 0.097 ± 0.001 A
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
-0.42
-0.45
-0.51
-0.57
-0.63
-0.70
-0.76
-0.82
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
-0.88
-0.94
-1.00
-1.07
-1.12
-1.20
-1.25
Ic [mA]
± 0.01
-3.28
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
0.38
0.41
0.47
0.54
0.59
0.65
0.71
0.78
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
0.84
0.91
0.96
1.02
1.09
1.15
1.20
Tabella 1.11: Germanio tipo N: Ib -0.405 ± 0.001 A
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
0.74
-0.78
-0.90
-1.00
-1.11
-1.22
-1.33
-1.44
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
-1.56
-1.66
-1.77
-1.88
-1.99
-2.10
-2.21
Ic [mA]
± 0.01
-3.30
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
0.70
0.74
0.85
0.96
1.07
1.18
1.29
1.40
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
1.51
1.62
1.74
1.84
1.95
2.06
2.17
Tabella 1.12: Germanio tipo N: Ib -0.700 ± 0.001 A
1.4.3
Risultati
Per ogni serie di dati si è eseguito un fit lineare per ricavare la costante di Hall
RH dalla relazione
RH
IB
VH =
d
Il procedimento seguito per l’interpolazione lineare è analogo a quello utilizzato nella prima parte dell’esperienza, quindi verranno riportati solamente i
26
Effetto Hall nei semiconduttori
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
-1.07
-1.12
-1.28
-1.44
-1.71
-1.76
-1.92
-2.07
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
-2.23
-2.40
-2.55
-2.71
-2.87
-3.04
-3.20
Ic [mA]
± 0.01
-3.30
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
1.02
1.09
1.25
1.40
1.57
1.72
1.88
2.04
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
2.19
2.35
2.51
2.66
2.83
2.98
3.14
Tabella 1.13: Germanio tipo N: Ib -1.000 ± 0.001 A
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
-1.38
-1.46
-1.68
-1.87
-2.08
-2.28
-2.49
-2.70
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
-2.90
-3.10
-3.32
-3.52
-3.72
-3.93
-4.14
Ic [mA]
± 0.01
-3.30
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
1.33
1.41
1.62
1.83
2.02
2.23
2.44
2.64
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
VH [mV]
± 0.02
2.85
3.06
3.26
3.46
3.66
3.87
4.07
Tabella 1.14: Germanio tipo N: Ib -1.299 ± 0.001 A
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
VH [mV]
± 0.02
-1.69
-1.79
-2.05
-2.30
-2.56
-2.81
-3.05
-3.32
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.02
-3.56
-3.82
-4.08
-4.32
-4.57
-4.83
-5.08
Ic [mA]
± 0.01
-3.30
-3.50
-4.00
-4.50
-5.00
-5.50
-6.00
-6.50
VH [mV]
± 0.02
1.66
1.76
2.01
2.27
2.52
2.78
3.02
3.28
Ic [mA]
± 0.01
-7.00
-7.50
-8.00
-8.50
-9.00
-9.50
-10.00
Tabella 1.15: Germanio tipo N: Ib -1.602 ± 0.001 A
risultati ottenuti.
Prima serie di dati, Ib = (1.600 ± 0.001)[A]
ρ = 0.999
a = (0.024 ± 0.004)[mV ]
b = (0.4852 ± 0.0005)[V A−1 ]
χ2 = 0.13
DF = 28 → χ2critico = 1.5
RH =
bd
B
B = (0.327 ± 0.008)[T ]
= (0.00296 ± 0.00008)[m3C −1 ]
VH [mV]
± 0.02
3.53
3.79
4.04
4.29
4.54
4.80
5.05
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
27
VH @mVD
4
2
-10
-5
5
10
IC @mAD
-2
-4
Figura 1.14: Germanio tipo N: prima serie di dati, Ib 1.600 A
VH @mVD
4
2
-10
-5
5
10
IC @mAD
-2
-4
Figura 1.15: Germanio tipo N: seconda serie di dati, Ib 1.300 A
Seconda serie di dati, Ib = (1.300 ± 0.001)[A]
ρ = 0.999
a = (0.011 ± 0.004)[mV ]
b = (0.4209 ± 0.0005)[V A−1 ]
χ2 = 0.15
DF = 28 → χ2critico = 1.5
RH =
bd
B
B = (0.266 ± 0.008)[T ]
= (0.00316 ± 0.00010)[m3C −1 ]
28
Effetto Hall nei semiconduttori
Terza serie di dati, Ib = (1.000 ± 0.001)[A]
VH @mVD
3
2
1
-10
-5
5
10
IC @mAD
-1
-2
-3
Figura 1.16: Germanio tipo N: terza serie di dati, Ib 1.000 A
ρ = 0.999
a = (0.011 ± 0.004)[mV ]
b = (0.3341 ± 0.0005)[V A−1 ]
χ2 = 0.07
DF = 28 → χ2critico = 1.5
RH =
bd
B
B = (0.204 ± 0.008)[T ]
= (0.00327 ± 0.00014)[m3C −1 ]
Quarta serie di dati, Ib = (0.701 ± 0.001)[A]
ρ = 0.999
a = (0.014 ± 0.004)[mV ]
b = (0.2446 ± 0.0005)[V A−1 ]
χ2 = 0.09
DF = 28 → χ2critico = 1.5
RH =
B = (0.143 ± 0.008)[T ]
= (0.0034 ± 0.0002)[m3C −1 ]
bd
B
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
29
VH @mVD
2
1
-10
-5
5
10
IC @mAD
-1
-2
Figura 1.17: Germanio tipo N: quarta serie di dati, Ib 0.701 A
Quinta serie di dati, Ib = (0.393 ± 0.001)[A]
VH @mVD
1.5
1
0.5
-10
-5
5
10
IC @mAD
-0.5
-1
-1.5
Figura 1.18: Germanio tipo N: quinta serie di dati, Ib 0.393 A
ρ = 0.999
a = (0.016 ± 0.004)[mV ]
b = (0.1468 ± 0.0005)[V A−1 ]
χ2 = 0.08
DF = 28 → χ2critico = 1.5
RH
B = (0.080 ± 0.008)[T ]
=
= (0.0036 ± 0.0004)[m3C −1 ]
bd
B
30
Effetto Hall nei semiconduttori
Sesta serie di dati, Ib = (0.097 ± 0.001)[A]
VH @mVD
0.4
0.2
-10
-5
5
10
IC @mAD
-0.2
-0.4
Figura 1.19: Germanio tipo N: sesta serie di dati, Ib 0.097 A
ρ = 0.999
a = (0.018 ± 0.004)[mV ]
b = (0.0509 ± 0.0005)[V A−1 ]
χ2 = 0.11
DF = 28 → χ2critico = 1.5
RH
B = (0.020 ± 0.008)[T ]
3 −1
]
= bd
B = (0.005 ± 0.002)[m C
Settima serie di dati, Ib = (−0.405 ± 0.001)[A]
ρ = −0.999
a = (−0.021 ± 0.004)[mV ]
b = (−0.1229 ± 0.0005)[V A−1 ]
χ2 = 0.06
DF = 28 → χ2critico = 1.5
RH =
B = (−0.083 ± 0.008)[T ]
bd
3 −1
]
B = (0.0030 ± 0.0003)[m C
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
31
VH @mVD
1
0.5
-10
-5
5
10
IC @mAD
-0.5
-1
Figura 1.20: Germanio tipo N: settima serie di dati, Ib -0.405 A
Ottava serie di dati, Ib = (−0.700 ± 0.001)[A]
VH @mVD
2
1
-10
-5
5
10
IC @mAD
-1
-2
Figura 1.21: Germanio tipo N: ottava serie di dati, Ib -0.700 A
ρ = −0.999
a = (−0.020 ± 0.004)[mV ]
b = (−0.2188 ± 0.0005)[V A−1 ]
χ2 = 0.04
DF = 28 → χ2critico = 1.5
RH
B = (−0.144 ± 0.008)[T ]
3 −1
= bd
]
B = (0.0030 ± 0.0002)[m C
32
Effetto Hall nei semiconduttori
Nona serie di dati, Ib = (−1.000 ± 0.001)[A]
VH @mVD
3
2
1
-10
-5
5
10
IC @mAD
-1
-2
-3
Figura 1.22: Germanio tipo N: nona serie di dati, Ib -1.000 A
ρ = −0.999
a = (−0.021 ± 0.004)[mV ]
b = (−0.3165 ± 0.0005)[V A−1 ]
χ2 = 0.09
DF = 28 → χ2critico = 1.5
RH
B = (−0.205 ± 0.008)[T ]
= (0.00309 ± 0.00013)[m3C −1 ]
=
bd
B
Decima serie di dati, Ib = (−1.299 ± 0.001)[A]
ρ = −0.999
a = (−0.027 ± 0.004)[mV ]
b = (−0.4106 ± 0.0005)[V A−1 ]
χ2 = 0.07
DF = 28 → χ2critico = 1.5
RH =
B = (−0.266 ± 0.008)[T ]
= (0.00308 ± 0.00010)[m3C −1 ]
bd
B
1.4 Misura dell’effetto Hall - semiconduttore di tipo N
33
VH @mVD
4
2
-10
-5
5
10
IC @mAD
-2
-4
Figura 1.23: Germanio tipo N: decima serie di dati, Ib -1.299 A
Undicesima serie di dati, Ib = (−1.602 ± 0.001)[A]
VH @mVD
4
2
-10
-5
5
10
IC @mAD
-2
-4
Figura 1.24: Germanio tipo N: undicesima serie di dati, Ib -1.602 A
ρ = −0.999
a = (−0.016 ± 0.004)[mV ]
b = (−0.5069 ± 0.0005)[V A−1 ]
χ2 = 0.07
DF = 28 → χ2critico = 1.5
RH
B = (−0.328 ± 0.008)[T ]
=
= (0.00309 ± 0.00008)[m3C −1 ]
bd
B
34
Effetto Hall nei semiconduttori
Riepilogo e conclusioni
Dopo aver verificato la consistenza dei diversi valori trovati per R H , divisi in
base al segno del campo magnetico, si procede al calcolo di due valori medi
attraverso media pesata:
R+
[m3 C −1 ]
H
0.005
0.0036
0.0034
0.00327
0.00316
0.00296
±
±
±
±
±
±
0.002
0.0004
0.0002
0.00014
0.00010
0.00008
R−
[m3 C −1 ]
H
0.0030
0.0030
0.00309
0.00308
0.00309
±
±
±
±
±
0.0003
0.0002
0.00013
0.00010
0.00008
Tabella 1.16: Germanio tipo N: RH calcolati dai fit lineari
+
< RH
>= 0.00312[m3C −1 ]
−
< RH >= 0.00308[m3C −1 ]
< RH >= 0.0031[m3C −1 ]
RH @VmTAD
0.02
0.01
-0.3
-0.2
-0.1
0.1
0.2
0.3
B @TD
-0.01
-0.02
Figura 1.25: Germanio tipo N: valori del coefficiente di Hall in funzione del
campo
L’errore calcolato attraverso la propagazione risulta insignificante rispetto
al valore del coefficiente (si ottiene un errore relativo dello 0.0001%) e quindi
non viene indicato. Il coefficiente di Hall RH ha segno positivo: questo significa
che, come è noto dalla teoria, i portatori di carica maggioritari nel germanio
(semiconduttore) sono cariche positive.
A questo punto si possono ricavare, per il campione di germanio drogato N,
la concentrazione dei portatori di carica e la loro mobilità:
1.5 Misura dell’effetto Hall - semiconduttore di tipo P
p=
µ=
1.5
1.5.1
RH
ρ
35
1
RH e
= 2 ∗ 1021 [m−3 ]
= 0.16 ± 0.04[m2 (V s)−1 ]
Misura dell’effetto Hall - semiconduttore di
tipo P
Setup sperimentale
La fase di setup sperimentale è analoga a quanto già visto per il germanio di
tipo N: occorre sostituire il campione e rieseguire i cablaggi necessari.
1.5.2
Acquisizione dati
Anche l’acquisizione dei dati avviene con modalità analoghe alla precedente,
tuttavia non sono state eseguite le misure invertendo la corrente circolante nel
campione, in quanto dati considerati superflui.
spessore: d = (2.00 ± 0.01)[mm]
larghezza: A = (8.8 ± 0.1)[mm]
lunghezza: L = (22 ± 1)[mm]
R = (422.9 ± 1.3)[Ω]
ρ = (0.338 ± 0.016)[Ωm]
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib 1.599
VH [mV]
± 0.03
27.53
29.19
33.36
37.56
41.65
45.74
49.95
54.05
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
58.12
62.18
66.27
70.37
74.35
78.39
82.42
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib 1.300
VH [mV]
± 0.03
24.05
25.53
29.13
32.75
36.38
40.10
43.63
47.33
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
50.90
54.50
58.10
61.67
65.19
68.78
72.37
Tabella 1.17: Germanio tipo P
1.5.3
Risultati
Analogamente a quanto fatto con il campione di tipo N si è eseguita un’analisi dei
dati per ricavare il valore del coefficiente di Hall e da esso il numero dei portatori
di carica del materiale e la loro mobilità. In questo caso, poichè non è possibile
supporre l’errore sui dati in ascissa trascurabile rispetto all’errore su quelli in
ordinata (supposizione peraltro necessaria per poter applicare correttamente il
36
Effetto Hall nei semiconduttori
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib 1.000
VH [mV]
± 0.03
19.35
20.55
23.52
26.39
29.32
32.25
35.18
38.11
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
41.03
43.71
46.54
49.48
52.38
55.21
58.10
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib 0.501
VH [mV]
± 0.03
10.65
11.29
12.89
14.51
16.10
17.71
19.31
21.00
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
22.57
24.16
25.75
27.33
28.91
30.52
32.10
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
-38.72
-41.38
-44.09
-46.83
-49.46
-52.10
-54.76
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
-57.23
-61.21
-65.19
-69.20
-73.20
-77.10
-81.03
Tabella 1.18: Germanio tipo P
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib -0.501
VH [mV]
± 0.03
-9.39
-9.92
-11.34
-12.80
-14.20
-15.61
-17.01
-18.42
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
-19.85
-21.23
-22.61
-24.00
-25.39
-26.73
-28.11
Ic [mA]
± 0.01
3.30
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib -1.000
VH [mV]
± 0.03
-18.32
-19.38
-22.17
-24.96
-27.65
-30.48
-33.21
-35.93
Tabella 1.19: Germanio tipo P
Ic [mA]
± 0.01
3.32
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib -1.300
VH [mV]
± 0.03
-22.99
-24.34
-27.75
-31.18
-34.79
-38.18
-41.55
-44.98
± 0.001
Ic [mA]
± 0.01
7.00
7.50
8.00
8.50
9.00
9.50
10.00
VH [mV]
± 0.03
-48.36
-51.81
-55.23
-58.61
-61.93
-65.30
-68.65
Ic [mA]
± 0.01
3.32
3.50
4.00
4.50
5.00
5.50
6.00
6.50
Ib -1.600
VH [mV]
± 0.03
-27.12
-28.65
-32.76
-36.96
-41.04
-45.11
-49.17
-53.23
Tabella 1.20: Germanio tipo P
metodo dei minimi quadrati) è stato necessario ricalcolare l’errore sulle tensioni
VH attraverso il metodo detto dell’errore indotto: si effettua un primo fit dei
dati considerati senza incertezze, per ricavare un valore approssimato b 0 del
coefficiente angolare della retta interpolatrice. Quindi si ricalcola l’errore sulle
y con la formula
σy =
p
σi 2 + (b0 σx )2
1.5 Misura dell’effetto Hall - semiconduttore di tipo P
37
VH @mVD
80
70
60
50
40
30
4
5
6
7
8
9
10
IC @mAD
Figura 1.26: Germanio tipo P: prima serie di dati, Ib 1.599 A
Prima serie di dati, Ib = (1.599 ± 0.001)[A]
ρ = 0.999
a = (0.63 ± 0.07)[mV ]
b = (8.20 ± 0.01)[V A−1 ]
χ2 = 1.6
DF = 13 → χ2critico = 1.7
RH =
B = (0.327 ± 0.008)[T ]
bd
3 −1
]
B = (0.050 ± 0.001)[m C
Seconda serie di dati, Ib = (1.300 ± 0.001)[A]
ρ = 0.999
a = (0.32 ± 0.06)[mV ]
b = (7.215 ± 0.009)[V A−1 ]
χ2 = 0.88
DF = 13 → χ2critico = 1.7
RH =
B = (0.266 ± 0.008)[T ]
bd
3 −1
]
B = (0.054 ± 0.002)[m C
38
Effetto Hall nei semiconduttori
VH @mVD
70
60
50
40
30
4
5
6
7
8
9
10
IC @mAD
Figura 1.27: Germanio tipo P: seconda serie di dati, Ib 1.300 A
VH @mVD
50
40
30
20
4
5
6
7
8
9
10
IC @mAD
Figura 1.28: Germanio tipo P: terza serie di dati, Ib 1.000 A
Terza serie di dati, Ib = (1.000 ± 0.001)[A]
ρ = 0.999
a = (0.43 ± 0.05)[mV ]
b = (5.774 ± 0.008)[V A−1 ]
χ2 = 2.11
DF = 13 → χ2critico = 2.13
(per questo test si considera un livello di significatività dell’1%)
RH
B = (0.204 ± 0.008)[T ]
3 −1
= bd
]
B = (0.056 ± 0.002)[m C
1.5 Misura dell’effetto Hall - semiconduttore di tipo P
39
Quarta serie di dati, Ib = (0.501 ± 0.001)[A]
VH @mVD
30
25
20
15
4
5
6
7
8
9
10
IC @mAD
Figura 1.29: Germanio tipo P: quarta serie di dati, Ib 0.501 A
ρ = 0.999
a = (0.09 ± 0.04)[mV ]
b = (3.205 ± 0.005)[V A−1 ]
χ2 = 0.53
DF = 13 → χ2critico = 1.7
RH
B = (0.102 ± 0.008)[T ]
3 −1
]
= bd
B = (0.063 ± 0.002)[m C
Quinta serie di dati, Ib = (−0.501 ± 0.001)[A]
ρ = 0.999
a = (−0.18 ± 0.03)[mV ]
b = (−2.801 ± 0.005)[V A−1 ]
χ2 = 1.2
DF = 13 → χ2critico = 1.7
B = (−0.103 ± 0.008)[T ]
3 −1
RH = bd
]
B = (0.054 ± 0.004)[m C
40
Effetto Hall nei semiconduttori
VH @mVD
4
-10
5
6
7
8
9
10
IC @mAD
-12.5
-15
-17.5
-20
-22.5
-25
-27.5
Figura 1.30: Germanio tipo P: quinta serie di dati, Ib -0.501 A
Sesta serie di dati, Ib = (−1.000 ± 0.001)[A]
VH @mVD
-20
4
5
6
7
8
9
10
IC @mAD
-25
-30
-35
-40
-45
-50
-55
Figura 1.31: Germanio tipo P: sesta serie di dati, Ib -1.000 A
ρ = 0.999
a = (−0.41 ± 0.05)[mV ]
b = (−5.453 ± 0.008)[V A−1 ]
χ2 = 2.04
DF = 13 → χ2critico = 2.13
(per questo test si considera un livello di significatività dell’1%)
RH
B = (−0.205 ± 0.008)[T ]
3 −1
= bd
]
B = (0.053 ± 0.002)[m C
1.5 Misura dell’effetto Hall - semiconduttore di tipo P
41
Settima serie di dati, Ib = (−1.300 ± 0.001)[A]
VH @mVD
4
5
6
7
8
9
10
IC @mAD
-30
-40
-50
-60
Figura 1.32: Germanio tipo P: settima serie di dati, Ib -1.300 A
ρ = 0.999
a = (−0.54 ± 0.06)[mV ]
b = (−6.826 ± 0.009)[V A−1 ]
χ2 = 1.6
DF = 13 → χ2critico = 1.7
B = (−0.266 ± 0.008)[T ]
3 −1
RH = bd
]
B = (0.051 ± 0.002)[m C
Ottava serie di dati, Ib = (−1.600 ± 0.001)[A]
ρ = 0.999
a = (−0.64 ± 0.07)[mV ]
b = (−8.06 ± 0.01)[V A−1 ]
χ2 = 2.08
DF = 13 → χ2critico = 2.13
(per questo test si considera un livello di significatività dell’1%)
B = (−0.328 ± 0.008)[T ]
3 −1
RH = bd
]
B = (0.049 ± 0.001)[m C
42
Effetto Hall nei semiconduttori
VH @mVD
4
5
7
6
8
9
10
IC @mAD
-30
-40
-50
-60
-70
-80
Figura 1.33: Germanio tipo P: ottava serie di dati, Ib -1.600 A
Riepilogo e conclusioni
Una prima differenza che si può osservare tra questo campione e il precedente
è che in questo caso, siccome le correnti misurate sono più elevate che nel germanio drogato N mentre l’errore associato resta lo stesso, i test di consistenza
e i tests del χ2 sono meno precisi: in alcuni casi è stato necessario scegliere un
livello di significatività dell’1% per poter asserire che la curva calcolata è quella
che interpola la distribuzione dei dati. In nessun caso, comunque, si è dovuto
scartare dei dati o i tests hanno dato esito negativo, quindi si ritiene che l’errore
utilizzato sia corretto e che non ci sia stata una sottostima dell’incertezza delle
misure.
Anche in questo caso, come era prevedibile, il segno di RH è positivo e quindi
i portatori sono cariche positive. Dopo aver verificato la consistenza dei diversi
valori trovati per RH , divisi in base al segno del campo magnetico, si procede
al calcolo del valore medio attraverso media pesata:
R+
[m3 C −1 ]
H
0.063
0.056
0.054
0.050
±
±
±
±
0.002
0.002
0.002
0.001
R−
[m3 C −1 ]
H
0.054
0.053
0.051
0.049
±
±
±
±
0.004
0.002
0.002
0.001
Tabella 1.21: Germanio tipo P: RH calcolati dai fit lineari
+
< RH
>= 0.0529[m3C −1 ]
−
< RH >= 0.0507[m3C −1 ]
< RH >= 0.0517[m3C −1 ]
L’errore calcolato attraverso la propagazione risulta insignificante rispetto al
valore del coefficiente (si ottiene un errore relativo dello 0.0001%) e quindi non
1.6 Misura della resistività di un semiconduttore
43
RH @VmTAD
0.2
0.15
0.1
0.05
-0.3
-0.2
-0.1
0.1
0.2
0.3
B @TD
Figura 1.34: Germanio tipo N: valori del coefficiente di Hall in funzione del
campo
viene indicato.
A questo punto si possono ricavare, per il campione di germanio drogato P,
la concentrazione dei portatori di carica e la loro mobilità, esattamente come
per il campione di germanio drogato N:
p = 1.2 ∗ 1020 [m−3 ]
µ = 0.153 ± 0.007[m2(V s)−1 ]
Si può notare che il numero dei portatori nel campione con drogaggio N
è superiore di circa 20 volte al numero dei portatori nel campione drogato P,
mentre la mobilità degli stessi è confrontabile nei due campioni.
1.6
Misura della resistività di un semiconduttore
A differenza di quanto accade nei conduttori metallici, nei semiconduttori la
resistività ρ non è funzione lineare della temperatura. Infatti nei semiconduttori si verifica un aumento della resistività come conseguenza dell’aumento della
temperatura fino ad una temperatura di inversione: per temperature superiori
si ha una ripida diminuzione della resistività del semiconduttore. Per teorizzare
questo fatto occorre valutare gli effetti della mobilità dei portatori di carica e
del numero degli stessi.
All’aumentare della temperatura consegue un aumento dell’agitazione termica degli atomi che compongono il reticolo del conduttore. Aumentando l’energia cinetica degli atomi, i portatori di carica hanno una maggiore probabilità
44
Effetto Hall nei semiconduttori
di urtare contro il reticolo cristallino, quindi la loro sezione d’urto aumenta e
aumenta quindi la resistività. Questo fenomeno è preponderante nei conduttori
e determina l’andamento lineare della resistività in questo tipo di materiali. La
diminuzione della mobilità segue una legge del tipo
µ = µ0 T −α
con α = 2
Nei semiconduttori intrinseci occorre considerare un altro tipo di fenomeno.
I semiconduttori intrinseci presentano caratteristiche elettroniche tipiche
degli isolanti, ovvero allo stato fondamentale non hanno alcun elettrone in banda di conduzione, mentre i conduttori hanno bande di valenza e conduzione
entrambe popolate. A differenza degli isolanti, i semiconduttori presentano un
gap energetico che separa le bande di conduzione e valenza più piccolo. A conseguenza di questo fatto fornendo energie minori alcuni elettroni di valenza possono andare a popolare la banda di conduzione, permettendo il passaggio di una
piccola corrente di cariche. Per portare alcuni elettroni in banda di conduzione
è sufficiente un aumento di temperatura. Si verifica infatti che aumentando la
temperatura aumenta il numero dei portatori di carica nei semiconduttori (quindi una diminuzione della resistività), mentre questo effetto è trascurabile nei
conduttori ohmici. Si può ragionevolmente supporre che il numero dei portatori
di carica segua una legge esponenziale di temperatura, sfruttando la statistica
di Stefan Boltzman. Quando il termine kT diventa confrontabile con l’energia
di attivazione EA questo fenomeno assume importanza misurabile.
EA
n = Ae− kT
Questi due fenomeni si manifestano contemporaneamente: ne segue che a
basse temperature la resistività cresce all’aumento della temperatura per diminuzione della mobilità dei portatori di carica, mentre ad alte temperature la
resistività diminuisce, in quanto il termine più importante diventa l’aumento dei
carriers. Il punto di inversione avviene normalmente a temperatura ambiente ed
è un parametro dipendente dal semiconduttore considerato (per il Ge è a circa
30◦ C).
1.6.1
Setup sperimentale
In questa fase dell’esperienza occorre valutare la resistività di un campione di
Ge, semiconduttore intrinseco (non drogato), per diversi valori di temperatura.
La resistenza del campione è misurata facendo circolare all’interno dello stesso
una corrente costante e misurando la caduta di tensione ai capi del semiconduttore. La temperatura è misurata mediante una termocoppia con giunzione
ferro-costantana e la misura avviene in un dewar quasi adiabatico al fine di limitare gli scambi termici con l’ambiente e quindi rendere più lente le variazioni
di temperatura.
La misura avviene in un ambiente isolato termicamente dal laboratorio, all’interno di un dewar coibentato, di forma cilindrica, all’interno del quale è posto
1.6 Misura della resistività di un semiconduttore
Alimentazione del riscaldatore
45
Circuito della termocoppia
Norma
A
V
+
Misura di R
+
+
18,0V
out
generatore di
corrente costante
-
bagno di
ghiaccio
giunzione nei
pressi del sensore
Metex
voltmetro ad
alta impedenza
A
V
campione di
germanio
Figura 1.35: Setup sperimentale: misura della resistività di un semiconduttore
il campione. Il campione è posto a contatto con una delle estremità della termocoppia ed è provvisto di una calza di rame per facilitare gli scambi termici
con l’azoto liquido che servirà per il raffreddamento. Nei pressi del campione
è posta una resistenza per il riscaldamento dell’ambiente all’interno del dewar
tramite effetto Joule.
Tutti i collegamenti avvengono tramite boccole poste sul tappo di sughero
che chiude il dewar. Due boccole controllano il riscaldatore che deve essere alimentato con una tensione massima di 25V e una corrente regolabile per fornire
potenze variabili durante la fase di riscaldamento del campione. A causa di
scambi termici con l’esterno, infatti, a energia fissata si raggiunge una temperatura di equilibrio: per superare tale valore occorre aumentare la potenza per
il riscaldamento. Le boccole devono essere collegate ad un regolatore dotato
di potenziometro per la regolazione della potenza in uscita; quest’ultimo deve
essere alimentato con una tensione di 25V ed è provvisto di due terminali per
inserire un amperometro e misurare la potenza immessa nel dewar.
Altre due boccole sono collegate internamente con le estremità della termocoppia ferro-costantana e possono essere collegate direttamente ad un voltmetro
molto sensibile (0.01 mV di sensibilità) per il monitoraggio della temperatura.
La lettura avviene confrontando la misura fornita dal voltmetro con le apposite
tabelle di calibrazione fornite dal costruttore della giunzione. L’altra estremità della termocoppia che fuoriesce dal tappo di sughero deve essere mantenuta
ad una temperatura costante di 0◦ C. Questa condizione può essere realizzata
inserendo la giunzione in un bagno di ghiaccio fondente creato versando azoto
liquido in un bagno di acqua. Al fine di mantenere costante la temperatura
all’interno del bagno occorre mescolare di tanto in tanto il ghiaccio in fusione.
Le altre quattro boccole sono collegate, mediante normali cavi di rame e
46
Effetto Hall nei semiconduttori
saldature a Sn-Pb, alle estremità del semiconduttore. Due servono per fornire
corrente al campione, mentre le altre due per misurare la caduta di tensione ai
capi dello stesso. La corrente di alimentazione deve essere mantenuta costantemente ad un valore di circa 5 mA per tutta la durata dell’esperimento, quindi
è opportuno utilizzare un regolatore di corrente e collegare in serie al campione
un milliamperometro preciso. La caduta di tensione ai capi del campione di
Germanio deve essere misurata con un millivoltmetro ad alta impedenza al fine
di rendere trascurabile l’errore sistematico sulla grandezza valutata introdotto
dallo strumento.
1.6.2
Acquisizione dati
La prima procedura da eseguire è la preparazione di una quantità di ghiaccio
sufficiente per tutta la durata della misura (circa 3 ore). È consigliabile procedere con piccole quantità di acqua, versando di volta in volta l’azoto liquido
e verificando che l’intera massa di acqua sia transita allo stato solido prima di
aggiungerene altra. In questo modo si evita la creazione di uno strato di ghiaccio
solo superficiale che impedirebbe all’acqua sottostante di ghiacciare. Una volta
ottenuta la massa di ghiaccio occorre praticarvi un piccolo foro con l’ausilio di
un cacciavite per introdurvi l’estremità della termocoppia.
Quindi si procede all’inserimento dell’azoto liquido per eseguire la misura
a partire da basse temperature. Quando la temperatura all’interno del dewar
si è stabilizzata è possibile rimuovere l’azoto e misurare le cadute di tensione
ai capi del campione, a corrente costante, e a step di temperatura costanti (di
5◦ C), annotando le coppie T, V corrispondenti. Dopo aver rimosso l’azoto è
necessario richiudere il campione nel dewar in un tempo rapido, infatti la temperatura dello stesso raggiunge in un breve periodo la temperatura ambiente
se viene lasciato all’esterno del recipiente, rendendo illeggibili i corrispondenti
valori di tensione. Si può quindi procedere con un riscaldamento del campione
fornendo tensione alla resistenza. Raggiunta una temperatura di circa 150 ◦ C
è possibile spegnere il riscaldatore e procedere all’esecuzione del ciclo inverso.
Raggiunta nuovamente la temperatura ambiente si può inserire altro azoto liquido per riportare il campione a basse temperature, misurando contestualmente
le tensioni corrispondenti. Occorre sempre verificare e correggere eventuali variazioni della corrente circolante nel campione agendo sulla manopola posta sul
regolatore di corrente.
Si è verificato che sbalzi di temperatura troppo rapidi portano a misure poco
precise, in quanto pur essendo la termocoppia posta a contatto con il campione, a causa delle diverse dimensioni geometriche e composizone presenta una
capacità termica molto diversa. Ne consegue che variazioni troppo rapide di
temperatura portano a variazioni rapide della temperatura della giunzione della
termocoppia, mentre il campione cambia temperatura in modo più graduale.
Ne segue che la temperatura misurata in caso di sbalzi rapidi non corrisponde
effettivamente a quella del campione che determina la variazione di resistività
di quest’ultimo. È quindi sconsigliato aprire il dewar per velocizzare l’acquisizione dei dati o accendere improvvisamente il riscaldatore a elevata potenza.
Ovviamente inserendo l’azoto nel dewar la transizione sarà molto rapida, quindi
1.6 Misura della resistività di un semiconduttore
47
meno precisa rispetto a quella ottenuta nella fase di riscaldamento nello stesso
range di temperature.
Si fornisce al generatore di corrente una tensione costante di 12 V e si fissa
la corrente circolante nel campione a 5 mA.
T [◦ C]
-75
-70
-65
-60
-55
-50
-45
-40
-35
-30
-25
-20
-15
-10
-5
0
VT [mV]
± 0.01
-3.56
-3.34
-3.12
-2.89
-2.66
-2.43
-2.20
-1.96
-1.72
-1.48
-1.24
-0.99
-0.75
-0.50
-0.25
0.00
VGe [mV]
± 0.1
77.0
80.7
84.8
89.1
94.2
99.4
104.6
109.6
116.9
123.5
130.8
138.0
145.6
153.3
161.3
169.3
T [◦ C]
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
Salita
VT [mV]
± 0.01
0.25
0.51
0.76
1.02
1.28
1.54
1.80
2.06
2.32
2.59
2.85
3.12
3.38
3.65
3.92
4.19
VGe [mV]
± 0.1
177.4
185.0
191.5
197.9
203.9
208.1
211.6
212.4
211.6
206.8
192.9
172.9
155.9
132.4
109.4
96.4
T [◦ C]
VT [mV]
± 0.01
VGe [mV]
± 0.1
85
90
95
100
105
110
115
120
125
130
135
140
145
150
4.46
4.73
4.99
5.27
5.54
5.81
6.09
6.36
6.63
6.91
7.18
7.46
7.73
8.00
83.9
69.1
56.8
48.9
42.8
36.2
29.9
24.6
20.6
18.7
16.1
14.5
12.4
10.6
T [◦ C]
VT [mV]
± 0.01
VGe [mV]
± 0.1
Tabella 1.22: Salita
T [◦ C]
150
145
140
135
130
125
120
115
110
105
100
95
90
85
80
75
70
VT [mV]
± 0.01
8.00
7.73
7.46
7.18
6.91
6.63
6.36
6.09
5.81
5.54
5.27
4.99
4.73
4.46
4.19
3.92
3.65
VGe [mV]
± 0.1
10.6
10.9
11.3
12.1
13.3
14.9
16.8
19.4
22.7
26.7
32
38.6
46.6
57.5
70.8
86.6
106.2
T [◦ C]
65
60
55
50
45
40
35
30
25
20
15
10
5
0
-5
-10
-15
Discesa
VT [mV]
± 0.01
3.38
3.12
2.85
2.59
2.32
2.06
1.80
1.54
1.28
1.02
0.76
0.51
0.25
0.00
-0.25
-0.50
-0.75
VGe [mV]
± 0.1
129.3
152.3
174.5
191.2
203.9
211.7
213.8
211.7
207.4
206.5
206.2
205.8
204.9
203
200.8
198.4
194.6
-20
-25
-30
-35
-40
-45
-50
-55
-60
-65
-70
-75
-80
-85
-90
-95
-0.99
-1.24
-1.48
-1.72
-1.96
-2.20
-2.43
-2.66
-2.89
-3.12
-3.34
-3.56
-3.78
-4.00
-4.21
-4.42
192.9
186.9
180.8
173.2
155.4
146.5
138.4
131.2
123.0
113.2
104.5
95.4
86.5
78.7
71.8
64.8
Tabella 1.23: Discesa
T [◦ C]
-70
-65
-60
-55
-50
-45
-40
VT [mV]
± 0.01
-3.34
-3.12
-2.89
-2.66
-2.43
-2.20
-1.96
VGe [mV]
± 0.1
81.5
85.3
89.9
94.9
100.2
105.5
111.3
T [◦ C]
-35
-30
-25
-20
-15
-10
-5
Discesa
VT [mV]
± 0.01
-1.72
-1.48
-1.24
-0.99
-0.75
-0.50
-0.25
VGe [mV]
± 0.1
117.6
123.9
130.6
137.6
145.4
153.2
159
T [◦ C]
0
5
10
15
20
VT [mV]
± 0.01
0.00
0.25
0.51
0.76
1.02
VGe [mV]
± 0.1
164.8
168.4
173.9
179.4
188.2
Tabella 1.24: riSalita
1.6.3
Risultati
Le incertezze riportate nelle tabelle rappresentano la sensibilità degli strumenti
utilizzati. In realtà l’errore da associare alle misure è maggiore della semplice
sensibilità dello strumento ed è dovuto alle modalità di acquisizione dei dati: è
48
Effetto Hall nei semiconduttori
necessario leggere contemporaneamente più tester che non forniscono un risultato preciso ma una cifra che oscilla. Si stima quindi, considerando il tempo di
reazione e l’intervallo entro cui oscillano i valori misurati dal tester, di associare
ai dati i seguenti errori: errore su VT 0.1 mV, errore su VGe 0.5 mV.
Per associare un’incertezza ai valori della temperatura, ricavati da una tabella di conversione T(VT ) fornita in laboratorio, è necessario propagare l’errore
su VT . Poichè la relazione tra T e VT non è nota la si calcola attraverso un’interpolazione con polinomi di grado sempre maggiore. Il test del χ2 permette
quindi di scegliere la migliore approssimazione che è il fit cubico.
T @°CD
150
100
50
-2
2
4
6
8
VT @mVD
-50
Figura 1.36: Relazione T (V ) per la termocoppia
T = (0.028 + 19.9x − 0.24x2 + 0.012x3 )
I dati raccolti vengono dapprima messi in un unico grafico, separando con
colori diversi la salita e la discesa: in grigio scuro è indicata la salita, in grigio
chiaro la discesa. Si può notare che per quanto riguarda i dati ad alte temperature le due curve, in salita e in discesa, sono distanziate di una quantità fissa:
questo perchè la termocoppia si riscalda (e si raffredda) prima del campione e
questo introduce un certo errore sistematico nella misura. Invece per quanto
riguarda i dati a basse temperature l’andamento della curva di discesa è molto
diverso rispetto alle due di salita: si suppone che ciò sia dovuto al fatto che per
tornare indietro è necessario aggiungere azoto liquido per raffreddare il campione e quindi si introduce un errore dovuto alla brusca variazione delle condizioni
ambientali in cui si trova il campione.
Si calcola la resistenza dividendo le tensioni misurate per la corrente (costante,
5 mA).
1.6 Misura della resistività di un semiconduttore
49
VGe @mVD
200
150
100
50
-100
-50
50
100
150
T @°CD
Figura 1.37: Dati raccolti: prima salita, discesa e risalita
R @WD
40
30
20
10
250
300
350
400
T @°KD
Figura 1.38: Prima serie di dati: salita, R(T )
Si studia diversamente l’andamento di R in funzione di T alle basse temperature (regione intrinseca) e alle alte temperature (regione estrinseca).
Regione intrinseca
Ci si attende un andamento del tipo R = R0 T −α , con α = 2, quindi si studia
l’andamento del logaritmo di R in funzione del logaritmo di T. Si dovrà trovare
una retta di coefficiente angolare b eguale ad α. Anche in questo caso l’errore
sulle x non è trascurabile e quindi se ne tiene conto attraverso il metodo dell’er-
50
Effetto Hall nei semiconduttori
R @WD
40
30
20
10
250
300
350
400
T @°KD
Figura 1.39: Seconda serie di dati: discesa, R(T )
R @WD
35
30
25
220
240
260
280
Figura 1.40: Terza serie di dati: risalita, R(T )
rore indotto già illustrato in precedenza.
Prima serie: salita
ρ = 0.998
a = (−8.54 ± 0.18)
b = (2.43 ± 0.03)
χ2 = 1.2
DF = 21 → χ2critico = 1.56
T @°KD
1.6 Misura della resistività di un semiconduttore
51
Log@RD
5.4
5.2
5
4.8
4.6
4.4
5.3
5.4
5.5
5.6
5.7
Log@TD
Figura 1.41: Prima serie: Log(R) in funzione di Log(T ), punti sperimentali e
retta interpolatrice
Seconda serie: discesa
ρ = 0.997
a = (−12.6 ± 0.5)
b = (3.2 ± 0.1)
χ2 = 0.57
DF = 10 → χ2critico = 1.8
Terza serie: risalita
ρ = 0.999
a = (−8.5 ± 0.3)
b = (2.42 ± 0.06)
χ2 = 0.28
DF = 14 → χ2critico = 1.7
Conclusioni
Si confrontano i coefficienti angolari ottenuti con il valore di α atteso, 2. Mentre
per i due tratti in salita la pendenza non è esattamente 2 ma un valore vicino,
il terzo valore, corrispondente al tratto in discesa, è molto più grande (3.2):
questo conferma l’impressione iniziale che i dati nel tratto di discesa fossero
meno attendibili.
52
Effetto Hall nei semiconduttori
Log@RD
5
4.8
4.6
4.4
5.25
5.3
5.4
5.35
5.45
Log@TD
4.2
Figura 1.42: Seconda serie: Log(R) in funzione di Log(T ), punti sperimentali e
retta interpolatrice
Log@RD
5.2
5
4.8
4.6
5.3
5.35
5.4
5.45
5.5
5.55
5.6
5.65
Log@TD
Figura 1.43: Terza serie: Log(R) in funzione di Log(T ), punti sperimentali e
retta interpolatrice
Regione estrinseca
EA
In questo caso l’andamento atteso è del tipo R = R0 e kT quindi si studia l’andamento di Log(R) in funzione di T1 .
1.6 Misura della resistività di un semiconduttore
53
Log@RD
5
4.5
4
3.5
3
0.0023
0.0024
0.0025
0.0026
0.0027
0.0028
0.0029
0.003
1T
Figura 1.44: Prima serie: Log(R) in funzione di 1/T , punti sperimentali e retta
interpolatrice
Prima serie: salita
ρ = 0.999
a = (−8.5 ± 0.2)
b = (4600 ± 90)[K]
χ2 = 0.4
DF = 16 → χ2critico = 1.6
Seconda serie: discesa
ρ = 0.999
a = (−9.2 ± 0.3)
b = (4700 ± 90)[K]
χ2 = 0.5
DF = 15 → χ2critico = 1.7
Conclusioni
Con i risultati dei fit sulle alte temperature si può calcolare la costante EA ,
energia di attivazione, per le due serie di dati (salita e discesa).
EA1 = bkB = (6.38 ± 0.12) ∗ 10−20 [J] = (0.398 ± 0.008)[eV ]
EA2 = bkB = (6.55 ± 0.13) ∗ 10−20 [J] = (0.409 ± 0.008)[eV ]
54
Effetto Hall nei semiconduttori
Log@RD
5.5
5
4.5
4
3.5
3
2.5
0.0024
0.0025
0.0026
0.0027
0.0028
0.0029
0.003
0.0031
1T
Figura 1.45: Seconda serie: Log(R) in funzione di 1/T , punti sperimentali e
retta interpolatrice
Capitolo 2
Rivelazione di raggi cosmici
2.1
Introduzione e fisica dell’esperienza
I raggi cosmici sono costituiti da particelle, quali nuclei ionizzati (90% protoni,
9% particelle alpha), che raggiungono in buona percentuale la superficie terrestre dopo aver attraversato l’atmosfera perdendo parte della loro energia. I
raggi cosmici vengono classificati in base alla loro energia: si tratta di particelle
relativistiche o ultrarelativistiche, con energia comparabile alla loro massa. Al
livello del mare la maggior parte dei raggi cosmici è costituita da muoni (µ± ),
particelle cariche con una bassa sezione d’urto. Una parte dei raggi cosmici
primari, urtando con particelle presenti nell’atmosfera, produce raggi secondari.
La provenienza dei raggi cosmici non è ben nota, tuttavia si sa che essi
provengono dall’esterno del nostro sistema solare, ma dall’interno della galassia.
Lo scopo dell’esperienza è di prendere familiarità con le tecniche di misura
nella fisica delle alte energie, utilizzando rivelatori e contatori per il monitoraggio della quantità di raggi cosmici che giungono sulla superficie terrestre. Inoltre
verrà misurato un parametro importante del rivelatore: l’efficienza.
2.1.1
Raggi cosmici
I raggi cosmici sono particelle che colpiscono la Terra con una frequenza di 180
particelle per cm2 al secondo. Esse sono nuclei ionizzati, circa il 90% di protoni,
9% di particelle α ed il resto di nuclei pesanti e sono distinguibili per le loro alte
energie. Molti raggi cosmici sono relativistici, hanno energie comparabili alla
propria massa o anche maggiori. Pochi di questi hanno energie ultra relativistiche che si estendono sopra i 1020 eV (circa 20 J), undici ordini di grandezza di
differenza con l’energia di massa del protone.
Le domande ancora attuali per quanto riguarda gli studi della fisica dei raggi
cosmici sono la loro provenienza e come possano essere accelerati fino a cosı̀ alte
energie. Sicuro è che provengano dall’esterno dal sistema solare ma dall’interno
della nostra galassia. La piccola parte di particelle relativistiche che ha origine
55
56
Rivelazione di raggi cosmici
nella nostra stella corrisponde a periodi di grande attività solare ed è caratterizzata da una rapida variabilità. Infatti la rivelazione dei raggi cosmici dimostra
una anti correlazione con l’attività solare.
Fino all’avvento degli acceleratori, i raggi cosmici e le loro interazioni erano
l’unico sistema per indagare il mondo delle particelle elementari. Ci sono quindi
molte importanti aree da studiare per meglio comprendere le leggi che governano
le interazioni dei raggi cosmici:
• la produzione di seconda radiazione cosmica, come gli antiprotoni, generata dallo scontro di particelle della radiazione cosmica primaria con nuclei
atomici nel mezzo interstellare, dal cui ammontare si può studiare come
un raggio cosmico si propaga nel mezzo interstellare e come la materia e
i campi di quest’ultimo sono strutturati;
• la produzione di fotoni, neutrini ed altre particelle nelle collisioni dei raggi cosmici con materia vicina alle sorgenti di accelerazione, per capire
l’origine dei raggi e studiare come interagiscono;
• la rivelazione di muoni e neutrini in rivelatori posti in profondità nel
sottosuolo per restringere lo studio alla sola radiazione secondaria;
• la ricerca di particelle esotiche e di nuove interazioni nella radiazione
cosmica.
Questi punti hanno un grande obiettivo in comune: le stesse leggi che governano la cascata di particelle nell’atmosfera terrestre descrivono anche la produzione di particelle dovuta ai raggi cosmici accelerati da collassi stellari.
Il dato principale sui raggi cosmici, dal quale si spera di ottenere qualche informazione riguardo la loro origine, è la relativa abbondanza di differenti nuclei
atomici e la distribuzione di energia di ogni componente. Comparazioni con vari
oggetti come il Sole, il mezzo interstellare, le supernovae o le stelle di neutroni,
possono dare informazioni sul luogo dove i raggi cosmici sono stati accelerati.
Inoltre lo studio delle proprietà dei raggi cosmici (composizione chimica, spettro
energetico, distribuzione delle direzioni d’arrivo) è di importanza fondamentale
per comprendere i meccanismi della loro formazione e propagazione nello spazio
interstellare e intergalattico.
La radiazione cosmica è costituita da nuclei di diversi elementi, con una
piccola frazione di elettroni, di raggi gamma e di neutrini. I nuclei formano la
cosiddetta radiazione cosmica primaria. Dal punto di vista energetico i raggi
cosmici rappresentano una componente fondamentale dell’universo: difatti la
loro densità di energia è approssimativamente di 1 eV /cm3 , confrontabile per
esempio con la densità di energia della luce stellare, 0.6 eV /cm3 , o con quella
del campo magnetico galattico, 0.2 eV /cm3 . La potenza emessa nella galassia
sotto forma di raggi cosmici viene confrontata con quella emessa mediante radiazioni elettromagnetiche.
Attualmente si ritiene che i raggi cosmici siano creati ed accelerati da oggetti
attivi. Possibili sorgenti all’interno della nostra Galassia sono le esplosioni di supernovae, le pulsar e il nucleo galattico stesso. Sorgenti extragalattiche possono
2.1 Introduzione e fisica dell’esperienza
57
essere radio-galassie e quasar, i cui nuclei manifestano un’elevata potenza di
emissione sotto forma di radiazione e di particelle di alta energia, nonché stelle
a neutroni e buchi neri. Devono poi esistere meccanismi che accelerano i raggi
cosmici fino a far loro raggiungere le altissime energie a cui vengono osservati. Il
primo meccanismo fu proposto da Fermi, secondo il quale essi vengono accelerati
dagli urti con nuvole di polvere magnetizzata presenti nella Galassia. Un modello di accelerazione diretta suppone invece che tali particelle siano accelerate da
campi magnetici rotanti molto intensi (come quelli intorno alle stelle a neutroni
o ai dischi di accrescimento dei buchi neri). Altri modelli infine suppongono
che i raggi cosmici di piu’ alta energia siano il prodotto del decadimento di particelle esotiche supermassive (come uno stato legato monopolo-antimonopolo o
stringhe cosmiche superconduttrici).
I raggi cosmici si propagano nello spazio interstellare e intergalattico, interagendo con la polvere, il gas interstellare, i campi magnetici galattici e, sopra
una certa energia, con la radiazione fossile a 2.7 K. Queste interazioni possono
modificarne la composizione chimica, per esempio frammentando i nuclei più
pesanti in altri più leggeri. La presenza del ginocchio potrebbe avere più cause:
potrebbe essere dovuto ad un taglio in energia nei meccanismi di produzione e di
accelerazione, oppure potrebbe essere legato alla propagazione della radiazione
cosmica nello spazio. Alle basse energie (da uno a pochi GeV per nucleone)
l’abbondanza relativa degli elementi chimici nei raggi cosmici è globalmente
molto simile a quella nella materia del Sistema solare, tuttavia alcune differenze
sono significative. Nella radiazione cosmica da un lato vi è una certa scarsità
di idrogeno ed elio, dall’altro vi è un netto eccesso di litio, berillio e boro. La
concentrazione di ferro poi si accorda bene con quella del Sistema solare, ma
c’è una sovrabbondanza degli elementi immediatamente precedenti nella tavola
periodica. Per spiegare questo comportamento si pensa che taluni nuclei, detti primordiali (quali H, He, C, O, Mg, Si, Fe), abbiano alla sorgente la stessa
abbondanza riscontrata nell’universo. Propagandosi nello spazio interstellare,
nel quale possono rimanere anche 106 ÷ 108 anni, essi interagirebbero con la
materia ivi presente e darebbero luogo, con un processo detto di spallazione,
agli elementi più leggeri e quindi più abbondanti (nuclei detti secondari): Li, Be
e B proverrebbero dalla frammentazione di C e O, i nuclei piu’ pesanti (Z > 20)
da quella del ferro. Una misura diretta dei raggi cosmici è possibile solo per
energie fino a 1013 ÷ 1014 eV (10 ÷ 100 TeV), in quanto ad energie superiori il
flusso di particelle è troppo basso e non consente di raccogliere una statistica
sufficiente. Pertanto al di sopra di 1014 eV sono possibili solo misure indirette,
ovviamente meno precise e soprattutto fortemente dipendenti dai modelli di interazione scelti. Generalmente la misura diretta è effettuata con palloni-sonda
che raggiungono gli strati più alti dell’atmosfera; essi possono contenere sia rivelatori passivi (di solito emulsioni fotografiche, ma anche film per raggi X e
plastiche) sia rivelatori attivi (come calorimetri e contatori Cherenkov). Queste
sonde però possono rimanere in atmosfera per poco tempo (dell’ordine di un
giorno), e possono trasportare solo rivelatori di volume ridotto.
Estrapolando i dati delle misure dirette si possono ottenere dei modelli di
composizione. Un flusso continuo di raggi cosmici raggiunge la nostra atmosfera
da tutte le direzioni dello spazio: qui le particelle si moltiplicano in una cascata
di interazioni successive, creando un’invisibile e innocua pioggia cosmica che
58
Rivelazione di raggi cosmici
colpisce continuamente ciascuno di noi alla frequenza di circa 4000 particelle
cariche al minuto. Queste, urtando le particelle dell’atmosfera, le spezzano in
altre piu’ piccole, dette muoni e pioni, che possono essere rivelati sulla superficie
terrestre. Lo studio dei raggi cosmici ci permette di indagare il cosmo attraverso
segnali di alta energia, di studiare la fisica fondamentale ad energie irraggiungibili negli acceleratori qui sulla Terra, e di ottenere preziose indicazioni sulle
prime fasi di evoluzione dell’Universo.
P
collisioni nucleari
n
P
Π+
Π0
anti
materia
Π−
decadimenti
γ
collisioni
nucleari
P
Π0
Π+
γ
produzione di
coppie e+ eΠ−
µ+
ν
µ−
ν
Figura 2.1: Possibili decadimenti di un raggio cosmico
2.1.2
Scintillatori
Gli scinitillatori sono uno dei device più utilizzati per il rilevamento di particelle e nuclei nella fisica moderna. Il loro funzionamento si basa sulla proprietà
di alcuni materiali di emettere un piccolo flash di luce (una scintilla) quando
vengono colpiti da particelle nucleari o da radiazione. Se vengono accoppiati a
fotomoltiplicatori, i quali convertono il segnale luminoso in segnale elettrico e lo
amplificano, è possibile eseguire un preciso conteggio della radiazione incidente
la superficie dello scintillatore.
Il primo esempio di rivelatore di particelle a scintillazione fu costruito da
Crookes nel 1903: esso era composto da uno schermo di ZnS che produceva
piccole scintille quando colpito da particelle α. Le scintille potevano essere viste
con l’ausilio di un microscopio ottico in una camera oscura. Questo strumento
fu molto utile anche nell’esperienza di Geiger e Marsden, tuttavia non fu di
utilizzo comune sino al 1944, quando Curran e Baker lo impiegarono collegato
otticamente ad un fotomoltiplicatore. L’efficienza e la facilità di eseguire misure
con gli scintillatori erano ora paragonabili a quelle dei rivelatori a gas ionizzanti. Lo sviluppo successivo ha riguardato la ricerca di nuovi materiali e soluzioni
2.1 Introduzione e fisica dell’esperienza
59
tecniche per aumentare l’efficienza dell’apparato rivelatore (scintillatore e fototubo).
Lo schema generale di un rivelatore consiste in uno scintillatore accoppiato
con un fotomoltiplicatore, direttamente o mediante una guida d’onda, entrambi
racchiusi da un guscio metallico al fine di eliminare possibili campi magnetici esterni. Le particelle, attraversando il rivelatore, ne eccitano gli atomi o le
molecole; gli atomi eccitati si diseccitano spontaneamente in istanti successivi
emettendo in questa fase il flash di luce. Un sottile strato di Mylar esterno
allo scintillatore che funge da specchio permette ai raggi luminosi emessi in
qualunque direzione di venire riflessi all’ingresso del fotomoltiplicatore con una
buona efficienza. Il fotomoltiplicatore ha il compito di convertire questi flash
in segnali elettrici e di amplificarne l’ampiezza in modo tale che possano essere
misurati e conteggiati.
Gli scintillatori funzionano in base al meccanismo della luminescenza: quando
HighVoltage
Scintillatore
Fotomoltiplicatore
Area sensibile
Mylar riflettente e
strato µ-shield
Guida d'onda
out
Figura 2.2: Schema di uno scintillatore
un oggetto assorbe energia, gli atomi che lo compongono si eccitano (se l’energia
è sufficiente). Dopo un tempo di decadimento, dipendente dalla composizione
chimica del materiale, essi si diseccitano emettendo fotoni di frequenza proporzionale alla differenza di energia tra lo stato eccitato e lo stato diseccitato
(spesso lo stato fondamentale).
∆E = hν
Se la differenza di energia è tale per cui l’emissione avviene nelle frequenze
del visibile si può parlare di fluorescenza (se il tempo di decadimento è dell’ordine delle velocità di transizione atomica - 10−8 s) o di fosforescenza (se il tempo
di decadimento è più lungo - da pochi µs a ore).
In generale si può pensare di descrivere il numero di fotoni N emessi al tempo
t, data un emissione totale N0 e un tempo di transizione τd con la seguente
60
Rivelazione di raggi cosmici
equazione:
N (t) =
N0 e−f ractτd
τd
N (t) = Ae
− τt
f
sistema ad un solo componente
t
+ BAe− τs
sistema a due componenti
Se il sistema ha più componenti uno dei due ha un decadimento più rapido
(fast indice f ) e l’altro decade con un certo ritardo (slow indice s). Questa
caratteristica è sfruttata nella pulse-shape discrimination.
Un buon scintillatore deve presentare un valore elevato di efficienza di conversione, definita come il rapporto tra le particelle che giungono sulla superficie
e quelle che vengono effettivamente rivelate (a causa delle quali viene emessa la
scintilla). A seconda dello scopo per cui è costruito lo scintillatore avrà efficienza
massima nella rivelazione di particelle dotate di una ben precisa energia. Tale
parametro è dipendente dal materiale utilizzato nella costruzione. L’efficienza
viene spesso valutata considendo l’intero sistema scintillatore e fotomoltiplicatore, ovvero definendola come il rapporto tra particelle che urtano il rivelatore
e il numero di impulsi misurato.
Altre caratteristiche tipiche di uno scintillatore sono:
• sensibilità in funzione dell’energia delle particelle incidenti. Al di sopra di
un valore di energia minimo lo scintillatore opera in modo lineare, ovvero
l’intensità del flash generato è proporzionale all’energia della particella
che lo ha colpito. Si verifica che in condizioni normali di lavoro anche
il fotomoltiplicatore opera in modo lineare, quindi l’ampiezza del segnale
di uscita è proporzionale all’energia delle particelle incidenti. Tuttavia i
due device del rivelatore devono essere il più possibile accoppiati, ovvero
lo scintillatore deve emettere radiazione elettromagnetica con lunghezza
d’onda λ interna alla finestra di sensibilità del fototubo;
• tempo di risposta (τ deve essere molto piccolo). Una caratteristica degli
scintillatori è il tempo molto rapido di risposta, cosı̀ come è breve il tempo
necessario affinché il rivelatore ritorni sensibile dopo aver misurato un
evento. Questo fa si che gli scintillatori possano essere utilizzati anche
valutando il numero di particelle in funzione del tempo di esposizione e
che sia possibile discriminare con una risoluzione migliore la separazione
temporale di più eventi distinti. Il rate misurabile con gli scintillatori è
maggiore rispetto a quello misurabile con altri tipi di rivelatori;
• discriminazione della forma degli impulsi. Con alcuni scintillatori è possibile, analizzando la forma dell’impulso in uscita in funzione della frequenza, risalire al tipo di particella rilevata. Questa tecnica è nota come pulseshape discrimination ed è dovuta a differenti meccanismi di fluorescenza
legati a differenti energie ionizzanti;
• trasparenza. La particella deve poter attraversare il rivelatore per poter
eseguire verifiche con altri scintillatori posti in cascata. In questo modo si
hanno misure più precise e il sistema presenta una migliore efficienza;
2.1 Introduzione e fisica dell’esperienza
61
• potenza in uscita. La potenza emessa è un parametro che determina in modo drammatico l’efficienza complessiva, in quanto emissioni deboli spesso
non sono sufficienti per essere rilevate dal fototubo, quindi vengono perduti
i conteggi di tali particelle;
• linearità. Spesso si verifica una relazione di linearità tra energia della
particella incidente e intensità del flash prodotto solo in una piccola sezione
della curva di energia. È quindi importante selezionare correttamente il
tipo di scintillatore in funzione delle particelle che si volgliono studiare.
In generale è utile studiare la curva di risposta del sistema composto da
rivelatore e fototubo al fine di costruire una corretta curva di calibrazione
dell’apparato;
• attenuazione del fascio luminoso. Il fascio emesso dallo scintillatore compie
percorsi diversi e spesso viene riflesso più volte dallo specchio di Mylar
prima che giunga al fotomoltiplicatore. Per garantire una buona linearità
dell’apparato è necessario che il coefficiente di estinzione del materiale di
cui è composto lo scintillatore sia basso e ottimizzato per la frequenza di
emissione dello stesso (in genere questo valore è circa σ = 0.25m−1 ).
Scintillatori organici
Gli scintillatori organici sono costituiti da molecole di idrocarburi aromatici contenenti anelli di benzene. La loro caratteristica principale è la risposta molto
rapida, dell’ordine di pochi nanosecondi o meno.
La scintilla ha origine in questo caso dagli elettroni di valenza liberi delle
molecole: si tratta di elettroni delocalizzati che occupano gli orbitali molecolari
π. Osservando il diagramma dei livelli energetici si nota che le transizioni possono avvenire tra livelli diversi e tra livelli vibrazionali diversi. Le differenze di
energia tra i diversi livelli sono dell’ordine delle decine di eV, mentre l’ampiezza
di ciascuna banda che contiene più livelli vibrazionali è dell’ordine degli eV. La
fluorescenza avviene solo per particolari transizioni energetiche, in altre transizioni il decadimento avviene senza emissione di fotoni. In particolare se il
sistema si trova in uno stato metastabile, prima di poter eseguire una transizione che dia origine a fotoni deve decadere in un livello stabile. Transizioni
tra diversi stati vibrazionali del medesimo livello energetico danno origine a fotoni (responsabili della vibrazione della particella).
A causa della loro struttura molecolare, gli scintillatori organici possono
essere realizzati in diverse forme (cristalli puri, miscele di uno o più componenti
solide o liquide).
• Cristalli organici: i più comuni sono l’antracene (C14 H10 ), il trans-stilbene
(C14 H12 ) e il naftalene (C10 H8 ). Sono caratterizzati da tempi di risposta
molto brevi, dell’ordine di pochi nanosecondi (ad eccezione dell’antracene
- 30 ns). La loro risposta tuttavia non è lineare: a causa della loro costituzione hanno assi di simmetria intrinseci, dovuti alla conformazione del
solido cristallino, quindi sono maggiormente sensibili a particolari direzioni
del fascio incidente. Ne segue che un utilizzo appropriato deve prevedere
un collimatore del fascio di particelle incidenti. L’antracene ha la migliore
62
Rivelazione di raggi cosmici
T2
S2
decadimento T1
interno
S1
assorbimento
fluorescenza
T0
S0
Stati di tripletto
Stati di singoletto
Figura 2.3: Decadimento di elettroni e fluorescenza in una molecola organica
risposta in potenza rispetto a tutti gli altri scintillatori organici: è quindi
utilizzato come unità di confronto, e la potenza emessa da uno scintillatore
viene espressa come percentuale della luce dell’antracene.
• Liquidi organici: sono soluzione di uno o più composti organici (P BD 2 ,
P P O3 o P OP OP 4 ) in solvente organico (xilene, toluene, benzene). In
questo caso sebbene l’emissione di luce venga svolta dal soluto, l’energia derivante dal passaggio di particelle viene assorbita dal solvente e poi
trasferita al soluto con tempi di risposta molto rapidi e buona efficienza.
L’efficienza di conversione varia con la concentrazione, tuttavia si giunge
ad un punto di saturazione oltre il quale non è conveniente aggiungere altro soluto. Normalmente la concentrazione è di qualche grammo di soluto
per litro di solvente. La risposta di questi devices è dell’ordine di 3, 4 ns
ed essi hanno una buona trasparenza, quindi possono essere sovrapposti al
fine di aumentare l’efficienza complessiva dell’apparato di misura. Inoltre
possono essere disciolti nella soluzione altri composti che hanno il compito
di eseguire uno shift in frequenza della luce emessa dal soluto scintillatore.
In questo modo è possibile accordare in frequenza scintillatore e fotomoltiplicatore. Questi scintillatori sono tuttavia molto sensibili alle impurità,
in particolare è stato evidenziato come la presenza di ossigeno in soluzione
porti a un decadimento dell’efficienza della conversione importante.
• Plastici: si tratta di sostanze scintillanti organiche (PBD, PBO) disciolte
in solventi plastici quali poliviniltoluene, polifenilbenzene o polistirene.
Spesso anche in questo caso si aggiungono sostanze per variare la composizione spettrale della risposta all’attraversamento di particelle. I rivelatori
plastici hanno una risposta molto rapida ed emettono una buona potenza.
A causa del tempo di decadimento molto rapido il tempo di eccitazione
non può essere trascurato, quindi la risposta dello scintillatore plastico
sarà allargata (di forma gaussiana). Uno dei maggiori vantaggi di questo
2.1 Introduzione e fisica dell’esperienza
63
tipo di device è la flessibilità, la possibilità di costruire forme diverse, dai
film ai blocchi. Inoltre è possibile ottimizzare il solvente al fine di controllare la velocità della luce nel mezzo e quindi i ritardi di misura. I rivelatori
plastici sono materiali sensibili agli attacchi di solventi organici e vanno
maneggiati con guanti al fine di evitare che gli acidi contenuti nella pelle
possano intaccarne la struttura.
Scintillatori inorganici
Gli scintillatori inorganici sono per la maggior parte cristalli di alcali contenenti
impurità che svolgono azione catalitica. Il materiale più comunemente impiegato è N aI(T l) dove il Tallio costituisce l’attivatore. In generale la risposta di
questi rivelatori è di due o tre ordini di grandezza inferiore in potenza rispetto alla risposta degli scintillatori organici a causa di fenomeni di fosforescenza.
L’eccezione è rappresentata da scintillatori a base di CsF , con tempi di risposta
di 5 ns.
Un problema che limita l’applicazione degli scintillatori inorganici è causato
dalla sensibilità all’umidità, in quanto molti di questi sono cristalli igroscopici
che devono essere protetti e mantenuti in ambiente privo di umidità.
Una delle caratteristiche di questo tipo di scintillatori è l’elevato potere di
fermare le particelle incidenti, dovuto alla elevata densità e alla dimensione degli
atomi che compongono il reticolo. Sono quindi adatti per la rilevazione di raggi
γ e di elettroni o positroni ad alta energia. Tuttavia nel caso si vogliano sovrapporre più rivelatori di tipo diverso è necessario che gli scintillatori inorganici
siano posti per ultimi, in quanto potrebbero fungere da schermo per particelle
di minore energia.
Il meccanismo di eccitazione e diseccitazione avviene a livello atomico, mentre negli scintillatori organici avviene a livello molecolare. Quando una particella
nucleare collide sul cristallo uno o più elettroni passano dalla banda di valenza
alla banda di conduzione creando uno ione (buca) e un elettrone libero. Un
processo alternativo è la creazione di un eccitone, ovvero l’elettrone viene eccitato in una banda appena al di sotto della banda di conduzione: in tal caso
buca ed elettrone restano uniti, ma possono muoversi all’interno del cristallo. Se
all’interno di quest’ultimo sono presenti impurità queste possono essere ionizzate da una coppia elettrone-lacuna. Un elettrone, che raggiunga una lacuna, si
può diseccitare raggiugendo cosı̀ lo stato fondamentale, emettendo nello spettro
esteso del visibile (comprese le regioni dell’ultravioletto e dell’infrarosso). La
transizione può tuttavia avvenire anche senza che venga riemessa radiazione,
con perdita di energia tramite altri tipi di processo.
Scintillatori a gas ionizzazione
Sono costituiti principalmente da gas nobili (Xeno, Krypton, Argo, Elio) o da
miscele di essi ad alta pressione (200 atm circa): in questi sistemi l’eccitazione
avviene a livello del singolo atomo, quindi le transizioni sono molto rapide (entro
1 ns), tuttavia l’emissione avviene generalmente nella regione dell’ultravioletto,
dove i fotomoltiplicatori sono poco efficienti. Al fine di migliorare l’efficienza
64
Rivelazione di raggi cosmici
complessiva dell’apparato si fodera la superficie dello scintillatore con uno strato
di difenistilbene che assorbe la luce nella regione dell’ultravioletto e riemette
nella regione del blu-verde, dove i fototubi sono pis̆ensibili.
2.1.3
Fotomoltiplicatori
I fotomoltiplicatori sono tubi elettronici per convertire segnali luminosi in segnali elettrici. Vengono utilizzati nella fisica delle alte energie in associazione
con scintillatori per convertire il segnale proveniente dal sensore di particelle in
segnale elettrico più maneggevole e facilmente acquisibile da hardware per computer. In questa applicazione il fotomoltiplicatore o fototubo è direttamente
applicato allo scintillatore.
Un fotomoltiplicatore è costituito da un catodo di materiale fotosensibile,
un sistema per la raccolta e la focalizzazione degli elettroni, una stringa di
moltiplicatori (dinodi) e un anodo da cui può essere estratto il segnale. Tutti
i componenti sono inseriti in un tubo a vuoto e l’intero sistema è isolato dalla
luce proveniente dall’esterno, ad eccezione della parte adiacente al catodo che
deve raccogliere i fotoni da convertire.
out
HV
Figura 2.4: Sezione di un fotomoltiplicatore
Il funzionamento del fotomoltiplicatore si basa sull’effetto fotoelettrico. I
materiali metallici, quando investiti da una radiazione elettromagnetica di frequenza opportuna, possono emettere seguendo una legge di probabilità nota
uno o più elettroni. La luce incidente fornisce al metallo un’energia E = hν: se
tale energia è maggiore del lavoro di estrazione del metallo, un elettrone passerà
dalla banda di valenza alla banda di conduzione, diventando elettrone libero
(slegato dal nucleo) e con energia cinetica
Ek = hν − Westrazione
Se tuttavia la frequenza incidente non è sufficiente a far eccitare l’elettrone e a
fare raggiungere allo stesso uno stato slegato il materiale non emetterà elettroni.
L’elettrone che è stato estratto per effetto fotoelettrico dal catodo, viene
collimato da un apposito sistema nella cavità del fototubo e accelerato dalla
differenza di potenziale applicata tra anodo e catodo dello stesso.
2.1 Introduzione e fisica dell’esperienza
65
All’interno del fototubo è presente una serie di dinodi in cascata, anch’essi
di materiale metallico. Essi svolgono la funzione di aumentare il numero di elettroni che si sviluppano in seguito all’arrivo di un treno di fotoni al catodo. Il
loro funzionamento si basa sul fatto che l’urto di un elettrone accelerato contro
una struttura metallica può strappare dalla stessa più elettroni e quindi si ha
un effetto cascata e il numero di elettroni aumenta ad ogni interazione con il
dinodo successivo. In questo modo all’anodo giunge un segnale amplificato che
può essere acquisito mediante contatori dotati di sufficiente sensibilità.
Si assume che il comportamento del fotomoltiplicatore sia di tipo lineare,
ovvero che il segnale presente all’anodo sia proporzionale al numero di fotoni
che eccitano il catodo.
Al fine di ridurre l’assorbimento della radiazione incidente da parte delle
pareti del tubo, la finestra in corrispondenza del catodo è costituita da un cristallo di quarzo opportunamente orientato.
Si definisce l’efficienza del fototubo come
η(λ) =
# di fotoelettroni raccolti all’anodo
# di fotoni incidenti sul catodo
Tale efficienza stima la capacità del rivelatore di rivelare tutti i fotoni incidenti e la dipendenza dalla lunghezza d’onda incidente è legata al fatto che il
materiale fotosensibile ha un determinato lavoro di estrazione e che tale valore
varia a seconda del materiale scelto per la costruzione del rivelatore. È quindi
importante accordare la curva di sensibilità del fotomoltiplicatore con la curva
di emissione dello scintillatore cui verrà collegato otticamente al fine di ottimizzare la catena di rilevamento ed ottenere un’efficienza complessiva ottimale.
Una definizione di efficienza alternativa considera l’intensità luminosa incidente e la potenza emessa dall’anodo
I
e
E(λ) = catodo = η(λ)λ
P (λ)
hc
La maggior parte dei fotocatodi oggi è costituita da materiali semiconduttori (antimonio drogato con uno o più metalli alcalini) che raggiungono efficienze
dell’ordine del 10-30%, mentre i fotocatodi di tipo metallico hanno efficienze dell’ordine dello 0.1%, in quanto all’interno di questi ultimi gli elettroni liberi hanno
una sezione d’urto pi`ù elevata (vi sono numerosi elettroni di conduzione con
cui urtare, mentre ve ne sono meno nel reticolo cristallino di un semiconduttore).
Dopo che l’elettrone viene emesso dal fotocatodo viene collimato da un sistema ottico-elettronico mediante uno o più stadi impieganti magneti o elettromagneti in modo tale che l’elettrone venga deflesso. Le caratteristiche principali che
deve avere un buon collimatore sono l’efficienza (il maggior numero di elettroni
emessi deve raggiungere il primo dinodo), la coerenza temporale (due elettroni
emessi da porzioni diverse del catodo devono raggiungere in tempi confrontabili
il primo dinodo) e velocità di collimazione (utile nel caso debbano essere svolte
misure di tempo su eventi diversi).
66
Rivelazione di raggi cosmici
La sezione di moltiplicatori è caratterizzata dal numero dei dinodi e dal fattore di emissione secondaria δ. L’emissione di elettroni avviene con modalità
anloghe all’effetto fotoelettrico, tuttavia il treno di fotoni è sostituito da uno
o più elettroni. Inoltre deve essere mantenuta una differenza di potenziale tra
i diversi dinodi per accelerare e giudare gli elettoni, quindi deve essere depositato uno strato conduttore su ciascuno di essi. I dinodi possono essere quindi
costituiti da materiali diversi, conduttori, semiconduttori o isolanti, tuttavia si
deposita su ciascuno di essi uno stato di terre rare o metalli alcalini mescolati
con metalli nobili per assicurare la conduzione.
Questo stadio deve assicurare un buon coefficiente di emissione secondaria,
una buona stabilità termica e un debole effetto termoionico al fine di ridurre il
rumore di fondo del convertitore.
In genere il fototubo è costituito da una serie di 10-14 dinodi e può offire un
guadagno di circa 107 volte. La forma e la disposizione dei dinodi può essere
ottimizzata al fine di migliorare le caratteristiche di linearità, guadagno o di
prontezza del fototubo.
Teoricamente un fototubo dovrebbe fornire una risposta costante per elettroni aventi la stessa energia, tuttavia si può osservare un allargamento della
curva di uscita duvuto a fluttuazioni statistiche. Tale allargamento segue una
legge statistica binomiale di Poisson.
Occorre ricordare che nonostante l’isolamento da fonti di luce, al di fuori
della finestra in corrispondenza del catodo si ha un rumore di fondo tipico del
convertitore dovuto a effetti termoionici e fotoelettrici (non attribuibili ai fotoni
incidenti) sul catodo o sui dinodi. Tale rumore comporta errori sistematici sulla risposta in uscita e questa componente deve essere tenuta in considerazione
durante il post-processing dei dati sperimentali.
Si verifica che il coefficiente di emissione secondaria è legato con legge di
proporzionalità diretta alla differenza di potenziale applicata al fototubo
δ = KVd
Considerando n dinodi il guadagno del fotomoltiplicatore può quindi essere
espresso come
G = δ n = (KVd )n
È quindi importante fornire al fotomoltiplicatore la maggiore tensione possibile. Tuttavia oltre un certo limite di tensione applicata il guadagno si stabilizza
a un valore massimo (fotomoltiplicatore saturo) e non aumenta, mentre aumenta
considerevolmente il rumore di fondo (a causa del riscaldamento del fototubo).
La configurazione ottimale prevede una tensione di alimentazione molto stabile,
e regolata ad un valore leggermente inferiore al valore di soglia.
Per fornire a ciascun dinodo la tensione ottimale si impiegano catene di resistenze collegate in serie a ciascun fotodinodo. Lavorando in regime impulsato
sono necessari anche condensatori per compensare i picchi di tensione derivanti
dall’urto di elettroni sul dinodo. In alternativa è possibile sostituire le resistenze
2.1 Introduzione e fisica dell’esperienza
67
con opportuni diodi Zener che mantengono la tensione di poco superiore alla
soglia, ai capi di ciascun dinodo. I migliori risultati si ottengono combinando le
diverse soluzioni, ovvero utilizzando resistenze per i primi stadi e condensatori
e diodi Zener per gli ultimi dinodi.
out
+HV
gnd
out
-HV
gnd
Figura 2.5: Schema elettrico del voltage divider
L’uscita di un fotomoltiplicatore può essere considerata un generatore di
corrente impulsata per costruzione. La capacità e l’impedenza intrinseca del
convertitore devono essere quindi prese in esame per capire come il segnale si
presenta. Possiamo considerare l’intero fotomoltiplicatore come un generatore di corrente con una resistenza e un condensatore collegati in parallelo. La
costante τ = RC è la costante di tempo del sensore ed è legata alla catena di
resistenze e condensatori, oltre che all’impedenza caratteristica di cavi e dinodi.
In uscita la corrente misurata sarà del tipo
I(t) =
V
dV
GN −t
e τs =
+C
τs
R
dt
dove N è il numero di elettroni emessi dal fotocatodo e τs il tempo di diseccitazione dello stesso.
Integrando si ottiene il seguente valore di tensione

i
h
 − GN eR e− τts − e− τt
τ=
6 τs
τ −τs
V (t) =
 − GN2eR te− τts
τ = τs
τ
s
Per τ τs il segnale in uscita è piccolo, tuttavia riproduce fedelmente la curva del segnale prodotto dal fotocatodo. In questo caso si parla di operazione in
corrente e il tempo di risposta è rapido e determinato in buona approssimazione
da τ . Viceversa per τ τs si parla di operazioni in voltaggio e la corrente
68
Rivelazione di raggi cosmici
è integrata dal condensatore. In generale è preferibile lavorare in tensione, in
quanto il segnale è più largo e le fluttuazioni sono soppresse dall’integrazione,
tuttavia il rate dei conteggi deve essere minore dell’inverso di τ per evitare la
sovrapposizione di più segnali. Operando in corrente all’opposto la sensibilità
diminuisce, ma aumenta il rate di conteggi misurabile (aumentano anche le fluttuazioni).
Principali fonti di rumore possono essere derivanti da fluttuazioni statistiche
dei tempi di transito degli elettroni nel fotomoltiplicatore. Tali differenze di
tempi di transito sono dovute principlamente alla geometria asimmetrica del
fototubo: elettroni emessi in punti diversi del fotocatodo giungono all’anodo
(moltiplicati in numero) in tempi diversi. In media il tempo di transito degli
elettroni nel fotomoltiplicatore può essere valutato come
r
2me Ek
∆t =
e2 E 2
dove il termine Ek è la porzione di energia cinetica dovuta alla velocità ortogonale alla superficie del catodo dell’elettrone emesso.
Quando la finestra del fotomoltiplicatore viene chiusa, al catodo si può rilevare una corrente di fondo residua. Questo dark-noise o dark-current può essere
attribuito a diversi fattori:
• emissione termoionica da parte del catodo o dei dinodi (fattore principale);
• perdite di corrente;
• contaminazioni radioattive;
• fenomeni di ionizzazione e conseguente creazione di portatori di carica
accelerati dal campo E;
• perdita di isolamento dalla radiazione elettromagnetica dell’involucro del
fototubo.
Essendo il fattore termoionico predominante rispetto alle altre fonti di rumore, si può ridurre la temperatura di funzionamento del fototubo per ridurre
in modo consistente il rumore di fondo.
I fotomoltiplicatori sono dispositivi sensibili alla luce: è quindi importante
assicurarsi che non ricevano una illuminazione diretta. Quando sono scollegati
la luce incidente nel fototubo (se non è di minima intensità come quella proveniente dagli scintillatori) potrebbe portare ad un aumento della corrente di buio,
fenomeno destinato ad annullarsi in un tempo dipendente dall’energia cui è stato sottoposto il trasduttore. Se invece un fotomoltiplicatore alimentato viene
esposto alla luce dell’ambiente si genera una extracorrente e un conseguente
stress del componente che potrebbe anche danneggiarsi irrimediabilmente.
L’efficienza del fototubo può essere ridotta a causa della presenza di campi
magnetici esterni che deviano il normale flusso degli elettroni accelerati. A tal
2.1 Introduzione e fisica dell’esperienza
69
fine spesso si ricopre il fototubo con uno strato metallico per schermare un eventuale campo magnetico esterno.
La stabilità del guadagno del fotomoltiplicatore può essere alterata da fenomeni di drift (di guadagno) o shift (nel tempo): entrambi alterano il guadagno
di circa 1%, quindi sono difficilmente rilevabili.
2.1.4
Logica NIM
I segnali elettrici possono essere classificati in segnali veloci e lenti. Mentre i
primi sono più adatti per operazioni di conteggio di eventi in tempi brevi i secondi sono meno affetti da disturbi e da rumore di fondo. In generale debbono
essere trattati con circuiti differenti, in quanto il tempo di tansito di un segnale
veloce all’interno di un circuito (quale ad esempio un amplificatore) deve essere
controllato ed inoltre i segnali veloci possono essere alterati dalla presenza di induttanze e condensatori all’interno della catena che causano correnti parassite,
fonti di errori sistematici nella misura.
In caso di segnali veloci come quelli provenienti da rivelatori di particelle
è importante la lunghezza dei collegamenti elettrici, che deve essere la minima
compatibile con la disposizione dell’apparato strumentale, e la loro impedenza.
Un altro fattore importante sono le riflessioni (fenomeni di eco) di segali all’interno dei collegamenti: tali riflessioni possono essere controllate terminando con
opportune impedenze i terminali liberi (non collegati ad altri devices).
Nella fisica dei rivelatori si utilizza lo standard NIM che prevede tutte le
possibili cause di rumore ed è studiato per il trasporto e l’analisi di segnali veloci o lenti. I moduli sono compatibili con entrambi i tipi di segnale, tuttavia
è necessario adattare le impedenze in modo opportuno qualora sia necessario
mescolare i due tipi di segnale elettrico nella stessa catena.
Tutto l’apparato in standard NIM deve avere tempi di risposta molto rapidi
e deve poter operare ad elevate frequenze per evitare la perdita o la sovrapposizione di eventi successivi.
Lo standard NIM accetta moduli di elaborazione del segnale analogico e
digitale o convertitori ADC-DAC. La logica NIM prevede uno standard positivo
per segnali lenti e negativo per segnali veloci. Per questi ultimi sono previsti
cavi coassiali con impedenza 50 Ω e tempi di salita dei circuiti non superiori a
1ns.
Discriminatori
Sono devices in logica NIM che trasformano un segnale analogico (quale quello
proveniente da un fotomoltiplicatore) in un segnale digitale (adatto al conteggio
di eventi). Ogni qual volta la tensione supera un certo valore di soglia (threshold) il discriminatore fornisce un segnale logico 1, mentre in caso opposto il
segnale logico è 0. Ottimizzando opportunamente il valore di threshold è pos-
70
Rivelazione di raggi cosmici
sibile selezionare alcuni eventi che forniscano un segnale analogico di una certa
entità.
Discriminatori differenziali
Operano come i discriminatori, ma forniscono un valore logico 1 solo se la tensione analogica è compresa all’interno di un determinato range. Solitamente
sono presenti più discriminatori differenziali in un unico modulo, in modo tale
da poter eseguire conteggi di eventi diversi discriminabili da diversi range di
tensione. Ad esempio è possibile (ammettendo di lavorare nella zona di linearità del rivelatore) contare il numero di particelle di data energia che impattano
lo scintillatore in un certo intervallo di tempo e misurare sperimentalmente una
curva di conteggi in funzione dell’energia.
Shaper
Questi devices accettano impulsi di diversa ampiezza e durata nel tempo e li
trasformano in segnali logici di ampiezza determinata e di predefinita durata di
tempo.
Delayer
Una volta che il segnale analogico è stato convertito con metodi diversi in un
segnale logico è possibile eseguire operazioni logiche di addizione o confronto di
più segnali. Ad esempio qualora si voglia verificare che un evento A sia avvenuto
in corrispondenza di un evento B occorre sommare logicamente i due segnali.
Tuttavia è possibile che i due segnali, provenienti da catene di elaborazione diverse (diversi sensori e diversi stadi di elaborazione del segnale), siano affetti da
ritardi non confrontabili. In questo caso il modulo NIM incaricato di verificare
la coincidenza potrebbe non eseguire in modo corretto l’operazione.
È quindi necessario procedere a inserire in una catena o in entrambe un ritardo opportuno. Questo ritardo viene inserito mediante delayer digitali.
Occorre ricordare che i moduli di delay inseriscono un offset temporale
standard, come indicato sul modulo stesso. Tale ritardo sistematico è dovuto
essenzialmente ai tempi di transito del segnale nel modulo.
Moduli di coincidenza e porte logiche
Vi sono spesso all’interno della catena NIM dei moduli che svolgono operazioni
logiche sui segnali. Generalmente si tratta di porte logiche che operano in standard di tempo di risposta e di logica NIM.
In particolare possiamo trovare porte AND e OR che accettano due dati in
ingresso e forniscono in uscita un valore logico secondo le seguenti tabelle di
verità:
2.1 Introduzione e fisica dell’esperienza
A B
0 0
0 1
1 0
1 1
AND
0
0
0
1
71
OR
0
1
1
1
Le porte OR possono essere assimilate al prodotto dei due ingressi, mentre
le porte AND alla somma degli ingressi (normalizzata all’unità).
Inoltre si possono avere porte NOT che accettano un unico valore in ingresso
e danno in uscita il valore negato:
A NOT
0
1
1
0
Applicare al segnale una porta NOT equivale a moltiplicarlo per -1.
I moduli di coincidenza comparano due o più segnali logici e verificano se essi
sono nello stesso istante nello stato 1. I segnali possono essere anche non perfettamente coincidenti, ovvero possono avere un breve ritardo tra loro, tuttavia
devono essere tali per cui la coincidenza è verificata per un tempo pari al tempo di risoluzione del modulo (nel caso della logica NIM tale tempo è di circa 3ns).
All’uscita delle porte logiche il segnale viene conformato in modo che abbia lunghezza e ampiezza standard per essere conteggiato mediante uno scaler.
Solitamente si trova su ciascun modulo una vite di regolazione della larghezza
del segnale.
25ns
0
1
Segnali non coincidenti
0
1
0
1
Segnali coincidenti
0
1
0
1
Segnali parzialmente coincidenti
0
1
3ns (max)
Figura 2.6: Schema delle coincidenze
72
2.2
Rivelazione di raggi cosmici
Osservazione del rumore di fondo
Somando gli effetti della corrente di buio dello scintillatore e del rumore di
fondo del fotomoltiplicatore è possibile rilevare in uscita picchi di segnale non
associabili ad alcun evento fisico. L’entità di questa componente del segnale è
un parametro da stimare in modo accurato, in quanto permette di stabilire le
soglie di misura. Ovviamente occorre procedere ad una misura per ciascun elemento rivelatore, in quanto in generale ci si può attendere rumori di fondo non
confrontabili su catene di misura diverse, sebbene composte da elementi dello
stesso tipo (ad esempio due scintillatori organici plastici possono comportarsi
in maniera differente).
Rivelatore organico plastico
Fotomoltiplicatore
-2200V
out
-2000V
out
Fotomoltiplicatore
Rivelatore organico liquido
Figura 2.7: Rivelatori di particelle: scintillatori e fotomoltiplicatori
Si hanno a disposizione tre rivelatori organici: due di tipo plastico e uno
di tipo liquido. Il setup sperimentale consta nella disposizione dei rivelatori
con i fotomoltiplicatori annessi e dell’esecuzione dei collegamenti. Per ciascun
fototubo è disponibile nel cradle apposito un alimentatore in grado di fornire
tensioni accoppiate negative di intensità variabile. Occorre collegare le uscite
di tali dispositivi ai fotomoltiplicatori corrispondenti. Prima di accendere gli
alimentatori occorre accertarsi che la tensione in uscita sia piccola. Dopo l’accensione è possibile aumentare la tensione a piccoli passi, sino al raggiungimento
della tensione di lavoro standard (-2200 V per i fototubi accoppiati a scintillatori
plastici e -2000 V per il fotomoltiplicatore dello scintillatore a liquido). In modo
analogo prima di spegnere l’alimentazione è consigliato ridurre a valori prossimi allo zero la tensione di alimentazione dei fototubi al fine di evitare possibili
sbalzi.
Una volta raggiunte le tensioni opportune si procede alla misura della tensione di rumore collegando di volta in volta l’uscita di un fototubo ad un oscilloscopio molto rapido (100 MHz di fondoscala sull’asse dei tempi). Si imposta un
valore di persistenza dell’immagine di qualche secondo e si verifica che l’uscita
dei picchi più alti sia dell’ordine dei 100 mV. Si nota che in questa configurazione tutti i segnali sono negativi, quindi il trigger dovrà essere impostato
2.2 Osservazione del rumore di fondo
73
per agire su rampe con derivata negativa (discese). Se si imposta un livello di
trigger più basso emerge una componente del segnale costante nel tempo che
si infittisce agendo opportunamente anche sulla persistenza dell’immagine. Il
trigger correttamente impostato si è rivelato un buon metodo per selezionare il
rumore di fondo dell’apparato.
È da ricordarsi che i cavi da utilizzare sono di tipo NIM, quindi è consigliato scegliere cavi con tempi di percorrenza simili su tutti i rivelatori, al fine di
evitare delay troppo elevati, non controllabili nelle fasi successive. Inoltre tutti
i terminali liberi, compresi quelli presenti sui moduli, devono essere terminati
con un’impedenza da 50 Ω.
Una volta raggiunta una regolazione opportuna si può bloccare l’acquisizione
dello strumento e salvare i dati grafici oltre che misurare l’altezza del picco mediante cursori orizzontali.
Analizzando la forma della risposta di ciascuno scintillatore si nota che lo
scintillatore liquido ha un tempo di salita maggiore rispetto agli scintillatori
plastici che presentano riposte simili.
Figura 2.8: Risposta del rivelatore A per un cosmico incidente
Abbiamo alimentato i fotomoltiplicatori con le seguenti tensioni:
VhA = −2200[V ] scintillatore plastico - A
VhB = −2200[V ] scintillatore plastico - B
VhC = −2000[V ] scintillatore liquido - C
I valori di soglia sono stati selezionati dal segnale tenendo conto di due fattori: il valore di soglia è un valore pressochè costante nel tempo e attorno a
questo valore si addensa un gran numero di valori; inoltre abbiamo considerato che i raggi cosmici hanno una coda molto allargata e di forma costante. Il
rumore di fondo ha forme diverse e in particolare si possono osservare curve anche distanti dal picco centrale di ampezza confrontabile con il picco di rumore.
74
Rivelazione di raggi cosmici
Figura 2.9: Risposta del rivelatore B per un cosmico incidente
Figura 2.10: Risposta del rivelatore C per un cosmico incidente
Questi sono i risultati delle misure eseguite.
VnoiseA = −37.1[mV ] scintillatore plastico - A
VnoiseB = −41.2[mV ] scintillatore plastico - B
VnoiseC = −55.2[mV ] scintillatore liquido - C
La determinazione del rumore di fondo con queste modalità fornisce un
parametro non molto oggettivo, infatti abbiamo verificato che le curve sono
sovrapposte e il picco centrale del rumore, rappresentato da una traccia più
intensa e quindi indice della sovrapposizione di più segnali simili registrati in
tempi successivi, presenta una coda abbastanza importante che sfuma verso il
basso. Per scegliere un valore coerente in tutte le misure abbiamo deciso di
tagliare la coda del picco. Nello scintillatore liquido è stato tuttavia più difficile
identificare la netta divisione tra il picco e la coda.
2.3 Determinazione della tensione di lavoro dei fototubi
75
La determinazione del rumore di fondo della catena di misura serve per
impostare il discriminatore in modo opportuno. In generale si sceglie un valore
di soglia superiore al valore di noise, in modo tale da selezionare gli eventi.
Abbiamo potuto verificare nel caso dello scintillatore liquido che, se il rumore
di fondo è dell’ordine di -40 mV, i raggi cosmici producono segnali dell’ordine
di circa -80 mV, quindi la soglia può essere impostata anche a valori superiori
(in modulo) rispetto al Vnoise . La scelta della soglia opportuna in relazione
con la tensione di lavoro dei fototubi deve essere verificata con altri metodi ed
eventualmente corretta in seguito.
2.3
Determinazione della tensione di lavoro dei
fototubi
Le tensioni di soglia si regolano mediante l’apposita vite posta sul fronte del
modulo; la tensione di soglia può essere letta mediante un voltmetro collegato
alla boccola di test (i valori letti in mV devono essere poi divisi per 10). È
stato scelto di impostare una soglia pari a 1.2 volte l’ampiezza del rumore, per
eliminare la tensione di buio e contemporanamente non tagliare troppo le informazioni relative ai cosmici meno energetici. Sono state selezionate le seguenti
tensioni di soglia per ciascun canale del discriminatore.
HighVoltage
A
Discriminatore
Scaler
A
HighVoltage
B
Discriminatore
Scaler
C
HighVoltage
C
Scaler
B
Discriminatore
Figura 2.11: Setup sperimentale: misura della HV
VnoiseA = −44.5[mV ] scintillatore plastico - A
VnoiseB = −49.5[mV ] scintillatore plastico - B
VnoiseC = −62.2[mV ] scintillatore liquido - C
Gli ingressi del discriminatore devono essere collegati ai tre fotomoltiplicatori e terminare con resistenze da 50 Ω; le uscite dello stesso vanno inviate agli
ingressi dello scaler (dopo il discriminatore i segnali sono NIM digitali).
76
Rivelazione di raggi cosmici
Al fine di poter confrontare i valori di scintillatori di dimensioni diverse
occorre misurare la superficie sensibile di ciascuno di essi e calcore il rate (il
numero di eventi contati dallo scaler ingloba la dipendenza dalla superficie del
sensore).
A → (73.0x16.0 ± 0.1)[cm]
B → (73.0x16.0 ± 0.1)[cm]
C → (80.0x80.0 ± 0.1)[cm]
Le misure geometriche dei rivelatori sono state eseguite con un metro, considerando solo la parte sensibile di ciascuno scintillatore. Tuttavia sono state
considerate le misure esterne del rivelatore, trascurandone lo spessore delle
pareti. A causa di questo fatto, tali misure possono essere affette da errori
sistematici.
Aumentando la tensione di alimentazione dei fotomoltiplicatori si può massimizzare l’efficienza del rivelatore, tuttavia oltre un certo limite di tensione
l’efficienza non migliora, mentre il rumore di fondo aumenta in modo sensibile.
La situazione ideale è porsi nelle condizioni in cui l’efficienza è massima, pur non
superando di molto il valore di saturazione del device al fine di mantenere un
rapporto segnale/rumore favorevole. Al fine di determinare sperimentalmente
la tensione di lavoro ottimale è possibile eseguire più misure di rate a tensioni
diverse per ciacun device. Si osserva una crescita dei conteggi proporzionale
all’aumento della tensione sino ad un valore limite, oltre il quale il numero di
conteggi rimane costante. La tensione di lavoro non deve superare la tensione
massima di alimentazione dichiarata dal costruttore del device e non deve essere inferiore al minimo di lavoro, altrimenti il rivelatore non funziona in modo
corretto.
Al fine di misurare l’errore sulla determinazione del numero√
di eventi occorre
ricordare che una misura di eventi x è affetta da un errore δx = x. Per ottenere
un errore inferiore al 3% della misura occorre considerare tempi di acquisizione
che permettano conteggi superiori a 1000 eventi.
Selezionando la tensione di lavoro al limite inferiore del plateau si nota un
incremento sensibile dei conteggi di alcuni ordini di grandezza superiori al valore
atteso. Questo fatto può essere spiegato analizzando il segnale mediante l’oscilloscopio: si nota che il rumore è aumentato in modo sensibile. Si è quindi scelto
di abbassare le tensioni di alimentazione dei fotomoltiplicatori (diminuendone
quindi il guadagno) rispetto al valore di limite del plateau al fine di ottenere
conteggi confrontabili con il valore atteso o leggermente superiori.
VhA = −2220[V ] scintillatore plastico - A
VhB = −2220[V ] scintillatore plastico - B
VhC = −2050[V ] scintillatore liquido - C
Si può quindi impostare un tempo di acquisizione dell’ordine di 100s e
provare il rate di ciascuna catena, ripetendo le misure alcune volte. Lo scopo è
di determinare se i cosmici rivelati da A e B, scintillatori plastici con la stessa
superficie sensibile, appartengano alla stessa popolazione.
2.3 Determinazione della tensione di lavoro dei fototubi
HV
-1700[V]
-1750
-1800
-1850
-1900
-1950
-2000
-2050
-2100
-2150
-2200
-2250
-2275
-2300
-2325
-2350
-2400
-2450
-2500
-2550
-2600
δHV
1[V]
A
δA
B
δB
9
39
110
269
574
943
1896
8526
13553
17620
22085
25190
32763
41643
54089
71060
99048
3
6
10
16
24
31
44
92
116
133
149
159
181
204
233
267
315
18
35
115
347
679
1183
2175
10426
16144
21744
31913
35517
46438
55667
64505
82662
101575
4
6
11
19
26
34
47
102
127
147
179
188
215
236
254
287
319
C
2616
3355
4118
5004
5776
6784
8368
10989
11182
19367
77
δC
51
58
64
71
76
82
91
105
106
139
Tabella 2.1: Misura di eventi al variare di HV - ∆T = 100.000s
A
2275
2234
2091
2468
2383
2229
2011
2392
2141
2077
2270
2163
2257
2462
2186
B
2320
2299
2013
2114
2092
2402
2271
2038
2495
2175
2085
2302
2135
2270
2028
C
12027
12200
12462
12402
12020
12344
11812
12148
12197
12108
11917
12353
11968
12317
11786
Tabella 2.2: Misura di eventi sui singoli rivelatori - ∆T = 100.000s
Il rumore di fondo può essere eliminato osservando le coincidenze tra i diversi
segnali. Il rumore di fondo di ciascun fotomoltiplicatore è infatti scorrelato da
quello generato dagli altri due, non essendo generato dal passaggio di raggi
cosmici. Eseguendo le misure in coincidenza il rumore di fondo viene eliminato
dal conteggio, sebbene alcuni errori statistici possono essere dovuti a coincidenze
casuali. Se al contrario la soglia è troppo bassa (in modulo e ad una fissata
tensione di alimentazione del fototubo) alcuni eventi non vengono conteggiati e
vengono persi anche nelle coincidenze.
78
Rivelazione di raggi cosmici
2.3.1
Elaborazione dati
Sono stati calcolati i rates per ciascuna misura di eventi sui singoli scintillatori
al variare della tensione di alimentazione dei fotomoltiplicatori, tenendo conto
di un tempo di acquisizione di 100000 ± 1[ns]. L’informazione molto precisa sul
tempo di acquisizione permette di valutare come poco apprezzabile la prozione
di incertezza addotta da questa grnadezza nel calcolo dell’incertezza dei rates.
HV [V]
-1700±1
-1750
-1800
-1850
-1900
-1950
-2000
-2500
-2100
-2150
-2200
-2250
-2275
-2300
-2325
-2350
-2400
-2450
-2500
-2550
-2600
(A + B) ∗ C [Hz]
δ(A+B)∗C [Hz]
0.09
0.39
1.1
2.7
5.7
9.4
19.0
85.3
136
176
221
252
328
416
541
711
990
0.03
0.06
0.1
0.2
0.2
0.3
0.4
0.9
1
1
1
2
2
2
2
3
3
A + B [Hz]
0.18
0.35
1.2
3.5
6.8
11.8
21.8
104
161
217
319
355
464
557
645
827
1016
δA+B [Hz]
0.04
0.06
0.1
0.2
0.3
0.3
0.5
1
1
1
2
2
2
2
3
3
3
C [Hz]
δC [Hz]
26.2
33.6
41.2
50.0
57.8
67.8
83.7
110
112
194
0.5
0.6
0.6
0.7
0.8
0.8
0.9
1
1
1
Tabella 2.3: Misura della curva di coincidenza sperimentale - rates
I rates sono quindi stati plottati in scala logaritmica per verificarne l’andamento. Le discontinuità presenti in maniera più o meno accentuata su tutte e
tre le curve evidenziano che in questi punti il rumore dei fotomoltplicatori aumenta in modo sensibile e in particolare supera la soglia impostata sui rispettivi
discriminatori.
I dati ottenuti dalla√misura di popolazioni sono stati elaborati calcolandone
l’errore, stimato come n, essendo i dati distribuiti secondo una distribuzione
poissoniana con probabilità pari a 12 . I rate è stato calcolato dividendo il numero
di conteggi per il tempo di acquisizione, fissato a 100.000 ± 0.001[s].
A
2275
2234
2091
2468
2383
2229
2011
2392
2141
2077
2270
2163
2257
2462
2186
σA
48
47
46
50
49
47
45
49
46
46
48
47
48
50
47
RA [Hz]
22.75
22.34
20.91
24.68
23.83
22.29
20.11
23.92
21.41
20.77
22.70
21.63
22.57
24.62
21.86
σRA [Hz]
0.48
0.47
0.46
0.50
0.49
0.47
0.45
0.49
0.46
0.46
0.48
0.47
0.48
0.50
0.47
B
2320
2299
2013
2114
2092
2402
2271
2038
2495
2175
2085
2302
2135
2270
2028
σB
48
48
45
46
46
49
48
45
50
47
46
48
46
48
45
RB [Hz]
23.2
22.99
20.13
21.14
20.92
24.02
22.71
20.38
24.95
21.75
20.85
23.02
21.35
22.70
20.28
σRB [Hz]
0.48
0.48
0.45
0.46
0.46
0.49
0.48
0.45
0.50
0.47
0.46
0.48
0.46
0.48
0.45
C
12027
12200
12462
12402
12020
12344
11812
12148
12197
12108
11917
12353
11968
12317
11786
σC
110
110
112
111
110
111
109
110
110
110
109
111
109
111
109
Tabella 2.4: Rate di eventi singoli - ∆T = 100.000s
RC [Hz]
120.27
122.00
124.62
124.02
120.20
123.44
118.12
121.48
121.97
121.08
119.17
123.53
119.68
123.17
117.86
σRC [Hz]
0.48
0.47
0.46
0.50
0.49
0.47
0.45
0.49
0.46
0.46
0.48
0.47
0.48
0.50
0.47
2.3 Determinazione della tensione di lavoro dei fototubi
79
Log@rateD
6
4
2
0
-2
2000
2100
2200
2300
2400
2500
2600
-HV @VD
Figura 2.12: Rates misurati da A in funzione di HV
Log@rateD
6
4
2
0
2000
2100
2200
2300
2400
2500
2600
-HV @VD
Figura 2.13: Rates misurati da B in funzione di HV
Per ogni set di dati provenienti da ciascuno scintillatore sono stati calcolati
il valor medio e la deviazione standard del valor medio
A = 2243[Hz]
σA = 36[Hz]
σA = 1.6%
B = 2203[Hz]
σB = 38[Hz]
σB = 1.7%
80
Rivelazione di raggi cosmici
Log@rateD
6
5.5
5
4.5
4
3.5
1800
1900
2000
2100
-HV @VD
Figura 2.14: Rates misurati da C in funzione di HV
C = 12137[Hz]
σC = 55[Hz]
σC = 0.5%
Mediante un test di Student è stata verificata con un margine di errore del 5%
l’appartenenza alla stessa popolazione dei raggi cosmici incidenti sui rivelatori
A e B (aventi la stessa superficie sensibile):
t= q
|xA − xB |
2
2
(N −1)σXA
+(N −1)σXA
2N −2
= 1.088 < tc = 1.7
Il risultato positivo del test permette di asserire con un margine di errore del
5% che i raggi cosmici incidenti sulle due superfici sensibili di A e B appartengono alla stessa popolazione come intuitivamente è prevedibile.
Proseguendo nell’analisi sono stati calcolati i valori dei rates normalizzati
per unità di superficie sensibile.
RA = 192.0 ± 3.3[Hzm−2]
RB = 188.6 ± 3.5[Hzm−2]
RC = 189.6 ± 0.9[Hzm−2]
Si può notare che la determinazione del tempo di acquisizione è molto precisa e l’incertezza associata a questa grandezza influisce nella propagazione degli
errori per qualche decimo di parte su mille. Si può quindi considerare il tempo
di acquisizione come una costante esatta, trascurandone l’incertezza.
Si può notare che i rates medi sono confronatbili tra loro, tuttavia approssimano per ecesso il rate atteso R = 180[s−1 m−2 ]. Questo è dovuto al fatto che
2.4 Misura della curva di coincidenza
81
sono state impostate tensioni di soglia troppo basse (in modulo). Questa scelta
è stata fatta per avere una certa sicurezza di conteggiare tutti i cosmici, ma in
questo caso il rate evidenzia che vengono conteggiati come cosmici anche alcuni
segnali di rumore. Questo errore sistematico verrà corretto mediante il conteggio dei cosmici in coincidenza di più rivelatori.
È possibile confrontare questi valori tra loro, mediante tests di Student, per
valutare se anche i cosmici che incidono il rivelatore C siano appartenenti alla
stessa popolazione di quelli rivelati dagli scintillatori A e B. I tests sono stati
eseguiti con le stesse modalità del test precedente.
tAB = 1.01
tAC = 0.97
tBC = 0.42
DF = 28 → tc = 1.7
Tutti i tests eseguiti hanno confermato, con una probabilità di errore del 5%,
che i cosmici incidenti sulle tre superfici appartengono alla stessa popolazione.
2.4
Misura della curva di coincidenza
Essendo i segnali inviati allo scaler di tipo logico è possibile eseguire operazioni
logiche su di essi quali AND e OR. In particolare si vuole determinare il numero
di coincidenze, ovvero il numero di eventi rivelati contemporaneamente dallo
scintillatore liquido e dai due scinitillatori plastici, considerati un unico rivelatore: occorre in altre parole misurare il numero di eventi di [(A or B) and C].
A tal fine occorre verificare che i segnali forniti in uscita dai discriminatori siano confrontabili in termini di larghezza. Si può visualizzare il segnale
prodotto dal device mediante un oscilloscopio. Il segnale è composto da una
serie di onde quadre di altezza -800mV in corrispondenza della rivelazione di
un probabile evento. La larghezza di ciascun segnale è regolata mediante un
potenziometro posto sul modulo discriminatore. È stata scelta una larghezza a
mezza altezza (FWHM) di ciascun segnale pari a 25ns.
I segnali logici sono quindi inviati ai moduli di addizione e coincidenza, secondo quanto riportato nel diagramma a blocchi. La larghezza del segnale dopo
il modulo di addizione deve essere impostata a 25ns, in modo analogo a quanto
già eseguito in precedenza.
Il valore scelto per la larghezza del segnale determina il tempo di risoluzione
dell’apparato. È quindi importante che sia un tempo piccolo; tuttavia si deve
tenere conto della capacità dello scaler di discriminare due eventi consecutivi,
quindi non può essere un tempo troppo breve. Inoltre una larghezza maggiore
rende il modulo di coincidenza meno sensibile a eventuali ritardi non sistematici
del segnale.
I moduli di delay inseriti nella catena servono a compensare eventuali differenze di tempo presenti. I ritardi, che sono pressoché costanti (e distribuiti
82
Rivelazione di raggi cosmici
A: scintillatore organico plastico
B: scintillatore organico plastico
C: scintillatore organico liquido
B
A
C
Figura 2.15: Disposizione dei rivelatori per la determinazione della curva di
coincidenza
in modo normale), possono essere causati da diversi tempi di salita dello scintillatore e del relativo fototubo, da cavi di lunghezza diversa (e quindi tempi di
transito del segnale diversi) o da tempi di risposta dei vari apparati non confrontabili tra loro.
Al fine di determinare il ritardo che permette di sincronizzare i segnali che
giungono al modulo di coincidenza occorre procedere ad un analisi sistematica:
si contano gli eventi [A or B], [C] e [(A or B) and C], con tempi di acquisizione
dell’ordine della decina di minuti impostando ad ogni misura tempi di ritardo
diversi a step fissi, sia su un canale che sull’altro. Graficando la curva di coincidenza in funzione del ritardo si prevede di ottenere un grafico simmetrico
attorino al valore ottimale di ritardo.
Le misure sono state eseguite su tempi di 600 s. Il ritardo è stato impostato
a step di 4ns. Si considerano positivi i ritardi impostati sulla catena dei conteggi dei rivelatori plastici. Le misure sono state eseguite impostando diversi
ritardi, al fine di determinare la risoluzione temporale dell’apparato di misura
e il ritardo ottimale da impostare al fine di verificare le corrette coincidenze.
Tale tempo di ritardo può essere previsto teoricamente, seppur con una certa
imprecisione, considerando le lunghezze dei cavi inseriti in ciascun canale e i
tempi di percorrenza del segnale in ciascun modulo che costituisce la catena
NIM; tuttavia una determinazione sperimentale è necessaria per ridurre possibili cause di errori sistematici.
Il setup sperimentale, come rappresentato in figura 2.16, consiste nella costruzione di due catene di segnali logici che dovrebbero conteggiare gli stessi
eventi. Gli scintillatori plastici (A e B), posti al di sopra dello scintillatore a
liquido (C), sono adiacenti, in modo tale da costituire una superficie sensibile
di dimensioni prossime a quella del rivelatore a liquido. Si vuole determinare
la coincidenza della rivelazione di un raggio cosmico da parte di uno dei due
scintillatori plastici e dello scintillatore liquido.
I tre scintillatori sono alimentati con le tensioni ricavate nella precedente
2.4 Misura della curva di coincidenza
83
HighVoltage
A
Discriminatore
OR
HighVoltage
B
A+B
Discriminatore
Scaler
A+B
ch1 ch2
Discriminatore
AND
(A+B)*C
Scaler
C
Scaler
(A+B)*C
HighVoltage
C
Delay
C
Delay
Figura 2.16: Setup sperimentale: misura della curva di coincidenza
parte dell’esperienza e sono collegati ai tre discriminatori (le tensioni di soglia
sono rimaste invariate rispetto al setup precedente). I segnali logici provenienti
dai due scintillatori sono addizionati mediante un modulo OR. I segnali nei due
circuiti transitano in due delayer, quindi vengono analizzati mediante un modulo di coincidenza logica. Allo scaler sono inviati i segnali provenienti dal modulo
di coincidenza, dal modulo OR e dal discriminatore collegato al rivelatore C,
su canali separati. È possibile inserire un oscilloscopio (dotato di impedenza
corretta) nella catena logica dei segnali, in modo da verificare nel corso della
misura le impostazioni e le variazioni del segnale in base alle scelte fatte.
2.4.1
Acquisizione dati
È stato scelto un tempo di acquisizione di 600.000 s per ciascuna misura.
La larghezza dei segnali logici è stata impostata per un tempo di 25 ns su
entrambe le linee ed è stato verificato questo valore collegando l’oscilloscopio
digitale all’uscita di ciascun rivelatore (è stata considerata la larghezza a mezza
altezza del segnale) e a valle dei moduli logici.
La misura è iniziata impostando ritardi sulla linea dei rivelatori plastici
(ritardi positivi), quindi sono state azzerate le impostazioni e si sono inseriti
ritardi sulla linea dello scintillatore liquido. Inizialmente è stato scelto uno step
di ritardo di 4ns, poi, dopo aver messo in grafico i dati ottenuti, sono state prese
delle misure aggiuntive in alcuni punti intermedi.
2.4.2
Risultati
Dai dati acquisiti sono stati calcolati i rates di cosmici, considerando tempi di
acquisizione pari 600.000 ± 0.001[s].
84
Rivelazione di raggi cosmici
DeltaT [ns]
-48±1
-44
-40
-38
-36
-34
-32
-30
-28
-24
-20
-16
-12
-8
-4
0
4
8
10
12
14
16
20
24
28
32
(A + B) ∗ C
13
68
292
496
763
1136
1421
1576
1663
1697
1652
1680
1707
1626
1637
1655
1737
1573
1321
1133
822
486
297
136
95
66
δ(A+B)∗C
A+B
δA+B
C
δC
4
8
17
22
28
34
38
40
41
41
41
41
41
40
40
41
42
40
36
34
29
22
17
12
10
8
26156
26024
26066
26322
25486
25820
25858
26119
26438
26320
26093
26264
26372
25942
25875
25151
25553
25860
26472
25615
26462
25339
25675
26067
26081
26019
162
161
161
162
160
161
161
162
162
162
162
162
162
161
161
159
160
161
163
160
163
159
160
161
161
161
78306
77959
78192
76734
77417
77544
77569
77879
77769
78141
77969
77847
77815
76983
77457
74919
74955
74805
77455
74715
77739
75002
74605
74635
74900
74779
280
279
280
277
278
278
279
279
279
280
279
279
279
277
278
274
274
274
278
273
279
274
273
273
274
273
Tabella 2.5: Misura della curva di coincidenza sperimentale
DeltaT [ns]
-48±1
-44
-40
-38
-36
-34
-32
-30
-28
-24
-20
-16
-12
-8
-4
0
4
8
10
12
14
16
20
24
28
32
(A + B) ∗ C
0.022
0.113
0.49
0.83
1.27
1.89
2.37
2.63
2.77
2.83
2.75
2.80
2.85
2.71
2.73
2.76
2.89
2.62
2.20
1.89
1.37
0.81
0.49
0.23
0.16
0.110
δ(A+B)∗C
A+B
δA+B
C
δC
0.006
0.014
0.03
0.04
0.05
0.06
0.06
0.07
0.07
0.07
0.07
0.07
0.07
0.07
0.07
0.07
0.07
0.07
0.06
0.06
0.05
0.04
0.03
0.02
0.02
0.014
43.6
43.4
43.4
43.9
42.5
43.0
43.1
43.5
44.1
43.9
43.5
43.8
43.9
43.2
43.1
41.9
42.6
43.1
44.1
42.7
44.1
42.2
42.8
43.4
43.5
43.4
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
0.3
130.5
129.9
130.3
127.9
129.0
129.2
129.3
129.8
129.6
130.2
129.9
129.7
129.7
128.3
129.1
124.9
124.9
124.7
129.1
124.5
129.6
125.0
124.3
124.4
124.8
124.6
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
Tabella 2.6: Misura della curva di coincidenza sperimentale - rates
I rates della coincidenza sono stati rappresentati in un grafico, in funzione del
ritardo impostato. Il grafico ha un andamento simmetrico rispetto ad un valore
di tensione intorno a -10 [ns] (ritardo positivo impostato sui segnali provenienti
dal rivelatore C).
2.4 Misura della curva di coincidenza
85
rate @HzD
3
2.5
2
1.5
1
0.5
-40
-20
20
ritardo @nsD
Figura 2.17: Coincidenze in funzione del ritardo
I dati vengono interpolati mediante una serie di tre fit lineari, uno per il tratto a derivata positiva, uno per il tratto a derivata negativa e uno sulla regione di
plateau costante. Sono stati eliminati dai fit i punti iniziali e finali, costituenti
le code esterne del grafico. La bontà dei tre fit è stata valutata con tests del χ 2
(abbiamo ottenuto fit corretti con una probabilità massima di errore del 1%)
(y=a+bx).
Tratto a derivata positiva
ρ = 0.994
a = 9.5 ± 0.2[Hz]
b = 0.225 ± 0.005[Hz ns−1 ]
χ2 = 3.29
DF = 4 → χ2critico = 3.32
Plateau
ρ = 0.11
a = 2.79 ± 0.03[Hz]
b = 0.000 ± 0.002[Hz ns−1 ]
χ2 = 1.6
DF = 7 → χ2critico = 2.6
Tratto a derivata negativa
ρ = −0.994
a = 4.5 ± 0.1[Hz]
b = −0.223 ± 0.008[Hz ns−1 ]
χ2 = 2.96
DF = 3 → χ2critico = 3.78
Per il tratto costante si confronta il coefficiente angolare della retta con il
valore atteso (0) attraverso test normale:
86
Rivelazione di raggi cosmici
rate @HzD
3
2
1
-40
-20
20
ritardo @nsD
-1
Figura 2.18: Coincidenze in funzione del ritardo - rette
z=
0.0006
= 0.37 < zc = 1.96
0.0016
Per ottenere la FWHM, rappresentante il tempo di risoluzione dell’apparato,
occorre intersecare le tre rette e valutare l’altezza del punto medio del plateau.
Considerandone la metà si costruisce una retta orizzontale e si verficano le intersezioni di quest’ultima con i tratti di salita e discesa. La distanza tra questi
due punti è la larghezza a metà altezza della curva, con la relativa incertezza
(ottenuta mediante propagazione).
F W HM = 49.5 ± 1.4[ns]
2.5
2.5.1
Misura di eventi accidentali
Setup sperimentale
Il setup sperimentale è analogo a quello realizzato nella parte precedente dell’esperienza, salvo che si imposta su un canale il ritardo massimo (nel corso
dell’esperineza è stato scelto un ritardo di 63 ns).
2.5.2
Acquisizione dati
La quantificazione di eventi accidentali (o meglio la determinazione del loro
rate) costituisce un valido modo per eliminare parte degli errori statistici cui
sono affette le misure di eventi. I rivelatori forniscono un segnale in uscita che
è composto da una parte di segnale realmente prodotto dall’impatto di raggi
cosmici sulla superficie sensibile del fototubo e da una parte di rumore a basso
2.5 Misura di eventi accidentali
87
voltaggio non imputabile all’azione di cosmici. Parte di questo rumore viene
eliminato impostando correttamente le soglie di lavoro dei discriminatori, tuttavia è possibile che una porzione dei conteggi misurati sia causata da rumore
avente componenti a tensione superiore alla soglia. In generale operando in
coincidenza con più rivelatori gli effetti del rumore di fondo si possono ulteriormente ridurre: il rumore di fondo produce infatti tensioni variabili nel tempo,
tuttavia non essendo legato ad alcun agente esterno al fotomoltiplicatore, i falsi
conteggi di un rivelatore difficilmente avvengono in coincidenza con quelli di un
altro, quindi questa informazione viene persa.
Non è tuttavia da escludere che una parte del rumore di fondo venga causata
da eventi accidentali che giungono al rivelatore in coincidenza.
Al fine di quantificare statisticamente il rate di accidentali occorre impostare
il delay in zone dove la curva di coincidenza è pressoché nulla, quindi procedere
a lunghe acquisizioni misurando tutti i rates (di entrambi i circuiti e della coincidenza), come nella parte precedente dell’esperienza (il setup è il medesimo). Gli
eventi accidentali sono pochi, se confrontati con gli eventi realmente provocati
da raggi cosmici, quindi per avere dati significativi l’acquisizione deve durare
parecchie ore.
Il rate di accidentali può essere stimato teoricamente analizzando i dati delle
due misure sui singoli ingressi del modulo di coincidenza: in tal caso il rate può
essere espresso come
Racc =
#accidentali
= RC RA+B τ
∆T
dove ∆T è il tempo di acquisizione, Rx è il rate della variabile x e τ è il tempo
di risoluzione dell’apparato, precedentemente determinato.
Nel calcolo del rate di questi eventi non occorre tener conto delle superfici
dei sensori, in quanto il rumore di fondo è prodotto non da un evento manifestatosi sulla superficie degli scintillatori, ma bensı̀ da fluttuazioni statistiche
della tensione di buio. Al limite si potrebbe pensare di valutare gli eventi accidentali sostituendo idealmente i rivelatori con generatori di funzioni random sia
in ampiezza che in frequenza.
Prima di iniziare con l’acquisizione è stato visualizzato sull’oscillosopio l’effettivo ritardo tra i due segnali all’ingresso del modulo di coincidenza. Il ritardo
previsto era di 63 ns, tuttavia si è osservato un ritardo superiore, dovuto a diversi offsets dei due segnali, dovuti principalmente a lunghezze di cavi diverse,
tempi di risposta dei rivelatori diversi e tempi di transito non uguali nei diversi
moduli (è stato utilizzato un unico delayer nel circuito di C e due moduli in serie nell’altro circuito, già affetto da un offset derivante dal modulo di addizione
logica).
2.5.3
Risultati
Al fine di ottenere dati confrontabili tra loro, è stata eliminata la dipendenza
dal tempo, calcolando i rates in ogni set di dati. Gli errori su ciascuna misura di
88
Rivelazione di raggi cosmici
(A + B) ∗ C
Tacq [s]
72210.990±0.009
68374.890±0.008
158374.880±0.017
387
364
879
δ(A+B)∗C
A+B
δA+B
C
δC
20
20
30
3055150
2964900
8842250
1748
1722
2974
9273436
6993787
20608339
3045
26645
4540
Tabella 2.7: Misura di eventi accidentali
Figura 2.19: Visualizzazione del delay massimo
eventi sono stati determinati mendiante la radice quadrata del numero di eventi
stesso, in quanto si suppongono appartenenti ad una distribuzione Poissoniana.
(A + B) ∗ C [Hz]
0.0054
0.0053
0.0056
δ(A+B)∗C [Hz]
A + B [Hz]
δA+B [Hz]
C
δC [Hz]
0.0003
0.0003
0.0002
42.31
43.36
55.83
0.02
0.02
0.02
128.42
102.29
130.12
0.04
0.04
0.03
Tabella 2.8: Rates di eventi accidentali
È possibile determinare il valore medio dei tre rates e stimarne l’errore
eseguendo medie pesate sulle incertezze:
R(A+B)C = 0.0054 ± 0.0001[Hz]
RA+B = 46.42 ± 0.01[Hz]
RC = 119.64 ± 0.02[Hz]
Il rate di accidentali può essere previsto in modo teorico osservando la
sovrapposizione massima dei segnali, ovvero
Racc = RA+B RC τ = R(A+B)C
2.6 Misura dell’efficienza di un rivelatore
89
Dove τ rappresenta il tempo di risoluzione dell’apparato strumentale stimato
come τ = 49.5 ± 1.4[ns].
Provando a calcolare questa grandezza in modo teorico si ottiene un risultato circa 20 volte inferiore a quello misurato sperimentalmente. Questo può
essere legato al fatto che la differenza tra il tempo di risoluzione e la separazione dei segnali impostata è insufficiente a prevenire che i segnali jitterando
si sovrappongano e vengano quindi conteggiati dallo scaler. I conteggi eseguiti
dall’apparato strumentale degli accidentali comprendono oltre agli accidentali
anche rumore in fase dati dai tre rivelatori.
Racc = 0.275 ± 0.008[mHz]
Il ritardo di tempo impostato risulta essere insufficiente per ottenere una
misura attendibile del numero di coincidenze accidentali: la misura ottenuta
sperimentalmente risulta infatti essere
Racc = 5.4 ± 0.1[mHz]
2.6
Misura dell’efficienza di un rivelatore
L’efficienza di un rivelatore è un parametro molto importante. Nelle misure di
fisica delle alte energie gli scintillatori sono spesso utilizzate come trigger per
misure successive: al fine di evitare perdite di dati su eventi spesso rari occorre
che l’efficienza di questi device sia molto prossima al 100%. Si raggiungono
efficienze del 99% per scintillatori nuovi e perfettamente accoppiati a fotomoltiplicatori correttamente tarati (HV e Vtr opportunamente settati).
A: scintillatore organico plastico
B: scintillatore organico plastico
C: scintillatore organico liquido
A
B
C
Figura 2.20: Disposizione dei rivelatori per la misura di efficienza
Al fine di determinare l’efficienza occorre sovrapporre più rivelatori verticalmente. I rivelatori divrebbero avere la stessa superficie sensibile, tuttavia nel
nostro caso il rivelatore a liquido C, avente una superficie maggiore, è posto
come ultimo rivelatore (il rivelatore in test di efficienza è il B), quindi questo
fatto non influisce sulla misura finale.
90
Rivelazione di raggi cosmici
Un raggio cosmico che attraversa i rivelatori B e C, per considerazioni geometriche deve necessariamente attravarsare anche il rivelatore A. Tuttavia è
possibile che il rivelatore B non riveli questo evento a causa di perdite dovute
all’efficienza del device.
Per quantificare l’efficienza si confrontano i rates di raggi cosmici giunti e
rivelati in coincidenza sui tre scintillatori e dei cosmici rivelati unicamente da
B e C. L’efficienza in questo caso può essere calcolata come
η=
# eventi A*B*C
# eventi B*C
Affinché un evento appaia in coincidenza su B e C esso dovrà accadere nella
regione sensibile di B e quindi la parte di C colpita dal raggio è unicamente
quella sottostante il rivelatore B (la superficie di A e B è la medesima).
L’efficienza viene misurata in funzione della tensione HV applicata all fotomoltiplicatore in esame. Tale parametro determina infatti il guadagno del
fotomoltiplicatore e quindi la capacità di risolvere raggi cosmici poco energetici.
2.6.1
Setup sperimentale
HighVoltage
A
Discriminatore
HighVoltage
B
Discriminatore
HighVoltage
C
Discriminatore
Delay
AND
A*B*C
AND
A*C
Scaler
A*B*C
Scaler
A*C
Figura 2.21: Setup sperimentale: misura di efficienza
L’apparato sperimentale deve essere configurato in modo tale che i due rivelatori plastici siano posti uno sopra l’altro e si debbono utilizzare due moduli di
coincidenza per conteggiare A*B*C e B*C. Il ritardo indicato nella figura relativa al setup sperimentale è puramente indicativo: nella pratica occorre inserire
i ritardi in modo opportuno affinché i segnali, osservati tramite un oscilloscopio,
giungano al modulo di coincidenza in contemporanea.
2.6 Misura dell’efficienza di un rivelatore
91
Le misure vengono eseguite impostando i valori di threshold come nell’esperienza precedente e lasciando invariate le tensioni di alimentazione dei fotomoltiplicatori. Per quanto riguarda il rivelatore in esame (A), si inizia con una
tensione di alimentazione al minimo di lavoro (-1900 [V]), quindi si procede aumentandola a step fissi, sino alla tensione massima applicabile al device. Per
ogni valore di tensione si eseguono misure con tempi di acquisizione di 10 minuti circa, al fine di aver sufficienti conteggi e quindi un errore percentuale non
troppo elevato. Si verifica tuttavia che a bassa tensione il numero di conteggi è
notevolmente inferiore, quindi l’errore relativo aumenta.
2.6.2
Acquisizione dati
La tensione minima scelta è stata di -1900 [V], i tempi di acquisizione per ogni
misura sono stati pari a 600.000 [s], anche se sarebbe stato meglio aumentare i
tempi per misure a bassa tensione, in quanto il numero di coincidenze su tutti
e tre i rivelatori è decisamente basso a causa dell’insensibilità del rivelatore in
test sottoalimentato.
VH
2050±1
2100
2150
2200
2225
2250
2275
2300
2350
2400
2450
2500
2550
2600
ABC
21
63
150
252
272
321
395
453
466
545
540
508
511
525
σABC
5
8
12
16
16
18
20
21
22
23
23
23
23
23
BC
801
755
796
792
751
772
795
804
749
835
806
773
743
772
σBC
28
27
28
28
27
28
28
28
27
29
29
28
27
28
η
0.03
0.08
0.19
0.32
0.36
0.42
0.50
0.56
0.62
0.66
0.67
0.66
0.69
0.68
ση
0.01
0.01
0.02
0.02
0.03
0.03
0.03
0.03
0.04
0.04
0.04
0.04
0.04
0.04
Tabella 2.9: Misura dell’efficienza di A
2.6.3
Risultati
I calcoli statistici sono stati eseguiti direttamente sui conteggi, senza calcolare i rates, in quanto l’efficienza è data dal rapporto di grandezze che presentano entrambe dipendenza inversamente proporzionale al tempo di acquisizione
(Tacq = 600.000 ± 0.001[s]).
η=
ABC
BC
Sono stati plottati i valori delle efficienze in funzione della tensione di alimentazione del fotomoltiplicatore in esame (HVA ).
Dal grafico si ipotizza che possa esistere una relazione di diretta proporzionalità tra le due grandezze, almeno per una regione con valori di tensione minori
92
Rivelazione di raggi cosmici
Η
0.7
0.6
0.5
0.4
0.3
0.2
0.1
2100
2200
2300
2400
2500
2600
HV @VD
Figura 2.22: Rendimento di A
(in modulo) della tensione di saturazione del fotomoltiplicatore. Aumentando
la tensione oltre il punto di saturazione l’efficienza del device cresce meno rapidamente e può ritenersi costante. In questa zona, tuttavia aumenta il rumore
del fotomoltiplicatore e quindi può accadere che vengano conteggiati più eventi
(dovuti alla corrente di buio).
Sono stati eseguiti due fit lineari al fine di parametrizzare le due situazioni
rappresentate nel grafico (prima e dopo il punto di saturazione).
Tratto a derivata positiva
ρ = 0.996
a = 4.7 ± 0.2
b = 0.0023 ± 0.0001[V −1 ]
χ2 = 0.33
DF = 6 → χ2critico = 2
Punti dopo la saturazione
ρ = 0.87
a = 0.1 ± 0.4
b = 0.002 ± 0.002[V −1 ]
χ2 = 0.12
DF = 4 → χ2critico = 2.4
Per il tratto oltre il punto di saturazione è stato verificato che l’efficienza è
pressoché costante (si confronta il coefficiente angolare della retta con 0, tramite
test normale): è quindi stata calcolata un’efficienza media, mediante una media
pesata.
b
= 1.2 < zc = 1.96η = (66 ± 2)%
z=
σb
2.6 Misura dell’efficienza di un rivelatore
93
Η
0.6
0.4
0.2
2000
2100
2200
2300
2400
2500
2600
HV @VD
Figura 2.23: Rendimento di A - interpolazione
È da notare che oltre il punto di staurazione l’efficienza è costante, mentre
osservando il rumore di fondo tramite un oscilloscopio, questa grandezza aumenta all’aumentare del guadagno del fotomoltiplicatore. È quindi conveniente
operare in condizioni di massima efficienza, ma minimo rumore: tali condizioni
si hanno in un intorno del primo punto della retta orizzontale.
94
Rivelazione di raggi cosmici
Elenco delle tabelle
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.19
1.20
1.21
1.22
1.23
1.24
Uniformità del campo tra le espansioni del magnete
Ciclo di isteresi 1 . . . . . . . . . . . . . . . . . . . .
Ciclo d’isteresi 2 . . . . . . . . . . . . . . . . . . . .
Ciclo d’isteresi 3 . . . . . . . . . . . . . . . . . . . .
Germanio tipo N: Ib 1.600 ± 0.001 A . . . . . . . . .
Germanio tipo N: Ib 1.300 ± 0.001 A . . . . . . . . .
Germanio tipo N: Ib 1.000 ± 0.001 A . . . . . . . . .
Germanio tipo N: Ib 0.700 ± 0.001 A . . . . . . . . .
Germanio tipo N: Ib 0.393 ± 0.001 A . . . . . . . . .
Germanio tipo N: Ib 0.097 ± 0.001 A . . . . . . . . .
Germanio tipo N: Ib -0.405 ± 0.001 A . . . . . . . .
Germanio tipo N: Ib -0.700 ± 0.001 A . . . . . . . .
Germanio tipo N: Ib -1.000 ± 0.001 A . . . . . . . .
Germanio tipo N: Ib -1.299 ± 0.001 A . . . . . . . .
Germanio tipo N: Ib -1.602 ± 0.001 A . . . . . . . .
Germanio tipo N: RH calcolati dai fit lineari . . . . .
Germanio tipo P . . . . . . . . . . . . . . . . . . . .
Germanio tipo P . . . . . . . . . . . . . . . . . . . .
Germanio tipo P . . . . . . . . . . . . . . . . . . . .
Germanio tipo P . . . . . . . . . . . . . . . . . . . .
Germanio tipo P: RH calcolati dai fit lineari . . . . .
Salita . . . . . . . . . . . . . . . . . . . . . . . . . .
Discesa . . . . . . . . . . . . . . . . . . . . . . . . .
riSalita . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
13
16
16
17
24
24
24
24
25
25
25
25
26
26
26
34
35
36
36
36
42
47
47
47
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
Misura di eventi al variare di HV - ∆T = 100.000s . .
Misura di eventi sui singoli rivelatori - ∆T = 100.000s
Misura della curva di coincidenza sperimentale - rates
Rate di eventi singoli - ∆T = 100.000s . . . . . . . . .
Misura della curva di coincidenza sperimentale . . . .
Misura della curva di coincidenza sperimentale - rates
Misura di eventi accidentali . . . . . . . . . . . . . . .
Rates di eventi accidentali . . . . . . . . . . . . . . . .
Misura dell’efficienza di A . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
77
77
78
78
84
84
88
88
91
95
96
ELENCO DELLE TABELLE
Elenco delle figure
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.19
1.20
1.21
1.22
1.23
1.24
1.25
1.26
1.27
1.28
1.29
1.30
1.31
1.32
1.33
1.34
1.35
1.36
1.37
1.38
Semiconduttori intrinseci e drogati: configurazione elettronica . .
3
Effetto Hall con portatori di carica ± . . . . . . . . . . . . . . . .
5
Effetto Peltier . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
Effetto Seeback . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
Elettromagnete . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Andamento del campo magnetico tra le espansioni del magnete . 14
Andamento del campo magnetico tra le espansioni del magnete . 14
Setup sperimentale: misura del ciclo di isteresi magnetica del traferro 15
Primo ciclo di isteresi: dati raccolti nelle misure sperimentali . . 17
Secondo ciclo di isteresi: dati raccolti nelle misure sperimentali . 20
Terzo ciclo di isteresi: dati raccolti nelle misure sperimentali . . . 20
Retta di calibrazione finale B = B(IB ) . . . . . . . . . . . . . . . 22
Setup sperimentale: misura dell’effetto Hall . . . . . . . . . . . . 22
Germanio tipo N: prima serie di dati, Ib 1.600 A . . . . . . . . . 27
Germanio tipo N: seconda serie di dati, Ib 1.300 A . . . . . . . . 27
Germanio tipo N: terza serie di dati, Ib 1.000 A . . . . . . . . . . 28
Germanio tipo N: quarta serie di dati, Ib 0.701 A . . . . . . . . . 29
Germanio tipo N: quinta serie di dati, Ib 0.393 A . . . . . . . . . 29
Germanio tipo N: sesta serie di dati, Ib 0.097 A . . . . . . . . . . 30
Germanio tipo N: settima serie di dati, Ib -0.405 A . . . . . . . . 31
Germanio tipo N: ottava serie di dati, Ib -0.700 A . . . . . . . . . 31
Germanio tipo N: nona serie di dati, Ib -1.000 A . . . . . . . . . 32
Germanio tipo N: decima serie di dati, Ib -1.299 A . . . . . . . . 33
Germanio tipo N: undicesima serie di dati, Ib -1.602 A . . . . . . 33
Germanio tipo N: valori del coefficiente di Hall in funzione del campo 34
Germanio tipo P: prima serie di dati, Ib 1.599 A . . . . . . . . . 37
Germanio tipo P: seconda serie di dati, Ib 1.300 A . . . . . . . . 38
Germanio tipo P: terza serie di dati, Ib 1.000 A . . . . . . . . . . 38
Germanio tipo P: quarta serie di dati, Ib 0.501 A . . . . . . . . . 39
Germanio tipo P: quinta serie di dati, Ib -0.501 A . . . . . . . . . 40
Germanio tipo P: sesta serie di dati, Ib -1.000 A . . . . . . . . . 40
Germanio tipo P: settima serie di dati, Ib -1.300 A . . . . . . . . 41
Germanio tipo P: ottava serie di dati, Ib -1.600 A . . . . . . . . . 42
Germanio tipo N: valori del coefficiente di Hall in funzione del campo 43
Setup sperimentale: misura della resistività di un semiconduttore 45
Relazione T (V ) per la termocoppia . . . . . . . . . . . . . . . . . 48
Dati raccolti: prima salita, discesa e risalita . . . . . . . . . . . . 49
Prima serie di dati: salita, R(T ) . . . . . . . . . . . . . . . . . . 49
97
98
ELENCO DELLE FIGURE
1.39
1.40
1.41
1.42
1.43
1.44
1.45
Seconda serie di dati: discesa, R(T ) . . . . . . . . . . . . . . . . 50
Terza serie di dati: risalita, R(T ) . . . . . . . . . . . . . . . . . . 50
Prima serie: Log(R) in funzione di Log(T ), punti sperimentali e retta interpolatrice 51
Seconda serie: Log(R) in funzione di Log(T ), punti sperimentali e retta interpolatrice 52
Terza serie: Log(R) in funzione di Log(T ), punti sperimentali e retta interpolatrice 52
Prima serie: Log(R) in funzione di 1/T , punti sperimentali e retta interpolatrice 53
Seconda serie: Log(R) in funzione di 1/T , punti sperimentali e retta interpolatrice 54
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2.16
2.17
2.18
2.19
2.20
2.21
2.22
2.23
Possibili decadimenti di un raggio cosmico . . . . . . . . . . . . . 58
Schema di uno scintillatore . . . . . . . . . . . . . . . . . . . . . 59
Decadimento di elettroni e fluorescenza in una molecola organica 62
Sezione di un fotomoltiplicatore . . . . . . . . . . . . . . . . . . . 64
Schema elettrico del voltage divider . . . . . . . . . . . . . . . . . 67
Schema delle coincidenze . . . . . . . . . . . . . . . . . . . . . . . 71
Rivelatori di particelle: scintillatori e fotomoltiplicatori . . . . . . 72
Risposta del rivelatore A per un cosmico incidente . . . . . . . . 73
Risposta del rivelatore B per un cosmico incidente . . . . . . . . 74
Risposta del rivelatore C per un cosmico incidente . . . . . . . . 74
Setup sperimentale: misura della HV . . . . . . . . . . . . . . . 75
Rates misurati da A in funzione di HV . . . . . . . . . . . . . . . 79
Rates misurati da B in funzione di HV . . . . . . . . . . . . . . . 79
Rates misurati da C in funzione di HV . . . . . . . . . . . . . . . 80
Disposizione dei rivelatori per la determinazione della curva di coincidenza 82
Setup sperimentale: misura della curva di coincidenza . . . . . . 83
Coincidenze in funzione del ritardo . . . . . . . . . . . . . . . . . 85
Coincidenze in funzione del ritardo - rette . . . . . . . . . . . . . 86
Visualizzazione del delay massimo . . . . . . . . . . . . . . . . . 88
Disposizione dei rivelatori per la misura di efficienza . . . . . . . 89
Setup sperimentale: misura di efficienza . . . . . . . . . . . . . . 90
Rendimento di A . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
Rendimento di A - interpolazione . . . . . . . . . . . . . . . . . . 93