Poligoni
Def:
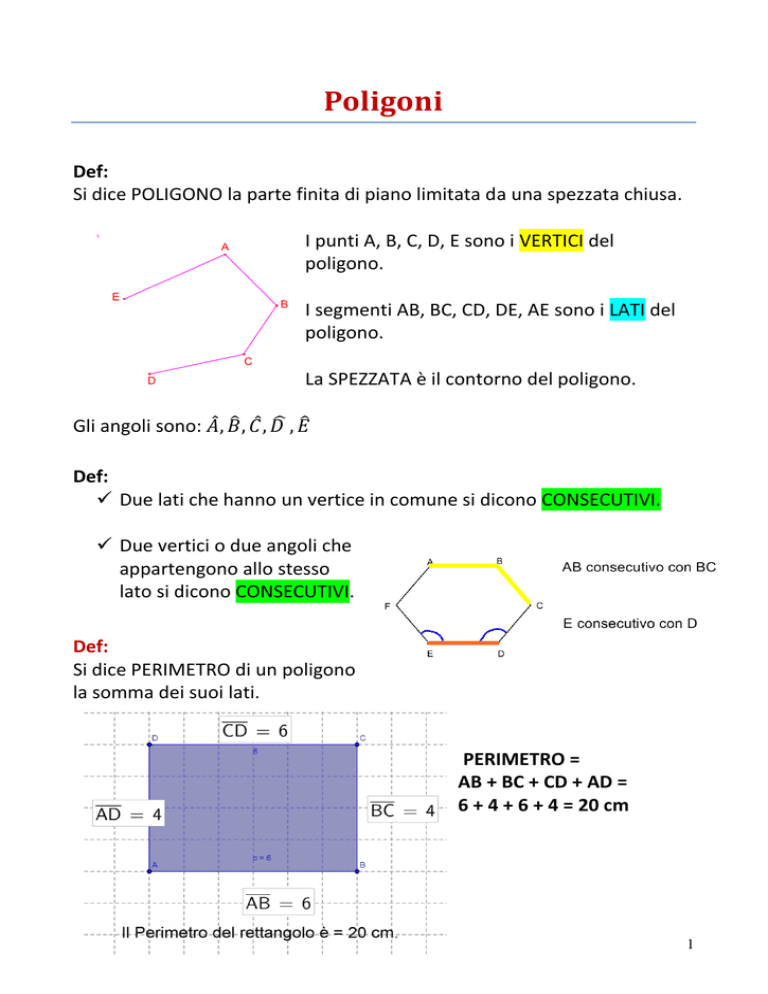
Si dice POLIGONO la parte finita di piano limitata da una spezzata chiusa.
I punti A, B, C, D, E sono i VERTICI del
poligono.
A
E
B
I segmenti AB, BC, CD, DE, AE sono i LATI del
poligono.
C
D
La SPEZZATA è il contorno del poligono.
Gli angoli sono: ̂ ̂ ̂ ̂ ̂
Def:
Due lati che hanno un vertice in comune si dicono CONSECUTIVI.
Due vertici o due angoli che
appartengono allo stesso
lato si dicono CONSECUTIVI.
Def:
Si dice PERIMETRO di un poligono
la somma dei suoi lati.
PERIMETRO =
AB + BC + CD + AD =
6 + 4 + 6 + 4 = 20 cm
1
Proprietà:
Un poligono si dice CONVESSO se si trova tutto in uno stesso semipiano
rispetto a ciascuna delle rette cui appartiene un suo lato;
si dice CONCAVO se è attraversato da una o più rette alle quali appartiene
un suo lato.
Def:
ANGOLO INTERNO: ciascun angolo di un poligono formato da due
lati consecutivi;
ANGOLO ESTERNO: ogni angolo adiacente ad un angolo interno di
un poligono.
2
OSSERVAZIONI:
1. l’angolo esterno è formato dal prolungamento di uno dei lati che
delimitano l’angolo interno;
2. ogni angolo interno ha due angoli esterni tra loro congruenti
(OPPOSTI AL VERTICE);
3. angolo interno e angolo esterno sono SUPPLEMENTARI, la loro
somma è un angolo PIATTO (
).
DENOMINAZIONE DEI POLIGONI
Proprietà:
Un poligono ha almeno 3 lati, 3 angoli e 3 vertici.
Un poligono prende il nome dal numero dei suoi lati o dei suoi
angoli.
TRIANGOLO: 3 lati, 3 angoli e 3 vertici.
QUADRILATERO: 4 lati, 4 angoli e 4 vertici.
3
PENTAGONO: 5 lati, 5 angoli e 5 vertici.
ESAGONO: 6 lati, 6 angoli e 6 vertici.
ETTAGONO: 7 lati, 7 angoli e 7 vertici.
OTTAGONO: 8 lati, 8 angoli e 8 vertici.
4
Def:
Un poligono si dice EQUILATERO se ha tutti i lati congruenti.
ROMBO
Def:
Un poligono si dice EQUIANGOLO se tutti gli angoli sono congruenti.
RETTANGOLO
Def:
Un poligono si dice REGOLARE se è equilatero ed equiangolo e cioè se ha
tutti i lati e tutti gli angoli congruenti.
ROMBO non è regolare, perché ha i lati uguali , ma gli angoli no.
RETTANGOLO non è regolare, perché ha gli angoli uguali, ma i lati
no.
QUADRATO è REGOLARE.
Tutti i poligoni che sono regolari, nel nome si aggiunge la parola
“REGOLARE”: ESAGONO REGOLARE, PENTAGONO REGOLARE, OTTAGONO
REGOLARE….
5
PENTAGONO REGOLARE
Proprietà:
Ciascun lato di un poligono è minore della somma di tutti gli altri lati.
Def:
Si dice DIAGONALE di un poligono ogni segmento che unisce due suoi
vertici non consecutivi.
6
Regola:
per calcolare il numero delle diagonali di un poligono si applica la
seguente formula
[
(
)]
n = numero lati
TRIANGOLO : n = 3
[
(
[
)]
]
QUADRILATERO : n = 4
[
(
)]
[
]
PENTAGONO : n
=5
[
(
)]
[
ESAGONO:
[
(
)]
]
n =6
[
]
Regola:
per calcolare il numero delle diagonali uscenti da un vertice di un
poligono si applica la seguente formula:
n = numero il dei lati.
Esempio:Esagono:
da ogni vertice partono 3 diagonali
7
Teorema 1
La somma degli angoli interni di un triangolo è uguale a
1800 .
Teorema 2
In ogni triangolo, un angolo esterno è congruente alla somma dei due
angoli interni ad esso non adiacenti.
̂
8
Teorema 3
La somma degli angoli interni di un poligono di n lati è:
Si (n2)1800
n = numero dei lati del poligono.
Es:
TRIANGOLO:
(
)
(
)
QUADRILATERI:
(
)
(
)
PENTAGONO:
(
)
(
)
ESAGONO:
(
)
(
)
Teorema 4
la somma degli angoli interni e degli angoli esterni di un poligono di n lati
è:
= somma totale angoli interni e esterni
TRIANGOLO:
QUADRILATERI:
9
PENTAGONO:
(dimostrazione solo da leggere e capire sul libro pag. 138)
Teorema 5
la somma degli angoli esterni di un poligono qualsiasi è:
Se 3600 ( qualunque sia il numero dei lati)
(no dimostrazione)
RIEPILOGO
SOMMA ANGOLI INTERNI
(
)
SOMMA ANGOLI ESTERNI
SOMMA TOTALE ANGOLI
(interni più esterni)
10











