27-09-2012
9:58
Pagina 1
B1 • Metodi di risoluzione delle reti lineari
Esercizi aggiuntivi – Unità B1
Esercizi svolti
Esercizio 1
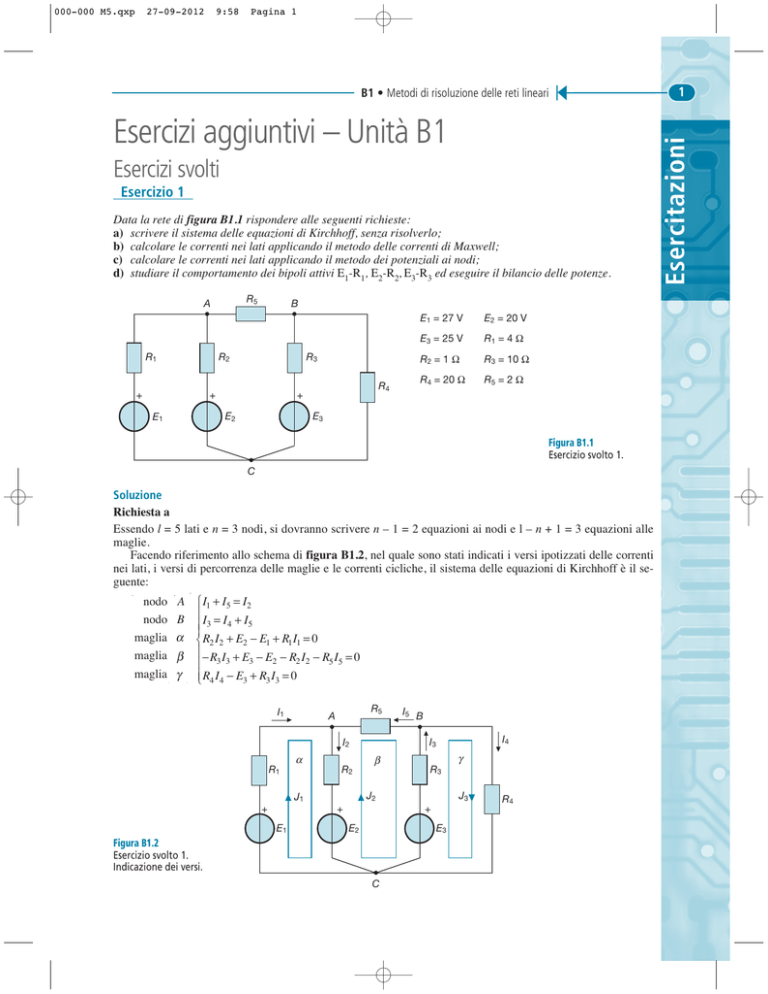
Data la rete di figura B1.1 rispondere alle seguenti richieste:
a) scrivere il sistema delle equazioni di Kirchhoff, senza risolverlo;
b) calcolare le correnti nei lati applicando il metodo delle correnti di Maxwell;
c) calcolare le correnti nei lati applicando il metodo dei potenziali ai nodi;
d) studiare il comportamento dei bipoli attivi E1-R1, E2-R2, E3-R3 ed eseguire il bilancio delle potenze.
R5
A
B
R2
R1
R3
+
+
E2 = 20 V
E3 = 25 V
R1 = 4 Ω
R2 = 1 Ω
R3 = 10 Ω
R4 = 20 Ω
R5 = 2 Ω
E3
E2
E1
R4
+
E1 = 27 V
Figura B1.1
Esercizio svolto 1.
C
Soluzione
Richiesta a
Essendo l = 5 lati e n = 3 nodi, si dovranno scrivere n – 1 = 2 equazioni ai nodi e l – n + 1 = 3 equazioni alle
maglie.
Facendo riferimento allo schema di figura B1.2, nel quale sono stati indicati i versi ipotizzati delle correnti
nei lati, i versi di percorrenza delle maglie e le correnti cicliche, il sistema delle equazioni di Kirchhoff è il seguente:
nodo
nodo
maglia
maglia
maglia
A
B
α
β
γ
⎧ I1 + I5 = I2
⎪
⎪ I3 = I 4 + I 5
⎪
⎨ R2 I2 + E2 − E1 + R1 I1 = 0
⎪− R I + E − E − R I − R I = 0
3
2
2 2
5 5
⎪ 3 3
⎪⎩ R4 I4 − E3 + R3 I3 = 0
I1
R5
A
I2
R1
α
R2
β
+
E1
I4
I3
R3
J2
J1
+
I5 B
J3
+
E2
E3
Figura B1.2
Esercizio svolto 1.
Indicazione dei versi.
C
γ
R4
1
Esercitazioni
000-000 M5.qxp
000-000 M5.qxp
27-09-2012
9:58
Pagina 2
Esercitazioni
2
Modulo B • Risoluzione delle reti elettriche lineari in corrente continua
Richiesta b
L’applicazione del metodo di Maxwell richiede la risoluzione di un sistema costituito da l – n + 1 = 3 equazioni.
Indicando con J1, J2, J3 le tre correnti cicliche e scrivendo le equazioni relative alle tre maglie, si ottiene:
− E1 + R1 J1 + R2 ( J1 − J2 ) + E2 = 0
R3 ( J2 − J3 ) + E3 − E2 + R2 ( J2 − J1 ) + R5 J2 = 0
R4 J3 − E3 + R3 ( J3 − J2 ) = 0
Sostituendo i valori noti e semplificando, si ha:
⎧−27 + 4 J1 + J1 − J2 + 20 = 0
⎪
⎨10 J2 − 10 J3 + 25 − 20 + J2 − J1 + 2 J2 = 0
⎪20 J − 25 + 10 J − 10 J = 0
3
3
2
⎩
⎧−7 + 5 J1 − J2 = 0
⎪
⎨5 − J1 + 13 J2 − 10 J3 = 0
⎪−25 − 10 J + 30 J = 0
2
3
⎩
⎧−7 + 5 J1 − J2 = 0
⎪
⎨5 − J1 + 13 J2 − 10 J3 = 0
⎪−5 − 2 J + 6 J = 0
2
3
⎩
Se si ricavano J1 dalla prima e J3 dalla terza equazione, entrambe soltanto in funzione di J2, e si sostituiscono
nella seconda equazione, si ottiene un’unica espressione con incognita J2. Eseguendo i vari calcoli, si ha:
J1 =
5−
7 + J2
5
J3 =
5 + 2 J2
6
7 + J2
5 + 2 J2
+ 13 J2 − 10
=0
5
6
J2 =
71
= 0, 5 A
142
J1 =
−71 + 142 J2 = 0
7 + 0, 5
= 1, 5 A
5
J3 =
5 + 2 × 0, 5
=1 A
6
Il calcolo delle correnti nei lati, in funzione di quelle di maglia, è immediato se si osservano i versi indicati
nella figura B1.2:
I1 = J1
I1 = 1, 5 A
I2 = J1 − J2
I 4 = J3
I4 = 1 A
I5 = − J 2
I2 = 1 A
I3 = J 3 − J 2
I3 = 0, 5 A
I5 = −0, 5 A
Il segno negativo della corrente I5 indica che il verso è opposto a quello ipotizzato e quindi la corrente effettiva va dal nodo A al nodo B.
Richiesta c
L’applicazione del metodo dei potenziali ai nodi richiede la risoluzione di un sistema di n – 1 = 2 equazioni e,
quindi, tale metodo risulta il più conveniente per la rete in esame.
Prendendo C come nodo di riferimento a potenziale zero si ha:
nodo A: E1G1 + E2 G2 = VA (G1 + G2 + G5 ) − VB G5
nodo B: E3G3 = VB (G3 + G4 + G5 ) − VA G5
Sostituendo i valori noti e semplificando, si ottiene il sistema:
⎧ 27 20
⎛ 1 1 1⎞ 1
⎪⎪ 4 + 1 = VA ⎝ 4 + 1 + 2 ⎠ − 2 VB
⎨
⎪ 25 = V ⎛ 1 + 1 + 1 ⎞ − 1 V
B
⎝ 10 20 2 ⎠ 2 A
⎪⎩ 10
27-09-2012
9:58
Pagina 3
B1 • Metodi di risoluzione delle reti lineari
⎧26, 75 = 1, 75 VA − 0, 5 VB
⎨
⎩2, 5 = 0, 65 VB − 0, 5 VA
Risolvendo il sistema precedente (si omettono, per brevità, i passaggi matematici), si calcolano i potenziali
dei nodi A e B e le d.d.p. tra le coppie di nodi:
VA = 21 V
VB = 20 V
VAC = VA − VC = 21 − 0 = 21 V
VAB = VA − VB = 21 − 20 = 1 V
VBC = VB − VC = 20 − 0 = 20 V
Dalle equazioni caratteristiche dei vari lati (legge di Ohm generalizzata) si ottengono le correnti:
VAC = − R1 I1 + E1
VAC = R2 I2 + E2
VBC = − R3 I3 + E3
VBC = R4 I4
VAB = − R5 I5
I4 =
I1 =
I2 =
E1 − VAC 27 − 21
=
= 1, 5 A
R1
4
VAC − E2 21 − 20
=
=1 A
R2
1
I3 =
E3 − VBC 25 − 20
=
= 0, 5 A
R3
10
VBC 20
=
=1 A
R4 20
I5 = −
VAB
1
= − = − 0, 5 A
R5
2
valori che confermano quelli calcolati al punto b.
Richiesta d
Dall’esame dei risultati ottenuti si deduce che:
•
•
•
il bipolo attivo E1-R1 si comporta da generatore, essendo E1 > VAC
il bipolo attivo E2-R2 si comporta da utilizzatore attivo, essendo E2 < VAC
il bipolo attivo E3-R3 si comporta da generatore, essendo E3 > VBC
Per applicare la formula del bilancio delle potenze occorre calcolare le potenze utili dei generatori, la potenza
assorbita dall’utilizzatore attivo e quelle assorbite dai resistori R4 e R5:
Pu1 = VAC I1 = 21 × 1, 5 = 31, 5 W
PR4 = R4 I42 = 20 × 12 = 20 W
Pu3 = VBC I3 = 20 × 0, 5 = 10 W
PR5 = R5 I52 = 2 × 0, 52 = 0, 5 W
Pa 2 = VAC I2 = 21 × 1 = 21 W
Eseguendo il bilancio delle potenze, si ottiene:
Pu1 + Pu3 = PR 4 + PR5 + Pa 2
31, 5 + 10 = 20 + 0, 5 + 21 41, 5 W = 41,5 W
Esercizio 2
Per la rete di figura B1.1 dell’esercizio 1 calcolare la corrente nel resistore R5 mediante il metodo del generatore
equivalente di Thevenin.
3
Esercitazioni
000-000 M5.qxp
000-000 M5.qxp
27-09-2012
9:58
Pagina 4
Esercitazioni
4
Modulo B • Risoluzione delle reti elettriche lineari in corrente continua
Soluzione
Interrompendo la rete tra i nodi A e B e disattivando i tre bipoli attivi di tensione si ottiene il circuito di figura
B1.3, la cui resistenza totale è quella del generatore equivalente:
RTh = R1 // R2 + R3 // R4 =
4 × 1 10 × 20
+
= 7, 47 Ω
4 + 1 10 + 20
RTh
A
B
R1
R2
R3
R4
Figura B1.3
Esercizio svolto 2.
Circuito per il calcolo di RTh.
C
La f.e.m. del generatore equivalente corrisponde alla tensione a vuoto tra i morsetti A e B del circuito di figura B1.4, comprendente due maglie tra loro separate, percorse dalle correnti I′ e I′′, per il calcolo delle quali basta scrivere le relative equazioni di Kirchhoff:
R2 I ′ + E2 − E1 + R1 I ′ = 0
I ′ ( R1 + R2 ) = E1 − E2
I′ =
E1 − E2 27 − 20
= 1, 4 A
=
R1 + R2
4 +1
R4 I ′′ − E3 + R3 I ′′ = 0
I ′′ ( R3 + R4 ) = E3
I ′′ =
E3
25
=
= 0, 833 A
R3 + R4 10 + 20
A
I′
ETh = V0
B
I′
I′′
R3
R2
R1
+
+
E1
I′′
R4
+
E2
E3
Figura B1.4
Esercizio svolto 2.
Circuito per il calcolo di ETh.
C
Seguendo uno dei possibili percorsi tra i punti A e B si ricava la tensione cercata:
ETh = V0 = R2 I ′ + E2 − R4 I ′′ = 1 × 1, 4 + 20 − 20 × 0, 833 = 4, 74 V
Il circuito equivalente ottenuto è rappresentato nella figura B1.5.
La corrente incognita è data da:
I5 =
A
+
I5
ETh
ETh
4, 74
=
= 0, 5 A
RTh + R5 7, 47 + 2
R5
Figura B1.5
Esercizio svolto 2.
Circuito equivalente.
RTh
B
000-000 M5.qxp
27-09-2012
9:58
Pagina 5
B1 • Metodi di risoluzione delle reti lineari
5
Per la rete di figura B1.6 calcolare la tensione VBH e la corrente I1 applicando il teorema di Millmann. Ripetere
il calcolo di I1 mediante la sovrapposizione degli effetti. Calcolare, inoltre, le tensioni su ognuno dei due bipoli
del lato centrale.
R1
A
R2
B
C
+ 10 V
+5V
I1
I03
I03 = 50 mA
R1 = 200 Ω
R2 = 75 Ω
R3 = 100 Ω
K
R3
Figura B1.6
Esercizio svolto 3.
H
Soluzione
Dato che i punti A e C hanno, rispettivamente, potenziali di + 10 V e + 5 V rispetto a massa (punto H) è come se
ci fossero due generatori ideali di tensione, con f.e.m. E1 = 10 V tra A e H e f.e.m. E2 = 5 V tra B e H.
Rappresentando i due bipoli si ottiene lo schema di figura B1.7.
A
R1
R2
B
+
I03
C
+
E2 = 5 V
E1 =10 V
K
VR3
R3
H
Figura B1.7
Esercizio svolto 3.
Schema con i generatori
di tensione.
La presenza del resistore R3 nel lato centrale, in serie al generatore di corrente, non modifica l’applicazione
del teorema di Millmann per il calcolo di VBH, dato che non influisce sulla corrente I03 impressa nel lato. Tale presenza modificherà soltanto la suddivisione della d.d.p. lungo il lato in oggetto.
Applicando, quindi, il teorema di Millmann senza considerare R3 si ottiene:
VBH
E1
E
5
10
+ I03 + 2
+ 0,05 +
R1
R2
75 = 9,1 V
=
= 200
1
1
1
1
+
+
R1 R2
200 75
Essendo VBH < E1, il bipolo di sinistra funzionerà da generatore e la corrente sarà data da:
I1 =
E1 − VBH 10 − 9,1
=
= 0, 0045 A = 4,5 mA
R1
200
Esercitazioni
Esercizio 3
000-000 M5.qxp
27-09-2012
9:58
Esercitazioni
6
Pagina 6
Modulo B • Risoluzione delle reti elettriche lineari in corrente continua
Per applicare la sovrapposizione degli effetti bisogna considerare l’azione di un bipolo attivo per volta, disattivando gli altri due: si ottengono i circuiti rappresentati nella figura B1.8 a, b, c, per i quali è immediato il calcolo dei vari contributi:
I1′ =
10
E1
=
= 0, 0363 A = 36, 3 mA
R1 + R2 200 + 75
I1′′′=
5
E2
=
= 0, 0182 A =18,2 mA
R1 + R2 200 + 75
R1
+
B
I1′′= I03
R2
75
= 50
= 13, 6 mA
R1 + R2
200 + 75
R1
R2
R2
B
I′′1
I ′1
I03
E1
a)
R3
H
b)
H
R1
B
R2
I′′′1
+
E2
c)
H
Figura B1.8
Esercizio svolto 3.
Applicazione della
sovrapposizione degli effetti.
La corrente I1, diretta da A verso B, è la somma algebrica dei tre contributi:
I1 = I1′ − I1′′− I1′′′= 36, 3 − 13, 6 − 18, 2 = 4, 5 mA
e il suo valore coincide con quello ottenuto mediante l’applicazione del teorema di Millmann.
Per rispondere all’ultima domanda occorre ragionare sui potenziali dei vari punti e sulle loro differenze, ottenendo:
VHK = VR3 = R3 I3 = 100 × 50 × 10 −3 = 5 V
VBH = VBK − VR3 ; VBK = VBH + VR3 = 9,1 + 5 = 14,1 V
VKH = VK − VH ; VK = VKH + VH = −VR3 + 0 = −5 V
Si può osservare che il potenziale del punto K è negativo rispetto alla massa (– 5 V): questo è l’effetto del resistore R3, in assenza del quale K sarebbe coinciso con la massa e la tensione sul generatore di corrente sarebbe stata
pari a 9,1 V e non 14,1 V.
Esercizi proposti
Esercizio 4
Per la rete di figura B1.9 calcolare la corrente nel resistore R5 con i metodi dei generatori equivalenti di Norton
e di Thevenin e con la sovrapposizione degli effetti.
000-000 M5.qxp
27-09-2012
9:58
Pagina 7
7
B1 • Metodi di risoluzione delle reti lineari
R2
R3
I06
+
C
R2 = 20 Ω
R3 = 40 Ω
R4 = 50 Ω
R5 = 10 Ω
I06 = 2 A
E1
D
R5
E1 = 20 V
R4
Figura B1.9
Esercizio proposto 4.
B
[I5 = 1,2 A da B verso C]
Esercizio 5
Per la rete di figura B1.10calcolare le tensioni VAB e Vu (tensione d’uscita). Calcolare inoltre il valore che dovrebbe assumere R3 per avere una tensione d’uscita Vu = – 2 V.
R4
A
R1
E2
I1
+
+
B
R2
I2
Vu
R5
E1 = 0,5 V
R1 = 1,2 kΩ
R2 = 1,8 kΩ
R3 = 2 kΩ
R4 = 6,8 kΩ
R5 = 1,2 kΩ
E2 = 100 VA
R3
E1
Figura B1.10
Esercizio proposto 5.
H
Ω]
[VAB = –5,7 V; Vu = –3,6 V; R3 = 10 kΩ
Esercizio 6
Per la rete di figura B1.11 calcolare la f.e.m. E1 in modo che sia VB = 8 V. In tali condizioni di funzionamento
calcolare la tensione d’uscita Vu e la resistenza d’ingresso Ri. Applicando il teorema di Miller delle correnti trasformare il circuito e verificare che Vu e Ri non siano variate.
I
C
IR2
R1
I2
R3
Ri
+
E1
I1
A
B
R5
R2
I4
Vu
R1 = 1 kΩ
R2 = 5 kΩ
R3 = 1,2 kΩ
R4 = 0,8 kΩ
R5 = 2,2 kΩ
I2 = 49 I1
R4
H
Figura B1.11
Esercizio proposto 6.
Ω]
[E1 = 10 V; Vu = –21,56 V; Ri = 4,46 kΩ
Esercitazioni
A