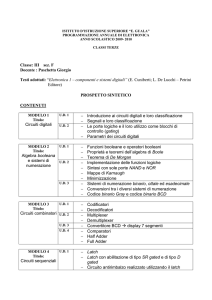
Decimazione in frequenza (Decimation in frequency)
Si può pensare di derivare direttamente un algoritmo FFT di decimazione
nel dominio della frequenza, invece di fare una trasposizione di un
algoritmo dato di decimazione nel tempo.
A tale scopo si divide la sequenza in due metà e si definiscono le
sequenze somma e differenza di lunghezza N/2 attraverso:
~
f ( n) = ~
x ( n) + ~
x ( n + N / 2)
e
g~ ( n) = ~
x ( n) − ~
x ( n + N / 2)
per n = 0, 1, . . . , (N/2) - 1.
M. Usai
Circuiti digitali 7_5
(7.4.5)
1
Valutando la DFT a N/2 punti si ha:
~
F (l ) =
( N / 2 ) −1
∑
~
f (n)(W 2 ) ln ,
n=0
( N / 2 ) −1
=
∑
( N / 2 ) −1
~
x (n)W 2 ln +
n=0
n=0
( N / 2 ) −1
=
∑
n=0
∑
~
x (n + N / 2)W 2 ln
~
x (n)W 2 ln +
N −1
∑
n= N / 2
~
x (n)W 2 ln
l = 0, 1,. . . , (N/2) - 1,
(7.4.6)
dove si è trascurato il fattore W-2l(N/2) dall’ultima sommatoria in (7.4.2) poiché
WlN è uguale all’unità per tutti i valori di l.
M. Usai
Circuiti digitali 7_5
2
Quindi:
~
F (l ) =
N −11
∑
~
~
x (n)W 2 ln = X (2l ), l = 0, 1, . . . , (N/2) - 1
(7.4.7)
n =0
cioè da i campioni numerati pari della DFT. Comunque se si valuta la DFT di
ordine N/2 punti della sequenza delle differenze modulate , si ottiene:
~
Gm (l ) =
( N / 2 ) −1
∑
W n g~ (n)(W 2 ) ln ,
n =0
=
=
( N / 2 ) −1
( N / 2 ) −1
n=0
( N / 2 ) −1
n=0
∑
∑
n=0
~
x (n)W ( 2l +1) n −
~
x (n)W ( 2l +1) n +
∑
~
x (n + N / 2)W ( 2l +1) n
N −1
∑
~
x (n)W ( 2l +1) n
l = 0, 1,. . . , (N/2) - 1,
n= N / 2
(7.4.8)
dove si è sostituito il fattore W-(2l+1)(N/2) con il suo valore(-1) nell’ultima
sommatoria in (7.4.8).
M. Usai
Circuiti digitali 7_5
3
Quindi:
~
G (l ) =
N −1
∑
~
( 2l +1) n
~
x (n)W
= X (2l + 1),
l = 0, 1, . . . , (N/2) - 1,
n=0
cioè da i campioni numerati dispari di . I fattori di modulazione Wn nella
sequenza W n g~ (n) sono fattori di rotazione nell’algoritmo.
Come nel caso dell’algoritmo della decimazione nel tempo, questo concetto
viene applicato di seguito più volte sino a quando si ha solamente da
valutare la DFT di ordine 2.
Cioè le sequenza a N/2 punti e vengono divise ciascuna in due sequenze di
N/4 punti, essendo modulate le ultime due metà con W2n e così via per r
stadi dove N=2r. L’algoritmo risultante della decimazione in frequenza
corrisponde alla figura 7.17, ma con l’incorporazione della farfalla in figura
7.16
M. Usai
Circuiti digitali 7_5
4
Figura 7.16 Decimazione butterfly in frequenza con una sola moltiplicazione complessa.
M. Usai
Circuiti digitali 7_5
5
Figura 7.17 Diagramma della FFT con una decimazione in frequenza a 8 punti.
M. Usai
Circuiti digitali 7_5
6
In tabella 7.3 è riportato un programma FORTRAN per l’algoritmo FFT della
decimazione in frequenza
M. Usai
Circuiti digitali 7_5
7
Oltre alle possibilità precedentemente menzionate per calcolare
direttamente l’operatore Wqn=cos(2πqn/N)-j sin(2πqn/N) o definendolo
in una matrice predefinita,
una terza possibilità consiste nel calcolarlo ricorsivamente usando una
semplice equazione alle differenze
Wqn=WqWq(n-1)
(7.4.10)
per n=1, 2, 3, . . ..
M. Usai
Circuiti digitali 7_5
8
Il terzo metodo corrisponde alla quadratura (quadrature) dell’oscillatore
digitale dove si mostra che attualmente vengono richieste solo due
moltiplicazioni reali per ricorsione e non 4 come per una moltiplicazione
complessa arbitraria. Quindi gli errori cumulativi di quantizzazione risultanti
dall’uso ripetitivo di (7.4.10) causeranno eventualmente grandi errori nei
valori calcolati per Wqn, a meno che le condizioni iniziali per la ricorsione
vengano reimpostati periodicamente.
Una scelta ovvia per resettare Wqn si ha quando (qn)mod N =0 poiché W0=1.
M. Usai
Circuiti digitali 7_5
9
DFT inversa: IDFT
Potrebbe sembrare dalle definizioni della DFT in (7.1.4) e dalla DFT inversa
IDFT in (7.1.6) che potrebbero essere richiesti diverse forme di vari algoritmi
FFT per valutare la DFT e la IDFT.
Quindi coniugando la (7.1.6) si trova che :
1
~
x * ( n) =
N
N −1
∑
~
X * (k )W kn , n = 0, 1, ..., N - 1 (7.4.11)
k =0
Cioè la DFT della matrice ridotta di 1/N, da il coniugato della matrice di
output desiderata . Quindi si può usare l’algoritmo FFT per calcolare la DFT
inversa attraverso una prima coniugazione della matrice di input calcolando la
sua DFT e quindi coniugando la matrice di output risultante.
Certamente se la matrice di output ha valori reali, l’operazione di coniugazione
finale non è richiesta.
M. Usai
Circuiti digitali 7_5
10
Shuffling (mescolamento)
Come visto in precedenza per entrambi gli algoritmi della decimazione nel
tempo e della decimazione nella frequenza, sia la matrice dei dati di input che
di output saranno ordinati a bit rovesciati, se vengono impiegate le
configurazioni a farfalle in place.
Per molte applicazioni è quindi richiesto l’ordinamento o shuffling
(mescolamento) della matrice di bit rovesciati a partire dall’ordine naturale.
Se la FFT è implementata in hardware, è insignificante costruire un
contatore binario che conta i bit in ordine inverso- proprio invertire gli r
outputs bit da un contatore standard lineare binario 2r.
•
• Se quindi l’FFT deve essere implementata in software, contare in ordine
bit inverso, diventa talvolta più complesso.
M. Usai
Circuiti digitali 7_5
11
Robin e Gold danno un diagramma di flusso dovuto a Rader per questo
contatore a bit inverso [91] Per eseguire un ordinamento (sorting) alla matrice
degli output dall’algoritmo della decimazione in frequenza, si devono
~
%
X
(
k
)
X
scambiare
e (k ' ) , dove k’ è l’indice nell’ordine naturale.
~
~
Per esempio in fig. 7.17, dobbiamo scambiare e X (4) con X (3)
.
Quando k=k’, ovviamente, non
è necessario alcuno scambio altrimenti devono
~
essere scambiati X% (k ) con X (k ' ) . Per essere sicuri che lo scambio è fatto
solamente una volta, fare lo scambio solo se k>k’ (o viceversa).
M. Usai
Circuiti digitali 7_5
12
Quindi l’algoritmo completo di sorting richiede una implementazione di un
contatore (k’) in ordine naturale,
un altro contatore in ordine bit-inverso e
~
lo scambio di X% (k ) con X (k ' ) ogni qualvolta che k > k’.
In alcune applicazioni della FFT l’ordinamento(sorting) di dall’ordine bitinverso all’ordine naturale non è richiesto.
~
~
~
Per esempio se la convoluzione
y
(
n
)
=
x
(
n
)
*
h
( n) è stata implementata
~
~
calcolando la DFT X (k ) e H ' (k ) , quindi moltiplicandole per
ottenere
~
~
~
~
inversa Y (k ) per
Y ( k ) = X (k ) H (k ) e infine~facendo~ la trasformata
~
determinare ~
y ( k ) , allora X (k ) , Y (k ) e H (k ) possono rimanere tutte
in ordine inverso.
~
Così per esempio X~ (k ) e H
(k ) possono essere valutate attraverso
~
~
h
l’algoritmo della decimazione di frequenza
da e x ( k ) e (k ) in ordine
~
~
naturale e y (n) può essere calcolato da Y (k ) usando l’algoritmo della
decimazione nel tempo, eccetto per la matrice input a bit inverso.
M. Usai
Circuiti digitali 7_5
13
~
Viceversa , se la funzione di autocorrelazione r (n) è stata valutata come
2
la DFT inversa della S~ (k ) = X~ (k~) / N , come descritto nel paragrafo
7.6 , allora non è necessario che X (k ) sia in ordine naturale.
FFT a radice 4 ( Radix-4 FFT)
Tutti gli algoritmi FFT precedenti sono basati su valutazioni a farfalla di
2 input e 2 output e sono classificati come algoritmi a radice 2 (radix-2).
Possono essere usati altri valori di radice intera n per sviluppare gli
algoritmi FFT.
Per esempio nella prima derivazione di ordine 8 della decimazione nel
tempo, si potrebbe scegliere di implementare direttamente di ordine 4 la
DFT come illustrato in figura 7.18. Si noti che nelle due farfalle risultanti
a radice 4, si sono indicati i coefficienti:
W2 come –j;
W4 come –1 e
W6 come j. (ricordare che N =8).
M. Usai
Circuiti digitali 7_5
14
Ciò enfatizza il fatto che questi coefficienti non richiedono
attualmente moltiplicazioni perché
W2(a+jb)=b-ja;
W4(a+jb)=-a-jb;
W6(a+jb)=-b+ja.
Gli algoritmi FFT a radice 2 e a radice 4 sono i più comuni sebbene
altri valori di radice possono essere impiegati (e sono richiesti se
N≠2r)
M. Usai
Circuiti digitali 7_5
15
7.18 FFT ottenuta con una decimazione nel tempo con 8 punti incorporando 2 farfalle a radice 4
M. Usai
Circuiti digitali 7_5
16
Per esempio per valutare una FFT a 320 punti, si possono usare
farfalle a radice 2 e a radice 5 o farfalle a radice 4 e radice 5 o tutti e
tre.
Così le FFT sono dette essere algoritmi a radice mista (mixed radix).
Sono utilizzabili diversi programmi FFT [16].
Dati a valore reale
Poiché più subroutines FFT o hardware accettano i dati input con
valori complessi, stiamo sprecando alcune delle potenzialità
dell’algoritmo che si hanno quando i dati di input sono valori reali.
Questa potenzialità sprecata può facilmente essere utilizzata.
Se si hanno due sequenze ~x1 (n) e ~x2 (n) da trasformare, supponendo
che le corrispondenti di DFT siano:
~
~
~
X 1 (k ) = E1 (k ) + jO1 (k ),
~
~
~
X 2 (k ) = E2 (k ) + jO2 (k )
M. Usai
Circuiti digitali 7_5
(7.4.12)
17
~
E
dove, come riportato nelle tabelle 7.1, le parti reali i ( k ) sono funzioni
~
O
pari di k e le parti immaginarie i (k ) sono dispari cioè:
~
~
Ei (k ) = Ei ( N − k ),
(7.4.13)
~
~
Oi (k ) = −Oi ( N − k )
Formando la sequenza composta di input a valore complesso:
~
x ( n) = ~
x1 (n) + j ~
x2 (n),
(7.4.14)
~
X
(k ) che per la linearità è semplicemente:
si valuta la sua DFT
~
~
~
X ( k ) = X 1 ( k ) + jX 2 ( k )
~
~
~
~
= E1 ( k ) + O2 (k ) + j E2 (k ) + O1 (k )
[
M. Usai
] [
Circuiti digitali 7_5
]
(7.4.15)
18
Quindi dalla 7.4.13
[
] [
~
~
~
~
~
X ( N − k ) = E1 ( k ) − O2 ( k ) + j E2 ( k ) − O1 ( k )
]
~
~
~
X
(
k
)
X
(
k
)
X
e le DFT desiderate 1
e 2
possono essere ricavate da (k )
attraverso:
~
~
+
X
(
k
)
X
* (N − k)
~
=
X 1 (k )
2
(7.4.16)
~
~
X (k ) − X * ( N − k )
~
X 2 (k ) =
2j
dove * indica il complesso coniugato.
M. Usai
Circuiti digitali 7_5
19
Convoluzione ad alta velocità
L’implementazione di un filtro FIR corrisponde al calcolo della
convoluzione lineare
• della sequenza di dati x(n) e
• della risposta ad impulso di durata finita h(n) di ordine M.
Se inoltre la sequenza di dati ha una durata finita N1 diverso da
M, la convoluzione lineare può essere implementata
moltiplicando le corrispondenti DFT sulle quali si è
precedentemente eseguito lo zero-padding a N2 >> N1+M
campioni, come descritto in figura 7.2.
Il vantaggio potenziale di questo approccio è che l’algoritmo
FFT può essere usato per calcolare la DFT riducendo il
numero delle moltiplicazioni e addizioni.
M. Usai
Circuiti digitali 7_5
20
Figura 7.2 Lo zero padding delle sequenze della figura rende la convoluzione
circolare equivalente alla convoluzione lineare
M. Usai
Circuiti digitali 7_5
21
In particolare,
- il calcolo diretto della convoluzione dovrebbe richiedere circa
M⋅N1 operazioni reali (moltiplicazioni addizioni), mentre
- la FFT dei dati zero-padded comporta circa N2 ⋅ log N2 valutazioni
complesse per N2 >> N1+M, il prodotto delle DFT richiede N2
calcoli complessi e la FFT inversa del prodotto richiede altri
N2log N2 calcoli complessi (si assume che la DFT zero-padded di
h(n) sia sempre utilizzabile e che non debba essere calcolata).
Questo approccio è stato chiamato convoluzione ad alta velocità
(high-speed convolution) [64].
Spesso le sequenze di lunghezza N1 sono troppo grandi per
permettere una valutazione di una singola DFT di dati.
Questo è soprattutto vero nei sistemi a tempo reale, dove la
sequenza dei dati di input è di durata infinita.
M. Usai
Circuiti digitali 7_5
22
In questi casi:
• le sequenze dei dati possono essere divise in sequenze più corte di
conveniente lunghezza, e
• ciascun segmento convoluto con h(n) attraverso le DFT.
Quindi ci saranno effetti finali dovuti a ciascuna convoluzione come
descritto nei paragrafi 7.1 e 7.2, delle quali si deve tener conto
quando i segmenti vengono ricombinati per produrre una sequenza
di output.
Esistono due procedure per effettuare questa segmentazione e
ricombinazione dei dati: overlap_add e overlap_save.
M. Usai
Circuiti digitali 7_5
23
Nel metodo overlap-add,
la sequenza di input viene divisa in segmenti non-sovrapposti xk(n) di
lunghezza N1=N2-M dove N2 è la lunghezza desiderata della FFT e ciascun
segmento zero-padded è convoluto con h(n) per produrre un segmento yk(n) di
lunghezza N2.
x ( n) =
Poiché:
∑ xk ( n)
k
(7.4.17)
e la convoluzione è un’operazione lineare, l’output y(n) è semplicemente:
y ( n) = ∑ y k ( n)
(7.4.18)
Comunque ciascun segmento di output yk(n) si sovrappone al segmento seguente
yk+1(n) negli M campioni e quindi la (7.4.18) implica una addizione reale di
segmenti non semplicemente una concatenazione come nella (7.4.17).
Nei tratti di lunghezza L intermedi le convoluzioni parziali, quando si sommando
tra di loro le sequenze filtrate, danno come risultato una convoluzione esatta.
k
M. Usai
Circuiti digitali 7_5
24
Quindi i segmenti di output vengono “overlapedd” (sovrapposti) e
“added” (“sommati”),. Ciò è illustrato in figura 7.19.
Figura 7 19 Rappresentazione del metodo overlap-add
M. Usai
Circuiti digitali 7_5
25
Nel metodo overlape-save invece vengono overlapped (sovrapposti) i
segmenti di input mentre i segmenti di output vengono troncati per non
essere sovrapposti e quindi concatenati. In particolare i segmenti di
input xk(n) di lunghezza N2 vengono presi con un overlap di M
campioni tra i segmenti.
Le convoluzioni circolari della xk(n) e h(n) attraverso le DFT a N2 punti
producono i segmenti di output yk(n) in cui i primi M campioni non
sono utilizzabili perché sono affetti da equivocazione temporale.
Quindi i primi M campioni di ciascun yk(n) vengono scartati come
illustrato in figura 7.20 e segmenti risultanti a N1 punti vengono
concatenati per produrre y(n).
M. Usai
Circuiti digitali 7_5
26
Figura 7.20 Rappresentazione del metodo overlap-save
In entrambi i metodi la generazione di N1 campioni di output richiede circa N2
log N2 calcoli complessi.
Chiaramente per evitare eccessiva overlap, si sceglierà generalmente:
N1 > M e spesso
N1 >> M.
M. Usai
Circuiti digitali 7_5
27
Stockham[64] ha determinato che per un incremento effettivo della
velocità di calcolo attraverso una convoluzione “high-speed”:
M deve essere almeno uguale a 32.
Sono riportati di seguito i fattori approssimati di incremento della
velocità, calcolati da Stockham, :
Filter Order (M)
16
32
64
128
256
512
1024
Speed-up Factor
0.7
1.3
2.3
4
6
13
24
Per valori grandi di M, anche la risposta impulsiva h(n) può essere
segmentata per produrre le DFTs della lunghezza desiderata.
M. Usai
Circuiti digitali 7_5
28