Induzione elettromagnetica
1. Induzione elettromagnetica
2. Esperienze di Faraday
3. Legge di Faraday – Neumann – Lenz
Induzione elettromagnetica (1)
La rivoluzione determinata dall'utilizzo dell'energia
elettrica su larga scala non poteva fondarsi sulla
produzione di corrente ad opera della pila di Volta.
Ci voleva un modo più efficace di produrre corrente.
Spesso, nella storia della fisica, si è ragionato per
analogie e simmetrie;
nel
caso
dell'elettromagnetismo
gli
scienziati
dell'epoca si domandarono:
Se la corrente genera un campo magnetico, può un
campo magnetico generare una corrente?
Nel 1821, un anno dopo la scoperta di Oersted, il
giovane
inglese
Michael
Faraday
(1791-1867),
assistente di chimica autodidatta, ebbe l'incarico di
compilare una storia delle esperienze recenti
sull'elettromagnetismo.
Michael Faraday (1791-1867)
Induzione elettromagnetica (2)
Faraday ripeté le esperienze nel suo laboratorio e ne
programmò altri;
si soffermò in particolare sull'andamento della forza
magnetica nello spazio che descrisse in termini di
linee di campo.
Fu Faraday, come già sappiamo, il primo a proporre la
descrizione grafica del campo magnetico (e in seguito
anche quella del campo elettrico) in termini di linee di
campo, cui attribuiva una vera e propria presenza
fisica
nello
spazio,
mentre
gli
scienziati
contemporanei ne parlavano in termini di azione a
distanza.
Nel 1824 Faraday tentò di produrre corrente per
mezzo del magnetismo e a questo problema dedicò
diversi anni, finché, nel 1831, arrivò quasi per caso
alla soluzione del problema.
Michael Faraday (1791-1867)
Induzione elettromagnetica (3)
Nel 1831 Faraday (1791-1867) scoprì il
fenomeno dell’ induzione magnetica, la
creazione cioè di un campo elettrico per mezzo
di un campo magnetico.
Essa è di fondamentale importanza in quanto, a
differenza dell’elettromagnetismo che fornisce
i mezzi per trasformare l’energia elettrica in
lavoro (vedi motore elettrico)
l’induzione elettromagnetica fornisce i mezzi
per trasformare il lavoro meccanico in corrente
elettrica.
Le centrali elettriche si basano sul principio
dell’induzione.
Michael Faraday (1791-1867)
Induzione elettromagnetica (4)
Una carica elettrica in quiete
genera
nello spazio circostante
un campo elettrico
Induzione elettromagnetica (5)
Un magnete in quiete
genera
nello spazio circostante
un campo magnetico
Induzione elettromagnetica (6)
Una corrente elettrica
(cariche elettriche in
movimento di moto uniforme)
genera
nello spazio circostante un
campo magnetico
con le stesse proprietà di
quello creato da un magnete.
X
Induzione elettromagnetica (7)
Un campo elettrico
genera
un campo magnetico
Viceversa:
Un campo magnetico riesce a generare
una corrente elettrica?
(e quindi una ddp ed un campo elettrico)
Induzione elettromagnetica (8)
Dai suoi esperimenti Faraday scopre che
1. Un campo magnetico
variabile genera
una f.e.m. indotta (cioè si
assiste alla circolazione di corrente anche in
circuiti senza generatore)
2. Il campo magnetico
indotto è tale da opporsi
alla causa che l’ha
generato (cioè la corrente indotta crea a
sua volta un campo magnetico che si va ad
opporre a quello esistente)
Esperienze di Faraday (0)
Magnete fermo, circuito fermo:
quando non c’è moto relativo fra il
magnete ed il circuito
non si induce
un campo elettrico
Esperienze di Faraday (1)
1.Magnete in moto – circuito fermo
Se c’è moto relativo magnete - circuito,
si produce un campo elettrico.
La d.d.p. che si produce si dice
f.e.m. indotta
e la corrente che circola si dice corrente indotta
Esperienze di Faraday (1)
Infatti se un magnete è posto vicino ad un circuito conduttore chiuso, nel
circuito si manifesta una f.e.m. quando il magnete è messo in movimento.
Tale f.e.m. è rilevabile sotto forma di corrente, cioè delle cariche libere
messe in moto nel conduttore, mediante un amperometro.
Si verifica che l’entità della f.e.m., e quindi della corrente, dipende dalla
velocità del moto del magnete relativamente al circuito.
La corrente ha direzione nel circuito che dipende dal fatto che
il magnete sia avvicinato o allontanato.
Esperienze di Faraday (2)
2. Magnete fermo – circuito in moto
Se c’è moto relativo tra magnete - circuito,
si produce un campo elettrico
e quindi
una f.e.m. indotta.
Esperienze di Faraday (3)
3. I circuito fermo – II circuito in moto
Se c’è moto relativo circuito - circuito,
il circuito induttore produce
nel circuito indotto (senza generatore)
una f.e.m. indotta
circuito indotto
circuito induttore
Esperienze di Faraday (3)
Infatti un fenomeno analogo al “circuito fermo – magnete in movimento” si
manifesta se al posto del magnete in movimento abbiamo un circuito in cui
la corrente varia col tempo: “circuito fermo – circuito in movimento”.
Si verifica che se il circuito con corrente variabile genera un campo
magnetico, concatenato al circuito in cui misuriamo la corrente, osserviamo
una f.e.m. indotta, e quindi una corrente indotta.
Esperienze di Faraday (4)
Posso produrre una f.e.m. indotta:
1.variando l’intensità della corrente
elettrica nel circuito induttore
Esperienze di Faraday (5)
Posso produrre una f.e.m. indotta:
2.variando la superficie del circuito immerso
nel campo magnetico
Esperienze di Faraday (6)
Posso produrre una f.e.m. indotta:
3.variando l’angolo di rotazione della bobina
immersa nel campo magnetico
(Spira rotante in un c. magnetico stazionario)
Esperienze di Faraday (7)
Posso produrre una f.e.m. indotta:
4.Conduttore in movimento in un campo magnetico stazionario.
Gli elettroni di
conduzione nella
sbarretta PQ “sentono”
una forza che li mette in
moto verso Q.
Se le cariche si muovono,
significa che nella
barretta si viene a creare
un campo elettrico.
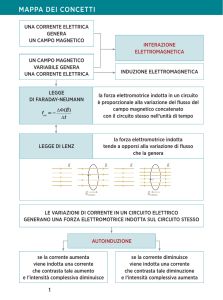
Induzione elettromagnetica
La f.e.m. legata al movimento è un aspetto particolare di un
fenomeno più generale detto induzione elettromagnetica.
Viene indotta nel circuito una f.e.m. indotta finché dura nel
tempo una variazione:
1. Dell’intensità, del verso, della direzione o di una qualunque
combinazione di essi di un campo magnetico intercettato da un
circuito oppure
2. Dell’area di un circuito immesso in un campo magnetico oppure
3. Dell’ orientamento del circuito nel campo magnetico
f.e.m. indotta in un conduttore in moto
Consideriamo la sbarretta metallica di lunghezza l che si muove verso destra, con
velocità v costante e perpendicolare al campo magnetico uniforme B.
Ogni carica q dentro la sbarretta si muove con la stessa velocità v e risente di una
forza di Lorentz FL = qvB.
Con la regola mano destra, valutiamo lo spostamento degli elettroni di conduzione che
sono spinti verso Q e lasciano in P la stessa quantità di carica positiva.
Se la sbarretta è isolata, le cariche + e – si accumulano fino a quando la repulsione
elettrostatica tra esse diventa uguale alla forza magnetica.
Quando le due forze si bilanciano, si raggiunge l’equilibrio e non avviene più alcuna
separazione di carica.
P
FL = q v × B
FL
Q
f.e.m. indotta in un conduttore in moto
Ma se la sbarretta conduttrice si muove, perpendicolarmente ad un campo magnetico
uniforme, a contatto con una guida conduttrice che forma un circuito, le cariche
accumulatesi agli estremi della sbarretta possono scorrere lungo la guida e la f.e.m.
indotta dalla forza di Lorentz genera una corrente indotta i nel circuito.
FL
conseguenza della forza di Lorentz
f.e.m. indotta in un conduttore in moto
Le cariche separate all’estremità del conduttore in movimento
danno luogo ad una f.e.m. indotta dovuta al movimento della
sbarretta.
La f.e.m. esiste finché la sbarretta si muove.
FL = q v × B
Se la sbarretta si ferma, la forza di Lorentz si annulla, con il
risultato che l’attrazione elettrostatica riunisce le cariche + e – e
la f.e.m. si annulla.
La f.e.m. della sbarretta è simile a quella tra i poli di una batteria.
La f.e.m. della batteria è ottenuta da reazioni chimiche, mentre la
f.e.m. in questo caso è generata dall’agente esterno che sposta la
sbarretta nel campo magnetico (p.es. la mano).
f.e.m. indotta in un conduttore in moto
Determinazione dell’intensità della f.e.m. dovuta al movimento:
Il lavoro sugli elettroni di conduzione non è compiuto da un generatore, ma
dalla forza di Lorentz , che li sposta lungo la sbarretta di lunghezza l.
Il lavoro compiuto da FL è :
LL = FL ⋅ l = e v B l
La f.e.m. indotta si ottiene dal rapporto tra il lavoro compiuto per spostare
una carica e la carica stessa.
LL e v B l
f .e.m. =
=
=vBl
e
e
Se la resistenza del circuito è R,
in esso scorrerà una corrente
vBl
i=
R
f.e.m. indotta in un conduttore in moto
A questo punto qualcuno si starà chiedendo …….
Ma non ci aveva detto che la Forza di Lorentz non compie lavoro?
A cosa è dovuta questa evidente contraddizione?
Teniamo presente che gli elettroni che si stanno muovendo nella sbarretta in
movimento NON SONO COMPLETAMENTE LIBERI DI MUOVERSI (come
accadeva agli elettroni lanciati con velocità v in un campo magnetico
uniforme), ma sono vincolati a farlo nella direzione parallela alla sbarretta
conduttrice.
La velocità degli elettroni lungo la sbarretta non è solo v , ma v + v d
cioè è data dalla velocità di trascinamento sommata alla velocità di deriva
f.e.m. indotta in un conduttore in moto
La forza magnetica complessiva che agisce sui singoli elettroni è:
F = −e(v + v d )xB = −ev xB − ev d xB
Fd
Fv
Ftot = Fv + Fd
f.e.m. indotta in un conduttore in moto
L’energia elettrica che si ottiene per mezzo del fenomeno dell’induzione
magnetica non viene dal nulla !!!
Ciò che si ritrova sotto forma di corrente elettrica non è altro che il lavoro
meccanico compiuto per muovere la sbarra (o per far ruotare la spira: devo
contrastare il momento della forza).
Infatti si deve contrastare la forza F che si viene ad esercitare sulla
sbarretta in quanto a) è percorsa da corrente b) è immersa nel campo
magnetico. Tale forza ha modulo pari a
della velocità. Pag(247)
F
Bil e ha verso opposto a quella
Dimostrazione della legge di Faraday Neumann
Determiniamo matematicamente la legge di Faraday- Neumann servendoci di un
caso particolare, anche se la legge ha validità del tutto generale, nel senso che
ogni volta che il flusso Φ (B) del campo magnetico, attraverso la superficie
delimitata dal circuito, varia nel tempo, si genera una f.e.m indotta e perciò una
corrente indotta nel circuito tali che f.e.m = Ri.
La produzione della corrente indotta
dipende dalla rapidità con cui varia il
flusso di B nel tempo, infatti la
corrente è più intensa quanto più è
rapida la variazione di Φ (B).
da pag. 247 Caforio
Descrizione della situazione
Consideriamo il caso di un campo magnetico uniforme, perpendicolare al foglio,
come in figura, e di una spira che viene estratta dal campo con velocità v.
La spira è parallela al foglio.
Estraendo la spira dal campo magnetico si produce in essa una f.e.m indotta, e
quindi una corrente indotta, che cessa se fermiamo la spira. Questo accade
perché gli elettroni di conduzione si muovono anch’essi con velocità v mentre
muoviamo la spira e risultano soggetti alla forza di Lorentz
FL = qv ∧ B = −ev ∧ B
avendo indicato con e la carica elementare dell’elettrone
e con il segno meno la sua carica.
Dimostrazione della legge di Faraday Neumann
Con la regola della mano destra si verifica che la forza F è
diretta da A verso B.
Lungo il tratto AB della spira gli elettroni si muovono da A verso
B per effetto della forza di Lorentz.
Nella spira si genera una corrente indotta diretta da B verso A.
Lungo i lati AD e BC la forza di Lorentz è diretta
perpendicolarmente e non provoca il moto degli elettroni di
conduzione lungo tali lati.
Il lato DC è fuori dal campo magnetico e i suoi elettroni non
subiscono alcuna forza.
Gli unici responsabili della corrente indotta
sono, pertanto, gli elettroni del lato AB.
Dimostrazione della legge di Faraday Neumann
La situazione può anche essere interpretata come segue:
possiamo pensare che il lato AB si comporti come una pila, visto
che è il responsabile della corrente circolante nella spira;
per ottenere lo stesso effetto potremmo inserire
al posto del lato AB una pila nella spira ferma, avente il polo - in
B e il polo + in A che generi una d.d.p. uguale a quella che fa
circolare corrente nella spira.
Calcolo della forza elettromotrice
Ricordando la legge che esprime la d.d.p. tra due punti a distanza
d: ∆V = E ⋅ d possiamo pensare di applicarla al lato AB della spira.
Chiamando l la sua lunghezza e
∆V = E ⋅ l
⇒
E=
∆V
∆V = f .e.m.
⇒
l
abbiamo :
f .e.m.
E=
l
Possiamo quindi ritenere che la d.d.p. che si crea tra A e B sia la
causa del moto degli elettroni, come se ad essi fosse applicata la
forza elettrica :
f .e.m.
F = q ⋅ E = − e ⋅ E = −e
Questa forza è in modulo uguale alla forza ldi Lorentz: pertanto
si ha
f .e.m.
F = −e ⋅
= −e ⋅v ⋅B ⇒
l
f .e.m.
= v ⋅ B ⇒ f .e.m. = v ⋅ B ⋅ l
l
.
Calcolo della variazione del flusso del C.M.
Passiamo ora al calcolo del flusso del campo magnetico attraverso la superficie
delimitata dalla spira che sta uscendo dal campo magnetico con velocità .
Sia ∆x il tratto in uscita percorso dalla spira nel tempo ∆t, con ∆x = v ∆t. Nel
tempo ∆t il flusso del campo magnetico subisce questa variazione:
[ ] = −Bl∆x
∆Φ = Φ finale − Φ iniziale = [Bl (l − ∆x )] − Bl
2
in quanto il flusso si ottiene dal prodotto scalare del campo magnetico B
per la superficie attraversata ( essendo qui la spira perpendicolare a B )
Vedi figura pag. 251
.
Legge di Faraday-Neumann
Tenete presente che la variazione di flusso è negativa perché la spira sta
uscendo dal campo e diminuisce la porzione di superficie attraversata
dalle linee di forza di B.
Calcoliamo ora il rapporto tra ∆Φ e ∆t, cioè la variazione del flusso nel
tempo e osserviamo facilmente che esso è l’opposto della fem f già
trovata prima.
∆Φ
∆x
= −B ⋅ l ⋅
= −Blv = f .e.m.
∆t
∆t
Scriviamo pertanto la legge di Faraday e deduciamo anche il valore della
corrente indotta
∆Φ
f .e.m. = −
∆t
⇒
1 ∆Φ
i=−
R ∆t
Legge di Faraday (1)
Sperimentalmente si osserva che:
Se una carica elettrica o un circuito chiuso privo di generatori di f.e.m.
si trovano immersi in un campo magnetico variabile nel tempo, la carica si mette
in movimento mentre il circuito risulta percorso da una corrente indotta e
quindi si genera una f.e.m. indotta.
∆Φ
f.e.m. = −
∆t
che è la f.e.m indotta che si genera, IN
MEDIA, nel circuito durante l’intervallo
di tempo considerato.
Flusso dell’induzione magnetica
concatenato con la linea chiusa
Legge di Faraday (2)
Legge di Faraday-Neumann
In un circuito immerso in un campo magnetico si produce una f.e.m. pari
alla rapidità di variazione del flusso del campo magnetico nel tempo,
cioè, calcolando il limite per ∆t che tende a zero, pari alla derivata
rispetto al tempo del flusso del campo magnetico attraverso il circuito
stesso:
dΦ (B)
f.e.m.indotta = −
dt
Legge di Lenz
Legge di Lenz (1)
Il segno – che compare nella formula prende il nome di
Legge di Lenz
La corrente indotta in una spira conduttrice chiusa ha un verso tale da opporsi alla
variazione che l’ha generata.
Il segno della f.e.m. indotta è tale da creare una corrente che a sua volta genera un
campo magnetico che si oppone alla variazione del campo magnetico che ha indotto la
f.e.m. , in piena coerenza con il PRINCIPIO DI CONSERVAZIONE DELL’ENERGIA
La corrente indotta ha sempre verso tale
da opporsi alla causa che l’ha generata
Legge di Lenz (2)
dΦ ( B )
fem i = −
dt
1 dΦ ( B )
ii = −
R dt
Legge di Faraday-Neumann-Lenz (2)
Il risultato ottenuto è valido anche se L non è un conduttore, ma è una curva
chiusa ideale.
In conclusione possiamo affermare che:
un campo magnetico dipendente dal tempo genera un campo elettrico indotto tale che
la circuitazione del campo elettrico lungo un percorso arbitrario chiuso sia eguale ed
opposta alla derivata rispetto al tempo del flusso del campo magnetico attraverso una
superficie avente per contorno quel percorso.
dΦ ( B )
f.e.m.indotta = −
dt
III equazione di Maxwell
Legge di Faraday-Neumann-Lenz (3)
Conclusione:
la legge dell’induzione elettromagnetica, può essere impiegata quando la
variazione del flusso magnetico è dovuta:
ad una variazione del campo magnetico o
ad un movimento o
ad una deformazione rispetto al campo magnetico del circuito lungo il
quale è calcolata la f.e.m., o
ad una azione combinata di questi processi.
Su questa legge si basa il funzionamento del generatore elettrico e del
trasformatore.
f.e.m.indotta
dΦ ( B )
=−
dt
Alternatore
L’esperimento di
Faraday è, in pratica,
l’invenzione
dell’alternatore, in cui
la variazione di flusso
di B è ottenuta facendo
ruotare una serie di
bobine all’interno di un
campo magnetico
Alternatore
E’ da notare che
l’alternatore non
produce energia dal
nulla, ma converte in
elettrica l’energia
meccanica sviluppata
generalmente da moto
di una turbina, a sua
volta azionata o
dall’acqua o dal vapore
Dinamo
Nella dinamo la
bobina è invece
fissa, mentre sono
dei magneti
permanenti a
ruotare
Trasformatore
Nel trasformatore una
corrente alternata in
una bobina (inducente)
produce una variazione
di flusso magnetico in
una seconda bobina
(indotta) e quindi una
ddp, ovvero una
corrente indotta, con
intensità e tensione
diverse dalla corrente
originaria