Proprietà meccaniche dei
ceramici
Modulo elastico
La presenza di legami ionici e covalenti conferisce valori di E generalmente
maggiori di quelli riscontrati nei materiali metallici. Ancora più elevato risulta il
modulo specifico E/ρ per la bassa densità dei ceramici.
Materiale
E (GPa)
ρ (g/cm-3)
E/ρ (GPa/gcm-3)
Acciaio
210
7.8
27
Lega di Al
70
2.7
26
Allumina, Al2O3
390
3.9
100
Silice, SiO2
69
2.6
27
Cemento
45
2.4
19
Modulo specifico di metalli e ceramici
Modulo elastico
Il modulo elastico si misura come nel caso dei metalli
Durezza
I materiali ceramici sono i più duri di cui si disponga. Nel confronto con leghe
metalliche anche la loro durezza normalizzata H/E risulta comunque superiore.
I materiali metallici sono intrinsecamente teneri, mentre i ceramici sono
intrinsecamente duri.
Metalli H/E
Leghe metalliche
H/E
Ceramici
H/E
Diamante
1.5x10-1
Cu
1.2x10-3
Ottone
9x10-3
Al
1.5x10-3
Dural (Al4%Cu)
1.5x10-3 Allumina
4x10-2
Ni
9x10-4
Acciaio Inox
6x10-3
6x10-2
Fe
9x10-4
Acciaio
1.5x10-3 SiC
Zirconia
6x10-2
Valori normalizzati di durezza di metalli puri, leghe e ceramici
Scorrimento dislocazioni
Il reticolo dei ceramici si oppone al movimento delle dislocazioni. La resistenza al
movimento delle dislocazioni si ha su tutti i piani e lungo tutte le direzioni
reticolari. Nel caso dei legami covalenti il movimento delle dislocazioni comporta la
rottura e la riformazione di legami molto forti nella zona in cui sono concentrati gli
elettroni che formano il legame.
Nel caso di legami ionici la presenza di ioni negativi e positivi impedisce il
movimento perché si troverebbero vicini ioni della stesso segno.
Movimento dislocazioni in metalli, ceramici covalenti e ionici
Prove meccaniche
Misura della resistenza meccanica. Si possono eseguire tre diverse prove che
forniscono risultati diversi tra loro.
Prove per misurare la resistenza a frattura nei materiali ceramici: a) prova di
trazione, b) prova di flessione, c) prova di compressione.
Misura della resistenza meccanica
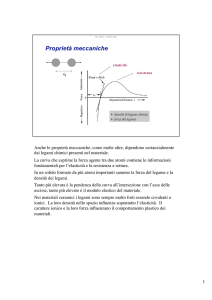
La curva σ-ε dei ceramici non si valuta attraverso la prova di trazione perche:
•è difficile preparare i provini di una specifica geometria
•è difficile serrarli alle morse di trazione
•i provini si rompono allo 0.1% di allungamento (bisognerebbe garantire la perfetta
assialità per evitare componenti di flessione).
La prova di flessione misura la forza necessaria a portare a rottura una barretta per
flessione e si indica con il modulo di rottura: σR
La normativa prevede lo svolgimento di prove di flessione a 3 o 4 punte su provini
rettangolari o circolari.
Prova di flessione
Nel punto di carico la superficie superiore del provino è soggetta a compressione,
mentre quella inferiore a trazione.
I materiali ceramici risultano più resistenti in flessione che in trazione perché in flessione
una parte del provino è sollecitato in compressione e il difetti di dimensioni maggiori può
trovarsi distante dalla superficie inferiore sollecitato in trazione.
Lo sforzo viene calcolato conoscendo lo spessore del provino, il momento flettente
e quello di inerzia:
σ Rrett
3FL
=
2bd 2
σ Rcirc =
FL
ρR 3
Resistenza a flessione
Prova di compressione
Mentre nel caso dei materiali metallici i valori di resistenza meccanica ottenuti da una
prova di trazione sono circa uguali a quelli ottenuti con una prova di compressione, nel
caso dei materiali ceramici:
σ C ≈ 15σ T
Trazione
La spiegazione di questo diverso comportamento è
legata alla presenza delle microcricche che, sotto
sforzo di compressione, si propagano in modo
stabile disponendosi in modo parallelo alla
direzione di applicazione del carico.
La rottura non è causata dalla propagazione rapida
di una cricca, come nel caso della trazione, ma
dalla lenta propagazione di più cricche fino a
determinare lo sgretolamento di una zona.
Compressione
Resistenza meccanica
La resistenza a trazione dei ceramici dipende alla dimensione del provino. In generale,
minore è il volume del provino a minore è la probabilità di trovare un difetto di dimensioni
maggiori.
La resistenza media di campioni di ceramico di piccole dimensioni è maggiore di quella di
un campione di grandi dimensioni.
Probabilità di rottura
La resistenza dei ceramici in termini statistici. Quando si utilizzano materiali fragili non è
possibile escludere la rottura di un componente sotto determinate condizioni di carico.
Esiste sempre una probabilità di rottura Pf
La progettazione di componenti con materiali fragili richiedere che la probabilità di rottura
sia compatibile con un accettabile livello di rischio derivante dalla rottura del componente.
La probabilità di rottura è legata alla distribuzione della dimensione dei difetti
(microcricche e pori angolari) ed alla probabilità di trovare difetti di determinate
dimensioni.
In presenza di difetti non si può definire un valore preciso del carico di rottura, si deve
piuttosto parlare della probabilità che un determinato campione abbia un dato carico di
rottura o una data resistenza.
La distribuzione della dimensione dei difetti comporta che campioni più grandi si rompano
mediamente sotto carichi minori in quanto esiste una probabilità che contengano difetti
più grandi.
Ciò spiega anche perché il modulo di rottura sia maggiore del carico di rottura.
Probabilità di rottura
Probabilità di sopravvivenza:
PS (V0 ) = e
σ
−
σ0
m
Rappresenta la frazione di campioni identici di volume V0 che si rompono sotto il carico a
trazione σ; m e σ sono costanti.
•Per σ =0 PS = 1 tutti i campioni restano integri
•Per σ → ∞ PS → 0
1
• Per σ=σ0 PS = = 0.37 dunque σ0 rappresenta il valore dello sforzo che permette la
e
sopravvivenza del 37% dei campioni.
•al crescere di σ diminuisce il numero di campioni che sopravvivono
•m rappresenta la rapidità con cui PS diminuisce quando σ → σ o
La costante m è il Modulo di Weibull
Più è piccolo è m, maggiore è la variabilità della resistenza, maggiore è m più uniforme è il
comportamento.
Probabilità di rottura
CERAMICI TRADIZIONALI
CERAMICI STRUTTURALI
METALLI
m~5
m~10
m~100
I valori di m e σ0 si determinano sperimentalmente determinando la frazione di campioni
che sopravvivono a carichi diversi σ1, σ2, σ3…..e riportando i risultati nel diagramma.
Diagramma di probabilità di Weibull
1 σ
=
ln
Ps (Vo ) σ 0
m
1
σ
= m ln
ln ln
σ0
Ps (Vo )
La pendenza della retta è m. σ0 è il valore di σ per il quale PS (V0 ) = 0.37
Probabilità di Weibull
Probabilità di Weibull
Prodotti ceramici
Prodotti ceramici
Fabbricazione e trattamenti
Fabbricazione e trattamenti
Fabbricazione e trattamenti
Fabbricazione e trattamenti
Fabbricazione e trattamenti
Fabbricazione e trattamenti