E
Esercizi
sul momento meccanico
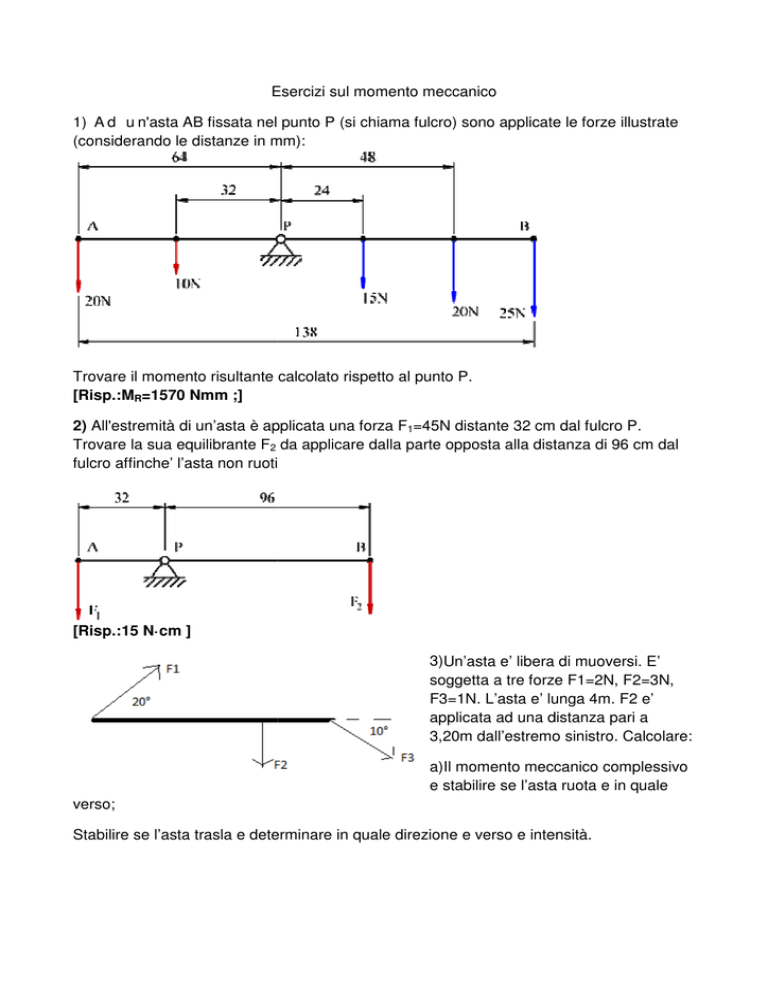
1) A d u n'asta AB fissata nell punto P (si chiama fulcro) sono applicate
te le forze illustrate
(considerando le distanze in mm):
m
Trovare il momento risultante calcolato rispetto al punto P.
[Risp.:MR=1570 Nmm ;]
2) All'estremità di un’asta è ap
pplicata una forza F1=45N distante 32 cm dal fulcro P.
Trovare la sua equilibrante F2 da applicare dalla parte opposta alla dist
stanza di 96 cm dal
fulcro affinche’ l’asta non ruoti
ti
[Risp.:15 N·cm ]
3)Un’asta e’ libera
a di muoversi. E’
soggetta a tre forze
ze F1=2N, F2=3N,
F3=1N. L’asta e’ lu
lunga 4m. F2 e’
applicata ad una distanza
d
pari a
3,20m dall’estremo
o sinistro. Calcolare:
a)Il momento mecc
ccanico complessivo
e stabilire se l’asta
ta ruota e in quale
verso;
Stabilire se l’asta trasla e dete
terminare in quale direzione e verso e inten
ensità.
Svolgimento:
Se l’asta e’ libera di muoversi e puo’ ruotare , tutti i suoi punti ruotano . Possiamo scegliere
un punto qualunque per calcolare i momenti delle singole forze.
Se scelgo il centro dell’asta come punto di riferimento per calcolare i momenti si ha:
La forza F1ha una distanza pari a 2m dal centro dell’asta (assunto come centro di
rotazione). Il momento meccanico sara’:
τ = − F1⋅ sen20 ⋅ 2 = 2 ⋅ sen20 ⋅ 2 = −1,4 N ⋅ m
La forza F1 fa ruotare il corpo intorno al centro in senso orario e quindi il momento e’
negativo.
La forza F2 dista 1,20m dal centro e fa ruotare l’asta in senso antiorario e quindi il
momento meccanico e’ negativo.
τ = F 2 ⋅ 1,20 = 3 ⋅ 1,20 = 3,6 N ⋅ m
La forza F3 fa ruotare l’asta in senso orario e quindi il momento e’ negativo. La forza dista
dal centro 2m.
τ = F 3 ⋅ sen10 ⋅ 2 = 3 ⋅ sen10 ⋅ 2 = −1N ⋅ m
IL momento totale sara’:
τ = −1,4 + 3,6 − 1 = 1,2 N ⋅ m
Il risultato e’ positivo e quindi l’asta ruota in senso antiorario.
L’asta e’ libera di muoversi e quindi puo’ anche traslare. Se trasla in quale direzione
trasla?
Scomponiamo le forze nelle componenti orizzontali e verticali e calcoliamo le risultant Sx e
Sy come abbiamo gia’ fatto:
Sx=-F1cos20+F3cos10=2cos20+1cos10=2,9N(la forza F2 e’ verticale quindi F2x=0)
Sy=F1sen20-F2-F3sen10=-2,5N
2
2
La risultante e’ S = Sx + Sy = 3,8 N
La direzione lungo la quale si muove e’
α = cos −1 (
Sx
2,9
) = cos −1 ( ) = 40°
S
3,8
L’asta allora ruota e trasla contemporaneamente. Il suo moto e’ di rototraslazione.
4)Risolvete un analogo problema. I dati sono in figura:
L’asta AC e’ lunga 5m La forza F2 e’ applicata
nel punto medio di BC e F4 e’ applicata nel
punto medio di AB. Trova il momento
meccanico complessivo e stabilisci se l’asta e in
quale verso. Determina poi se trasla e
determina in quale direzione e intensità. Segui
lo svolgimento del problema precedente.
5)Un problema inverso.
Segui lo svolgimento del seguente problema:
Un’asta ha una lunghezza di 6m ed e’ soggetta a forze come in figura:
In quale punto B si deve applicare la
forza E (equilibrante) perché l’asta sia in
equilibrio?
L’asta e’ in equilibrio se il momento meccanico totale e’ zero e la somma delle forze e’
zero. Infatti se il momento meccanico e’ zero allora l’asta non ruota e se la somma delle
forze che agiscono e’ zero l’asta non trasla.
Applichiamo la forza equilibrante in un punto B a distanza x dal punto A (scelta arbitraria).
La direzione e’ verticale perché tutte le forze lo sono (ci limiteremo solo a questo caso). Il
verso non possiamo saperlo e quindi lo fissiamo arbitrariamente verso l’alto. Sarà il
risultato a confermare questa scelta. Se il risultato sarà positivo allora l’equilibrante e’
realmente verso l’alto altrimenti la invertiremo.
Non conosciamo ne’ il valore di E ne’ dove e’ applicata. Indichiamo con x la distanza AB.
Vogliamo trovare x.
Perché non ruoti il momento meccanico deve essere zero. Calcoliamolo rispetto ad un
punto qualunque dell’asta. Ad esempio rispetto al punto B.
Il momento di F1 rispetto al punto B e’ τ=F1·x (positivo). Il momento di F2 rispetto a B e’
τ=-F2·(6-x).(negativo).
Il momento di E rispetto al punto B e’ zero perche la distanza da B e’ zero essendo
applicata in B. Pertanto affiche’ il momento complessivo sia zero deve essere:
F1·x-F2·(6-x)=0 cioè 2x-3(6-x)=0 da cui x=18/5m cioè a 3,6 m dal punto A.
Quale intensità deve avere R?
Perché l’asta non ruoti la somma delle forze deve essere zero e quindi:
R-F1-F2=0 da cui R=F1+F2=2+3=5N.
Risultato: per equilibrare l’asta devo applicare una forza di 5N a 3,6m dal punto A e
diretta verso l’alto. (la scelta fatta all’inizio e’ corretta).
6)Risolvi il problema seguente:
L’asta in figura misura 4m. F1=10N e F2= 12N.
Calcola a quale distanza devo applicare
l’equilibrante R perché l’asta non ruoti e non trasli.
(R: X=2,2m dal punto A e R=22N.)
7) Supponiamo che su un’asta lunga 4 m
agiscano piu’ forze e si vuole conoscere quale
forza applicare e in quale punto dell’asta affinche’
resti ferma (in equilibrio). In figura viene mostrata
l’asta divisa in quattro parti uguali e le forze che
su essa agiscono. F1=2N, F2=1,5N, F3=3N,
F4=0,5N, F5=1N.
Perche’ l’asta sia in equilibrio e’ necessario che il momento totale sia zero e la risultante E
delle forze sia zero.
Non sappiamo dove applicare la forza equilibrante E. Pertanto supponiamo che sia
applicata in un punto P distante x dall’estremo A. Non sappiamo in quale verso agisce
pertanto la supporremo diretta verso l’alto (vedi figura). Saranno i risultati a confermare
questa ipotesi oppure a confutarla.
Per calcolare il momento totale scegliamo un qualunque punto dell’asta per esempio il
punto P e calcoliamo il momento di ciascuna forza rispetto a tale punto.
La forza F1 ha un momento τ=-F1·x (negativo);
La forza F2 ha un momento τ =F2·(x-1);(positivo)
La forza F3 ha momento τ =F3·(2-x); (positivo)
La forza F4 ha momento τ =-F4·(3-x)(negativo);
La forza F5 ha momento τ =F5·(4-x) (positivo).
Il momento totale deve essere zero e quindi:
-F1·x+ F2·(x-1)+F3(2-x)-F4·(3-x)+F5·(4-x)=0
Cioè: -2·x+1,5·(x-1)-3·(2-x)-0,5·(3-x)+1·(4-x)=0
Risolvendo l’equazione si trova x=2,5m dal punto A.
Che valore deve avere la risultante? (nella pratica per tenere ferma l’asta la si inchioda
oppure si usa un gancio. Quale forza deve sopportare il gancio? (E’ quello che vogliamo
sapere). La somma delle forze deve essere zero. Essendo tutte forze verticali si possono
sommare. Basta tenere conto del loro segno:
quindi si ha:
F1-F2+E+F3-F4+F5=0 l’incognita e’ E. Risolvendo l’equazione si ha:
E=-F1+F2-F3+F4-F5;
E=-2+1,5-3+0,5-1=-4N
Il risultato negativo vuol dire che E e’ in realtà diretta verso il basso..
8) Risolvi un problema analogo. I dati sono in
figura:
L’asta e’ divisa in 5 parti uguali ed e’ lunga 5m.
F1=2N; F2=2,5N; F3=1N; F4=3N.
Determinare in quale punto si deve applicare una
Equilibrante E perche’ l’asta sia in equilibrio.
(R: E=2,5N verso l’alto e a distanza da A pari a
x=3,8m)
9)L’asta illustrata è sollecitata
a da una massa m=72kg che agisce ad un
na distanza b=12cm
rispetto al fulcro O; consideran
ando la lunghezza L=96cm dell’ asta, trova
vare l'equilibrante F
da applicare alla seconda estr
tremità perché vi sia equilibrio. Inoltre dete
terminare quale forza
R esercita il fulcro.
[ Risp.:F=100,9N ; R=807,2 N ]










