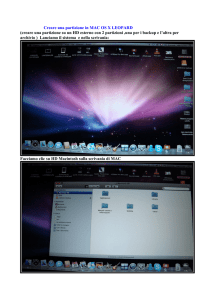
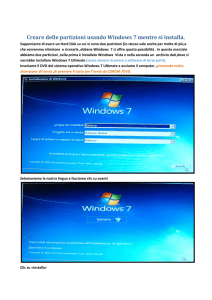
Claudia Montemurro
“SULLE PARTIZIONI DI UN INSIEME”
Ricordiamo la
Definizione: Una partizione di un insieme è una famiglia {X i / i ∈ I } di
sottoinsiemi non vuoti di X tali che:
-
X è l’unione degli insiemi X i ( i ∈ I ), cioè X = U X i
i
-
ogni coppia di sottoinsiemi diversi di X è disgiunta, cioè
X i I X j =∅ per i ≠ j .
I sottoinsiemi X i sono chiamati parti della partizione.
Se X è un insieme finito, una partizione di X deve avere un numero
finito k di parti; perciò utilizziamo IN k = {1,2,..., k } come insieme degli
indici ed elenchiamo le parti come X 1 , X 2 ,..., X k .
I numeri di Stirling
Definizione: Si chiama numero di Stirling di secondo tipo S (n, k ) il
numero delle partizioni di un insieme di ordine n in k insiemi.
ESEMPIO
Sia I = {x, y, z} un insieme di ordine 3 . Si ha:
S (3,1) = 1
l’unica partizione è {I }
S (3,2) = 3
le partizioni possibili sono {{x}, {y, z}}, {{y}, {x, z}}, {{z}, {x, y}}
S (3,3) = 1
l’unica partizione è {{x}, {y}, {z}}
Dal teorema che segue ricaviamo la relazione ricorsiva tra questi numeri.
1
TEOREMA
Sia S (n, k ) il numero di partizioni di un insieme X di n elementi in k
parti, con 1 ≤ k ≤ n . Allora:
S (n,1) = 1
S (n, n) = 1
S (n, k ) = S (n − 1, k − 1) + kS (n − 1, k ) con 2 ≤ k ≤ n − 1 .
Dimostrazione:
Provo banalmente le prime due asserzioni osservando che c’è un’unica
partizione di X con una parte, X stesso, ed un’unica partizione di X in
n parti, formata dai sottoinsiemi unitari {x}, ∀x ∈ X .
Detto z un elemento di X , sia X 0 = X \ {z}. Allora una partizione di X in
k parti si ottiene in uno, e uno soltanto dei seguenti modi:
-
aggiungendo la parte formata dall’insieme unitario z ad una
partizione in k − 1 blocchi di X 0
- aggiungendo l’elemento z ad una delle k parti della partizione di
X 0 e questo si può fare in k modi diversi
Come conseguenza di questo teorema rappresentiamo i numeri di Stirling
mediante una tabella infinita detta triangolo di Stirling, avente come riga
n -esima:
S (n,1), S (n,2),..., S (n, n − 1) S (n, n) .
Indichiamo le prime sette righe del triangolo di Stirling:
2
Osserviamo che, come nel triangolo di Pascal si ha una relazione con i
coefficienti binomiali, così i numeri di Stirling hanno un legame con i
coefficienti multinomiali. Questi contano il numero di permutazioni con
ripetizione di k oggetti in cui il primo è preso n1 volte, il secondo n2
volte, il k -esimo nk volte, con n = n1 + n2 + ... + nk e valgono:
n
n!
=
.
n1n2 ...nk n1!n2 !...nk !
Si osserva che i coefficienti multinomiali sono una generalizzazione dei
coefficienti binomiali e coincidono nel caso in cui k = 2 ; infatti questi
n n n
n!
= = =
, con n = n1 + n2
n1n2 n1 n2 n1!n2 !
ultimi valgono
I numeri di Stirling S (n, k ) ci permettono inoltre di contare le suriezioni
tra due insiemi di ordine n e k rispettivamente con il:
TEOREMA Detto J l’insieme di suriezioni da un insieme X di ordine
n ad un insieme Y di ordine k . Allora:
J = k ! S ( n, k )
n
n1 , n2 ,..., nk
dove l’ordine dell’insieme J delle suriezioni è: J = ∑
I numeri di Bell
Definizione: Dato un insieme I di ordine n , definiamo numero di Bell
B(n) il numero di tutte le possibili partizioni dell’insieme.
n
Si osserva subito che l’ n -esimo numero di Bell è: B(n) = ∑ S (n, k )
k =1
cioè la somma degli elementi dell’ n -esima riga del triangolo di Stirling.
3
Per calcolare i primi sette numeri di Bell mi limito allora a sommare i
numeri delle sette righe del triangolo riportato in precedenza:
B(1) = 1 , B (2) = 2 , B(3) = 5 , B(4) = 15 , B(5) = 52 , B (6) = 203 , B (7) = 877 .
Con la figura seguente diamo rappresentazione del modo in cui sia
possibile raggruppare 4 elementi in insiemi di ordine 1, 2 3, 4.
La figura conferma i risultati ottenuti per entrambi tipi di numeri, infatti:
S (4,1) = 1
S (4,2) = 7
S (4,3) = 6
S (4,4) = 1
B(4) = 15
Anche i numeri di Bell sono legati da una relazione ricorsiva:
TEOREMA:
Dato un insieme I di ordine n ≥ 1 , siano B(n − i) e B(n) l’ (n − i) -esimo e
l’ n -esimo numero di Bell. Si ha:
n
n − 1
B(n − i ) .
B (n) = ∑
1 i −1
Dimostrazione:
Si consideri P una partizione dell’insieme I .
4
Formula di Aitken
L’elemento a di I appartiene ad uno e uno solo dei sottoinsiemi A di P ;
ciò significa che ogni partizione di I è determinata univocamente dal
sottoinsieme A che contiene a e da una partizione di I − A .
L’ordine i dell’insieme A è compreso tra 1 ed n ( i ≠ 0 perché A ≠ ∅).
n − 1
modi, poiché tanti sono i sottoinsiemi di I
A può essere scelto in
i −1
che contengono a ; le partizioni di I − A , che è un insieme di ordine n − i ,
risultano invece essere B(n − i) . Dunque, per ogni i , con 1 ≤ i ≤ n , vi sono
n − 1
B(n − i ) partizioni di I
esattamente (per il principio delle scelte)
i −1
nelle quali a appartiene ad un elemento A di ordine i .
n
n − 1
B(n − i )
i −1
Ne segue che le partizioni distinte di I sono B(n) = ∑
1
Osservazione: Esistono relazioni ricorsive in cui è possibile calcolare il
termine n -esimo usando soltanto il termine precedente (come nel caso
della successione geometrica e della successione aritmetica) e sono dette
relazioni ricorsive del primo ordine. Se per calcolare il termine n -esimo
utilizzo i due termini che lo precedono (come nella successione di
Fibonacci) ho a che fare con relazioni ricorsive del secondo ordine.
Per calcolare
B(n)
occorre conoscere gli
n
numeri di Bell
B(0) , B(1),..., B(n) ; si dice che la relazione ricorsiva non ha ordine finito.
Esiste una curiosa interpretazione poetica dei numeri di Bell, matematico
ma anche autore di romanzi polizieschi con lo pseudonimo di John Taine.
Si può constatare infatti che B(n) è il numero dei possibili schemi di rima
per una strofa di poesia di n versi.
Riportiamo nella tabella le rime possibili di strofe con valori di n fino a
4 ; quest’ultimo caso rappresenta dunque le possibili rime di una quartina.
5
Esempi celebri relativi alla tabella possono essere ritrovati nella Divina
Commedia; Dante utilizza terzine con rime rappresentate dal quarto tipo:
A
B
A
Nel mezzo del cammin di nostra vita
mi ritrovai per una selva oscura
ché la diritta via era smarrita
e nel Canzoniere, Lorenzo de’Medici fa uso di quartine dell’ultimo tipo:
A
B
B
A
Quant'è bella giovinezza
che si fugge tuttavia!
Chi vuol esser lieto, sia:
di doman non c'è certezza
Sempre nell’ultimo spazio che raffigura le possibili rime delle quartine
abbiamo nel primo esempio la rappresentazione della rima alternata
(schema ABAB) e nell’ottavo la rima baciata (schema AABB)
BIBLIOGRAFIA
-
N.L.Biggs, Discrete mathematics
Ed. Clarendon presse, Oxford 1985
Cerasoli-Eugeni-Protasi, Elementi di matematica discreta
Ed. Zanichelli, Bologna 1988
J.H.Conway-R.K.Guy, The book of numbers Ed. CopernicusSpringer-Verlag 1955
6