Lezione n° 03 1 – Frequenze cumulate

Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
Lezione n° 03
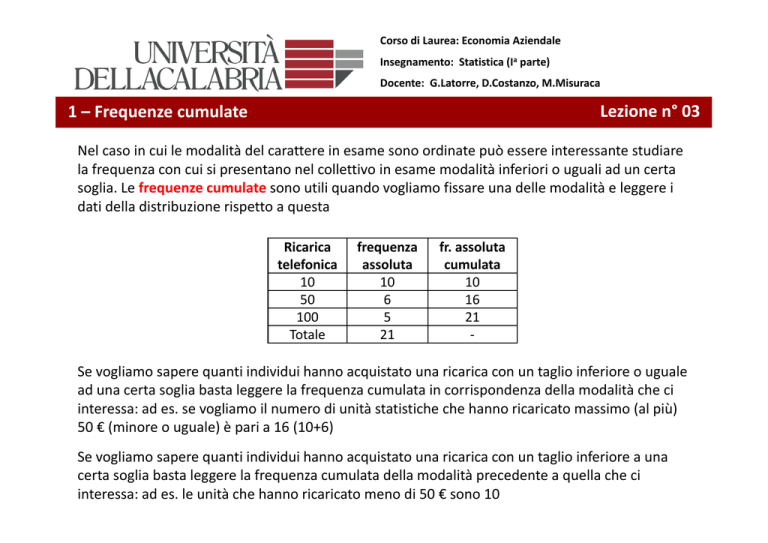
1 – Frequenze cumulate
Nel caso in cui le modalità del carattere in esame sono ordinate può essere interessante studiare N
l
i
il
d lità d l
tt
i
di t
ò
i t
t t di
la frequenza con cui si presentano nel collettivo in esame modalità inferiori o uguali ad un certa soglia. Le frequenze cumulate sono utili quando vogliamo fissare una delle modalità e leggere i dati della distribuzione rispetto a questa
dati della distribuzione rispetto a questa
Ricarica
telefonica
10
50
100
Totale
frequenza
assoluta
10
6
5
21
fr. assoluta
cumulata
10
16
21
‐
Se vogliamo sapere quanti individui hanno acquistato una ricarica con un taglio inferiore o uguale ad una certa soglia basta leggere la frequenza cumulata in corrispondenza della modalità che ci
ad una certa soglia basta leggere la frequenza cumulata in corrispondenza della modalità che ci interessa: ad es. se vogliamo il numero di unità statistiche che hanno ricaricato massimo (al più) 50 € (minore o uguale) è pari a 16 (10+6)
Se vogliamo sapere quanti individui hanno acquistato una ricarica con un taglio inferiore a una Se
vogliamo sapere quanti individui hanno acquistato una ricarica con un taglio inferiore a una
certa soglia basta leggere la frequenza cumulata della modalità precedente a quella che ci interessa: ad es. le unità che hanno ricaricato meno di 50 € sono 10
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
Lezione n° 03
2 – Notazione
È possibile calcolare le frequenze cumulate a partire dalle frequenze assolute, relative o percentuali. Per distinguere le frequenze cumulate vengono indicate con la lettera maiuscola corrispondente
X
N
F
P
x1
N1
F1
P1
x2
N2
F2
P2
…
…
…
…
xi
Ni
Fi
Pi
…
…
…
…
xk
Nk
Fk
Pk
totale
-
-
-
Nel prosieguo indicheremo con:
xi la generica i‐esima modalità del carattere X (con i=1,2,…,k)
Ni la i‐esima frequenza assoluta cumulata delle prime i modalità
Fi la i‐esima frequenza relativa cumulata delle prime i modalità
Pi la i‐esima frequenza percentuale cumulata delle prime i modalità
Ni =
Pi =
i
∑nj
, i = 1,2 ,..., k
j =1
i
∑ pj
j =1
, i = 1,2 ,...,k
Fi =
i
∑ fj
j =1
, i = 1,2 ,...,k
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
3 – I diversi tipi di frequenza (e distribuzione) Lezione n° 03
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
Lezione n° 03
4 – Esercizio
X
n
0
5
1
12
2
19
3
9
4
4
5
1
Totale 50
X
n
0
20
1
10
2
35
3
15
4
10
5
10
Totale 100
COLLEETTIVO B
COLLEETTIVO A
Consideriamo nuovamente i due collettivi di famiglie e le distribuzioni del n° di figli per famiglia
Relativamente al solo collettivo A:
• Quante sono le famiglie che hanno al più un figlio?
• Qual è la percentuale di famiglie che hanno al massimo 2 figli?
• Qual è la percentuale di famiglie che hanno almeno 2 figli?
• Quante sono le famiglie che hanno meno di 3 figli?
• Quante sono le famiglie che hanno non meno di 4 figli?
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
5 – Soluzione
Lezione n° 03
Collettivo A
Collettivo A
X
n N
F
P
0
5 5 0,10 10%
1
12 17 0,34 34%
2
19 36 0,72 72%
3
9 45 0,90 90%
4
4 49 0,98 98%
5
1 50 1 100%
Totale 50 ‐
‐
‐
Calcoliamo innanzi tutto le frequenze cumulate
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
6 – Rappresentazione grafica delle fr. cumulate
Lezione n° 03
Spesso è utile rappresentare graficamente la distribuzione delle frequenze cumulate
In generale è possibile utilizzare un grafico “a gradini” del tipo riportato qui di seguito F(x)
( )
Questo tipo di rappresentazione consente di Questo
tipo di rappresentazione consente di
visualizzare la cosiddetta “funzione di ripartizione empirica”: se ad es. stiamo studiando un carattere di tipo discreto p
potremmo essere interessati alla fr. relativa (o %) di unità del collettivo sulle quali si è osservata una quantità inferiore ad una soglia prefissata
soglia prefissata
1
0,8
0,6
0
0,4
f(X≤6)
0,2
0
X
1
2
3
4
5
6
7
8
9
10
11
12
13
Per rilevare la frequenza basta leggere il dato in corrispondenza del gradino che ci interessa
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
7 – Poligono delle frequenze
Lezione n° 03
Un altro modo per rappresentare le frequenze cumulate è utilizzare il Poligono delle frequenze
Distribuzione delle aziende per n° di addetti
n. di addetti
5
10
15
20
25
30
35
1.00
1.00
0 90
0.90
0 94
0.94
0.86
0.80
ni
6
12
32
27
41
11
8
137
fi
0,04
0,09
0,23
0,20
0,30
0,08
0,06
1,00
Fi
0,04
0,13
0,36
0,56
0,86
0,94
1,00
0.70
0.60
0.50
0.56
0.40
0.36
0.30
0.20
0.10
0.13
0.04
0.00
5
10
15
20
25
30
35
Dall’analisi della tabella e del grafico possiamo immediatamente rilevare che le aziende con meno di 15 addetti sono il 36% del collettivo mentre le aziende con meno di 20 addetti rappresentano
di 15 addetti sono il 36% del collettivo, mentre le aziende con meno di 20 addetti rappresentano complessivamente il 56% del collettivo (ovviamente includendo anche le aziende che ne hanno meno di 15) Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
8 – Esercizio
Lezione n° 03
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
Lezione n° 03
9 – Esercizio
Il responsabile del settore personale del Comune di Cosenza conosce la distribuzione degli impiegati secondo la qualifica funzionale
Qualifica
Impiegati
I
II
III
IV
V
VI
VII
58
308
287
71
52
28
12
816
Il Comune ha bandito un concorso per quattro posti riservati agli interni con qualifica non inferiore alla V
riservati agli interni con qualifica non inferiore alla V
Qual è la percentuale dei possibili candidati al concorso?
Qual è il collettivo statistico e qual è il carattere oggetto di studio?
Come traduciamo in termini statistici il quesito del responsabile del personale?
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
10 – Distribuzione in classi
Lezione n° 03
Quando si analizza un fenomeno che può essere espresso per mezzo di un carattere discreto con numerose modalità, (es. età in anni compiuti) oppure quando si usano caratteri continui
(es. peso, altezza), è possibile che le distribuzioni di frequenza assolute o relative non siano idonee e non migliorino la comprensione dei dati
In questi casi può essere adoperata un’altra rappresentazione dei dati: le modalità (discrete o continue) sono organizzate in intervalli di valori dette classi, e le frequenze associate a ciascun intervallo rappresentano il n° di unità sulle quali è osservato/misurato un valore appartenente all’intervallo stesso
Bisogna dire che se la rappresentazione in classi presenta la stessa facilità di lettura di una
qualsiasi distribuzione di frequenze (assolute o relative) non è però altrettanto immediata e l i i di t ib i
di f
(
l t
l ti )
è
ò lt tt t i
di t
di facile costruzione a partire dalla distribuzione unitaria dei dati. È infatti necessario tenere
in considerazione diversi elementi: il numero di classi adeguato al problema, l’ampiezza delle
diverse classi la possibilità di includere tutte le modalità del carattere e così via
diverse classi, la possibilità di includere tutte le modalità del carattere, e così via
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
11 – Caratteristiche delle classi (1)
Lezione n° 03
‐ In generale una classe può essere vista come un intervallo di valori numerici: ciascuno di questi intervalli deve essere disgiunto, non devono cioè esserci sovrapposizioni, in modo che ogni unità appartenga ad una e una sola classe
‐ L’ampiezza di ciascuna classe può essere costante oppure differente: nel primo caso si parla di
classi equiampie, nel secondo caso si parla di classi non equiampie. La scelta di un tipo dipende talvolta dalle scelte soggettive del ricercatore ma spesso è strettamente legata a fenomeno che
talvolta dalle scelte soggettive del ricercatore ma spesso è strettamente legata a fenomeno che
si vuole rappresentare: CLASSE
Criterio
Da 0 a 5 anni
Età prescolare
Da 6 a 10 anni
Da 6 a 10 anni
Scuola elementare
Scuola elementare
Da 11 a 13 anni
Scuola media
Da 14 a 18 anni
Scuola superiore
…
…
In questo caso la suddivisione in classi del carattere età è dettata da un criterio esterno che fornisce comunque un interessante punto di vista rispetto al tipo di fenomeno che si sta
vista rispetto al tipo di fenomeno che si sta studiando
NB: le classi non devono mai essere vuote (cioè con 0 unità statistiche)
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
12 – Caratteristiche delle classi (2)
Lezione n° 03
È possibile parlare di classi aperte o chiuse a seconda che gli estremi siano inclusi o meno nell’intervallo: la modalità più piccola della classe è detta estremo inferiore, la modalità più grande è detta invece estremo superiore
grande è detta invece estremo superiore
Se l’estremo inferiore è incluso nello classe mentre non lo è quello superiore allora si parla
di classe chiusa a sinistra e aperta a destra; se invece l’estremo inferiore della classe non è p
;
incluso nella classe mentre lo è quello superiore si parla di classe aperta a sinistra e chiusa
a destra. Se includiamo sia l’estremo inferiore che superiore allora parliamo genericamente
di classe chiusa: questo tipo di classi è però idoneo per rappresentare i soli caratteri discreti
La scelta di includere o meno uno degli estremi è univoca: se decidiamo che la prima classe della distribuzione è chiusa a sinistra e aperta a destra (o viceversa), allora tutte le classi della distribuzione saranno dello stesso tipo
distribuzione saranno dello stesso tipo
Un particolare tipo di classi sono quelle non limitate inferiormente o superiormente: in tal caso si utilizza la notazione matematica < (minore di) e > (maggiore di), oppure si ricorre ad esempio (
)
( gg
), pp
p
a locuzioni del tipo “fino a” (<) o “più di” (>)
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
13 – Determinazione del numero di classi
Lezione n° 03
Non esiste un modo univoco per determinare il numero di classi: molte volte, a seconda del fenomeno oggetto di studio, la scelta è lasciata all’esperienza di chi effettua lo studio
La regola da seguire è che non bisogna scegliere un n° di classi eccessivamente piccolo per non perdere dettaglio nella rappresentazione del fenomeno, ma al contempo non bisogna scegliere un n° di classi eccessivamente grande per non “sacrificare” la leggibilità della distribuzione
Nel corso degli anni sono state proposte diverse soluzioni per determinare in modo oggettivo il numero di classi ideale per una popolazione di numerosità pari a N: una possibile soluzione è quella di considerare il numero k di classi ottenuto dalla regola di Sturges
quella di considerare il numero k di classi ottenuto dalla regola di Sturges
k ≅ 1+3,322ilog10 (N)
REGOLA DI STURGES
N° DI CLASSI DA CONSIDERARE
NELLA DISTRIBUZIONE
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
14 – Determinazione dell’ampiezza
Lezione n° 03
Una volta determinato il numero delle classi è necessario stabilire se si vogliono considerare classi di uguale ampiezza o meno
Nel caso in cui si considerano classi di ampiezza diversa bisogna chiaramente procedere ad una Nel
caso in cui si considerano classi di ampiezza diversa bisogna chiaramente procedere ad una
scelta coerente con il fenomeno che si sta analizzando, come illustrato in precedenza con l’esempio della distribuzione per età costruita sulla base del livello scolastico
Se invece si considerano classi di ampiezza uguale allora è necessario trovare un modo per determinare in modo pratico e veloce la quantità che si assume costante per ogni intervallo
Tale quantità può essere ottenuta facilmente considerando l’ampiezza della distribuzione, a partire dalla differenza della modalità più grande e della modalità più piccola osservata nella distribuzione unitaria dei dati e dividendo per il numero di classi definito precedentemente:
x (N) - x (1)
k
≅ω
La lettera omega dell’alfabeto greco è utilizzata per convenzione per indicare l’ampiezza della classe: va
chiaramente approssimata al numero intero più vicino
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
Lezione n° 03
15 – Notazione
In generale una distribuzione in classi per un carattere con k classi distinte si presenta come:
X
n
x1-x2
n1
x2-x3
n2
…
…
xi-1-xi
ni
…
…
xk-1-xk
nk
totale
N
Nel prosieguo indicheremo con:
xi‐1‐xi la generica i‐esima classe di modalità del carattere X (con i=1,2,…,k)
ni la i‐esima frequenza della classe x
la i esima frequenza della classe xi‐1‐xxi
La frequenza indica equivalentemente:
1) il numero di volte che la classe di modalità è stata rilevata sul collettivo
1) il numero di volte che la classe di modalità è stata rilevata sul collettivo
2) il numero di unità statistiche che appartengono ad una classe
k
N=
∑
n i = n 1 + n 2 + ...+ n i + ...+ n k
i= 1
Si legge “sommatoria
Si legge sommatoria per i che va da 1 a k di n con i
per i che va da 1 a k di n con i”
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
16 – Classi aperte e chiuse
Lezione n° 03
IIn generale per indicare se una classe è aperta o chiusa a destra o a sinistra si utilizza la seguente l
i di
l
è
t
hi
d t
i i t i tili l
t
notazione:
xi‐1 ‐| xi oppure (xi‐1 , xi] ‐> la classe è chiusa a destra e aperta a sinistra (le unità che presentano xi‐1
non sono incluse nella classe, quelle che presentano xi invece lo sono)
xi‐1 |‐ xi oppure [xi‐1 , xi) ‐> la classe è aperta a destra e chiusa a sinistra (le unità che presentano xi‐1
sono incluse nella classe, quelle che presentano xi invece non lo sono)
xi‐1 ‐ xi oppure [xi‐1 , xi] ‐> la classe è chiusa a destra e sinistra (sia le unità con xi‐1 che quelle che presentano xi sono incluse nella classe)
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
17 – Rappresentazione dei dati
Lezione n° 03
Una volta ottenute le classi e “contate” quante sono le unità statistiche appartenente ad ogni classe abbiamo di fatto ottenuto una distribuzione di frequenze assolute come quelle viste nelle p
precedenti lezioni, con la differenza che non abbiamo tutte le modalità osservate ma intervalli ,
di modalità
Così come per le distribuzioni di frequenze è possibile leggere in modo differente i dati, ad esempio considerando le frequenze relative o percentuali, oppure calcolando le frequenze cumulate (assolute o relative)
In tutti i casi in cui è necessario effettuare delle operazioni sulle distribuzioni in classe risulta In
tutti i casi in cui è necessario effettuare delle operazioni sulle distribuzioni in classe risulta
difficile ritornare ad una distribuzione di frequenze o unitaria: a tal scopo per convenzione si fa riferimento ad un valore rappresentativo dell’intera classe, detto “valore centrale”, che può esse e ca co ato da a se so
essere calcolato dalla semisomma degli estremi inferiore e superiore di ciascuna classe
a deg est e
e o e e supe o e d c ascu a c asse
estr. inferiore + estr. superiore
= valore centrale
2
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
18 – V. centrale e ampiezza costante
Lezione n° 03
Una volta definito il numero delle classi e l’ampiezza di ciascuna di esse per ottenere gli estremi inferiore e superiore di ciascuna di esse si procede come segue: innanzi tutto è necessario ordinare tutte le modalità in senso crescente, dalla più piccola alla più grande
,
p p
p g
1a classe ‐> x1 ‐|x2 = x1 ‐| x1 + ω
2a classe ‐> x2 ‐|x3 = x1 + ω ‐| x1 + 2ω oppure x2 ‐| x2 + ω
3a classe ‐> x3 ‐|x4 = x1 + 2ω ‐| x1 + 3ω oppure x3 ‐| x3 + ω
…
In generale ‐> x
g
| i = x1 + (i‐1)⋅ω
( ) ‐|x
| 1 + i⋅ω
i 1 ‐|x
i‐1
Quindi una volta individuato l’estremo inferiore della classe è possibile ottenere l’estremo Qu
d u a o ta d duato est e o e o e de a c asse è poss b e otte e e est e o
superiore aggiungendo la quantità relativa all’ampiezza
Per calcolare il valore centrale di ciascuna classe è sufficiente a questo punto aggiungere ad ogni estremo inferiore delle classi la metà dell’ampiezza ω/2
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
19 – Esempio
Lezione n° 03
ω
non eq
quiampie
Consideriamo la seguente distribuzione unitaria
per un collettivo di 200 unità statistiche
ω
equiamp
pie
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
20 – Esercizio
Lezione n° 03
A 150 studenti iscritti al Corso di Laurea Triennale in Economa e Commercio è stato chiesto il Numero di Crediti Formativi ottenendo il seguente elenco grezzo di modalità:
‐ Calcolare il numero di classi
C l l
il
di l i
‐ Costruire delle classi equiampie
chiuse a sinistra
chiuse a sinistra
‐ Calcolare il valore centrale
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
21 – Soluzione
Lezione n° 03
Considerando 150 unità statistiche
possiamo considerare 8 classi
1+3,322
,
ilog
g10 (150)=8,229
(
) ,
Alla luce del numero di classi e dei valori della distribuzione possiamo assumere un’ampiezza pari a 23
11.5
34.5
57.5
80.5
103 5
103.5
126.5
149.5
172.5
valore cen
ntrale
1
0 |‐ 23
2 23 |‐ 46
3 46 |‐ 69
4 69 |‐ 92
5 92 |‐
| 115
6 115 |‐ 138
7 138 |‐ 161
8 161 ||‐ 184
180 - 0
= 22,5
,
8
Calcolate adesso, sulla base della tabella precedente, le frequenze assolute, relative, p
q
e percentuali
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
22 – Uso delle distribuzioni di frequenza
Lezione n° 03
Abbiamo visto come sia possibile dare un’idea efficace e immediata della manifestazione di un fenomeno, in un collettivo, attraverso la costruzione di distribuzioni di frequenza e l’utilizzo delle rappresentazioni grafiche
Nel caso in cui abbiamo tanti dati è spesso più utile la costruzione di una distribuzione di frequenza in classi: perdiamo informazioni ma la lettura è più facile
Codice
intervista
1
2
3
4
5
6
7
8
9
10
ETA’
6
18
10
12
14
35
40
60
25
37
Codice
intervista
11
12
13
14
15
16
17
18
19
20
ETA’
45
50
32
65
72
16
24
38
52
43
Classi di Età
Frequenze ni
6 |‐ 14
6 |
3
14 |‐ 25
4
25 |‐ 40
5
40 |‐ 65
6
>65
2
Totale
20
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
23 – Rappresentazione in classi e grafici
Lezione n° 03
Quando consideriamo una distribuzione di frequenze possiamo rappresentarla graficamente attraverso l’utilizzo di un grafico a torta se ad esempio siamo interessati alla composizione (percentuale) del collettivo in relazione al fenomeno studiato oppure se il carattere è di tipo
(percentuale) del collettivo in relazione al fenomeno studiato, oppure se il carattere è di tipo quantitativo a mettere a confronto l’intensità dei diversi modi di presentarsi del fenomeno (le modalità) attraverso una rappresentazione a barre
Cosa accade nel caso di rappresentazioni statistiche in cui il carattere è sintetizzato mediante l’utilizzo di classi?
Possiamo ancora rappresentare graficamente la composizione del collettivo utilizzando un grafico a torta, ma se vogliamo comparare l’intensità delle diverse modalità del carattere nel collettivo allora è necessario prendere in considerazione il fatto che le classi possano avere la
collettivo allora è necessario prendere in considerazione il fatto che le classi possano avere la stessa ampiezza o essere di ampiezza diversa: in questo secondo caso infatti vogliamo tener conto del fatto che un carattere si sia potuto manifestare in un certo modo in una classe più
o meno ampia, perché questo ha di fatto ha una diversa interpretazione
p ,p
q
p
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
24 – L’istogramma
Lezione n° 03
Lo strumento grafico utilizzato per visualizzare le distribuzioni di frequenze in classi è il cosiddetto istogramma: sull’asse orizzontale sono rappresentate le classi, su quello verticale è invece espressa l’intensità del fenomeno (in termini di frequenza assoluta, relativa o %)
10
50%
8
40%
6
30%
4
20%
2
10%
0
0%
10
30
50
70
90
10
30
50
70
90
L’area di ciascuna barra sarà proporzionale all’intensità: la proporzione ovviamente è la stessa
sia che l’intensità è misurata con le frequenze assolute che l’intensità è espressa, ad esempio, in termini percentuali. Le barre non sono tra loro distanziate per dare un’idea di continuità nella rappresentazione del carattere
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
25 – Istogramma per classi non equiampie
Lezione n° 03
Nel caso di classi con ampiezza diversa è ancora possibile l’utilizzo dell’istogramma come rappresentazione grafica
In questo caso assume però un significato differente il fatto che l
In
questo caso assume però un significato differente il fatto che l’intensità
intensità in una specifica in una specifica
classe sia maggiore o minore, perché i possibili valori osservati sulle unità statistiche sono “pochi” o “molti” a seconda che l’ampiezza della classe sia minore o maggiore
Densiità di frequenzza
Per poter allora ottenere delle barre proporzionali all’intensità espressa nella classe e allo stesso tempo considerare
classe, e allo stesso tempo considerare l’ampiezza della stessa, si utilizza come misura dell’intensità non più la frequenza ma la cosiddetta densità di frequenza :
f q
Area = base x altezza
Classi di età
Area ‐> frequenza
base ‐> ampiezza
altezza ‐> densità di frequenza
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
26 – Esempio
Lezione n° 03
4
ni
Ni
fi
Fi
di
15 ‐| 20
4
4
0,4
0,4
0,08
20 ‐| 25
3
7
0,3
0,7
0,06
25 | 30
25 ‐|
1
8
01
0,1
08
0,8
0 02
0,02
30 ‐| 35
2
10
0,2
1
0,04
10
3
2
1
1
0
15
20
25
30
35
Leggendo i dati in tabella e nel grafico corrispondente si rileva come ci sia una maggiore incidenza della classe 15 ‐| 20 : tale aspetto è verificato anche dalle frequenze relative e
dalle densità di frequenza, dal momento che tutte le classi hanno la stessa ampiezza
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
classi di età
0 ‐| 5
5 ‐| 15
|
15 ‐| 30
30 ‐| 35
Lezione n° 03
amp. classe
5
10
15
5
freq. %
17,0
40,0
,
37,0
6,0
densità
3,4
4,0
,
2,5
1,2
Dall’analisi della tabella si vede come la frequenza percentuale più alta sia stata osservata in corrispondenza della classe
di età 5 | 15: ciò vuol dire che le unità
di età 5 ‐| 15: ciò vuol dire che le unità statistiche che hanno una età tra i 5 e i 15 anni sono quelle più presenti
Densitàà di frequenza
27 – Esempio
Classi di età
Se consideriamo le classi 0 ‐| 5 e 15 ‐|30 osserviamo che sono rispettivamente la terza e la seconda classe più osservata: calcolando però le densità di frequenza vediamo che in realtà, tenendo conto della diversa ampiezza delle classi la classe 0 ‐| 5 è della diversa ampiezza delle classi, la classe 0 ‐| 5
è “più
più importante
importante” della classe 15 ‐|30
della classe 15 ‐|30 perché le perché le
unità statistiche sono meno disperse, cioè assumono meno valori rispetto a quelli dell’altra classe
Corso di Laurea: Economia Aziendale
Insegnamento: Statistica (Ia parte)
Docente: G.Latorre, D.Costanzo, M.Misuraca
Docente: G.Latorre, D.Costanzo, M.Misuraca
28 – Altri utilizzi degli istogrammi
Lezione n° 03
È possibile accoppiare due istogrammi, rappresentanti ad esempio la misura di un fenomeno quantitativo su due sottopopolazioni omogenee per una certa caratteristica, in modo da avere una idea immediata delle diverse intensità nei due gruppi
Popolazione straniera residente in Italia – 2001 (ISTAT)
Esempio – Piramide delle età
Esempio Piramide delle età
> 90
85 ‐ 89
80 ‐ 84
75 ‐ 79
70 ‐ 74
65 ‐ 69
60 64
60 ‐
55 ‐ 59
50 ‐ 54
45 ‐ 49
40 ‐ 44
35 ‐ 39
30 ‐ 34
25 29
25 ‐
20 ‐ 24
15 ‐ 19
10 ‐ 14
5 ‐ 9
0 ‐ 4
MASCHI
FEMMINE
Tale rappresentazione è usata soprattutto nello studio per età delle popolazioni: è possibile rilevare ad esempio, oltre alla composizione, i momenti storici d
durante i quali ci sono state delle i
li i
d ll
flessioni o degli aumenti delle nascite
1
15
10
5
0
5
10
1
15