ESAME DI STATO DI LICEO SCIENTIFICO 2003-2004
Corso Sperimentale P.N.I.
Tema di MATEMATICA - 17 giugno 2004
Svolgimento a cura della prof.ssa Sandra Bernecoli e del prof. Luigi Tomasi
([email protected])
RISOLUZIONE DEI QUESITI DEL QUESTIONARIO
Quesito n. 1
Si definisce grado sessagesimale la 360a parte dell’angolo giro.
Si definisce angolo radiante l’angolo i cui lati intercettano su una qualunque circonferenza, con
centro nel suo vertice, un arco che, rettificato, è lungo come il raggio.
Si definisce “grado” centesimale la 400a parte dell’angolo giro.
Per le definizioni delle unità di misura degli angoli si rinvia ad un buon libro di matematica (o di
fisica), anche se non sempre nei libri vengono citati i gradi centesimali (simbolo sulla calcolatrice:
GRAD), pur essendo presenti in tutte le calcolatrici scientifiche e nei software di geometria che
hanno degli strumenti dedicati alla misura degli angoli.
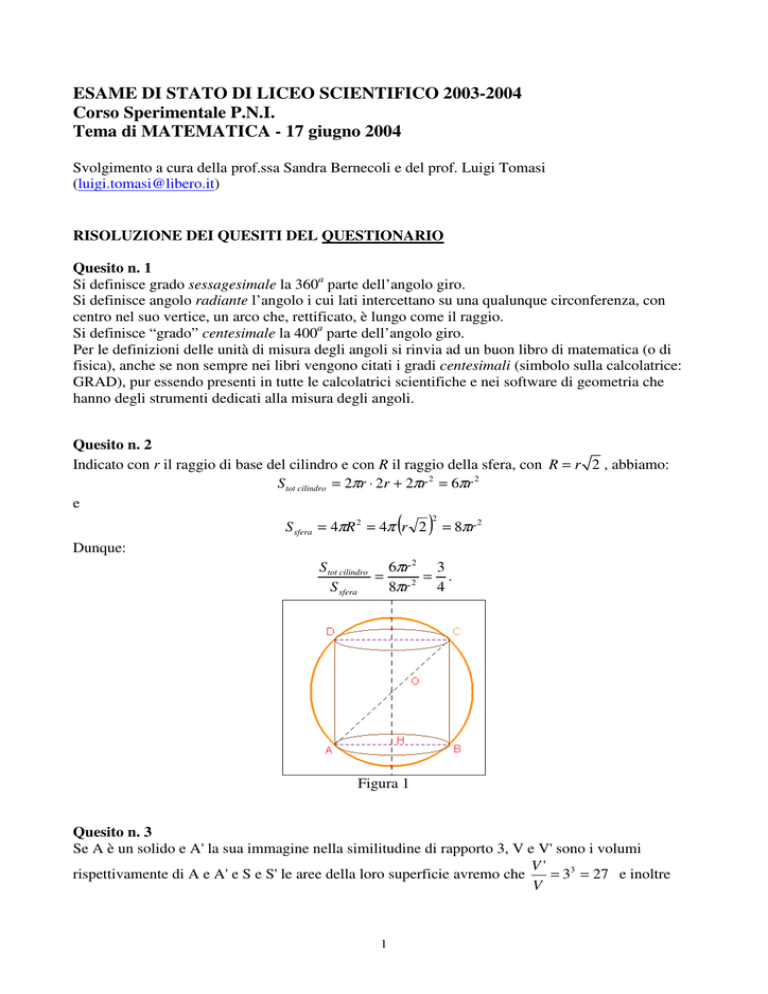
Quesito n. 2
Indicato con r il raggio di base del cilindro e con R il raggio della sfera, con R = r 2 , abbiamo:
S tot cilindro = 2πr ⋅ 2r + 2πr 2 = 6πr 2
e
( )
S sfera = 4πR 2 = 4π r 2
2
= 8πr 2
Dunque:
S tot cilindro 6πr 2 3
=
= .
S sfera
8πr 2 4
Figura 1
Quesito n. 3
Se A è un solido e A' la sua immagine nella similitudine di rapporto 3, V e V' sono i volumi
V'
rispettivamente di A e A' e S e S' le aree della loro superficie avremo che
= 33 = 27 e inoltre
V
1
S'
= 32 = 9 . La dimostrazione si può fare per uno dei solidi notevoli anche se è valida in generale.
S
Quesito n. 4
Dati gli insiemi A ={1, 2, 3, 4} e B = {a, b, c}, le applicazioni di A in B sono 34 = 81 .
Infatti ci saranno 3 scelte per f (1) e, per ciascuna di queste, 3 scelte per f (2) e quindi 3 scelte per
f (3) e poi 3 scelte per f (4) .
In totale si hanno 3 ⋅ 3 ⋅ 3 ⋅ 3 scelte e quindi 34 = 81 funzioni. Si tratta delle disposizioni con
ripetizione di 3 oggetti di classe 4.
Quesito n. 5
Una funzione, che soddisfa alla richiesta, potrebbe essere così definita:
( x + 1)( x − 2 )
se x ≠ 2
g ( x) = (x − 2 )
4
se x = 2
g ( x) è una funzione che ammette nel punto x=2 una discontinuità detta si solito di “terza specie” o
“eliminabile”.
Quesito n. 6
Ovviamente le funzioni che soddisfano alle richieste sono infinite. Volendo utilizzare una cubica, la
sua derivata prima dovrà avere del tipo: f ' ( x) = a 1 − x 2 , con a > 0 . Integrando si ha pertanto
1
f ( x) = ax − ax 3 + c . Imponendo il passaggio per i punti assegnati M(1,3) e N(−1,2), si ottiene:
3
1 3 3
5
f ( x) = − x + x + .
4
4
2
(
Figura 2
2
)
Quesito n. 7
Se i triangoli hanno base assegnata AB e la stessa area allora avranno anche la stessa altezza e
quindi il vertice C apparterrà a una retta r parallela alla retta di AB e a distanza da AB pari
all'altezza.
Figura 3
Sia A' il punto simmetrico di A rispetto alla retta r. Consideriamo il triangolo ABC’ (figura 3). Il
perimetro sarà minimo quando AC’+C’B sarà minimo, dal momento che AB è costante.
La retta r è l’asse del segmento AA'. Quindi AC=A'C e pertanto
AC’+C’B=A'C’+C’B ≥ A'B
(la somma di due lati di un triangolo è sempre maggiore o uguale al terzo lato).
Il triangolo ABC’ avrà perimetro minimo quando i tre punti A', C’, B sono allineati, ossia quando il
punto C’ coincide con C e il triangolo ABC è isoscele.
Quesito n. 8
Siano a, b due numeri reali con a ≠ b.
Si sa che a + b = p e ab = p ; a e b saranno le soluzioni dell'equazione di secondo grado
z 2 − pz + p = 0 .
Risolvendola, ponendo la condizione che p( p − 4) > 0 (non si possono accettare i valori p = 0 e
p = 4 perché in tali casi si avrebbe a = b , contro l’ipotesi), si ottengono le soluzioni:
p( p − 4 )
p + p( p − 4 )
e z2 = b =
.
2
2
A questo punto si possono ottenere delle coppie di numeri che soddisfano alle condizioni poste. La
richiesta contenuta in questo quesito è molto generica. Quindi si poteva anche rispondere in modo
a
più semplice, ad esempio ponendo a + b = ab e ricavando quindi che b =
(con a ≠ 1 ).
a −1
3
Sostituendo in modo opportuno, ad esempio a = 3 , si ha b = .
2
z1 = a =
p−
Quesito n. 9
y = ex
L’equazione e + 3x = 0 è equivalente al sistema
; rappresentandolo graficamente si
y = −3 x
deduce che l’equazione data ammette una e una sola soluzione negativa in [−1, 0].
x
3
Figura 4
Si consideri la funzione f ( x) = e x + 3 x . Poiché f ' ( x) > 0 per ogni x del dominio, la funzione è
strettamente monotona crescente e dal momento che lim f ( x) = +∞ e inoltre lim f ( x) = −∞
x→+∞
x→−∞
ed essendo la funzione continua, intersecherà l'asse delle x una sola volta. Applicando il metodo di
bisezione nell’intervallo [−1, 0], si trova che la radice vale circa x = −0,257... .
Quesito n. 10
Possiamo scrivere la trasformazione nel seguente modo:
x := x 3 − y
y := x + y 3
3 − 1
La matrice della trasformazione è M =
. La trasformazione data è una similitudine che
3
1
ha l’origine degli assi O come punto unito. Il determinante della matrice è det M = 4 ; la
similitudine è quindi diretta ed ha rapporto k = 2 .
4
Figura 5
Possiamo riscrivere le due equazioni in questo modo:
3 1
− y
x := 2 x
2
2
1
3
x+ y
y
:
=
2
2
2
ossia
π
π
x := 2 x cos − y sin
6
6
y := 2 x sin π + y cos π
6
6
Da queste ultime equazioni si ricava pertanto che la trasformazione è la composizione di una
rotazione di π/6 di centro l'origine con una omotetia di centro l'origine e rapporto 2. Ritroviamo
quindi, anche in questo modo, che la trasformazione è una similitudine di rapporto 2.
5












