Kepler

http://www.fisicamente.net/index-1563.htm ( per consultare il saggio completo)
JOHANN KEPLER
Kepler (1571 - 1630) nacque a Weil der Stadt in Württemberg nel 1571. La sua
famiglia era protestante e di modeste condizioni economiche. Dal 1579 studiò a Tubinga
dove divenne un seguace di Copernico. La tentazione dell'epoca di seguire una carriera
ecclesiastica fu rifiutata da Kepler perché si rese immediatamente conto della ristrettezza
delle visuali del clero luterano. Scelse lo studio della scienza accettando (1594) l'incarico
di soprintendente di matematica della Stiria ed insegnò a Graz (ma sembra che la
matematica non fosse il suo forte: gli alunni disertavano le sue lezioni), "arrotondando",
come quasi tutti gli astronomi dell'epoca, facendo oroscopi e predizioni (e poiché
qualche predizione si avverava, venne preso in considerazione come buon astrologo).
Nel 1595, all'età di 24 anni, pubblicò la sua prima opera, il "Mysterium
Cosmographicum", con la quale credette di aver svelato i segreti del sistema planetario.
In realtà ciò che aveva fatto era la scoperta che vi sono una mole di ragioni per
abbandonare il sistema tolemaico e per abbracciare quello copernicano, ragioni però
molto tecniche che non rappresentavano comunque alcuna "prova", almeno agli occhi
del grande pubblico. Il Mysterium fu mandato sia a Tycho che a Galileo ma aveva un
grave difetto, soprattutto se visto con gli occhi di un personaggio che è uscito dalle
pastoie del misticismo, della numerologia, della magia, dell'animismo e dell'ermetismo:
è intriso di tutte le cose dette in modo esasperato, tanto che oggi ci vuole davvero uno
sforzo di ottima volontà a rintracciare i contributi scientifici originali, che pure vi sono.
Un esempio lampante di ciò che dico è il breve rapporto epistolare che Galileo
intrattenne con Kepler. Si scrissero nel 1597 (mentre Galileo si trovava a Padova);
ambedue confidarono il loro essere copernicani; Kepler apertamente, Galileo titubante
perché non si azzardava ad avanzare una qualche teoria senza avere delle sensate
esperienze e dimostrazioni a sostegno di essa. Ma la lettura di queste lettere,
specialmente quella di Galileo a Kepler dell'agosto 1597 (in cui Galileo si mostra
entusiasta del lavoro di Kepler) e quella di Kepler a Galileo dell'ottobre dello stesso
anno, mostra due caratteri diversi, Galileo che faticosamente tentava di uscire dal 1500,
Kepler che, pur muovendosi con idee "moderne", era pienamente impantanato in quel
clima. Sta di fatto che Galileo provava quasi fastidio a leggere gli scritti del suo collega,
noiosi, contorti, difficili e prolissi, scritti dai quali si faceva una enorme fatica a ricavare
qualcosa di utile. Vi sono inoltre moltissimi calcoli errati che poi si sistemano
compensandosi fortunosamente. La differenza tra i due si nota facilmente leggendo un
qualunque brano di Kepler e confrontandolo con un qualunque brano di Galileo. E
questo anche per rispondere a qualche critico che, oggi, rimprovera a Galileo di non aver
tenuto conto dell'ellitticità delle orbite planetarie che Kepler aveva scoperto.
Ma veniamo ad alcune delle cose che fanno da spessa cornice ai contributi
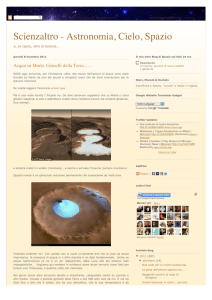
scientifici di Kepler. Innanzitutto la mistica dei numeri governa il mondo. Si tratta di
immaginare un mondo di orbite che si incastrano alternativamente con i cinque solidi
regolari (vedi figure). Si inizia con la sfera di Saturno che è circoscritta ad un cubo; nel
cubo è inscritta la sfera di Giove che, a sua volta, è circoscritta ad un tetraedro; questo
tetraedro è circoscritto alla sfera di Marte che, a sua volta, è inscritta in un dodecaedro;
al dodecaedro, per circoscrizioni ed inscrizioni successive, segue la sfera della Terra,
l'icosaedro, la sfera di Venere, l'ottaedro, la sfera di Mercurio, quindi il Sole al centro
dell'intero sistema (si osservi che, per permettere l'eccentricità delle orbite ellittiche che
Kepler scopre, occorre ammettere che ogni sfera abbia uno spessore tale da poter
contenere appunto l'eccentricità dell'orbita).
Dal Mysterium Cosmographicum (II edizione, Tubinga 1597). In alto a destra è riportata in dettaglio la parte più
interna della figura grande.
Un disegno che mostra le successive inscrizioni di solidi regolari e sfere
Da Harmonices mundi
I conti, con i dati osservativi di Copernico e, soprattutto, con l'enorme mole di quelli
di Tycho, gli tornavano in modo abbastanza approssimato. È poi interessante osservare
che anche numero di pianeti e di solidi erano in accordo. Ancora non si conoscevano i
pianeti al di là di Saturno. E mentre i pianeti sono cresciuti di numero, i solidi regolari
sono restati 5. Ma tant'è. Egli diceva:
Io mi impegno a dimostrare che Dio, nel creare l'Universo e nel regolare l'ordine del
cosmo, aveva in vista i cinque corpi regolari della geometria, così come sono conosciuti
dai tempi di Pitagora e Platone, e che Egli ha stabilito, in accordo con le loro
dimensioni, il numero dei cieli, le loro proporzioni e le relazioni dei loro movimenti.
Ed in accordo con Pitagora e Platone vi è una visione dell'Universo intrisa di
misticismo. Il Sole è Dio Padre e per questo merita di stare al centro dell'Universo; la
Sfera delle stelle è il Figlio mentre l'Etere, attraverso cui lo spirito del Sole muove i
pesanti pianeti, è lo Spirito Santo. Inoltre, riprendendo temi che già erano stati di Hermes
Trismegisto e Marsilio Ficino, afferma:
Il Sole è il corpo più bello, è l'occhio del mondo. In quanto fonte della luce o lanterna
risplendente, adorna ed abbellisce gli altri corpi del mondo... Per quanto riguarda il
calore, il Sole è il focolare del mondo... La sfera delle stelle fisse trattiene il calore
affinché non si disperda ed è simile ad una parete, ad una pelle o ad un abito del
mondo... Il Sole è l'unico luogo che noi giudicheremmo degno di Dio altissimo, qualora
egli si compiacesse di avere una dimora materiale e scegliesse un luogo in cui abitare
con gli angeli benedetti... Il Sole è l'unico luogo degno di diventare la casa di Dio.
Ma i numeri e la geometria forniscono a Kepler argomenti contro l'infinità dei mondi
sostenuta da Bruno. Dice Kepler:
La geometria è una ed eterna, splendente nella mente di Dio... Nella geometria poi,
dopo la sfera vi è una famiglia di figure che è la più perfetta di tutte, quella dei cinque
corpi solidi euclidei. Ebbene questo nostro mondo planetario è disposto secondo la
regola ed il modello di questi solidi [descritti più su]... A quale scopo sarebbero infiniti,
se ciascuno racchiudesse in sé ogni perfezione [come questo nostro] ?"
Il Libro V di "Harmonices Mundi", che Kepler pubblicò nel 1619 e che contiene
l'enunciato della sua terza legge, ha questo indice:
1 - Sulle cinque figure solide regolari.
2 - Sulle affinità tra esse ed i rapporti armonici.
3 - Compendio sulla dottrina astronomica necessaria per speculare sulle armonie
celesti.
4 - In quali cose pertinenti ai moti planetari le semplici consonanze sono state espresse e
che tutte quelle consonanze che sono presenti nel canto si trovano nei cieli.
5 - Che le chiavi della scala musicale, o gradi del sistema, e i generi delle consonanze, il
maggiore e il minore, sono espressi in certi moti.
6 - Che i singoli Toni e Modi musicali sono in qualche modo espressi dai singoli pianeti.
7 - Che i contrappunti o armonie universali di tutti i pianeti possono esistere ed essere
diversi l'uno dall'altro.
8 - Che i quattro tipi di voci sono espressi nei pianeti; soprano, contralto, tenore e
basso.
9 - Dimostrazione che al fine di garantire questa armonica disposizione, quelle vere
eccentricità planetarie che qualunque pianeta ha come proprie, e non altre, devono
essere stabilite.
10 - Epilogo relativo al Sole, per mezzo di molto fertili congetture.
Una pagina di Harmonices Mundi
Un oroscopo fatto da Kepler
E tutta questa impalcatura musicale gli serve per mostrare che i pianeti ruotando
intorno al Sole, cantano le lodi del Signore. È un canto eterno ed intonato. Noi non
riusciamo a sentirlo ma esso è dato dai rapporti speciali che esistono tra velocità e
distanze dei pianeti dal Sole. Ogni pianeta ha una sua melodia (vedi figura) e la Terra, in
particolare percorre la sua orbita intonando eternamente un MI-FA-MI e da questo
Kepler conclude che "da questo si può capire che la MI-seria e la FA-mine regnano
dovunque in questo mondo".
La scrittura delle note da parte di Kepler in Harmonices Mundi
Da I. B. Cohen. La traduzione delle note precedenti nei simboli a noi noti.
L'universo di Kepler resta finito e sostanzialmente aristotelico, nonostante le
fondamentali novità introdotte e di cui dirò alla fine di questo scritto.
Concludo questa parte relativa al tormentato misticismo di Kepler con due
considerazioni che fece nel 1610 quando fu informato della scoperta di Galileo dei
satelliti di Giove. Inizialmente ebbe un sussulto ed esclamò: "Che abbia avuto ragione
Bruno?". Quindi scrisse: "Perché [tali satelliti] dovrebbero ruotare intorno a Giove se
su questo pianeta non vi è nessuno a contemplare tale spettacolo?".
Ma torniamo alla succinta biografia del nostro astronomo. Lo avevamo lasciato con la
pubblicazione del Mysterium nel 1595. Nel 1598 l'Arciduca Ferdinando d'Austria, dopo
un pellegrinaggio a Loreto, iniziò una campagna di persecuzione contro i protestanti.
Kepler, cacciato dalla Stiria, fuggì e si rifugiò a Praga, luogo dove Tycho esercitava
come matematico imperiale al servizio di Rodolfo II di Bohemia. Nel 1600 Tycho lo
chiamò a Praga perché gli facesse da assistente. Un anno dopo Tycho moriva e lasciava
a Kepler l'enorme eredità di tutti i suoi manoscritti di dati osservativi. Nel 1602, Rodolfo
II lo nominò al posto di Tycho (alla cui memoria fu sempre fedele, anche se Galileo non
si mostrò d'accordo con questo).
A parte una piccola opera di ottica del 1604 (Ad Vitellionem paralipomena), Kepler
lavorava intensamente ad elaborare i dati di Tycho e nel 1609 pubblicò Astronomia
Novaseu Physica coelestis (la parola greca che è nel titolo significa che
egli non si accontenta di una descrizione cinematica ma intende ricercare anche le cause
che producono i fenomeni celesti), opera nella quale, dallo studio delle posizioni di
Marte, ricava le prime sue due leggi (orbite ellittiche e costanza della velocità aereolare)
solo in questo ambito ristretto.
(1ª legge) Le orbite dei pianeti sono delle ellissi di cui il Sole occupa uno dei due fuochi
(questa legge fu stabilita da Kepler nel 1605).
(2ª legge) Le aree spazzate dal segmento che unisce un pianeta con il Sole (raggio
vettore) sono proporzionali ai tempi impiegati a spazzarle (questa legge fu la prima ad
essere trovata da Kepler nel 1602).
E' interessante notare che Kepler studiò per molti anni i suoi dati su Marte perché le
osservazioni non si accordavano con nulla ed in particolare facevano vacillare per intero
il sistema di Tycho. Ma la sua guerra con Marte la vinse proprio con la scoperta delle
due leggi precedenti. Fu successivamente che Kepler si rese conto che queste leggi
funzionavano bene anche per gli altri pianeti, con il riconoscimento della correttezza non
già del sistema di Tycho ma di quello di Copernico. Riguardo alla scoperta delle orbite
ellittiche, le cose stanno pressappoco così. Kepler aveva iniziato con criticare Copernico
per non aver fatto coincidere il centro dell'universo con il Sole. Egli riteneva che la forza
che muoveva i pianeti provenisse da lì e quindi quello dovesse essere il centro. Ma con
alcune misure si rese conto che il centro esatto non era il Sole S ma un centro C spostato
(poi individuato come uno dei fuochi dell'ellisse). A questo punto Kepler credeva ancora
ad un orbita circolare. Ma i dati lo portavano a sistemare il centro della circonferenza in
C e non in S. Il problema era il seguente: perché i pianeti ruotano intorno a C se la forza
che li muove procede da S ? Fu qui che Kepler escogitò la soluzione, supponendo che
ogni pianeta fosse soggetto a due influenze
contraddittorie: da una parte la forza del Sole ed un altra che doveva essere localizzata
nel medesimo pianeta. La concomitanza delle due influenze faceva sì che il pianeta
alcune volte si avvicinava ed altre si allontanava dal Sole. Proseguendo in queste
considerazioni e con la convinzione che dal Sole emana la forza principale che muove i
pianeti, esso doveva agire con maggiore forza sul pianeta quando esso era più vicino e
minore quando era più lontano con conseguenze sulle velocità del pianeta, maggiori a
più piccola distanza e viceversa. E furono queste ultime considerazioni che Kepler poté
verificare con le osservazioni, dalle quali uscì fuori per prima la seconda legge. E questo
sembrava più accettabile della distruzione delle circonferenze, anche se, lungo il lungo
cammino della Astronomia Nova, alla fine del capitolo 44, deve ammettere che l'orbita
di Marte è ovale. E su questo ovale lottò ancora mesi. Finché il 4 luglio 1603 non scrisse
all' amico Fabricius queste parole: se la forma fosse semplicemente una ellisse perfetta,
tutte le risposte potrebbero stare nei lavori di Apollonio ed Archimede. Ma dovette
ancora lavorare molto per riuscire a trovare una legge matematica che descriveva il moto
di Marte intorno al Sole. Ci riuscì dopo anni di interminabili calcoli anche se non si rese
conto che quella formula descriveva proprio un'ellisse. Per ironia della sorte questa
formula fu rifiutata da Kepler che fece tabula rasa di tutto e ricominciò i suoi calcoli a
partire dall'ipotesi che l'orbita fosse ellittica ! Dopo altro periodo di lavoro (in totale 4
anni) si accorse che dove era arrivato era proprio a quella formula che aveva rifiutato.
Nel 1610 scrisse Dissertatio cum Nuntio Sidereo. Accoglieva con entusiasmo i lavori
di Galileo ma, come già detto, non lo convincevano i satelliti di Giove. Sempre nello
stesso anno, nella "Narratio", dopo varie osservazioni al telescopio, darà ragione
completa a Galileo.
Nel 1611 scrisse la Diottrica.
Nel 1615 scrisse la Stereometria doliorum, un trattato sulla cubatura delle botti che
darà un certo impulso a ricerche di analisi infinitesimale.
Tra il 1618 ed il 1620 pubblicò il ponderoso Compendio di astronomia copernicana
nel quale estese le sue due prime leggi a tutti i pianeti. È da notare che questo libro sarà
messo all'Indice nel 1632, in occasione del Processo a Galileo. Solo nel 1821 fu tolto da
tale Indice.
Nel 1619 pubblicò un trattato sulle comete ma, soprattutto, le Harmonices Mundi in
cui è enunciata la sua terza legge che mette in relazione periodi di rotazione dei pianeti
intorno al Sole con distanze di essi dal Sole medesimo.
(3ª legge) I quadrati dei tempi T, impiegati dai pianeti a percorrere la loro orbita, sono
direttamente proporzionali ai cubi dei semiassi maggiori delle ellissi descritte dai
pianeti.
Nel 1627 pubblicò le Tavole Rudolfine, che sostituiranno definitivamente le
precedenti e che per circa 100 anni saranno la bibbia di astronomi e naviganti.
Quest'ultima opera vide la luce ad Ulm. Prima che in questa città egli aveva soggiornato
a Linz ma anche da lì dovette fuggire a seguito di ulteriori persecuzioni di protestanti da
parte dei cattolici. Le peregrinazioni che dovette affrontare in quell'epoca per tentare di
vedere riconosciuti dei suoi diritti gli minarono la salute. Si spense nel 1630 a
Regensburg (Baviera). Ma qui già siamo in epoca moderna nella quale opera o sta per
operare: Galileo, Descartes, Huygens, Leibniz, Newton, .... Dal Seicento la scienza
ricomincia ad acquistare autorità e a diventare motore di progresso civile e morale
nonostante gli ostacoli, a volte criminali, delle varie chiese del mondo.
È doveroso ricordare che Kepler contribuì molto ad eliminare dal sistema
copernicano molte difficoltà e stonature che rappresentavano ancora un retaggio delle
filosofia aristotelica e della cosmologia tolemaica. Come Tycho mise in dubbio
l'esistenza delle sfere che sostengono i pianeti e iniziò a parlare di "orbite" ed aggiunse
anche il fatto che nell'universo non si hanno moti uniformi. Fu il primo a capire che era
necessario individuare una causa che rendesse conto di questo moto dei pianeti su
determinate orbite, oltre ad aver capito (ed iniziato con ciò ad eliminare le pitagoricoplatoniche circonferenze) l'esistenza di orbite ellittiche.