L`effetto Hall quantistico

1
UNIVERSITÀ DEGLI STUDI DI CAGLIARI
Facoltà di Scienze
Corso di laurea in Fisica
L’effetto Hall quantistico
Relatore:
Candidato:
Prof. Michele Saba
Ilaria Pintus
Anno accademico 2015/2016
2
3
Sommario
L’effetto Hall quantistico è un’eccezionale scoperta della fisica della materia condensata. Tale fenomeno si
riscontra in sistemi elettronici a dimensionalità ridotta in cui gli effetti quantistici della materia risultano
fondamentali. L’effetto si manifesta infatti in un gas di elettroni confinato in due dimensioni, tipicamente
un’eterogiunzione a semiconduttore, come quella 𝐺𝑎𝐴𝑠 − 𝐴𝑙𝐺𝑎𝐴𝑠 che descriveremo all’interno di questo
lavoro di tesi. Tali sistemi sono sottoposti a campi magnetici intensi dell’ordine del Tesla e temperature di
frazioni o pochi Kelvin. Sostanzialmente l’effetto Hall quantistico consiste nella quantizzazione della
resistenza trasversa , detta resistenza Hall 𝑅𝐻 , e nell’annullamento della resistenza longitudinale. Trattando il
sistema dal punto di vista quantistico, con un modello a elettroni non interagenti, si dimostra che il campo
magnetico perpendicolare all’interfaccia genera una quantizzazione dei livelli energetici simile a quella di un
oscillatore armonico. I livelli energetici sono detti livelli di Landau e presentano tutti la stessa degenerazione.
L’effetto fu osservato sperimentalmente per la prima volta, e quindi scoperto, nel 1980 dal fisico tedesco
Klaus von Klitzing che per questo fu insignito del premio Nobel per la fisica nel 1985. I suoi risultati vennero
raccolti e pubblicati nell’Agosto del 1980 in una Physical Review Letters, a cui si farà riferimento in questo
lavoro.
Precisiamo che nella trattazione seguente le grandezze vettoriali saranno indicate per comodità con caratteri
in grassetto e l’effetto Hall quantistico sarà abbreviato con l’acronimo inglese QHE.
4
Indice
Capitolo 1
Introduzione . . . . . . . . . . . . . . . . . . . . 5
1.1 L’effetto Hall classico . . . . . . . . . . . . . . . . . . . 5
1.2 Il modello di Drude . . . . . . . . . . . . . . . . . . . . 5
1.2.1 Resistività e resistenza di Hall . . . . . . . . . . . . . 8
1.3 La scoperta del QHE . . . . . . . . . . . . . . . . . . . . 8
Capitolo 2
Sistemi elettronici bidimensionali . . . . . . . . . . . . 10
2.1 Il moto elettronico in meccanica quantistica . . . . . . . . . 10
2.1.1 Hamiltoniana per elettroni non interagenti . . . . . . . 10
2.1.2 Gauge simmetrica . . . . . . . . . . . . . . . . . 11
2.2 Livelli di Landau . . . . . . . . . . . . . . . . . . . . . 12
2.2.1 Degenerazione dei livelli e autostati del sistema . . . . . 13
2.3 Condizione di quantizzazione e fase di Aharonov-Bohm . . . . 16
2.4 Moto in un campo elettrico esterno e gauge di Landau . . . . . 17
2.5 Effetti delle impurità . . . . . . . . . . . . . . . . . . . 19
Capitolo 3
L’effetto Hall quantistico intero IQHE . . . . . . . . . . . . 22
3.1 Realizzazione di sistemi elettronici bidimensionali . . . . . . . 22
3.1.1 Primi esperimenti: sistema Si MOS . . . . . . . . . . 22
3.1.2 L’eterogiunzione GaAs-AlGaAs . . . . . . . . . . . . 24
3.2 Precisione nelle tecniche di misura . . . . . . . . . . . . . 25
3.3 Effetti di bordo . . . . . . . . . . . . . . . . . . . . . . 25
3.3.1 Moto elettronico ai bordi del sistema . . . . . . . . . . 26
3.3.2 Distribuzione della corrente ai bordi del sistema . . . . . 26
3.4 Effetti della temperatura . . . . . . . . . . . . . . . . . . 37
Conclusioni . . . . . . . . . . . . . . . . . . . . 30
Bibliografia . . . . . . . . . . . . . . . . . . . . 31
Elenco figure . . . . . . . . . . . . . . . . . . . 32
Ringraziamenti . . . . . . . . . . . . . . . . . . . 33
5
Capitolo 1
Introduzione
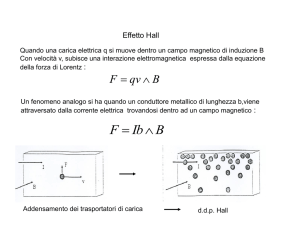
Nel 1879 il fisico statunitense Edwin Hall, indagando sulla natura dei portatori di carica in un metallo,
osservò per la prima volta un effetto del materiale che prende oggi il nome di Effetto Hall. Questo consiste
sostanzialmente nell’instaurarsi di una differenza di potenziale, detto potenziale di Hall VH , sulle facce
opposte di un campione metallico.
Nel seguente capitolo partiremo da un’analisi più precisa dell’effetto Hall classico fino ad arrivare alla
scoperta di un altro effetto detto effetto Hall quantistico.
1.1 Effetto Hall classico
L’effetto Hall si osserva in apparati sperimentali costituiti da un nastro sottile di materiale metallico
conduttore o semiconduttore, percorso da una corrente di intensità 𝐼 sottoposta all’azione di un campo
magnetico 𝑩.
Per descrivere il fenomeno supponiamo la corrente avente verso concorde all’asse x e supponiamo il campo
magnetico uniforme e diretto lungo l’asse z: sotto queste condizioni si manifesta una differenza di
potenziale trasverso, detto potenziale o tensione di Hall VH , tra le superfici laterali del conduttore.
Fig.1 Rappresentazione schematica dell’apparato descritto
A partire da tale tensione è possibile determinare la resistenza trasversa, detta resistenza di Hall che risulta
pari a:
𝑅𝐻 =
𝑉𝐻
𝐵
=
𝐼
𝑒 ∙ 𝑛𝑒
(1.1)
Dove con 𝑒 è indicata la carica dell’elettrone e con 𝑛𝑒 la densità dei portatori di carica.
Ciò che rende questo effetto importante è che dal verso della tensione VH è possibile determinare il segno
dei portatori di carica. Altro aspetto importante è che la resistenza trasversa RH, pur avendone le dimensioni,
non corrisponde però alla resistenza del materiale. Essa è inoltre indipendente dalla geometria del sistema e
risulta proporzionale all’intensità del campo magnetico 𝑩 applicato.
1.2 Il modello di Drude
Per descrivere il caso quantistico è importante definire prima alcune grandezze fondamentali quali resistività
e conducibilità longitudinali e di Hall.
6
Per farlo consideriamo un sistema elettronico bidimensionale: ciò che si osserva è che in assenza di un
campo magnetico la corrente indotta dal campo elettrico 𝑬 risulta parallela al campo stesso e la densità di
corrente risulta pari a 𝑱 = 𝜎𝑬 dove 𝜎 è la conducibilità del materiale.
In presenza di un campo magnetico 𝑩 si crea inoltre una densità di corrente trasversa che tende ad
accumulare le cariche sui bordi del campione fino al raggiungimento dell’equilibrio tra la forza elettrica
generata da questa distribuzione di carica e la forza di Lorentz generata dal campo magnetico. Nel caso
ideale solo la componente di 𝑩 perpendicolare al sistema 2-d influenza il moto elettronico mentre solo la
componente del campo elettrico che giace sul piano del sistema ha effetti sulla corrente.
In questo caso possiamo quindi scrivere la relazione tra la corrente e il campo E introducendo la densità di
corrente bidimensionale 𝐉 e il tensore conducibilità 𝝈:
𝑱 = 𝝈𝑬
(1.2)
Considerando il sistema 2-d giacente sul piano XY possiamo scrivere più esplicitamente dalla (1.2) :
𝐽𝑥 = 𝜎𝑥𝑥 𝐸𝑥 + 𝜎𝑥𝑦 𝐸𝑦
𝐽𝑦 = 𝜎𝑦𝑥 𝐸𝑥 + 𝜎𝑦𝑦 𝐸𝑦
(1.3)
Per l’isotropia del sistema 𝜎𝑥𝑥 = 𝜎𝑦𝑦 detta conducibilità longitudinale e 𝜎𝑥𝑦 = −𝜎𝑦𝑥 detta conducibilità di
Hall.
La conducibilità è però l’inverso nel senso matriciale del tensore resistività: 𝜎𝑖𝑗 = (𝜌−1 )𝑖𝑗 .
Quindi possiamo riscrivere la (1.2) come:
𝑬 = 𝝆𝑱
(1.4)
e le relazioni (1.3) in funzione del tensore resistività come:
𝐸𝑥 = 𝜌𝑥𝑥 𝐽𝑥 + 𝜌𝑥𝑦 𝐽𝑦
𝐸𝑦 = 𝜌𝑦𝑥 𝐽𝑥 + 𝜌𝑦𝑦 𝐽𝑦
(1.5)
Dove
𝜌𝐿 = 𝜌𝑥𝑥 = 𝜌𝑦𝑦 =
𝜎𝑥𝑥
2
+ 𝜎𝑥𝑦
2
𝜎𝑥𝑥
(1.6)
è detta resistività longitudinale, e
𝜌𝐻 = 𝜌𝑥𝑦 = −𝜌𝑦𝑥 = −
𝜎𝑥𝑦
2
𝜎𝑥𝑥
2
+ 𝜎𝑥𝑦
(1.7)
è detta resistività di Hall.
Una volta definite tali grandezze vediamo come sono legate alle caratteristiche del materiale.
Consideriamo una barretta di Hall soggetta all’azione di un campo elettrico 𝑬 e di un campo magnetico
𝑩 diretto lungo l’asse z.
7
Fig.2 Rappresentazione schematica del sistema in esame.
Sotto queste condizioni l’equazione del moto degli elettroni che si muovono nel piano con un momento
𝒑 = 𝑚𝑒 𝒗 = (𝑝𝑥 , 𝑝𝑦 ) soggetti all’azione dei campi è descritta dal Modello di Drude ed è data da:
𝑚𝑒
𝑑𝒗
𝒗×𝑩
𝒗
= −𝑒 (𝑬 +
) − 𝑚𝑒
𝑑𝑡
𝑐
𝜏
(1.8)
Dove con 𝜏 è indicato il tempo di rilassamento definito come il tempo medio tra un urto e il successivo.
L’ultimo termine indica infatti una forza viscosa proporzionale alla velocità che tiene conto delle impurità del
materiale e delle interazioni tra gli elettroni.
In condizioni di stazionarietà dove 𝑑𝑣 ⁄𝑑𝑡 = 0 possiamo esprimere la (1.8) con la seguente relazione:
𝒗+
𝑒𝜏
𝑒𝜏
(𝒗 × 𝑩) = −
𝑬
𝑚𝑒
𝑚𝑒
(1.9)
La densità di corrente è legata alla velocità dalla relazione:
𝑱 = − 𝑛𝑒 𝑒𝒗
Dove 𝑛𝑒 = 𝐿
𝑁
𝑥 𝐿𝑦
(1.10)
è la densità elettronica bidimensionale.
Usando la notazione matriciale possiamo riscrivere le relazioni precedente nel seguente modo:
1
𝑱(
−𝜔𝑐
𝑒 2 𝑛𝑒 𝜏
𝜔𝑐
)=
𝑬
1
𝑚𝑒
(1.11)
Dove con 𝜔𝑐 è indicata la frequenza di ciclotrone pari a 𝑒𝐵⁄𝑚𝑒 .
In assenza di campo magnetico è valida la relazione 𝑬 = 𝜌𝑱 dove la resistività è pari a:
𝜌=
𝑚𝑒
𝑛𝑒 𝑒 2 𝜏
(1.12)
Confrontando la (1.11) con le relazioni (1.5), troviamo:
𝜌𝐿 ≡ 𝜌𝑥𝑥 =
𝑚𝑒
𝑛𝑒 𝑒 2 𝜏
(1.13)
8
𝜌𝐻 ≡ 𝜌𝑥𝑦 =
𝐵
𝑛𝑒 𝑒𝑐
(1.14)
La resistività di Hall risulta quindi direttamente proporzionale all’intensità del campo magnetico in cui il
sistema è immerso e risulta indipendente dal tempo di rilassamento: questo significa quindi che non viene
influenzata dalle impurità del materiale responsabili degli scattering tra elettroni e reticolo del materiale.
1.2.1 Resistività e resistenza di Hall
Una proprietà molto importante e interessante riguarda la relazione tra la resistività e la resistenza trasversa
o di Hall.
Resistività e resistenza sono legate dalla seconda legge di Ohm 𝑅 = 𝜌𝐿/𝑆 dove L è la lunghezza del
conduttore e S la sua sezione, per cui differiscono per un fattore geometrico. Tuttavia nel caso della
resistenza trasversa RH si dimostra che le due coincidono.
Per dimostrarlo consideriamo un campione di un materiale di lunghezza 𝐿𝑦 lungo la direzione 𝑦, in cui si è
instaurata la tensione di Hall VH relativa alla corrente nella direzione x. La resistenza trasversa che si misura
è, ricordandoci della relazione (1.4), uguale a:
𝑅𝐻 =
𝑉𝐻 𝐿𝑦 𝐸𝑦 𝐸𝑦
=
=
= 𝜌𝐻
𝐼𝑥
𝐿𝑦 𝐽𝑥
𝐽𝑥
(1.15)
Quindi dalla (1.14) possiamo scrivere:
𝑅𝐻 ≡ 𝜌𝐻 =
𝐵
𝑛𝑒 𝑒𝑐
(1.16)
È importante notare che la resistenza di Hall è si indipendente dalla geometria del sistema ma risulta legata
al tipo di materiale dalla densità elettronica bidimensionale.
Resistenza e resistività longitudinali sono invece legate da un fattore adimensionale che tiene conto della
geometria del sistema per cui:
𝑅𝐿 ≡ 𝜌𝑥𝑥
𝐿𝑥 𝐿𝑥 𝑚𝑒
=
𝐿𝑦 𝐿𝑦 𝑛 𝑒 𝑒 2 𝜏
(1.17)
1.3 La scoperta dell’effetto Hall quantistico QHE
I fenomeni descritti nei paragrafi precedenti si osservano in presenza di campi magnetici deboli. In caso di
campi magnetici intensi e a basse temperature è necessario ricorrere alla meccanica quantistica.
Il QHE venne scoperto prima sperimentalmente e solo più tardi venne spiegata la teoria alla base del
fenomeno.
Le prime misure della conducibilità e della resistività in campioni soggetti a campi magnetici intensi furono
effettuate nel 1978 dai fisici Wakabayashi e Kawaji su un sistema Si MOS. Essi trovarono che in alcune
regioni la conducibilità longitudinale 𝜎𝑥𝑥 diveniva abbastanza piccola (~10−4 𝑚ℎ𝑜) mentre la conducibilità
di Hall 𝜎𝑥𝑦 seguiva un andamento pari a 𝑛𝑒 𝑒⁄𝐵 corrispondente all’inverso della (1.16).
9
Tuttavia il QHE fu scoperto qualche anno più tardi nel 1980 dal fisico Klaus von Klitzing, su un campione
preparato da Dorda e Pepper [1]. Per questa scoperta egli fu insignito del Premio Nobel per la fisica nel
1985. Effettuando delle misure più accurate della resistenza RH, variando la densità elettronica in un campo
magnetico fissato in regime di bassa temperatura, trovò che in alcune regioni dette plateaux la resistenza di
Hall presentava un andamento costante mentre la resistenza longitudinale si annullava. Più precisamente
trovò che la resistenza di Hall in tali regioni era esattamente uguale a:
𝑅𝐻 =
1
ℎ
= 2
𝜎𝐻 𝑛𝑒
(1.17)
Dove ℎ è la costante di Plank e 𝑛 un numero intero ∈ 𝑁 che viene determinato negli esperimenti con una
precisione altissima: circa una parte per miliardo.
In altre parole, ciò che si osservò fu che resistenza e conducibilità risultano dipendenti solo da costanti
fondamentali e non dalla geometria del sistema e che per determinati intervalli del campo magnetico
applicato queste sono quantizzate, da cui deriva il nome del fenomeno. La quantizzazione, manifestazione
dell’invarianza di gauge che vedremo nel seguente capitolo, ha l’effetto di azzerare la probabilità di urti
dissipativi tra i portatori di carica e il reticolo cristallino e quindi la resistenza longitudinale diviene nulla.
Fig. 3 Dalle due curve rappresentate possiamo notare la quantizzazione, riscontrabile nei plateux, della resistenza
trasversa RH e il corrispondente annullamento della resistenza longitudinale negli stessi intervalli del campo
magnetico corrispondenti agli intervalli in cui 𝑅𝐻 è costante.
Ognuno di questi plateaux è centrato su un valore del campo magnetico pari a:
𝐵=
𝑛𝑒 ℎ 𝑛𝑒
= 𝛷0
𝑛 𝑒
𝑛
(1.18)
Dove con 𝛷0 è indicato un quanto del flusso del campo magnetico.
[1] K. v Klitzing, G. Dorda, M. Pepper, “New Method for High-Accuracy Determination of the Fine-Structure Constant Based on
Quantized Hall Resistance”,1985, Phys. Rev. Lett. 45 494.
10
Capitolo 2
Sistemi elettronici bidimensionali
In questo capitolo verrà descritto il problema quantistico di un sistema elettronico bidimensionale in
presenza di un campo magnetico intenso. Verranno a tal proposito trascurate le interazioni elettroneelettrone e non sarà considerato il momento magnetico di spin associato all’elettrone. Tale scelta si spiega
col fatto che in presenza di un campo magnetico intenso si verifica l’effetto Zeeman: per elettroni liberi i
livelli energetici associati a diversi valori di spin subiscono una separazione (splitting) data da ∆= 𝑔𝜇𝐵 𝐵
dove 𝜇𝐵 è il magnetone di Bohr e 𝑔 il fattore di Landè. Tale effetto può essere trascurato in quanto, essendo
in presenza di campi magnetici intensi, gli effetti dovuti allo spin risultano trascurabili rispetto a quelli dovuti
al campo stesso.
Per scrivere l’equazione di Schrödinger di tale sistema è necessaria la scelta di una gauge: le più convenienti
sono la gauge di Landau e la gauge simmetrica. Descriveremo inoltre la quantizzazione dei livelli di Landau e
gli effetti delle impurità del materiale.
2.1 Moto elettronico in meccanica quantistica
2.1.1 Hamiltoniana per elettroni non interagenti
L’Hamiltoniana nel caso quantistico per elettroni liberi è data da:
𝐻=
1
[𝒑 − 𝑒𝑨(𝒓)]2 + 𝑔𝜇𝐵 𝒔𝑩
2𝑚𝑒
(2.1)
Dove 𝒑 è l’operatore momento (quantità di moto), 𝑨 è il potenziale vettore corrispondente al campo
magnetico (𝑟𝑜𝑡𝑨 = 𝑩), 𝑔 è il fattore di Landé che nel vuoto è ~2 ma in un semiconduttore può essere
minore, 𝜇𝐵 è il magnetone di Bohr e 𝑠 è il numero quantico di spin. Nella trattazione seguente il secondo
termine riguardante il momento di spin verrà trascurato, così come non verranno considerate le interazioni
elettrone-elettrone.
Il momento 𝒑 soddisfa le relazioni di commutazione [𝑝𝑖 , 𝑟𝑗 ] = (ħ⁄𝑖 )𝛿𝑖,𝑗 dove 𝑖, 𝑗 = 𝑥, 𝑦, 𝑧 e 𝛿𝑖,𝑗 è la delta di
Kronecker. Al contrario di ciò che avviene in meccanica classica questo operatore non è direttamente
proporzionale all’operatore velocità. Quest’ultimo infatti in meccanica quantistica deriva dall’equazione del
moto di Heisenberg:
𝑖
𝒑 − 𝑒𝑨
𝒗 = [𝐻, 𝒓] =
ħ
𝑚𝑒
(2.2)
Per ovviare questo problema si introduce l’operatore momento dinamico 𝝅, proporzionale all’operatore
velocità:
𝝅 = 𝑚𝑒 𝒗 = 𝒑 − 𝑒𝑨
Tale operatore segue inoltre la seguente relazione di commutazione:
(2.3)
11
[𝜋𝑥 , 𝜋𝑦 ] = [𝑝𝑥 − 𝑒𝐴𝑥 (𝑟), 𝑝𝑦 − 𝑒𝐴𝑦 (𝑟)] = 𝑒{[𝑝𝑥 , 𝐴𝑦 ] − [𝑝𝑦 , 𝐴𝑥 ]}
𝜕𝐴𝑦 𝜕𝐴𝑥
ħ2
= −𝑖𝑒ħ (
−
) = −𝑖𝑒ħ(∇ × 𝐴)𝑧 = −𝑖𝑒ħ𝐵 = −𝑖 2
𝜕𝑥
𝜕𝑦
𝑙
(2.4)
Dove abbiamo introdotto il raggio di Larmor 𝑙 = √ħ⁄|𝑒|𝐵 detto anche lunghezza magnetica: questa
lunghezza rappresenta una scala fondamentale del problema e in genere ricade in un intervallo di valori
compresi fra (50 − 100)Å . È importante notare inoltre che tale lunghezza risulta indipendente dalla
geometria e dalla composizione del materiale considerato. Per fare un esempio, considerando un campo
magnetico di 1 𝑇, la lunghezza magnetica risulta
≈ 2,5 × 10−8 𝑚.
Tornando all’operatore 𝝅 , anche questi, così come l’operatore 𝒑 non commuta con l’Hamiltoniana.
Consideriamo ora gli effetti del campo magnetico: supponendo quest’ultimo uniforme, il sistema deve
essere invariante per traslazione. Si introduce allora un altro operatore detto di traslazione, il quale deve
commutare con l’Hamiltoniana. Questi è dato da:
𝑲 = 𝒑 − 𝑒𝑨 + 𝑒𝑩 × 𝒓
(2.5)
ed è detto pseudomomento.
La relazione di commutazione degli operatori traslazione è data da:
[𝐾𝑥 , 𝐾𝑦 ] = −𝑖ħ𝑒𝐵 = 𝑖
ħ2
𝑙2
(2.6)
Questa non commutatività dell’operatore traslazione è espressione del fatto che un moto in un campo
magnetico induce una fase nella funzione d’onda detta di Aharonov-Bohm.
2.1.2 Gauge simmetrica
Per determinare la funzione d’onda del sistema è necessario procedere definendo la gauge da utilizzare. Per
un sistema sotto l’effetto di un campo magnetico si sceglie una gauge simmetrica.
L’Hamiltoniana infatti non dipende direttamente dal campo magnetico B applicato ma dal potenziale vettore
A, la cui scelta non è univoca: differenti scelte del potenziale vettore generano il medesimo campo
magnetico ma risultati diversi per la funzione d’onda.
Per una funzione reale e regolare 𝜒(𝑟), si definisce una trasformazione di gauge pari a:
𝑨′ (𝒓) = 𝑨(𝒓) + ∇𝜒(𝒓)
(2.7)
dove A(r) e A’(r) sono espressione dello stesso campo magnetico
Scrivendo l’Hamiltoniana come:
𝐻=
1
[𝒑 − 𝑒𝑨(𝒓)]2 + 𝐻𝑝𝑜𝑡
2𝑚𝑒
(2.8)
12
dove 𝐻𝑝𝑜𝑡 indica un generico potenziale esterno, è possibile definire l’autofunzione 𝛷(𝒓) corrispondente
all’autovalore 𝐸 dell’Hamiltoniana.
Allora autofunzioni dello stesso autovalore 𝐸 dell’Hamiltoniana in cui A è sostituito con A’ sono date da:
𝛷′ (𝒓) = 𝛷(𝒓) exp (
𝑖𝑒𝜒(𝒓)
)
ħ
(2.9)
Poiché χ(r) è una funzione reale, la scelta del gauge non influisce sulla probabilità |𝛷(𝒓)|2 di trovare
l’elettrone in r. Quest’invarianza di una osservabile rispetto alla libertà nella scelta del potenziale vettore è
definita invarianza di gauge.
2.2 Livelli di Landau
Per descrivere l’Hamiltoniana di un elettrone libero confinato a muoversi in un sistema bidimensionale
usiamo il momento dinamico 𝝅: esso infatti è un operatore invariante per trasformazioni di gauge del tipo
descritto nel paragrafo precedente.
Possiamo scrivere l’Hamiltoniana nel modo seguente:
𝐻=
1
𝝅2
2𝑚𝑒
(2.10)
Abbiamo visto che le componenti del momento dinamico non commutano tra loro dalla (2.4).
Si introduce quindi l’operatore posizione utilizzando gli operatori del centro delle coordinate (X,Y). Possiamo
definire tale operatore come:
𝒓 = (𝑋 +
𝑙2
𝑙2
𝜋𝑦 , 𝑌 − 𝜋𝑥 )
ħ
ħ
(2.11)
Questi operatori sono legati al pseudomomento 𝑲 dalle relazioni:
𝐾𝑥 = −𝑒𝐵𝑌 ; 𝐾𝑦 = 𝑒𝐵𝑋
(2.12)
E quindi commutano con il momento dinamico 𝝅 e il loro commutatore è pari a [𝑋, 𝑌] = 𝑖𝑙 2 .
Tornando all’Hamiltoniana possiamo quindi esprimerla in termini delle componenti del momento dinamico
come:
𝐻=
1
(𝜋 2 + 𝜋𝑦2 )
2𝑚𝑒 𝑥
(2.13)
Da questa relazione, poiché l’operatore momento dinamico appare in forma quadratica, possiamo notare
che l’Hamiltoniana ha la stessa struttura algebrica di quella riferita a un oscillatore armonico in una
13
dimensione. Introduciamo quindi gli operatori non hermitiani adimensionali abbassamento e innalzamento, i
quali soddisfano la relazione di commutazione data da [𝑎, 𝑎 † ] = 1 e sono dati da:
𝑎=
𝑎† =
𝑙
ħ√2
𝑙
ħ√2
(𝜋𝑥 − 𝑖𝜋𝑦 )
(2.14)
(𝜋𝑥 + 𝑖𝜋𝑦 )
(2.15)
Dove con 𝑙 è sempre indicata la lunghezza magnetica.
Possiamo quindi riscrivere l’Hamiltoniana come:
1
𝐻 = ħ𝜔𝑐 (𝑎† 𝑎 + )
2
(2.16)
Gli autostati dell’Hamiltoniana sono gli stessi dell’operatore numero 𝑎† 𝑎: 𝑎† 𝑎|𝑛⟩ = 𝑛|𝑛⟩, dove gli operatori
abbassamento e innalzamento agiscono nel seguente modo:
𝑎|𝑛⟩ = √𝑛|𝑛 − 1⟩
𝑎† |𝑛⟩ = √𝑛 + 1|𝑛 + 1⟩
(2.17)
(2.18)
Dove 𝑛 ∈ 𝑁. Lo stato |0⟩ è definito tale che 𝑎|0⟩ = 0.
I livelli energetici sono discretizzati come per l’oscillatore armonico in:
1
𝐸𝑛 = ħ𝜔𝑐 (𝑛 + )
2
(2.19)
Tali livelli discretizzati sono i cosiddetti livelli di Landau e sono indipendenti dalla gauge utilizzata.
Notiamo inoltre che in presenza del campo magnetico tali livelli sono equispaziati con un gap di energia
proporzionale al campo stesso.
2.2.1 Degenerazione dei livelli e autostati del sistema
A questo punto notiamo una discrepanza: partendo col considerare il moto di una particella in un piano,
avente quindi 2 gradi di libertà, siamo giunti però a un risultato che è quello di un oscillatore armonico in
una dimensione. Questo si spiega col fatto che non abbiamo considerato la degenerazione dei livelli
energetici: al contrario di ciò che avviene per l’oscillatore armonico infatti, nel sistema da noi considerato
per ogni livello di Landau non abbiamo un unico stato ad esso associato. Per definire la degenerazione dei
livelli partiamo col considerare la gauge simmetrica 𝑨 = (−𝐵𝑦 ⁄2 , 𝐵𝑥 ⁄2 , 0): questa scelta del gauge
permette al sistema di godere dell’invarianza e implica nuove vantaggiose relazioni di commutazione per gli
operatori.
14
A seguito della scelta del gauge possiamo esprimere il momento angolare del sistema come:
𝐿𝑧 = −
ħ
𝑙2 2
2
2)
(𝑋
+
𝑌
+
(𝜋 + 𝜋𝑦2 )
2𝑙 2
2ħ 𝑥
(2.20)
Poiché [𝐿𝑧 , 𝐻] = 0, l’autovalore del momento angolare può essere usato per distinguere stati relativi allo
stesso livello energetico.
È necessario a questo punto introdurre dei nuovi operatori di scala 𝑏, 𝑏 † che rispettino le seguenti relazioni
di commutazione:
[𝑏, 𝑏 † ] = 1,
[𝑏, 𝑎] = [𝑏 † , 𝑎] = 0,
[𝑏, 𝐻] = [𝑏 † , 𝐻] = 0
Tali operatori sono definiti da:
𝑏=
𝑏† =
1
𝑙√2
1
(𝑋 + 𝑖𝑌)
(2.21)
(𝑋 − 𝑖𝑌)
(2.22)
𝑙√2
È possibile anche in questo caso introdurre l’operatore numero 𝑏 † 𝑏: 𝑏 † 𝑏|𝑚⟩ = 𝑚|𝑚⟩ da cui otteniamo il
nuovo numero quantico 𝑚 che vedremo agisce sulla forma analitica della funzione d’onda lasciandone però
immutato lo spettro energetico.
Una volta definiti tali operatori possiamo scrivere il momento angolare come:
𝐿𝑧 = ħ(𝑎† 𝑎 − 𝑏 † 𝑏)
(2.23)
E quindi l’autovalore del momento angolare sarà dato da ħ(𝑛 − 𝑚).
Risulta evidente come i livelli di Landau siano degeneri: in un sistema 2-d come quello da noi descritto infatti
la particella presenta 2 gradi di liberta associati ai diversi numeri quantici 𝑛, 𝑚. Ma poiché l’Hamiltoniana
risulta dipendente dal solo numero quantico 𝑛, questo implica che tutti gli stati con 𝑛 fissato e numero
quantico 𝑚 diverso hanno la stessa energia e sono pertanto degeneri.
Nella gauge simmetrica ogni livello di Landau contiene orbitali degeneri dati dal numero quantico 𝑚. Ciò che
rimane uguale per ogni livello è la degenerazione per unità di superficie data da:
𝑛𝐵 =
1
2𝜋𝑙 2
(2.24)
Per poter adesso scrivere le funzioni d’onda relative agli autostati del sistema riprendiamo il concetto per
cui, nella gauge simmetrica, lo stato di un elettrone è descritto da un ket |𝑛, 𝑚⟩ dove 𝑛, 𝑚 ≥ 0 sono i numeri
quantici principali del sistema. Tale autostato è simultaneamente stato degli operatori 𝑎, 𝑎† , 𝑏 e 𝑏 † :
15
𝑎 † 𝑎|𝑛, 𝑚⟩ = 𝑛|𝑛, 𝑚⟩; 𝑏 † 𝑏|𝑛, 𝑚⟩ = 𝑚|𝑛, 𝑚⟩. Per ottenere le funzioni d’onda espresse in funzione delle
coordinate 𝒓 del sistema devo prima esprimere gli operatori di scala in funzione di queste ultime come:
𝑎=
𝑏=
1
𝑖
𝜕
𝜕
[− (𝑥 − 𝑖𝑦) − 𝑖𝑙 2 ( − 𝑖 )]
𝜕𝑥
𝜕𝑦
𝑙√2 2
1
𝑖
𝜕
𝜕
[ (𝑥 + 𝑖𝑦) + 𝑙 2 ( + 𝑖 )]
𝜕𝑥
𝜕𝑦
𝑙√2 2
(2.25)
(2.26)
Assumendo il campo magnetico B lungo la direzione opposta, è possibile introdurre le coordinate complesse
𝑧 = (𝑥 − 𝑖𝑦)/𝑙 e 𝑧 ∗ = (𝑥 + 𝑖𝑦)/𝑙. Possiamo a questo punto riscrivere gli operatori di scala in funzione di
queste coordinate come:
𝑎 = −𝑖√2 𝑒𝑥𝑝 (−
|𝑧|2 𝜕
|𝑧|2
) ∗ 𝑒𝑥𝑝 (
)
4 𝜕𝑧
4
(2.27)
𝑎† =
𝑖
√2
𝑒𝑥𝑝 (−
|𝑧|2
|𝑧|2
𝜕
) [𝑧 ∗ − 2 ] 𝑒𝑥𝑝 (
)
4
𝜕𝑧
4
E per gli altri operatori:
𝑏 = √2 𝑒𝑥𝑝 (−
|𝑧|2 𝜕
|𝑧|2
𝑒𝑥𝑝
)
(
)
4 𝜕𝑧
4
(2.28)
|𝑧|2
|𝑧|2
𝜕
𝑏 =
𝑒𝑥𝑝 (−
) [𝑧 − 2 ∗ ] 𝑒𝑥𝑝 (
)
4
𝜕𝑧
4
√2
†
1
La funzione d’onda dello stato fondamentale |0,0⟩ è ottenuto a partire dalle condizioni 𝑎|0,0⟩ = 𝑏|0,0⟩ = 0.
Posto ⟨𝒓|0,0⟩ ≡ 𝛹0,0 (𝒓) possiamo allora scrivere:
𝛹0,0 (𝒓) =
|𝑧|2
1
𝑟2
𝑒𝑥𝑝 (−
𝑒𝑥𝑝 (− 2 )
)=
4
4𝑙
𝑙√2𝜋
𝑙√2𝜋
1
(2.29)
Le funzioni d’onda degli stati successivi sono ottenuti a partire dallo stato fondamentale sfruttando gli
operatori innalzamento:
𝑛
𝛹𝑛,𝑚 (𝒓) =
𝑚
𝑎† 𝑏 †
√𝑛! √𝑚!
𝜑0,0 (𝒓)
(2.30)
16
Molto importante è la funzione d’onda corrispondente al livello energetico più basso, dove 𝑛 = 0:
𝛹0,𝑚 (𝒓) =
=
1
𝑙√2𝜋2𝑚 𝑚!
𝑧 𝑚 𝑒𝑥𝑝 (−
|𝑧|2
)=
4
𝑥 − 𝑖𝑦 𝑚
𝑟2
(
) 𝑒𝑥𝑝 (− 2 )
𝑙
4𝑙
𝑙√2𝜋2𝑚 𝑚!
1
(2.31)
Tale funzione d’onda rappresenta un elettrone localizzato circolarmente per cui il massimo della densità di
2
probabilità di trovare l’elettrone, data da |𝛹0,𝑚 (𝒓)| , giace lungo una circonferenza di raggio 𝑙√2𝑚 come
mostrato nella seguente figura.
2
|𝛹0,𝑚 (𝒓)|
𝑦
𝑥
2
Fig.4 Rappresentazione della distribuzione di probabilità |𝛹0,𝑚 (𝒓)| .
Il valore di aspettazione di 𝑟 2 è invece dato da ⟨0, 𝑚|𝑟 2 |0, 𝑚⟩ = 2(𝑚 + 1)𝑙 2 . Lo stato |0, 𝑚⟩ va considerato
come combinazione lineare di più orbite ciclotroniche di raggio 𝑙 aventi centro in un’orbita circolare di raggio
𝑙√2𝑚.
2.3 Condizione di quantizzazione e fase di Aharonov-Bohm
Abbiamo visto che lo stato corrispondente al più basso livello energetico è localizzato circolarmente; ciò che
è importante osservare è come cambia la fase della funzione d’onda lungo tale circonferenza.
La fase cambia di −2𝜋𝑚: questa è la condizione di quantizzazione del momento angolare.
L’effetto può essere visto come risultato dell’invarianza di gauge per il potenziale vettore 𝑨: ciò implica
infatti che una particella carica (ad esempio l’elettrone), che viaggia lungo una curva chiusa in presenza di un
campo magnetico debba assumere una fase:
𝑒
𝑒
𝑒
𝜑 = ∮ 𝑨 ∙ 𝑑𝒔 = ∫ 𝐵𝑛 ∙ 𝑑𝑆 = 𝜱
ħ
ħ
ħ
(2.32)
17
Data dal teorema di Stokes e dalla relazione 𝑟𝑜𝑡𝑨 = 𝑩.
Possiamo notare quindi come la differenza di fase ∆𝜑 fra qualunque coppia di traiettorie aventi lo stesso
punto finale, sia determinata dal flusso magnetico 𝜱 che attraversa la superficie racchiusa dalla traiettoria
delle particelle.
Tale fase, detta di Aharonov-Bohm risulta quindi dipendente solo dal flusso totale racchiuso dalla traiettoria
e non dal campo magnetico che l’attraversa. Poiché tale fase è definita come il cambiamento di fase dovuto
al momento angolare, possiamo dire che a uno stato con un momento angolare finito deve essere associato
un corrispondente flusso magnetico.
2.4 Moto in un campo elettrico esterno e gauge di Landau
Partiamo col considerare un sistema elettronico bidimensionale sottoposto all’azione di un campo elettrico
esterno 𝑬 diretto lungo l’asse x. In questo caso il momento angolare non viene conservato e la gauge
simmetrica non è più una scelta conveniente: si introduce quindi la gauge di Landau. Per il potenziale vettore
questa si traduce in:
𝑨 = (0, 𝐵𝑥 , 0)
(2.33)
Possiamo quindi scrivere l’Hamiltoniana come:
𝐻=
1
2
[𝑝2 + (𝑝𝑦 − 𝑒𝐵𝑥 ) ] − 𝑒𝐸𝑥
2𝑚𝑒 𝑥
(2.34)
Con la scelta di questa gauge il momento 𝒑 viene conservato lungo l’asse delle ordinate, questo ci permette
di scrivere la funzione d’onda nel modo seguente:
𝛹(𝒓) =
1
√𝐿𝑦
exp(𝑖𝑘𝑦 𝑦) 𝛹(𝑥)
(2.35)
Dove 𝐿𝑦 ricordiamo essere la dimensione del campione lungo la direzione y.
Dalla relazione precedente possiamo quindi scrivere l’equazione di Schrödinger:
{
1
2
[𝑝2 + (ħ𝑘𝑦 − 𝑒𝐵𝑥 ) ] − 𝑒𝐸𝑥 } 𝛹(𝑥) = 𝛴𝛹(𝑥)
2𝑚𝑒 𝑥
(2.36)
Qui con 𝛴 è indicato l’autovalore dell’energia associata all’autostato 𝛹(𝑥).
Per una comodità nella notazione introduciamo il centro del potenziale:
𝑋 = −𝑘𝑦 𝑙 2 +
𝑒𝐸𝑚𝑒 𝑙 4
ħ2
(2.37)
18
In modo da poter riscrivere la (2.36) come:
(
1 2 𝑚𝑒 𝜔𝑐2
𝑚𝑒 𝐸 2
(𝑥 − 𝑋)2 ) 𝛹(𝑥) = [𝛴 + 𝑒𝐸𝑋 −
𝑝𝑥 +
( ) ] 𝛹(𝑥)
2𝑚𝑒
2
2 𝐵
(2.38)
Anche in questo caso l’equazione di Schrödinger risulta essere quella di un oscillatore armonico il cui
potenziale è appunto centrato in X.
È possibile scrivere le autofunzioni del sistema nel modo seguente:
1
1
1 4
1 2
(𝑥 − 𝑋)2
𝑥−𝑋
𝛹(𝑥) = ( ) ( 𝑛 ) 𝑒𝑥𝑝 (−
)
) 𝐻𝑛 (
2
𝜋
2 𝑛! 𝑙
2𝑙
𝑙
(2.39)
Dove con 𝐻𝑛 sono indicati i polinomi di Hermite dati dalla relazione:
𝐻𝑛 (𝑥) =
(−1)𝑛
exp(𝑥
2)
𝑑𝑛
𝑒𝑥𝑝(−𝑥 2 )
𝑑𝑥 𝑛
(2.40)
L’autovalore dell’energia è invece dato da:
1
𝑚𝑒 𝐸 2
𝛴 = ħ𝜔𝑐 (𝑛 + ) − 𝑒𝐸𝑋 +
( )
2
2 𝐵
(2.41)
Il primo termine corrisponde all’autovalore dell’energia di un oscillatore armonico, il secondo termine è
l’energia potenziale dovuta alla presenza del campo e l’ultimo termine è l’energia cinetica dovuta al moto
traslazionale.
Il valor medio (di aspettazione) dell’operatore velocità lungo le 2 direzioni principali è dato da:
⟨𝛹|𝑣𝑥 |𝛹⟩ = ⟨𝛹|
⟨𝛹|𝑣𝑦 |𝛹⟩ = ⟨𝛹|
𝑝𝑥
|𝛹⟩ = 0
𝑚𝑒
1
𝑒𝐵
𝐸
𝐸
(𝑋 − 𝑥) − |𝛹⟩ = −
(𝑝𝑦 − 𝑒𝐵𝑥)|𝛹⟩ = ⟨𝛹|
𝑚𝑒
𝑚𝑒
𝐵
𝐵
(2.42)
(2.43)
Il moto elettronico avviene lungo la perpendicolare al campo elettrico con una velocità 𝐸 ⁄𝐵 proprio come in
meccanica classica: la funzione d’onda si estende lungo tale linea equipotenziale e la sua larghezza è
dell’ordine di 𝑙√2𝑛 + 1.
19
2.5 Effetti delle impurità
Finora abbiamo considerato sempre il caso di un campione puro e quindi ideale. Nello studio dell’IQHE ci si
scontra invece col problema delle impurità del materiale del campione considerato. Le impurità, essendo
sostanzialmente atomi, molecole o ioni di un elemento diverso rispetto a quelli del campione, generano
delle interazioni tra gli elettroni e il reticolo cristallino. Questo fenomeno avviene ovviamente a causa del
diverso potenziale delle impurità che va quindi sommato agli altri termini dell’Hamiltoniana.
Per studiare gli effetti delle impurità si parte in genere col considerare il libero cammino medio 𝜆 e il tempo
di rilassamento 𝜏, definiti come la distanza e il tempo medio tra un urto e il successivo. Supporremo di
seguito che gli urti tra gli elettroni e il reticolo siano perfettamente elastici.
La prima correzione riguarda gli autovalori dell’energia considerati nei paragrafi precedenti: gli effetti delle
impurità infatti possono essere considerati sommando all’autovalore dell’oscillatore armonico un termine
complesso pari a:
1
ħ
𝐸𝑛 = ħ𝜔𝑐 (𝑛 + ) + 𝑖
2
𝜏
(2.44)
In questo modo ogni livello di Landau viene suddiviso in un set di livelli energetici caratterizzati da una
densità di tipo Lorentziano.
Fig. 5 Splittamento dei livelli di Landau per diversi valori del campo 𝐵 e del tempo 𝜏.
Si tratta tuttavia di un’approssimazione: la distribuzione Lorentziana risulta utile per valori sufficientemente
piccoli di 𝜔𝑐 𝜏 ma fallisce per valori dell’intensità del campo magnetico elevati.
Abbiamo visto come il moto degli elettroni segua una traiettoria ciclotronica. Ma cosa succede in presenza
delle impurità? Se queste sono presenti in quantità ridotte e sono sufficientemente distanziate in confronto
al raggio della traiettoria, allora quello che succede è che un certo numero di elettroni continuerà nel suo
moto senza cambiamenti dell’energia al contrario di quelli sottoposti al potenziale delle impurità. La
variazione dell’energia degli autostati sarà uguale a ±𝑛ħ𝜔𝑐 a seconda del fatto che il potenziale sia repulsivo
o attrattivo.
20
Per alcuni elettroni quindi non ci sono mutamenti nel moto, tranne per il fatto che il raggio ciclotronico è
sostituito dalla lunghezza magnetica 𝑙.
Altri effetti riguardano la corrente elettrica: a basse temperature, utilizzate in genere per lo studio dell’IQHE,
gli elettroni popolano tutti gli stati di energie inferiore all’energia di Fermi (che dipende da temperatura e
densità elettronica). A causa delle impurità però l’elettrone può trovarsi in uno stato localizzato o in uno
stato esteso; a basse temperature solo gli stati estesi partecipano alla conduzione elettrica. Questi stati si
organizzano nel materiale con una struttura a bande come mostrato in figura:
Fig.6 Distribuzione degli stati localizzati e estesi in funzione dell’energia.
Ciò che si osserva è che la presenza delle impurità riduce il numero di stati estesi convertendoli in stati
localizzati: quindi il numero di stati in cui avviene la conduzione si riduce.
La densità degli stati estesi e i plateux presenti nell’andamento della resistenza di Hall sono strettamente
correlati tra loro dal campo magnetico. Sappiamo infatti che in assenza di un campo magnetico, la densità
degli stati è una funzione costante dell’energia. La presenza del campo genera invece una separazione dei
livelli data dall’energia ciclotronica: in questo modo vengono creati stati proibiti tra un livello di Landau e
l’altro. Al crescere dell’intensità del campo aumenta la separazione tra i livelli, il cui valore dell’energia si
avvicina fino a superare quello dell’energia di Fermi: in questo modo, all’aumento dell’intensità del campo
corrisponde una diminuzione del numero di stati estesi completamente pieni al di sotto dell’energia di
Fermi. Superato questo valore gli stati non partecipano più alla conduzione. Quando il livello dell’energia di
Fermi ricade tra due livelli di Landau, gli elettroni non possono saltare al livello successivo: è in queste
condizioni che la resistenza longitudinale diviene nulla e la resistenza trasversa 𝑅𝐻 rimane costante
formando i plateaux.
21
Fig.7 Rappresentazione schematica del fenomeno descritto: la resistenza trasversa rimane costante per tutto il tempo
in cui l’energia di Fermi ricade tra due livelli, casi (a) e (b), e cambia quando l’energia di Fermi ricade all’interno di un
livello, caso (c). in questo caso stiamo assumendo che il livello di Fermi sia fisso e che vari solo l’intensità del campo.
Nel Capitolo 1 abbiamo cisto che la resistenza di Hall nel caso classico è data semplicemente da 𝐵⁄𝑒𝑛𝑒
mentre il numero di stati che partecipano alla conduzione per livello di Landau sono pari a 𝑒𝐵⁄ℎ. Quindi se
sono presenti ”𝑖" livelli di Landau completamente pieni al di sotto dell’energia di Fermi, che partecipano alla
conduzione, avrò una resistenza trasversa che sarà esattamente pari a ℎ⁄𝑖𝑒 2 .
Fig.8 Correlazione tra la separazione dei livelli energetici e l’andamento della resistenza trasversa e longitudinale al
variare dell’intensità del campo magnetico.
Tornando alle impurità, al contrario di quello che uno si aspetterebbe, la loro presenza è indispensabile per
osservare la quantizzazione intera e quindi i plateau. Infatti si osserva che aumentando, entro limiti
ragionevoli, la quantità di disordine, i plateau diventano più evidenti. Se si considera invece un campione
privo di impurità questi spariscono completamente.
22
Capitolo 3
L’effetto Hall quantistico QHE
Dopo aver affrontato la teoria alla base dell’effetto Hall quantistico, in questo capitolo vedremo come
questo effetto viene sfruttato in alcuni apparecchi elettronici.
Partiremo con la descrizione dell’apparato sperimentale utilizzato nell’esperimento con cui si scoprì l’IQHE e
descriveremo poi sistemi utilizzati oggigiorno. Affronteremo poi il problema degli effetti della temperatura
sulla conducibilità e sulla resistività in tali sistemi e in ultimo analizzeremo gli effetti dovuti alla finitezza del
campione: i cosiddetti effetti di bordo.
3.1 Realizzazione di sistemi elettronici bidimensionali
L’IQHE è stato scoperto in un sistema Si MOSFET , il cui acronimo sta per “metal-oxide-semiconductor fieldeffect transistor”. In questo sistema gli elettroni sono intrappolati nella "banda di inversione" tra lo strato di
materiale isolante e il semiconduttore, la cui larghezza è di circa 30 Å.
L’eterogiunzione GaAs-GaAlAs è un sistema elettronico bidimensionale più recente che venne utilizzato nella
scoperta dell’effetto Hall quantistico frazionario: l'FQHE. Quest’ultimo sistema è molto utilizzato negli
apparati odierni.
In comune questi sistemi hanno la densità elettronica e le dimensione del campione.
3.1.1 Primi esperimenti: Si MOS
Il primo sistema elettronico bidimensionale fu realizzato negli anni ’60 in un transistor MOS a effetto campo
al silicio. L’acronimo MOS deriva dai tre componenti della struttura: metal (metallo), oxide (ossido) e
semiconductor (semiconduttore).
Fig.9 Rappresentazione schematica di un sistema Si MOS.
Il sistema è realizzato combinando Si, un semiconduttore tridimensionale, un isolante dato dall’ossido del
silicio SiO2, e un metallo.
23
Di estrema importanza è il ruolo svolto dallo strato del semiconduttore. Il silicio è un elemento tetravalente,
ovvero in grado di accettare o cedere 4 elettroni, e ha una struttura cristallina molto simile a quella del
diamante (carbonio) formata quindi da legami di tipo covalente. Analizziamone ora il funzionamento.
Sappiamo che in un cristallo (semiconduttore) perfetto la banda di valenza è completamente piena mentre
la banda di conduzione è lasciata vuota. Per il silicio l’energia della banda proibita, il gap, tra le due bande è
di 1,17 eV: a temperatura ambiente il gap è molto più largo rispetto all’energia termica 𝑘𝐵 𝑇, dove
𝑘𝐵 = 1,38065 × 10−23 𝐽⁄𝐾 è la costante di Boltzmann, per cui il materiale si comporta come un isolante.
Lavorando a temperature più basse e drogando il silicio, questo acquista le proprietà di un conduttore.
Possiamo drogare il materiale con donori (drogaggio di tipo n), impurità pentavalenti come il fosforo P o
l’arsenico As, o con accettori (drogaggio di tipo p), impurità trivalenti come il boro B o l’indio In.
Un sistema Si MOSFET è realizzato con Si drogato p, quindi con accettori. Vediamo quindi cosa succede in
questo caso. Consideriamo un accettore: per completare i legami l’atomo trivalente necessita di un
elettrone: questi viene prelevato dalla banda di valenza BV e l’atomo si carica così negativamente.
L’elettrone catturato lascia nella BV un “buco” detto lacuna che interagisce con l’accettore avente carica
negativa, creando così uno stato legato. L’espressione dell’energia di legame tra l’elettrone e l’atomo
accettore può essere espressa come nel caso dell’elettrone nell’atomo di idrogeno (modello idrogenoide),
con la correzione della massa che in questo caso è data dalla massa efficace e dove l’energia di Coulomb è
espressa dalla costante dielettrica del semiconduttore. L’energia di legame ha la seguente forma:
𝐸𝑎 =
𝑒 4 𝑚∗
2(4𝜋𝜖ħ)2
(3.1)
Dove 𝑚∗ è la massa efficace dell’elettrone nel Si e 𝜀 ≅ 11,7 𝜀0 è la costante dielettrica del materiale. Lo
stato legato di energia inferiore giace al di sopra della BV di 𝐸𝑎 , dove abbiamo così indicato l’energia di
legame nel caso di un accettore.
Come mostrato in figura 3.1 al sistema è applicata una tensione 𝑉𝐺 tra il metallo e il semiconduttore. Per
vedere come si comportano gli elettroni in questo sistema, supponiamo che la temperatura coincida con lo
zero assoluto: l’energia di fermi 𝐸𝐹 del semiconduttore Si drogato p, giace appena sopra lo stato legato (3.1)
di energia inferiore. Possiamo distinguere tre casi:
a) Se 𝑉𝐺 = 0 allora l’energia di Fermi del metallo coincide con quella dello strato semiconduttore.
b) Se 𝑉𝐺 > 0 e il potenziale del metallo e più alta di quello del semiconduttore, allora il sistema si
comporta come un condensatore. Infatti tra il metallo e l’isolante, che ricordiamo essere l’ossido
SiO2, si instaura una carica positiva, mentre nell’interfaccia tra quest’ultimo e il semiconduttore si
instaura una carica negativa. Se 𝑉𝐺 è debole allora la carica negativa è data dagli accettori vicini
all’interfaccia che hanno acquisito una carica negativa. Questi sono confinati in una zona detta
“strato di esaurimento”: a causa del campo elettrico perpendicolare allo strato, generato da 𝑉𝐺 , i
livelli energetici si flettono verso l’interfaccia.
c) Se 𝑉𝐺 ≫ 0 allora la flessione dei livelli energetici aumenta: questo provoca uno spostamento della
banda di conduzione. Questa infatti viene a sovrapporsi con il livello di Fermi. Allora, vicino
all’interfaccia, gli elettroni vanno ad occupare quei livelli della BC che sono al di sotto dell’energia di
Fermi: questi sono confinati in uno strato bidimensionale lungo l’interfaccia in cui sono liberi di
muoversi. Questa zona è detta “zone di inversione” ed è fondamentale per osservare l’IQHE.
24
Fig.10 Rappresentazione dei livelli energetici in un campione di Si MOSFET. Le sferette nere rappresentano gli
accettori carichi negativamente e quelle bianche gli accettori privi di un elettrone. Non sono rappresentate le
bande dello strato isolante in quanto avente un gap molto elevato e poiché la sommità della BV ricade molto al di
sotto delle energie rappresentate.
Lo spessore della zone di esaurimento è di pochi micron, mentre lo strato di inversione è dell’ordine dei
10 nanometri. Per questo possiamo considerare in tale zona il campo elettrico uniforme e il potenziale
come lineare, mentre nello strato isolante il potenziale risulta infinito: ecco perché il moto elettronico
risulta confinato in uno strato bidimensionale.
Cambiando la tensione applicata 𝑉𝐺 è possibile modificare la densità elettronica del sistema: poiché la
conduttività è direttamente proporzionale a tale densità (vedi la relazione (1.14)) , il sistema può essere
utilizzato come transistor. In questi sistemi la densità utilizzata è di circa 1015 − 1017 𝑚−2 : a densità
inferiori l’effetto delle impurità diventa troppo forte. L’inconveniente in questi sistemi è dato dalla zona
di esaurimento che, essendo formata da accettori di carica negativa, si comporta come una sorgente di
potenziale di dispersione.
3.1.2 L’eterogiunzione 𝑮𝒂𝑨𝒔 − 𝑨𝒍𝑮𝒂𝑨𝒔
Attualmente, un sistema elettronico bidimensionale molto usato, è l’eterogiunzione
𝐺𝑎𝐴𝑠 − 𝐴𝑙𝐺𝑎𝐴𝑠. Questo sistema sfrutta le proprietà del gallio 𝐺𝑎 e dell’arsenico 𝐴𝑠, trivalenti e
dell’alluminio 𝐴𝑙, pentavalente. Il composto 𝐺𝑎𝐴𝑠 è in media tetravalente e forma un struttura
cristallina come il diamante in cui ogni atomo di gallio è legato a 4 atomi di arsenico e viceversa. Questi è
anche un isolante, con il livello dell’energia di Fermi tra la banda di valenza e la banda di conduzione. Il
composto 𝐴𝑙𝑥 𝐺𝑎1−𝑥 𝐴𝑠𝑥 ,in cui una parte del gallio è sostituita dall’alluminio, ha una struttura cristallina
simile ma un gap energetico più ampio: è quindi ancora più isolante.
Questi cristalli vengono formati con una tecnica chiamata “Epitassia da fasci molecolari” in cui la
struttura viene creato strato per strato: in questo modo è possibile controllare la composizione e
sostituire parte del gallio con l’alluminio. In questo modo viene formata l’eterogiunzione data dai due
sub-strati aventi gap diversi.
Supponiamo di lavorare anche in questo caso a una temperatura pari allo zero assoluto e di introdurre
nel sistema dei donori. Ciò che si osserva è che il livello di Fermi del substrato 𝐴𝑙𝑥 𝐺𝑎1−𝑥 𝐴𝑠𝑥 , giace
appena sopra il primo stato legato dei donori (la cui espressione è uguale alla relazione (3.1) in cui la
massa efficace è sostituita con quella dell’elettrone della banda di conduzione) che si trova più in alto
rispetto al fondo della banda di conduzione del substrato 𝐺𝑎𝐴𝑠.
25
Fig.11 Rappresentazione dei livelli energetici in un’eterogiunzione 𝐺𝑎𝐴𝑠 − 𝐴𝑙𝐺𝑎𝐴𝑠: la figura a sinistra in
assenza di donori, a destra in presenza di donori.
In questo sistema gli elettroni legati ai donori, si spostano nella banda di conduzione del substrato 𝐺𝑎𝐴𝑠. La
differente carica dei due substrati provoca una polarizzazione elettrica: infatti il substrato 𝐺𝑎𝐴𝑠 è caricato
negativamente e 𝐴𝑙𝑥 𝐺𝑎1−𝑥 𝐴𝑠𝑥 positivamente; il processo si interrompe quando una certa quantità di
elettroni si è spostata.
Uno dei vantaggi di questa struttura rispetto al sistema Si MOS è che il potenziale di dispersione risulta
molto più debole: inserendo gli elementi pentavalenti lontano dall’interfaccia, l’effetto può essere
ulteriormente ridotto. Questo permette di avere un campione ad alta mobilità. Applicando un campo
elettrico perpendicolare alla struttura è possibile controllare la densità elettronica, i cui valori utili sono simili
a quelli utilizzati in un sistema Si MOSFET.
3.2 Precisione nelle tecniche di misura
I risultati ottenuti da von Klitzing, Dorda e Pepper nel 1980 scatenarono subito l’interesse della comunità
metrologica internazionale. Questi infatti aprirono spazio alla possibilità di considerare l’effetto Hall
quantistico intero come metro di misura standard di resistenza, in quanto quest’ultima risulta dipendente
solo da costanti fondamentali ed è inoltre determinata con una precisione elevata. Il valore ufficiale di
questa resistenza standard, ottenuto per 𝑖 = 1, è:
𝑅𝐻 =
ℎ
= 25′ 812,807 𝛺
𝑒2
Questa è detta anche costante di von Klitzing.
3.3 Effetti di bordo
La dimensione finita dei dispositivi elettronici usati ha delle conseguenze sia sul moto elettronico, sia sulla
corrente che circola nel campione.
26
3.3.1 Moto elettronico ai bordi del campione
Per descrivere il moto degli elettroni ai bordi del campione, si considera il bordo stesso come un potenziale
di confinamento: quest’ultimo ovviamente influisce sullo stato degli elettroni del sistema.
Supponiamo il sistema avente forma rettangolare in cui il lato maggiore giace lungo l’asse y; ipotizziamo
inoltre che il potenziale di confinamento sia:
𝑉(𝑥) = {
0
𝑝𝑒𝑟 𝑥 < 𝑥0
> 0 𝑝𝑒𝑟 𝑥 > 𝑥0
(3.2)
In questa situazione è utile descrivere il sistema con la gauge di Landau per cui 𝐴 = (0, 𝐵𝑥 , 0). Il momento
angolare lungo la direzione y è quindi conservato e la funzione d’onda è un’onda piana.
Possiamo distinguere più casi a seconda della rapidità con cui varia il potenziale:
a) Se 𝑉(𝑥) varia lentamente con continuità, possiamo usare la funzione d’onda descritta dalla relazione
(2.39). Il campo elettrico è dato dal gradiente del potenziale: possiamo sviluppare in serie di Taylor
la funzione 𝑉(𝑥) e poiché questa varia lentamente, la derivata seconda e quelle di ordine superiore
possono essere trascurate entro il limite 𝛿𝑥 = 𝑙 √2𝑛 + 1. L’energia dell’elettrone è quindi data dalla
relazione (2.41).
b) Se 𝑉(𝑥) varia poco più rapidamente, non possiamo più trascurare i termini della serie di Taylor di
ordine superiore al primo. Se la funzione 𝑉(𝑥) è quadratica allora basta approssimare la serie al
secondo ordine: in questo caso quindi il sistema si riduce a quello di un oscillatore armonico e siamo
in grado di risolvere analiticamente l’equazione di Schrödinger.
c) Se 𝑉(𝑥) varia molto rapidamente, non è più possibile risolvere il sistema analiticamente: si ricorre
quindi a metodi numerici. I risultati di questi metodi mostrano che l’energia di uno stato elettronico
aumenta man mano che ci si avvicina al bordo del campione e che, in tale stato, un elettrone si
muove parallelamente al bordo stesso. Il moto dell’elettrone può essere compreso in meccanica
classica se lo si considera come una riflessione al bordo dell’orbita ciclotronica: l’orbita viene
“spezzata” al contatto con la barriera di potenziale del bordo, generando un’urto che consideriamo
elastico (Smrĉka 1984).
Fig.12 A sinistra è rappresentato il moto elettronico descritto al punto c); a destra è mostrata la dipendenza lungo la
direzione x dei livelli di Landau lungo la sezione A-B del campione.
3.3.2 Distribuzione della corrente ai bordi del sistema
Rifacendoci al punto c) del paragrafo precedente potremmo pensare che il moto elettronico e quindi la
corrente sia vincolata ai bordi del campione. Ma se fosse davvero così, allora avremmo che la velocità degli
27
elettroni sarebbe 2 ordini di grandezza superiore della velocità del suono nel materiale considerato,
ipotizzando una corrente 𝐼 = 10 𝜇𝐴 [2]. È importante notare inoltre, che la corrente ai bordi fluisce anche in
assenza di un potenziale esterno che alimenti la corrente del sistema, ma che in questo caso le correnti ai lati
opposti del campione si annullano.
Nei sistemi n laboratorio si osserva che la corrente attraversa tutto il campione ma non in maniera
uniforme. Per studiarne l’andamento è necessario fare delle precisazioni:
a) Per spiegare la presenza di plateau nell’andamento della resistenza di Hall, dobbiamo assumere
la presenza di stati localizzati in tutto il campione.
b) Il livello di Fermi deve giacere tra i livelli di Landau: più precisamente l’energia di Fermi deve
ricadere in un intervallo diverso dall’energia degli stati estesi.
Se queste condizioni non si verificano, non possiamo trascurare la dispersione ai bordi opposti del campione.
Tuttavia, per un sistema ideale senza impurità, la densità degli stati ai bordi è molto ridotta rispetto a quella
del resto del sistema e le condizioni prima elencate sono verificate nel caso di quanti interi di ℎ⁄𝑒 2 .
Con un cambiamento del centro di coordinate da 𝑋 a 𝑙 e nel caso di una barriera di potenziale elevata,
l’energia degli stati di bordo varia di una quantità dell’ordine di ħ𝜔𝑐 . Pertanto, il rapporto tra il numero di
stati di bordo e quelli del restante sistema è 𝑙/𝐿 dove con 𝐿 sono indicate le dimensioni del campione.
Ricordandoci la relazione trovata per la resistenza di Hall nel caso dell’IQHE, i valori del fattore intero per cui
è verificata la condizione al punto b) è :
𝑁−𝑙
<𝑖<𝑁
𝐿
(3.3)
Dove con N è indicato il numero di stati di bordo, corrispondente al numero di livelli di Landau al di sotto
dell’energia di Fermi.
Fig.13 Vista dall’alto del flusso di corrente in un campione ideale. Nelle estremità del campione la
corrente risulta inclinata rispetto all’asse x.
Esiste tuttavia un limite per cui la dissipazione cresce di svariati ordini di grandezza: tale limite è detto
corrente critica 𝐼𝑐 e presenta una dipendenza dalla temperatura del sistema [3].
3.4 Effetti della temperatura
In tutto il capitolo secondo, riguardante la teoria alla base dell’IQHE, abbiamo sempre considerato il caso
ideale per la temperatura: lo zero assoluto. Come sappiamo, nei laboratori è impossibile ottenere questo
valore esatto, ma è possibile arrivare comunque a temperature al di sotto del Kelvin. Vediamo ora cosa
comporta questa correzione sulle caratteristiche del sistema viste finora. La temperatura ha degli effetti non
trascurabili sul moto elettronico e quindi sui livelli energetici: questo comporta delle variazioni della
[2] V.M. Pudalov and S.G. Semenchinskii, Pis’ma Zh. Eksp. Teor. Fiz.,1984
[3] G. Ebert, K.von Klitzing, C. Probst and K. Ploog, “Solid state communication” 44 95 ,1982 (JETP Letters)
28
resistività longitudinale 𝜌𝑥𝑥 , che nell’IQHE deve tendere a zero, e della corrente del sistema. Fino a 1 K questi
effetti risultano trascurabili e la teoria vista finora risulta adatta alla descrizione del sistema: infatti la
resistività longitudinale risulta talmente ridotta da renderne difficoltosa la stessa misura. Superato questo
valore però, si iniziano a osservare variazioni di queste grandezze dovute all’instabilità termica del sistema.
Infatti l’energia termica 𝑘𝑇 diventa rilevante e la resistività longitudinale presenta una dipendenza dalla
temperatura che va come:
∆𝐸
𝜌𝑥𝑥 ∝ exp (−
)
(3.4)
2𝑘𝑇
Dove con ∆𝐸 è indicata la separazione in energia tra i livelli di Landau.
Per un sistema Si MOSFET la resistività risulta minima per temperature inferiori ai 2 K; superati questi valori il
gap ∆𝐸 risulta pari all’85% dell’energia ciclotronica ħ𝜔𝑐 nel caso di 𝑖 = 2 e al 96% per 𝑖 = 4 [1]. Per
l’eterogiunzione 𝐺𝑎𝐴𝑠 − 𝐴𝑙𝐺𝑎𝐴𝑆 il gap risulta perfino superiore all’energia ciclotronica del 20% . Per la
separazione dei livelli dovuti al campo magnetico, ci si aspetterebbero valori inferiori di quelli appena citati.
Questo ci fa capire come in realtà in queste condizioni di temperatura siano importanti le interazioni fra gli
elettroni.
La temperatura ha effetti anche sulla resistenza di Hall. Intorno al 1983 si osservò che, misurando 𝜌𝑥𝑦 in
funzione dei valori del campo magnetico 𝐵 o della tensione applicata, corrispondenti a valori di minimo per
la resistenza longitudinale, la resistività di Hall presentava una dipendenza dalla temperatura [4]. Più
precisamente si osservò che all’aumentare della temperatura, 𝜌𝑥𝑦 diminuiva. La variazione
∆𝜌𝑥𝑦 = 𝜌𝑥𝑦 (𝑇) − 𝜌𝑥𝑦 (0) presentava infatti tale dipendenza:
∆𝜌𝑥𝑦 = −𝛼 𝜌𝑥𝑥
(3.5)
Dove il parametro 𝛼 dipende dal dispositivo usato.
Questa dipendenza è quindi lineare, come possiamo vedere dalla seguente figura:
Fig.14 Esempi della dipendenza lineare (3.5) in un’eterogiunzione 𝐺𝑎𝐴𝑠 − 𝐴𝑙𝐺𝑎𝐴𝑆 per temperature tra 1,2 − 3,0 𝐾.
[1] K. v Klitzing, G. Dorda, M. Pepper, “New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized
Hall Resistance”,1985, Phys. Rev. Lett. 45 494.
[4] K. Yoshihiro, J. Kinoshita, K. Inagaki , C. Yamanouchi , J. Moriyama and S. Kawaji, Physica B 117 706, 1983
29
È importante tuttavia notare che il meccanismo di questa relazione non è ancora stata spiegata.
La temperatura ha anche degli effetti, come accennato nel paragrafo precedente, sulla corrente che circola
nel sistema. Quando la tensione applicata aumenta improvvisamente, si va incontro a quello che viene
chiamato “breakdown” dell’IQHE: esiste un limite della corrente, la corrente critica 𝐼𝑐 , che provoca questa
variazione improvvisa della tensione.
Fig.15 Eterogiunzione 𝐺𝑎𝐴𝑠 − 𝐴𝑙𝐺𝑎𝐴𝑠 : 𝐼𝑐 ≈ 340 𝜇𝐴, 𝜌𝑥𝑥 aumenta di 7 ordini di grandezza a 1,2 K.
Tale valore risulta dipendente dalla larghezza del sistema e la densità di corrente critica di 0,5 − 2,0 𝐴⁄𝑚.
Invece di definire una corrente critica, è possibile esprimere il tutto in termini del campo elettrico: le due
grandezze sono infatti legate dalla conducibilità del sistema.
30
Conclusioni
Questo lavoro di tesi triennale ha lo scopo di introdurre i principi base e i principali sistemi in cui viene
sfruttato l’effetto Hall quantistico. Nel primo capitolo abbiamo introdotto le grandezze, quali la resistenza
Hall 𝑅𝐻 e la conducibilità, che sono alla base di tale fenomeno. Abbiamo in seguito, nel capitolo 2, spiegato i
principi della meccanica quantistica alla base di questo fenomeno quali la quantizzazione e la degenerazione
dei livelli energetici e di come questi siano, sotto certe condizioni, comparabili con quelli relativi ad un
oscillatore armonico. Abbiamo descritto gli effetti del disordine, identificato con le impurità e quindi il
drogaggio, del sistema in esame. Nel capitolo 3 abbiamo descritto i dispositivi più importanti in cui l’effetto
Hall quantistico viene sfruttato, partendo dal sistema Si MOSFET utilizzato nei primi esperimenti e
descrivendo poi un sistema più recente quale l’eterogiunzione 𝐺𝑎𝐴𝑠 − 𝐴𝑙𝐺𝑎𝐴𝑠. Infine sono stati descritti gli
effetti di bordo, dovuti alle dimensioni finite dei campioni, e della temperatura, descrivendo la tecnica più
comune utilizzata per raffreddare questi dispositivi: l’elio liquido.
Abbiamo visto quindi come l’effetto Hall quantistico sia un fenomeno, dai risvolti applicativi in ambito
elettrotecnico, fondamentale nell’ambito della fisica dello stato solido.
Lo sviluppo tecnologico permise, negli anni immediatamente successivi alla scoperta dell’effetto Hall
quantistico cosiddetto ordinario o intero, di realizzare campioni sempre più puliti. Investigando sulle
proprietà di questi nuovo campioni, nel 1982 i fisici Daniel Tsui e Horst Störmer scoprirono nuovi plateau
della conducibilità, pari a frazioni di 𝑒 2 ⁄ℎ: 1⁄3 e 2⁄3. Nel 1983 il fisico Robert Laughlin spiegò tale effetto
dal punto di vista teorico sfruttando un modello che tiene conto delle interazioni fra gli elettroni. Per la
scoperta di quello che viene chiamato effetto Hall quantistico frazionario, nel 1998 Tsui, Störmer e Laughlin
furono insigniti del premio Nobel per la fisica.
31
Bibliografia
[𝟏] Prof. Daijiro Yoshioka, The Quantum Hall Effect, Springer-Verlag Berlin Heidelberg, 2002.
[𝟐] Richard E. Prange auth., Steven M. Girvin eds. The Quantum Hall Effect, Springer-Verlag Berlin
Heidelberg, 1990.
[𝟑] http://www.damtp.cam.ac.uk/user/tong/qhe.html
[𝟒] http://www.nobelprize.org/nobel_prizes/physics/laureates/1985/press.html
[𝟓] https://en.wikipedia.org/wiki/Quantum_Hall_effect
32
Elenco figure
Fig.1 https://www.nobelprize.org/nobel_prizes/physics/laureates/1998/press.ht
Fig.2 www.fisica.unige.it/~mesoscop/Theses/Dolcetto_Diploma.pdf
Fig.3 https://www.nobelprize.org/nobel_prizes/physics/laureates/1998/press.ht
Fig.4 Prof. Daijiro Yoshioka, The Quantum Hall Effect
Fig.5 Richard E. Prange auth., Steven M. Girvin eds., The Quantum Hall Effect
Fig.6 Richard E. Prange auth., Steven M. Girvin eds., The Quantum Hall Effect
Fig.7 http://physicsresearchinbeijing.files.wordpress.com/2011/07/llqhe.gif
Fig.8 https://en.wikipedia.org/wiki/Quantum_Hall_effect
Fig.9 Prof. Daijiro Yoshioka, The Quantum Hall Effect
Fig.10 Prof. Daijiro Yoshioka, The Quantum Hall Effect
Fig.11 Prof. Daijiro Yoshioka, The Quantum Hall Effect
Fig.12 Prof. Daijiro Yoshioka, The Quantum Hall Effect
Fig.13 Richard E. Prange auth., Steven M. Girvin eds., The Quantum Hall Effect
Fig.14 Richard E. Prange auth., Steven M. Girvin eds., The Quantum Hall Effect
Fig.15 Prof. Daijiro Yoshioka, The Quantum Hall Effect
33
Ringraziamenti
Si conclude qui il percorso della laurea triennale. A questo punto mi sembra d’obbligo ringraziare tutti coloro
che mi hanno incoraggiato, sostenuto e accompagnato lungo questo percorso.
Il grazie più speciale va alla mia famiglia: mamma, papà, Chiara e perché no pure gatti. Senza il vostro
sostegno sarebbe stato tutto ancora più faticoso di quanto non lo sia stato. Ringrazio tutti i miei familiari,
che sono tanti, e gli amici di famiglia più cari.
Ringrazio il mio compagno di avventura Davide e gli amici più cari: Franci, Simo, Nico, Nunzia, Luca, Matteo,
Fabio, Marta e Vale per le risate, l’incoraggiamento e l’affetto che mi dimostrate tutti i giorni da anni.
Un altro grazie speciale va alla mia collega Chiara, perché senza la mia bacchettona preferita quest’anno non
sarei mai riuscita ad arrivare fino al primo (spero) traguardo. Ringrazio anche le mie colleghe, compagne di
tante avventure e disavventure Silvia L., Alexa, Maria Laura, Martina, Silvia C. e i colleghi Federico, Pietro,
Andrea.
Ringrazio tutti i docenti e i tutor incontrati, in particolar modo il professor Michele Saba, per la
professionalità e la disponibilità dimostrata in questi anni.