Esercizi-equazioni di stato:
Esercizi 2, 1
Esercizi 2, 2
Hp. Modellistica a)
Trascuriamo la temperatura di parete
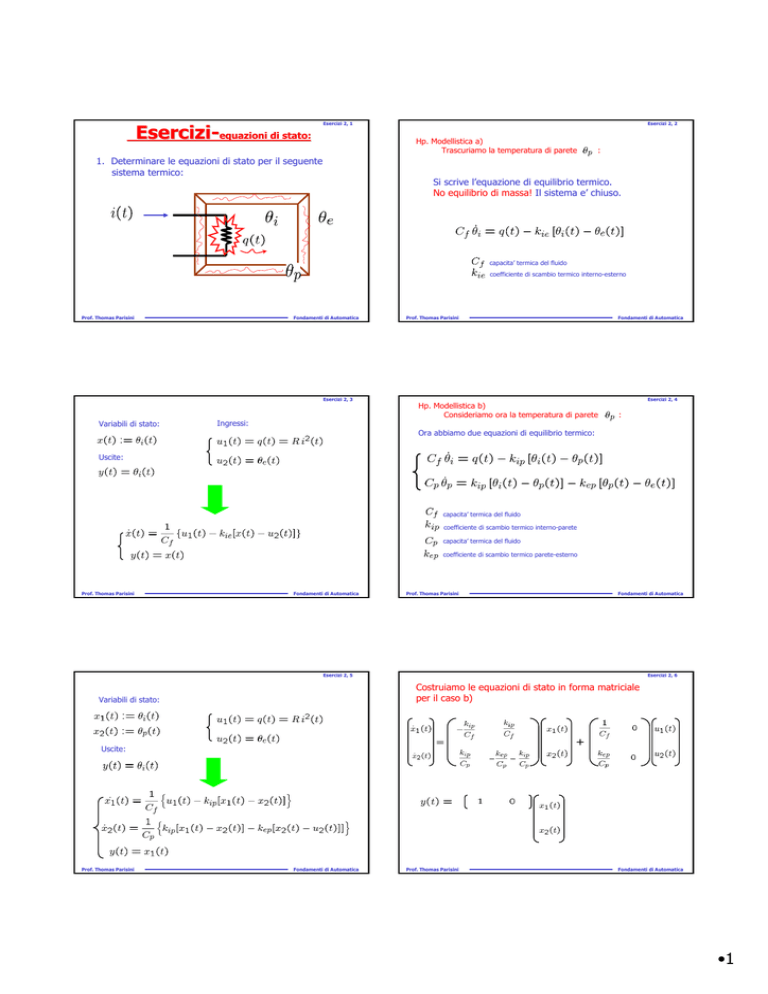
1. Determinare le equazioni di stato per il seguente
sistema termico:
:
Si scrive l’equazione di equilibrio termico.
No equilibrio di massa! Il sistema e’ chiuso.
capacita’ termica del fluido
coefficiente di scambio termico interno-esterno
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 3
Variabili di stato:
Ingressi:
Prof. Thomas Parisini
Hp. Modellistica b)
Consideriamo ora la temperatura di parete
Fondamenti di Automatica
Esercizi 2, 4
:
Ora abbiamo due equazioni di equilibrio termico:
Uscite:
capacita’ termica del fluido
coefficiente di scambio termico interno-parete
capacita’ termica del fluido
coefficiente di scambio termico parete-esterno
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 5
Esercizi 2, 6
Costruiamo le equazioni di stato in forma matriciale
per il caso b)
Variabili di stato:
Uscite:
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
•1
Esercizi 2, 7
2. Determinare delle equazioni di stato per il sistema
( piano inclinato senza attriti ) :
Esercizi 2, 8
Risultante su
:
Si considera come variabile da controllare l’altezza h della massa
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 9
In forma matriciale:
Esercizi 2, 10
Ma noi vogliamo osservare
s.d.r. del piano inclinato !
, non la posizione
nel
Ma poiche’:
Bastera’ effettuare una trasformazione del tipo :
Si potrebbe interpretare
come “disturbo
esterno”
Prof. Thomas Parisini
Fondamenti di Automatica
con :
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 11
Esercizi per casa...
Esercizi 2, 12
2. Mettere in equazioni di stato il seguente sistema:
1. Antitrasformare le funzioni:
•
•
•
•
Prof. Thomas Parisini
Fondamenti di Automatica
Suggerimenti:
Scrivere i principi di Kirchhoff ai nodi e alle maglie.
Prendere come variabili di stato le grandezze associate a
condensatori (tensione) ed induttanze (correnti).
Ingresso: corrente entrante al nodo A
Uscita: tensione sul condensatore
Prof. Thomas Parisini
Fondamenti di Automatica
•2
Esercizi 2, 13
Esercizi - linearizzazione:
3. Mettere in equazioni di stato il seguente sistema:
Esercizi 2, 14
1. Determinare le equazioni di stato per il seguente
sistema e linearizzarlo intorno ad un punto di
equilibrio:
•
•
•
•
Suggerimenti:
Scrivere i principi di Kirchhoff ai nodi e alle maglie.
Prendere come variabili di stato le grandezze associate a
condensatori (tensione) ed induttanze (correnti) Æ avremo tre
variabili di stato, sistema tre per tre!
Ingresso: tensione fra A e B
Uscita: tensione sulla resistenza
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 15
Dove si specificano il coefficiente di attrito radente
e la forza della molla, entrambi non lineari:
Esercizi 2, 16
Che si puo’ riscrivere cosi’:
Variabili di stato:
Risultante delle forze su
Ingresso:
:
Uscite:
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 17
Esercizi 2, 18
Da cui si ricavano le equazioni di stato linearizzate intorno al
punto trovato:
Dunque sostituendo ricaviamo le seguenti
equazioni:
Imponiamo un ingresso costante
e cerchiamo il punto di
equilibrio, in cui entrambe le derivate si annullano:
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
•3
Esercizi 2, 19
Esercizi 2, 20
2. Mettere in equazioni di stato il seguente sistema, in cui
e’ presente un elemento non lineare:
Da cui si ricava, sostituendo, il seguente sistema matriciale:
Che vale per piccole perturbazioni intorno al punto di equilibrio
trovato.
Secondo principio di Kirchhoff:
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 21
Come al solito, prendiamo come variabili di stato le correnti nelle
induttanze e le tensioni sui condensatori:
Esercizi 2, 22
Percio’ le equazioni di stato del sistema sono:
E sono non lineari in
Ricaviamo dunque
stato:
e
. Ponendo per semplicita’ :
in funzione delle sole variabili di
Dunque linearizziamo il sistema intorno ad un punto di equilibrio,
scegliendo come ingresso un valore costante di tensione.
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 23
Prendiamo ad esempio
e calcoliamo i valori di
quando le derivate si annullano.
e
Dunque calcoliamo le matrici del sistema linearizzato intorno a questo
punto:
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 24
Da cui si ricava, sempre sostituendo, il seguente sistema
matriciale:
Che, ancora una volta, vale per piccole perturbazioni intorno al
punto di equilibrio trovato.
Prof. Thomas Parisini
Fondamenti di Automatica
•4
Esercizi 2, 25
Esercizio per casa...
Esercizi 2, 26
Linearizzare il sistema a partire dalle equazioni di stato che
verranno di seguito ricavate. NB: stavolta non serve
scrivere le equazioni ai nodi o alle maglie...
Possiamo ricavare immediatamente delle equazioni di stato in
funzione delle sole
e
. Infatti:
Elemento passivo
non lineare
Prof. Thomas Parisini
Fondamenti di Automatica
Prof. Thomas Parisini
Fondamenti di Automatica
Esercizi 2, 27
Dunque sostituendo si ha:
Non lineare! Cosa resta da fare?
Cerchiamo una soluzione particolare, ad esempio
cortocircuitiamo l’ingresso:
In corrispondenza a questo ingresso azzeriamo le derivate
ed
e troviamo
ed
.
Si deve trovare
ed
... poi si calcolano le
matrici del sistema linearizzato come gia’ fatto!
Prof. Thomas Parisini
Fondamenti di Automatica
•5