la coerenza della luce

LA COERENZA DELLA LUCE
COERENZA PARZIALE
onda piana
onda
sferica
S
f
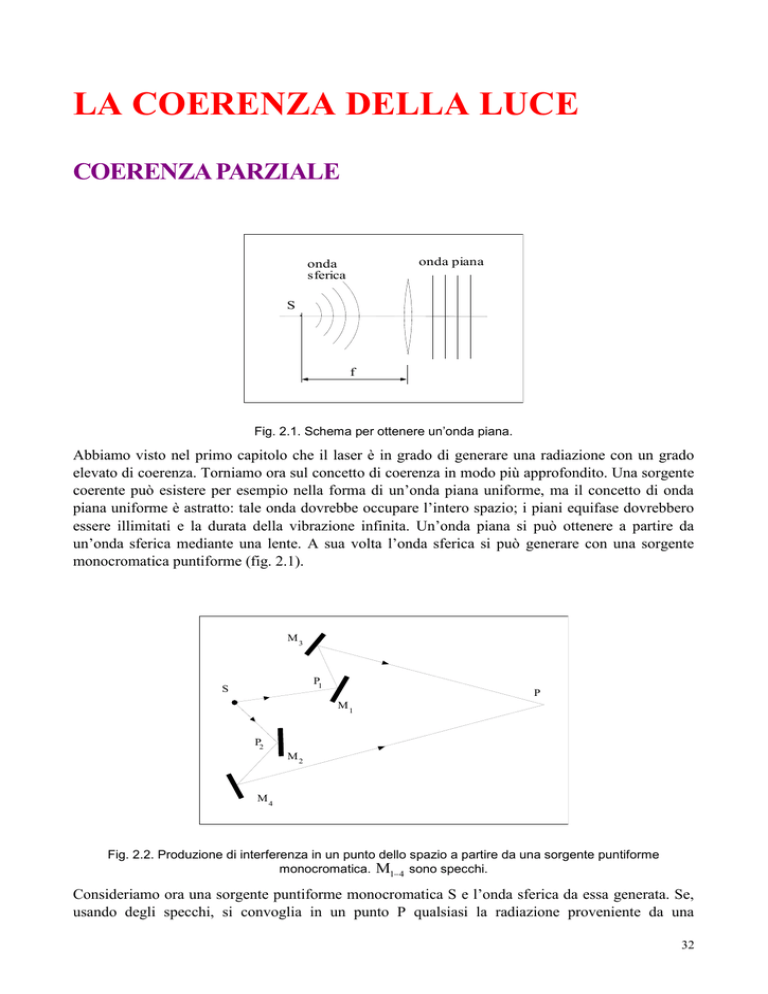
Fig. 2.1. Schema per ottenere un’onda piana.
Abbiamo visto nel primo capitolo che il laser è in grado di generare una radiazione con un grado
elevato di coerenza. Torniamo ora sul concetto di coerenza in modo più approfondito. Una sorgente
coerente può esistere per esempio nella forma di un’onda piana uniforme, ma il concetto di onda
piana uniforme è astratto: tale onda dovrebbe occupare l’intero spazio; i piani equifase dovrebbero
essere illimitati e la durata della vibrazione infinita. Un’onda piana si può ottenere a partire da
un’onda sferica mediante una lente. A sua volta l’onda sferica si può generare con una sorgente
monocromatica puntiforme (fig. 2.1).
M3
P1
S
P
M1
P2
M2
M4
Fig. 2.2. Produzione di interferenza in un punto dello spazio a partire da una sorgente puntiforme
monocromatica. M14 sono specchi.
Consideriamo ora una sorgente puntiforme monocromatica S e l’onda sferica da essa generata. Se,
usando degli specchi, si convoglia in un punto P qualsiasi la radiazione proveniente da una
32
qualunque coppia di punti dello spazio P1 , P2 , si ottiene un’interferenza, cioè il sommarsi in
ampiezza complessa della radiazione proveniente dai due punti (fig. 2.2).
L’interferenza è ottenibile in tutte le regioni dello spazio in cui si fanno interferire le vibrazioni. Si
dice che una sorgente puntiforme monocromatica, e quindi un’onda sferica ideale, da dei fenomeni
di interferenza non localizzati. Anche un’onda piana uniforme da luogo a dei fenomeni di
interferenza non localizzati.
Per i campi generati dalle sorgenti ordinarie questa possibilità è esclusa; si dice che le sorgenti reali
sono parzialmente coerenti. La parzialità della coerenza limita la possibilità di ottenere dei
fenomeni di interferenza tra punti qualsiasi dello spazio. Si possono distinguere due concetti: la
coerenza temporale e la coerenza spaziale. La coerenza temporale è legata alla durata (o lunghezza)
dei treni d’onda elettromagnetici emessi dalla sorgente mentre la coerenza spaziale è legata alle
dimensioni della sorgente stessa.
COERENZA TEMPORALE
Per spiegare questo concetto descriviamo prima il dispositivo noto come interferometro di
Michelson. Esso è costituito da un divisore di raggio D e da due specchi piani M1 ed M2 . I due
specchi sono perpendicolari l’uno all’altro e la superficie semiriflettente del divisore di raggio è
inclinata di 45 rispetto alle normali a M1 ed M2 . Il divisore di raggio riflette tanta luce quanta ne
trasmette.
M1
A1
(a)
S
I
(b)
A2
M2
D

T
d
osservatore
Fig. 2.3. Interferometro di Michelson.
Sia  un’onda piana uniforme (quindi monocromatica) di lunghezza d’onda  con la stessa giacitura
di M2. Per semplicità consideriamo il raggio SI. Quando esso arriva sulla superficie semiriflettente
del divisore si separa in due raggi che hanno i seguenti tragitti:

tragitto 1
IA1IT
33

tragitto 2
IA2IT
I due raggi si sovrappongono in T dove interferiscono. Si vede facilmente che la differenza di
cammino dei due raggi è pari a 2d. Si dimostra che, se I0 è l’intensità del raggio entrante, l’intensità
dell’interferenza in T è data da
2
I  I0 cos2
d

(2.1)
Ad esempio se d è un multiplo dispari di /4 si ha interferenza distruttiva.
L’interferometro sia ora illuminato da un’onda piana generata a partire da una sorgente puntiforme
non monocromatica. A differenza del caso di perfetta monocromaticità, i treni d’onda hanno una
durata (lunghezza) limitata. Un treno d’onda incidente è diviso in due treni d’onda che seguono i
cammini (a) e (b) (fig. 2.4). I due treni d’onda, provenienti dallo stesso treno d’onda iniziale, non si
sovrappongono all’uscita dell’interferometro se la differenza di cammino è più grande della loro
lunghezza (detta lunghezza di coerenza).
M1
(a)
(b)
M
D
2
d
osservatore
Fig. 2.4. La differenza di cammino è tale che all’osservatore giungono treni d’onda diversi.
Ci possono essere dei treni d’onda che si sovrappongono ma allora essi provengono da due treni
d’onda iniziali diversi. Essendo l’emissione degli atomi aleatoria, la differenza di fase tra i treni
d’onda che si sovrappongono all’uscita dell’interferometro è aleatoria. In questa situazione
l’interferenza non è più osservabile: si sommano le intensità e non le ampiezze. Si dice che c’è
incoerenza temporale. Affinché sia visibile l’interferenza bisogna che la differenza di cammino sia
più piccola della lunghezza di coerenza.
Si può dimostrare che la durata media  di un treno d’onda (detta tempo di coerenza) è legata alla
larghezza di banda spettrale  della sorgente dalla relazione

1

(2.2)
Quindi la lunghezza di coerenza vale
34
l = c =
c

(2.3)
La lunghezza di coerenza della luce bianca è estremamente piccola e vale circa 1 m.
Apriamo ora una piccola parentesi. Vogliamo trovare una semplice relazione scalare per descrivere
un treno d’onda quasi monocromatico. Descriviamo un treno d’onda con la funzione u(t)
caratterizzata dallo spettro U(  ) :
U(  ) = 
+
u(t)e -j2t dt
-
(2.4)
e dunque
u(t) = 
+
U( 
-
)e j2t d
(2.5)
Lo spettro U(  ) caratterizza l’ampiezza e la fase di ciascuna componente monocromatica
contenuta in u(t). Se U(  ) non differisce da zero che per dei valori di  vicini ad un valor
medio  0 è comodo scrivere u(t) nella forma seguente:
u(t) = e j2 0 t 
+
U( 
-
)e j2 (    0 )t d
(2.6)
e ponendo
a(t) = 
+
U( 
-
)e j2 (    0 )t d
(2.7)
si ha
u( t )  a( t )e j 2 0 t
(2.8)
L’ampiezza complessa a(t) varia lentamente relativamente al periodo vibratorio T = 1/ 0 . L’onda
u(t) è detta vibrazione quasi monocromatica. Essa differisce da una vibrazione monocromatica
e j 20t per la presenza del fattore a(t).
COERENZA SPAZIALE
Per spiegare questo concetto ci basiamo sull’esperimento di interferenza di Young. La sorgente di
luce sia estesa, piana, incoerente e quasi monocromatica (di frequenza media 0 ). Essa può essere
pensata come costituita da innumerevoli sorgenti puntiformi incoerenti. La quasi monocromaticità è
richiesta per non preoccuparsi della lunghezza di coerenza: la coerenza temporale è supposta
sufficientemente elevata da permettere l’interferenza in qualunque punto della limitata regione di
osservazione. La sorgente illumina uno schermo opaco con due piccoli forellini nei punti Q 1 e Q2.
Nel discorso che segue Q1 e Q2 indicano sia i punti che i forellini. La luce che passa attraverso i
forellini raggiunge il piano di osservazione dove si possono formare delle frange di interferenza. Il
contrasto delle frange dipende dalla posizione dei forellini e dalla distribuzione dell’intensità
luminosa della sorgente. In figura 2.5 è mostrato lo schema dell’esperienza di Young.
35

intensità delle
frange
y
Q
y'
P
1
S
Q2

x'
x
r2
r1
piano di osservazione
piano della sorgente
Fig. 2.5. Esperienza di Young
Per semplicità si fa l’ipotesi che la distanza d tra Q1 e Q2 sia molto minore delle distanze r1 e r2.
Per la misura del contrasto delle frange si adotta il parametro
I
I
V  max min
I max  I min
(2.9)
detto visibilità di Michelson delle frange. Consideriamo le onde emesse allo stesso istante da Q1 e
Q2. La vibrazione emessa da Q1 in P all’istante t sia rappresentata dall’ampiezza complessa a1(t).
All’istante t l’onda emessa da Q2 non è in P ma ad esempio in P' (fig. 2.6) e la sua ampiezza è a 2 (t).
piano di osservazione

Q
1
P'
S
Q2
P
r2
Fig. 2.6. Interferenza in P delle onde emesse da Q1 e Q2.
Allora l’ampiezza di a2 (t) in P all’istante t è quella che era in P' all’istante t-; dunque in P
all’istante t è rappresentata dall’espressione a 2 (t -  )e- j2 0 dove  è il tempo impiegato dall’onda
per andare da P' a P. Se  è la distanza tra P e P' allora  = /c. Come già detto le ampiezze
complesse a1 (t) e a2 (t) variano lentamente in rapporto al periodo T dell’onda quindi si può porre
a2(t-)  a2 (t) . L’ampiezza complessa in P risulta
a ( t )  a1 (t) + a 2 (t)e- j2 0
(2.10)
A parte un fattore costante l’intensità media relativa a un periodo di osservazione lungo rispetto alla
durata dell’onda risulta:
36
I   a ( t ) a* ( t )   [ a1 (t) + a 2 (t)e- j2 0 ][ a1* (t) + a*2 (t)e+ j2 0  ]
(2.11)
Poniamo e j2 0   e j :  è la differenza di fase in P tra le onde inviate da Q1 e Q2; tale differenza
dipende dalla posizione di P. Si ha
I   a1a1*    a 2a*2    a1*a 2 e j   a1a*2 e j
(2.12)
I primi due addendi rappresentano le intensità I1 e I2 prodotte da Q1 e Q2 agenti separatamente. Si
può scrivere:
I  I1  I2  2 Re{ a1a*2e j }
(2.13)
Definiamo ora grado di coerenza complesso delle vibrazioni emesse da Q1 e Q2 la quantità  a 1a *2 
normalizzata rispetto alle intensità
 12 
 a 1 ( t ) a *2 ( t ) 
I 1I 2
(2.14)
Vale   12 1. Esprimendo  12 in modulo e fase
 12   12 e j
(2.14)
I  I 1  I 2  2 I 1I 2  12 cos(    )
(2.15)
e sostituendo nella 2.13 si ottiene
Per comprendere il significato del grado di coerenza calcoliamo, basandoci sulla precedente
relazione, la visibilità delle frange nel caso I1 = I2, detto condizione migliore in cui
I min  2 I  2 I   12 
I max  2 I  2 I   12 
V
4 I  12
  12
4I
(2.16)
Ecco che il modulo del grado di coerenza complesso da la visibilità delle frange nella condizione
migliore. Ci sono tre casi da considerare:
  12  = 1.
Le radiazioni emesse da Q1 e Q2 sono coerenti.
  12  = 0.
Le radiazioni emesse da Q1 e Q2 sono incoerenti. La 2.15 diventa I = I1+I2: non si ha alcuna
interferenza e le intensità si sommano.
37
  12 <1.
Le radiazioni emesse da Q1 e Q2 sono parzialmente coerenti e   12  misura la visibilità delle frange
nella condizione migliore.
APPLICAZIONE DEL CONCETTO DI COERENZA SPAZIALE AI SISTEMI
OTTICI
Prima di proseguire facciamo alcune considerazioni. Il grado di coerenza è funzione della posizione
di Q1 e Q2 e della ripartizione dell’intensità di emissione della sorgente. Esso è una proprietà fisica
di un campo elettromagnetico in due punti; nel caso che ci interessa i due punti appartengono ad un
piano parallelo al piano che contiene la sorgente (piana). Il grado di coerenza di una coppia di punti
da una misura della capacità di interferire della radiazione che attraversa quei punti. Lo schermo
dell’esperimento di Young, con i forellini nei due punti considerati, è il mezzo che creando delle
frange su un piano di osservazione, permette una misura del grado di coerenza.
Esiste un risultato teorico molto importante, il teorema di Van Cittert - Zernike, che ci permette di
calcolare il grado di coerenza tra due punti Q1,Q2 illuminati da una sorgente estesa piana e quasi
monocromatica. Q1,Q2 appartengono ad un piano parallelo al piano della sorgente (fig. 2.7).

y
Q1
S

x
Q2
d
Fig. 2.7. Situazione geometrica cui si applica il teorema di Van Cittert - Zernike
Supponiamo valga l’ipotesi parassiale, cioè che la distanza Q1Q 2 e le dimensioni della sorgente
siano piccole rispetto alla distanza d tra la sorgente e il piano che contiene Q1 e Q2. Le coordinate di
Q1 e Q2 siano rispettivamente ( x1 , y1 ) e ( x 2 , y 2 ) .
Il teorema di Van Cittert - Zernike afferma che
 12 ( Q1Q2 )   12 ( x1 , y1 ; x2 , y2 ) 
 J ( 
k
j [  ( x1  x 2 ) ( y1  y 2 )]
d
, )e
d
d
 J (  , )d d
(2.17)
38
dove J(,) è la ripartizione dell’intensità di emissione della sorgente. La relazione 2.17 mostra che
il grado di coerenza complesso tra due punti illuminati da una sorgente estesa S è dato
dall’antitrasformata di Fourier normalizzata della funzione J( , ) .
In molti testi si definisce un grado di coerenza non normalizzato 12; al posto della 2.14 si definisce
12   a1 ( t ) a *2 ( t ) 
(2.14')
Il teorema di Van Cittert - Zernike per la funzione di coerenza non normalizzata è
12 ( x1 , y1 ; x2 , y2 ) 

1
d2
k
j [  ( x1  x 2 ) ( y1  y 2 )]
J (  , )e d
dd
(2.17')
Nei sistemi ottici di elaborazione è richiesto che l’immagine sia attraversata da un’onda piana; in
pratica si vuole che il campo sia caratterizzato da un grado di coerenza unitario per ogni coppia di
punti dell’immagine. In questo modo si ottiene la linearità in ampiezza complessa del sistema. Non
sempre è richiesto un grado di coerenza elevato tra ogni coppia di punti dell’immagine: ad esempio
nel sistema ottico per la sottrazione di immagine è richiesto un grado di coerenza elevato solo tra le
coppie di punti che si corrispondono nelle immagini di ingresso.
In pratica l’illuminazione in un sistema ottico di elaborazione parzialmente coerente non è
realizzata illuminando direttamente l’immagine come schematizzato in figura 2.7. La radiazione
emessa dalla sorgente viene collimata con una lente sul piano di ingresso (in cui è collocata
l’immagine da elaborare) (fig. 2.8a). Inoltre la sorgente può essere codificata con una opportuna
maschera la cui trasparenza modula l’intensità luminosa della sorgente stessa (fig. 2.8b).

y
PI
Po
J( 
S

x
f
f
Fig. 2.8a. La radiazione emessa dalla sorgente viene collimata da una lente sul piano di ingresso del
sistema di elaborazione.
39
maschera
codificante
la sorgente

PI
y
J( 
S
 Po
x
f
f
Fig. 2.8b. La radiazione emessa dalla sorgente viene codificata da una maschera, prima di essere collimata
dalla lente sul piano di ingresso del sistema di elaborazione.
In entrambi i casi la distribuzione dell’intensità luminosa sul piano P0 sia data da J(,). Per
semplificare la scrittura rappresentiamo i punti del piano P0 con il vettore  e quelli del piano

dell’immagine con x . Si dimostra che il grado di coerenza per le coppie di punti del piano PI è dato
da
k  

 j  ( x1  x 2 ) 
 


 ( x1 , x2 )   ( x1  x2 )   J   e f
d
(2.18)
Il grado di coerenza risulta essere la IFT della distribuzione dell’intensità luminosa J( , ) . Quindi,
in forma compatta valgono le



 ( x1  x2 )  IFT J   



 
J     FT   ( x1  x2 )
(2.19)
Ad esempio nel caso particolare di sorgente puntiforme data da J( , ) = K(,) il modulo del
grado di coerenza risulta


 ( x1  x2 )  K1
con K1 costante. Si è nel caso di perfetta coerenza spaziale. È questo che si cerca di ottenere
nell’elaborazione coerente tradizionale (fig. 2.9)
40
maschera
codificante
la sorgente
fascio laser espanso

J(  
x,y

LASER
fascio laser
Po
PI
Fig. 2.9. Sistema di illuminazione impiegato nell’elaborazione coerente.
Nel caso di fig. 2.9 la maschera codificante la sorgente è un forellino (pinhole): tanto minore è il
diametro del pinhole tanto maggiore è il grado di coerenza che si riesce ad ottenere, ma tanto
maggiore è anche il sacrificio dell’intensità luminosa disponibile. Esistono casi (esempio
sottrazione di immagini) in cui un’opportuna codifica della sorgente è in grado di fornire il grado di
coerenza spaziale sufficiente, permettendo uno sfruttamento migliore della luminosità della
sorgente.
ELABORAZIONE OTTICA IN LUCE BIANCA
Per l’elaborazione ottica delle immagini possono venire impiegati sistemi che utilizzano una
sorgente di luce bianca. Un vantaggio dei sistemi di elaborazione in luce bianca è la facile
reperibilità della sorgente luminosa e il suo minor costo rispetto ai laser necessari nell’elaborazione
coerente e l’introduzione del colore nell’elaborazione ottica. Le sorgenti di luce bianca più indicate
ad essere impiegate nei sistemi ottici di elaborazione sono quelle alogene e quelle ad arco per
l’elevata brillanza della radiazione emessa. Nell’esempio mostrato più avanti (figg. 2.11, 2.12) la
sorgente utilizzata è una lampada ad arco corto in Xeno della potenza di 75 Watt. La piccola
dimensione dell’arco consente di ottenere dei fasci di luce ben collimati. Lo schema impiegato per
generare il fascio è il seguente:
PI
fascio
collimato x,y
catodo
pinhole
sorgente
P
S
anodo
0
f
Fig. 2.10. Schema utilizzato in laboratorio per generare il fascio collimato di luce bianca.
Il pinhole realizza una maschera di codifica della sorgente; tanto più è piccolo tanto più approssima
una sorgente puntiforme, aumentando così la coerenza spaziale. Il fascio di luce che si ottiene è
41
adatto ad essere impiegato in un sistema ottico di elaborazione. Nel discorso che segue facciamo
riferimento allo schema ottico di elaborazione a due lenti [1]. Sia le lenti impiegate per generare il
fascio collimato che quelle impiegate nel sistema ottico di elaborazione devono essere acromatiche
altrimenti l’intero sistema risulta affetto da aberrazione cromatica. L’immagine da elaborare, posta
anteriormente alla lente di trasformazione, può essere ad esempio una diapositiva colorata. In
generale la sua trasparenza dipende anche dalla lunghezza d’onda. Nell’ipotesi che la sorgente sia
codificata con un pinhole così piccolo da poterlo pensare equivalente ad una sorgente puntiforme,
sul piano di Fourier della lente di trasformazione si ottiene, per ogni lunghezza d’onda , un campo
d’onda complesso dato da:
F (  ,  ;  )  S (  ) f ( x , y ;  )e
j
2
( x  y )
f
dxdy
(2.20)
dove S() è la distribuzione spettrale della sorgente impiegata e f(x,y;) è la trasparenza
dell’immagine in corrispondenza alla lunghezza d’onda . Come noto dai principi dell’elaborazione
ottica delle immagini, la lunghezza d’onda introduce un fattore di scala sulla dimensione della
trasformata. Quindi, operando in luce bianca, sul piano di Fourier si forma una sovrapposizione di
trasformate, una per ogni lunghezza d’onda: le trasformate nella lunghezza d’onda del blu sono più
piccole di quelle nel rosso. Indicheremo tale sovrapposizione di trasformate come trasformata
(ottica) colorata.
Fig. 2.11a. Immagine di prova.
42
Fig. 2.11b. Trasformata di Fourier colorata dell’immagine di prova.
La trasformata di fig. 2.11b è stata ottenuta impiegando un pinhole di 25 m di diametro. Se la
maschera codificante la sorgente non è un piccolo forellino (in pratica la maschera equivale ad una
sorgente estesa) diminuisce la coerenza spaziale. Si ottiene una sovrapposizione di trasformate
colorate, una per ogni sorgente elementare in cui si può pensare di scomporre la sorgente estesa. La
figura 2.12 mostra lo spettro dell’immagine di prova ottenuto usando un forellino di 500 m.
Tralasciamo, per semplicità, l’espressione del campo che si ottiene sul piano della trasformata.
Fig. 2.12. Immagine sul piano della trasformata nel caso di bassa coerenza spaziale.
Per ottenere l’elaborazione dell’immagine è necessario collocare un filtro sul piano della
trasformata. Con riferimento al sistema ottico di elaborazione a due lenti e nell’ipotesi di sorgente
puntiforme, la distribuzione dell’intensità luminosa sul piano dell’immagine ricostruita è data da

I ( x' , y' )   R S (  )  F(  ,  ;  ) H (  ,  )e
B
j
2
( x'  y' )
f
2
dd d
(2.21)
dove H(,) rappresenta la trasparenza del filtro collocato nel piano della trasformata e  B ,  R sono
le lunghezze d’onda della luce agli estremi della banda del visibile. L’azione del filtro è diversa per
ogni lunghezza d’onda a causa del fattore di scala che la lunghezza d’onda stessa introduce sulla
43
dimensione della trasformata. Questo comporta una grande difficoltà nella realizzazione dei filtri
quando si vogliano realizzare filtraggi che agiscano nello stesso modo sulle frequenze spaziali
dell’immagine, indipendentemente dalla lunghezza d’onda della luce. La difficoltà nella
realizzazione dei filtri per generiche elaborazioni ottiche in luce bianca costituisce il principale
svantaggio di tale tipo di illuminazione rispetto ai tradizionali sistemi in luce coerente. Sono state
proposte diverse tecniche per aggirare tale problema; comunque la descrizione di esse esula dagli
scopi di questa trattazione. In alcuni casi, come per esempio la visualizzazione delle immagini di
fase in luce bianca [2], il problema di filtrare in modo omogeneo le componenti armoniche delle
immagini stesse non sussiste: la particolare struttura dei filtri impiegati evita il problema. Questo
fatto permette una facile estensione delle tecniche di visualizzazione delle immagini di fase ai
sistemi ottici di elaborazione in luce bianca.
Nonostante il problema del filtraggio i sistemi di elaborazione ottica in luce bianca offrono alcuni
notevoli vantaggi rispetto ai sistemi in luce monocromatica. Uno dei miglioramenti più evidenti è la
soppressione quasi totale del rumore di coerenza. Infatti un sistema ottico di elaborazione coerente è
costituito da un unico canale di trasmissione, dato dall’unica lunghezza d’onda e dall’unico punto di
emissione della sua sorgente di luce; così, se in un punto qualsiasi del sistema si crea un disturbo,
esso fa inevitabilmente perdere dell’informazione dando luogo a delle immagini rumorose. Invece
un elaboratore ottico in luce bianca può essere visto come un sistema a più canali non correlati: la
mancanza di coerenza temporale indica che l’informazione è trasmessa da innumerevoli bande
spettrali elementari, costituenti ciascuna un canale di trasmissione indipendente. Allo stesso modo
la parziale coerenza spaziale indica che la sorgente ha una superficie di emissione estesa che può
essere scomposta in più sorgenti elementari, ciascuna delle quali costituisce un canale di
trasmissione indipendente. Quindi se un disturbo fa perdere dell’informazione in un canale del
sistema, essa viene degradata solo in parte essendo presente anche su altri canali.
Paragrafo successivo
Paragrafo precedente
Indice del capitolo
Indice generale
44