1. LA CONTINUITAÁ CON GEOGEBRA E WIRIS
Sia con GeoGebra che con Wiris, per studiare la continuitaÁ di una funzione dobbiamo sostanzialmente ricorrere al calcolo dei limiti che abbiamo imparato nel precedente capitolo.
Nelle due esercitazioni che ti proponiamo abbiamo individuato i punti di discontinuitaÁ della funzione
8 2
x
2x0
<x
3
y x x
0<x2
:
5 x
2<x6
Usiamo GeoGebra
Per scrivere l'equazione della funzione dobbiamo usare il comando Funzione che ha la seguente sintassi
Funzione [Funzione, Valore x iniziale, Valore x finale]
dove il parametro Funzione rappresenta l'espressione di f
x , i parametri Valore x iniziale e Valore x finale rappresentano rispettivamente l'estremo sinistro e l'estremo destro dell'intervallo di definizione della funzione.
Definiamo dunque le tre espressioni della funzione scrivendo:
Funzione x^2
x,
2, 0
Funzione x^3 x, 0, 2
Funzione 5
x, 2, 6
Nella Vista Algebra alle tre funzioni viene attribuito nome rispettivamente f
x , g
x e h
x e viene disegnato il grafico di
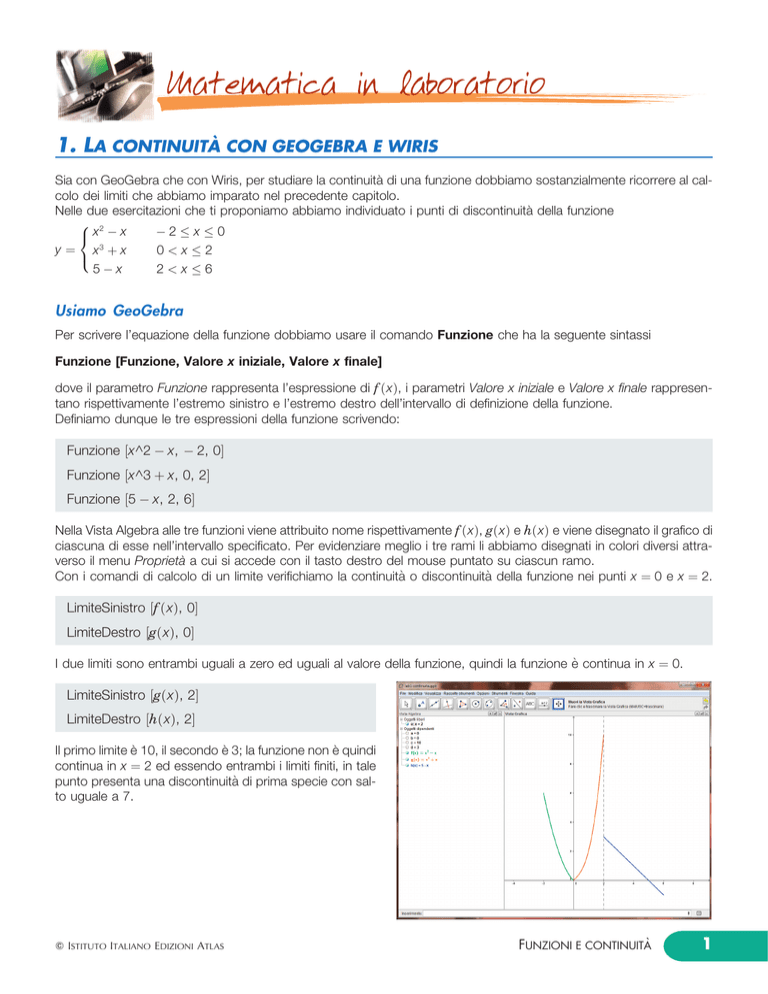
ciascuna di esse nell'intervallo specificato. Per evidenziare meglio i tre rami li abbiamo disegnati in colori diversi attraverso il menu ProprietaÁ a cui si accede con il tasto destro del mouse puntato su ciascun ramo.
Con i comandi di calcolo di un limite verifichiamo la continuitaÁ o discontinuitaÁ della funzione nei punti x 0 e x 2.
LimiteSinistro f
x , 0
LimiteDestro g
x , 0
I due limiti sono entrambi uguali a zero ed uguali al valore della funzione, quindi la funzione eÁ continua in x 0.
LimiteSinistro g
x , 2
LimiteDestro h
x , 2
Il primo limite eÁ 10, il secondo eÁ 3; la funzione non eÁ quindi
continua in x 2 ed essendo entrambi i limiti finiti, in tale
punto presenta una discontinuitaÁ di prima specie con salto uguale a 7.
Q ISTITUTO ITALIANO EDIZIONI ATLAS
FUNZIONI E CONTINUITAÁ
1
Usiamo Wiris
Definire una funzione per casi con Wiris eÁ leggermente piuÁ complesso ed eÁ necessario introdurre la funzione controlla
per specificare l'intervallo di definizione.
Osserva il seguente comando:
f
x controlla
x 2 ^ x 0 : x 2
x
Con questa scrittura si eÁ specificato che la funzione f eÁ definita dall'espressione x 2 x solo per i valori di x che sono
contemporaneamente maggiori o uguali di 2 e minori o uguali a 0, cioeÁ nell'intervallo 2 x 0.
La funzione controlla deve essere scritta subito dopo il nome della funzione e prima del simbolo di assegnamento :.
Per completare la definizione della funzione f si devono poi specificare le altre espressioni, ciascuna nell'intervallo di
pertinenza, con la stessa modalitaÁ.
Il comando
definizione
f
consente poi di rivedere per intero la definizione della funzione. A questo punto eÁ possibile tracciarne il grafico.
Studiamo adesso la continuitaÁ della funzione nei punti x 0 e x 2.
Questa modalitaÁ di definizione permette di valutare la funzione in un punto, ma non consente di calcolarne i limiti.
Possiamo quindi calcolare f
0 e f
2, ma dobbiamo ridefinire le tre espressioni come tre funzioni diverse; nella figura
sono le funzioni indicate con g
x, h
x e k
x .
Sappiamo poi come calcolare i limiti sinistro e destro per x ! 0 e per x ! 2.
Dai risultati ottenuti dobbiamo concludere che la funzione eÁ continua in x 0 e presenta una discontinuitaÁ di prima
specie in x 2.
2. GLI ASINTOTI
Usiamo GeoGebra
La ricerca degli asintoti con GeoGebra avviene con il comando
Asintoto [funzione]
Viene cosõÁ restituita la lista di tutti gli asintoti della funzione specificata.
2
FUNZIONI E CONTINUITAÁ
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Per esempio, applicando questo comando alla funzione f
x
lista =f x y
2, x
1g
x2 x
si ottiene come risultato:
x1
l
nella Vista Algebra:
l
nella Vista Grafica la rappresentazione grafica delle rette asintoto.
Il comando non opera peroÁ su funzioni piuÁ complesse quali le funzioni logaritmiche oppure esponenziali.
Usiamo Wiris
Il tracciamento del grafico di una funzione con il comando rappresentare permette di mettere in evidenza le caratteristiche fondamentali della funzione, compresi i suoi asintoti; prova ad usare questo comando scrivendo
rappresentare
x2 x
x1
I comandi specifici per la rappresentazione degli asintoti sono i seguenti e prevedono anche l'assegnazione di un colore
specifico (quelli da noi scelti sono del tutto arbitrari):
rappresentare (funzione, fasintoto orizzontale = fcolore = blugg)
rappresentare (funzione, fasintoto verticale = fcolore = rossogg)
rappresentare (funzione, fasintoto obliquo = fcolore = verdegg)
Non esistono invece comandi che restituiscono le equazioni degli asintoti; esse possono essere calcolate con le procedure studiate.
Q ISTITUTO ITALIANO EDIZIONI ATLAS
FUNZIONI E CONTINUITAÁ
3












