Circuitazione di Ampere

Il teorema della circuitazione di Ampere
(quarta equazione di Maxwell)
S.Sarti
Introduzione
Nel caso del campo elettrico, alla legge di Gauss relativa al flusso del campo
elettrico attraverso una superficie chiusa (Legge di Gauss) si affiancava una
seconda relazione integrale che esplicitava il carattere conservativo del campo
elettrico, ovvero
I
~ · d~` = 0
E
C
~ = ∇
~ ∧E
~ = 0. In questo caso, il
che è equivalente ad affermare che rotE
campo elettrico si può scrivere come gradiente di un potenziale V :
~ = −∇V
~
E
~ attraverso
Per il campo magnetico, si verifica facilmente che il flusso di B
una superficie chiusa è sempre nullo (cosa che, in forma locale, si traduce
~ = ∇
~ ·B
~ = 0). Ci si può porre la domanda se anche il campo B
~
in divB
~ lungo una linea chiusa sia
sia conservativo, ovvero se la circuitazione di B
~ = ∇
~ ∧B
~ = 0.
identicamente uguale a zero o, equivalentemente, se rotB
Da proprietà generali dei campi vettoriali ci si rende conto facilmente che
questo non è possibile: infatti, si può dimostrare che la conoscenza simultanea di rotore e divergenza di un campo in ogni punto dello spazio definisce
univocamente il campo vettoriale in questione. Ma un campo costante su
tutto lo spazio ha certamente sia divergenza che rotore nulli, quindi se per
ogni campo magnetico fosse contemporaneamente vero che rotore e divergenza sono nulli in ogni punto dello spazio, allora l’unico campo magnetico
possibile sarebbe quello uniforme in tutto lo spazio, cosa che contrasta con
l’evidenza. E’ quindi evidente che si avrà senz’altro
I
~ · d~` 6= 0
B
C
e rimane aperto il problema di quanto vale la circuitazione di B lungo una
linea chiusa. Esistono molti modi di trovare una risposta a questa domanda.
Quello che viene proposto qui di seguito non è sicuramente il metodo più
diretto, ma è il modo più generale di dimostrare la relazione che si troverà
alla fine.
Il potenziale scalare
Abbiamo visto che le sole forze che ammettono un potenziale sono le forze
conservative. Abbiamo anche visto poc’anzi che il campo magnetico non può
1
essere un campo conservativo. Tuttavia, dimostreremo ora che è possibile
definire localmente un potenziale scalare tale che
~ m
~ = −µ0 ∇φ
B
(1)
(il prefattore µ0 non è rilevante per quello che segue, serve in altri contesti
in cui viene utilizzato il potenziale φm ). Questo potenziale, come vedremo
in seguito, ha delle caratteristiche
molto particolari, che fanno sı̀ che la
H
~ · d~` = 0.
relazione 1 non implichi C B
Per trovare la funzione φm il cui gradiente (cambiato di segno) dà il campo
magnetico considereremo per fissare le idee un circuito rettangolare C. Le
considerazioni che si faranno per questo particolare caso sono in realtà del
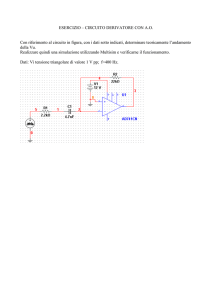
tutto generali, il caso particolare serve solo a fissare graficamente idee. Si
Figure 1: La spira rettangolare usata per fissare le idee. A sinistra,
i lati sono colorati con colori diversi per facilitare la comprensione
del disegno che descrive la spira. A destra, la stessa spira ed il punto
P in cui viene calcolato φm .
consideri quindi il circuito C, disposto in un piano perpendicolare al foglio
(v. fig.1) percorso da una corrente che scorre in verso uscente dal foglio nel
lato superiore e entrante nel foglio nel lato inferiore (nei due lati fuori dal
foglio e paralleli ad esso scorre parallelamente al foglio stesso, dall’alto verso
il basso nel filo ”sopra” al foglio e dal basso verso l’alto nel filo ”sotto” al
foglio), ed un generico punto P nello spazio. Assumendo che φm esista, la
variazione di φm nel passare dal punto P ad un punto distante d~s da P si
può scrivere (per definizione)
~
~ m · d~s = − B · d~s
dφm = gradφm · d~s = ∇φ
µ0
2
~ può essere scritto usando la legge di Lapalace (B
~ =
Ma B
ovvero, sostituendo nella precedente relazione,
dφm
i
=−
4π
I
C
d~` ∧ ~r
r3
µ0 i H d~
`∧~
r
4π C r3 ),
!
· d~s
L’integrazione va eseguita sulle coordinate che definiscono il circuito, mentre
d~s riguarda uno spostamento del punto in cui si calcola il potenziale. Le
coordinate d~` e d~s sono quindi fra loro indipendenti e d~s può essere portato
sotto il segno di integrale:
dφm
i
=−
4π
I
C
I
~ · ~r
(d~` ∧ ~r) · d~s
i
(d~s ∧ d`)
=
−
r3
4π C
r3
dove nell’ultimo passaggio si è fatto uso della proprietà del prodotto misto
(~a ∧ ~b) · ~c = (~c ∧ ~a) · ~b.
Ora, il prodotto vettoriale d~s ∧ d~` è per definizione un vettore che ha come
modulo l’area del parallelogramma che ha come lati d~s e d~`, come direzione
la direzione perpendicolare al suddetto parallelogramma e come verso quello
determinato dalla regola della mano destra: pollice lungo d~s, indice lungo
d~` e medio lungo d~s ∧ d~`. Definendo dA come l’area del parallelogramma
che ha come lati d~s e d~`, e n̂ come il versore perpendicolare al suddetto
parallelogramma, d~s ∧ d~` è quindi equivalente al prodotto n̂dA, anch’ esso
di modulo dA e perpendicolare alla superficie dA, purchè n̂ sia orientato
secondo la regola della mano destra.
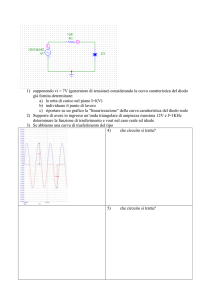
Figure 2: Avvicinare il punto P di una quantità (vettoriale) d~s
equivale ad avvicinare il circuito al punto P di una quantità (vettoriale) −d~s
Per capire meglio cosa rappresenta d~s ∧ d~`, si immagini di ottenere la variazione di φm spostando non il punto di una quantità d~s ma il circuito di una
3
quantità −d~s (v. figura 2). In questo caso il parallelogramma identificato
dai due vettori elementari d~` e d~s è un elemento della superficie ∂Σ che ha
come bordi il circuito prima e dopo lo spostamento (v.figura 3), e quindi
quindi integrare in d~` lungo il circuito C equivale a integrare sulla superficie
∂Σ in d~s ∧ d~` = n̂dA. Ma allora
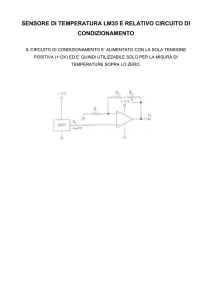
Figure 3: Vettori (elementari e non) coinvolti nel calcolo di dφm . Il
vettore n̂dA è definito dalla relazione n̂dA = d~s ∧ d~`. Si noti che il
vettore disegnato accanto a n̂dA è −d~s e non d~s.
dφm = −
i
4π
I
C
~ · ~r
i
(d~s ∧ d`)
=
3
r
4π
Z
∂Σ
i
n̂ · (−~r)
dA =
3
r
4π
Z
∂Σ
n̂ · (−r̂)
dA
r2
H
Ricordando la definizione di angolo solido (Ω = Σ n̂·r̂
dS, dove ~r è il vettore
r2
che unisce il punto rispetto al quale si calcola l’angolo solido alla superficie
Σ, ovvero nel nostro caso −~r), si ha quindi immediatamente
dφm =
i
dΩ
4π
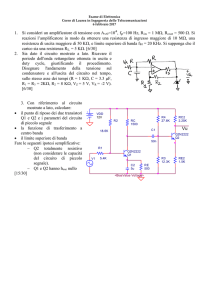
In questa espressione, dΩ rappresenta la variazione dell’angolo solido che
ha come vertice il punto P e come ”apertura” quella determinata dal circuito
C, ovvero la differenza fra l’angolo solido disegnato in grigio scuro in figura
4 e l’angolo solido disegnato in grigio chiaro nella stessa figura.
Dall’ espressione di dφm si passa per integrazione all’espressione di φm :
φm =
i
Ω
4π
(2)
dove Ω è l’angolo solido con cui il circuito C è ”visto” dal punto P . Si noti
che in nessun passaggio utilizzato per derivare l’espressione di φm è stato
4
Figure 4: Variazione dell’angolo solido con cui il circuito C è ”visto”
dal punto P quando quest’ultimo viene spostato di una quantità d~s.
A sinistra, come cambia dΩ se si sposta il circuito di una quantità
−d~s, a destra la stessa variazione ottenuta spostando il punto P .
necessario l’utilizzo di un circuito rettangolare: di fatto, la forma del circuito
è del tutto arbitraria, l’aver studiato il caso particolare del rettangolo ha il
solo scopo di fissare graficamente le idee.
~
Il potenziale cosı̀ ottenuto può essere utilizzato per il calcolo del campo B
Figure 5: Il verso di percorrenza della spira, visto da un generico
punto P nello spazio, cambia se il punto P si trova in punti diversi rispetto alla spira: vista dal punto P , la spira è percorsa dalla
corrente in senso antiorario, ma vista dal punto P 0 la spira risulta
percorsa da corrente in senso orario
in ogni punto dello spazio, tramite la relazione 1. Vanno però fatte alcune
precisazioni. Innanzitutto, abbiamo fatto il conto per un ben determinato
verso di percorrenza della corrente (vista dal punto P , la corrente scorre in
senso antiorario). Se si cambia verso di percorrenza, l’unica cosa che cambia
5
è il verso di d`, e quindi il risultato rimane lo stesso ma cambiato di segno
i
(φm = − 4π
Ω). Lo stesso cambio di segno sarà necessario se ci si sposta nel
semipiano opposto: guardando il circuito da un punto P 0 che si trovi nel
semipiano opposto rispetto a quello considerato, la corrente, se la si vedeva
scorrere in senso antiorario dal punto P , si vedrà scorrere in senso orario (v.
figura 5). Quindi, spostarsi da un semispazio all’altro equivale a cambiare
verso di percorrenza della corrente, e quindi di nuovo a cambiare il segno
nella relazione fra φm e Ω.
Un esempio concreto
Calcoliamo ora il campo magnetico sull’asse di un anello circolare percorso
da corrente utilizzando la definizione di potenziale scalare appena trovata.
Per fare ciò, l’unica cosa da trovare è l’espressione dell’angolo solido ”visto”
dal punto in cui si vuole calcolare il campo. Per ragioni di simmetria, si
può facilmente verificare che il campo sull’asse dell’anello deve essere diretto lungo l’asse stesso e quindi, scegliendo l’asse x coincidente con l’asse
~ = {Bx , 0, 0} e l’equazione 1 implica che le derivate di φm
dell’anello, B
rispetto a y e z devono essere necessariamente nulle. L’unica derivata da
calcolare risulta quindi essere la derivata rispetto ad x. Per ottenerla, è
sufficiente calcolare φm sui punti appartenenti all’asse x, ovvero all’asse
dell’anello. In questo caso, il conto è immediato: infatti, trattandosi di
un anello circolare, l’angolo solido ”visto” dal punto P corrisponde a quello
sotteso ad un cono con un angolo di apertura β (v. figura 6), che si può
dimostrare essere pari a Ω = 2π(1 − cos(β/2)). Indicando con α = β/2, si
ha immediatamente che cos(β/2) = cos
√ α = d/r, dove d = x è la distanza
del punto dal centro dell’anello e r = x2 + R2 è la distanza di un generico
punto dell’anello dal punto in cui si vuole calcolare il campo. Ma allora,
∂Ω
∂
x
R2
√
= −2π
= −2π 2
∂x
∂x x2 + R2
(x + R2 )3/2
ricordando la relazione fra B e gradiente di Ω, si ottiene infine
Bx = −
µ0 i ∂Ω
µ0 i
R2
=
4π ∂x
2 (x2 + R2 )3/2
Se avessimo scelto un punto P 0 a sinistra dell’anello, sarebbe ancora stato
valido Ω = 2π(1 − cos α), ma questa volta cos β = d/r = −x/r e quindi
Ω = 2π(1 + x/r). D’altra parte, come detto in precedenza, cambiando
6
Figure 6: Angolo solido ”visto” dal punto P . Essendo l’anello circolare, l’angolo solido (zona grigia) corrisponde a quello sotteso da
un cono con angolo di apertura β. A destra, la stessa configurazione,
ma con il punto P 0 ”a sinistra” dell’anello.
il semipiano bisogna anche cambiare il segno della relazione fra φm e Ω,
i
ovvero, a sinistra dell’anello, φm = − 4π
Ω e quindi, ancora,
µ0 i ∂
x
µ0 i ∂Ω
=
1+ √
4π ∂x
2 ∂x
x2 + R 2
Bx =
=
µ0 i
R2
2 (x2 + R2 )3/2
Questo risultato è in perfetto accordo con quanto ricavabile direttamente
dalla legge di Ampère-Laplace.
~
La circuitazione di B
Se è vera la relazione 1, è anche immediatamente vera la relazione
I
~ · d~s = −µ0 ∆φm
B
(3)
Γ
dove ∆φm è la variazione complessiva di φm quando si percorre la curva
Γ. Nel caso del campo elettrico e del potenziale V , essendo quest’ultimo
definito univocamente in ogni punto, la variazione complessiva
di V quando
H
~ · d~s = 0.
si percorre una curva chiusa Γ deve essere nulla, e quindi Γ E
Nel caso del campo magnetico, il risultato non è lo stesso a causa di una particolarità della funzione φm . Guardando con maggiore attenzione l’equazione
2, ci si accorge che il potenziale φm può assumere due valori distinti, a causa
del fatto che il circuito C divide il piano in cui giace in due spazi, uno interno al circuito ed uno esterno ad esso. L’angolo solido definito dal circuito
7
può quindi riferirsi o alla superficie interna (figura 7, disegno grigio chiaro)
o alla superficie esterna (figura 7, disegno grigio scuro).
Figure 7: Un singolo circuito definisce due angoli solidi: uno (grigio
chiaro in figura) relativo alla porzione di piano interna al circuito, l’altro
(grigio scuro in figura) relativo alla porzione di piano esterna al circuito.
La somma die due angoli è per definizione l’angolo solido (4π).
I due angoli solidi sono fra loro complementari (la somma dei due angoli
dà l’angolo giro, ovvero 4π), ma per come è stato ricavato φm si può verificare che i due angoli vanno presi con segno opposto: il modo più diretto per
capirlo è considerare che a parità di spostamento d~s se uno dei due angoli solidi aumenta l’altro deve diminuire (la loro somma vale sempre 4π), e quindi
la stessa variazione di φm deve essere associata o all’aumento di uno dei due
i
i
i
dΩ o alla diminuzione dell’ altro: dφm = 4π
dΩ1 = − 4π
dΩ2 = 4π
(−dΩ2 ).
Nel caso finora considerato, l’angolo chiaro va considerato positivo per il
calcolo di φm , l’angolo scuro negativo. Come già osservato, i segni si invertono se si cambia il verso di percorrenza della corrente o se il punto passa
nel semipiano opposto rispetto al circuito (nel nostro caso, se il punto P
~ dal
si trova a sinistra del circuito). D’altra parte, se si vuole ottenere B
gradiente di φm quest’ultimo deve risultare una funzione continua nelle
vicinanze del punto in cui si vuole calcolare il campo (in caso contrario, non
~ m ).
è possibile derivare φm e quindi non è possibile ottenere ∇φ
Facendo riferimento alla figura 8, si considerino due diversi cammini, uno
che va dal punto A al punto B passando all’interno del circuito, ed un altro
che passa dal punto C al punto D passando all’esterno del circuito. Come
appena detto, φm deve risultare continuo in ogni punto del cammino, ed in
particolare nel punto in cui si passa da un semipiano all’altro (ovvero quando
si attraversa il piano su cui giace il circuito). Nel primo caso (segmento AB),
quando si attraversa il piano in cui si trova la spira sia l’angolo positivo che
quello negativo sono prossimi a mezzo angolo giro (ovvero, trattandosi di
angoli solidi, a 2π). Se si vuole preservare la continuità di φm , sarà quindi
8
necessario mantenere in segno di Ω passando da un semispazio all’altro (in
caso contrario, si passerebbe da Ω = 2π a Ω = −2π con una discontinuità
i
∆φm = 4π
4π = i passando attraverso il piano della spira). Nel secondo caso
(tratto CD), l’angolo solido positivo è prossimo a zero avvicinandosi ”da
destra” e prossimo a 4π se ci si avvicina ”da sinistra” (viceversa, l’angolo
negativo è prossimo a −4π, se ci si avvicina ”da destra” e prossimo a zero se
ci si avvicina ”da sinistra”). Per preservare la continuità di φm è necessario
scegliere valori opposti del segno di Ω (positivo a destra, negativo a sinistra):
se si mantenesse il segno positivo, si avrebbe una variazione da zero a 4π nel
passaggio attraverso il piano.
Figure 8: L’attraversamento del piano su cui giace la spira ha conseguenze diverse sul segno di Ω nel caso in cui tale attraversamento
avvenga all’interno o all’esterno del circuito (v. testo). A destra:
l’andamento di Ω man mano che ci si sposta lungo la curva ACDBA.
Se ora si considera l’intero percorso ACDBA, si vede che se si vuole mantenere la continuità di φm lungo tutto il percorso e partendo nel punto A
con un angolo solido positivo (Ω(Ai ) > 0), Ω deve diminuire dal punto A
fino ad annullarsi quando passa per il piano definito dalla spira nel segmento
CD, diventare negativo e continuare a crescere (in modulo) fino al punto B.
Nel segmento BA, il valore di Ω deve quindi essere preso sempre negativo
(zona scura) per preservare la continuità, e quindi continua a crescere (in
modulo) per tutto il tratto BA. Quando si raggiunge nuovamente il punto
A, il valore di Ω risulta necessariamente quello negativo (Ω(Af ) < 0). La
variazione complessiva del potenziale lungo la curva ACDBA vale quindi
∆φm =
i
i
i
(Ωf − Ωi ) =
([Ωi − 4π] − Ωi ) = − 4π = −i
4π
4π
4π
9
Dove si è indicato con Ωi l’angolo solido (da intendersi positivo per il calcolo
i
di φm ) nel punto A all’inizio del percorso ACDBA (φm (Ai ) = 4π
Ωi ), con
Ωf l’angolo solido (da intendersi negativo per il calcolo di φm ) nel punto
i
A alla fine del percorso ACDBA (φm (Af ) = − 4π
Ωf ) e si è usato il fatto
che i due angoli nel punto A sono necessariamente complementari fra loro
(−Ωf + Ωi = 4π ⇒ Ωf = Ωi − 4π). Sostituendo nella 3 si ottiene quindi
I
~ · d~s = µ0 i
B
(4)
Γ
Che è il risultato finale cercato. A riguardo di questa formula, è importante
notare alcune cose:
• il risultato finale è dovuto sostanzialmente al fatto che nell’attraversare
il piano su cui giace la spira l’angolo solido Ω deve variare in modo
differente se l’attraversamento avviene all’interno o all’esterno della
spira se si vuole preservare la continuità di φm . Non ha quindi alcuna
relazione con la forma del circuito C, nè con la forma del percorso Γ
su cui si calcola la circuitazione.
• Se si procede nello stesso modo ”girando attorno” al filo superiore
(con corrente uscente) procedendo sempre in senso orario si otterrebbe
facilmente ∆φm = i, ovvero lo stesso risultato ma cambiato di segno.
La differenza fra i due casi si capisce se si considera la regola della vite
applicata alla curva che si percorre per calcolare la variazione di φm
~ dal momento che stiamo
(o equivalentemente, la circuitazione di B):
percorrendo la curva in senso orario, la regola della vite dice che a
questo verso di percorrenza è associato un vettore entrante nel foglio.
Ora, nel primo caso (la curva che racchiude il filo in basso), il vettore
associato alla curva tramite regola della vite è concorde con il verso
di percorrenza della corrente. Nel secondo caso (la curva racchiude il
filo in alto) i due vettori sono invece discordi. La forma più generale
dell’equazione 4 è quindi
I
~ · d~s = ±µ0 i
B
Γ
dove il segno della corrente va considerato positivo se la corrente concatenata è concorde con il verso che si ottiene con la regola della vite
a partire dal verso di percorrenza della curva Γ, negativo altrimenti.
• se la curva Γ è concatenata con più fili percorsi da corrente, ogni filo
10
~ Complessivamente,
contribuirà al valore finale della circuitazione di B.
I
~ · d~s = µ0
B
X
Γ
±ik
k
dove il segno delle varie ik va scelto come già detto.
• dal momento che per definizione la corrente i rappresenta il flusso del
vettore densità di corrente J~ attraverso la sezione del filo, la sommatoria a destra del segno di integrale si può anche scrivere
X
±ik =
k
Z
~
J~ · dS
Σ
(dove Σ è la superficie aperta che ha come contorno la curva Γ) purchè
la superficie Σ sia orientata secondo la regola della vite a partire dal
verso di percorrenza di Γ. Questo permette di scrivere
I
~ · d~s = µ0
B
Z
~
J~ · dS
Σ
Γ
Con questa formulazione, non sono necessarie ulteriori specifiche
sul
H
~
verso della corrente. Inoltre, usando il teorema di Stokes ( Γ B · d~s =
R
~
~
~
Σ (∇ ∧ B) · dS, dove la relazione fra Γ e Σ è la stessa vista poc’anzi)
si ottiene immediatamente
Z
Σ
~ ∧ B)
~ · dS
~=
(∇
Z
~ · dS
~⇒∇
~ ∧B
~ = µ0 J~
(µ0 J)
Σ
(l’uguaglianza dell’integrando discende dall’uguaglianza degli integrali
a causa del fatto che la superficie Σ è arbitraria), ovvero la quarta
equazione di Maxwell in forma locale.
11