testi d`esame diodo

Diodo
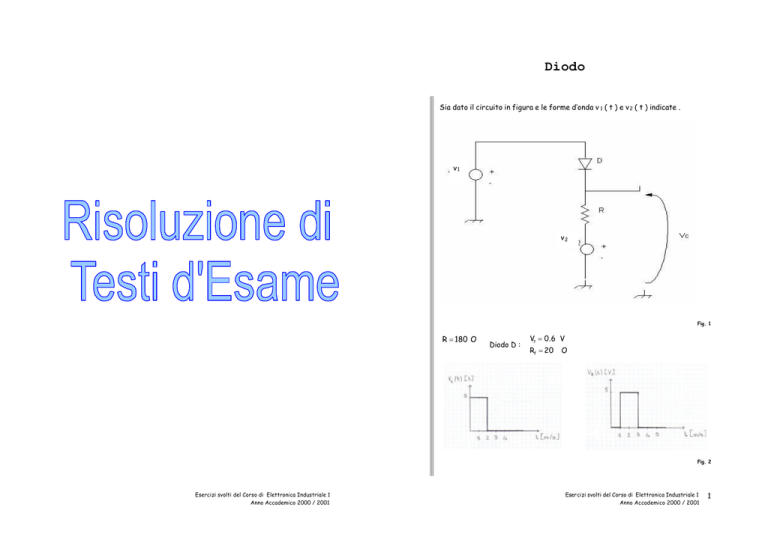
Sia dato il circuito in figura e le forme d’onda v 1 ( t ) e v 2 ( t ) indicate .
v1
v2
Fig. 1
R = 180 O
Diodo D :
V? = 0.6 V
Rf = 20
O
Fig. 2
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
1
Tracciare v 0 ( t ) per 0 ≤ t ≤ 4
ms 1 .
si nota che il diodo lavora in polarizzazione diretta , quindi lo si può sostituire con il
modello ai grandi segnali caratterizzato da un generatore di tensione Vγ con in serie
un resistore.
Si può scrivere la LKT :
v1 (0 ) − v? − (Rf + R) ⋅ I(0 ) = 0 da cui si ottiene :
♦SVOLGIMENTO♦
Si suppone :
⇒ I( 0 ) =
e:
IS = 0
v1 (0 ) − v? 4.4
=
= 0.022 A
Rf + R
200
⇒ v0 (0 ) = R ⋅ I(0 ) = 180 ⋅ 0.022 = 3.96 V
Rr → ∞
z All’istante t=0 si possono dedurre dai grafici della pagina precedente i valori di v1 e
v 2:
v1 (0 ) = 5 V
fino all’istante t=1 in quanto v 1( t ) e v 2 ( t ) restano costanti.
v2 (0 ) = 0 V
z All’istante t=1 i valori di v 1 e v 2 saranno:
v1 (1) = 5 V
v1
v2 (1) = 5 V
γ
f
Fig. 3
1
Fig. 4
Supporre la commutazione del diodo istantanea
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
2
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
3
Si calcola il valore di v1 ( t ) − v2 ( t ) per il quale il diodo passa in polarizzazione inversa
osservando che in tale caso il diodo diventa un aperto e quindi sulla resistenza R non vi
è alcuna caduta di tensione:
LKT :
la differenza tra v 1 e v 2 risulta essere :
v1 (3) − v2 (3) = 0 V < 0.6 V
il diodo è ancora in polarizzazione inversa ma il valore di v0 (3 ) = v2(3 ) = 0 V .
v1 ( t ) − 0.6 − v2( t ) = 0 ⇒ v1 ( t) − v2 ( t) = 0.6 V
il diodo lavora in polarizzazione inversa per :
v1 ( t ) − v2( t ) ≤ 0.6 V
Quando v1 (1) = 5 V e
L’uscita rimane costante a 0 Volt anche per istanti superiori a t = 3 :
v2 (1) = 5 V si ha : v1 ( 1 ) − v2 ( 1 ) = 0 < 0.6 V quindi il diodo
lavora in polarizzazione inversa e si comporta come un circuito aperto .
Sul resistore non vi è alcuna caduta di tensione per cui si avrà :
v0 = v2(1) = 5 V
fino all’istante t = 2.
z All’istante t=2 v 1 e v 2 assumeranno i seguenti valori:
v1 (2) = 0 V e v2(2 ) = 5
V
e la differenza tra v 1 e v 2 risulta essere :
v1 (2) − v2(2) = −5 V < 0.6 V
si può quindi dedurre, per quanto detto in precedenza che il diodo continua a lavorare
in inversa con :
v 0 (2 ) = v2 (2 ) = 5
Fig. … 5
V
z All’istante t = 3 v 1 e v 2 saranno :
v1 (3) = 0 V e v2(3) = 0 V
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
4
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
5
Si chiede di :
Sia dato il seguente circuito :
a) Calcolare l’istante t1 al quale il diodo inizia a condurre
b) Calcolare e disegnare andamento di VOUT (t) nei tre casi :
1) t < t1
L
2) t1 < t < 10− 3 s
3) t > 10-3 s
♦SVOLGIMENTO♦
Anche in questo esercizio :
del diodo .
IS = 0
Rr → ∞
ovvero si suppone istantanea la commutazione
Fig..1
V? = 0.7 V
a) All’istante t = 0 si deduce dal grafico della pagina precedente che vIN (0 ) = 0 V
RL = 10 5 Ω
quindi si può affermare che il diodo lavora in polarizzazione inversa e si comporta
come un aperto.
Il diodo inizierà a condurre quando raggiungerà una differenza di potenziale ai suoi
capi pari a Vγ = 0 . 7 V = v d .
Diodo D : Rf = 50
O
Applicando la LKT al circuito si ottiene:
Con:
L
Fig. 2
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
6
Fig.3
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
7
VIN (t1 ) − 0 .7 = 0
⇒ VIN ( t1 ) = 0. 7 V
2
e utilizzando nuovamente il grafico ( t, V IN(t)) si ottiene :
⇒ t1 = 0.7 ms è l’istante in cui il diodo inizia a condurre .
γ
Fig. 4
VIN (t ) − Vγ − (Rf + RL ) ⋅ i( t) = 0
LKT :
⇒ i( t) =
b) Si analizzano i singoli casi :
1) All’istante t<t1 non sono presenti cadute di tensione su RL e la differenza di
potenziale ai suoi capi è nulla quindi si può dedurre che :
VOUT ( t) = 0 V 3
Fig. 5
VIN (t ) − Vγ
(Rf + RL )
VOUT (t ) = RL ⋅ i( t) = RL ⋅
Quindi :
(V
( t) − Vγ )
Rf + RL
IN
Dato che VIN(t) è una retta , VOUT (t) che dipende direttamente da essa avrà un
andamento lineare.
2) All’istante t1<t<1 la situazione è ben diversa :
z quando t=t1 il diodo comincia a lavorare in polarizzazione diretta ed è quindi
possibile sostituirlo con il modello ai grandi segnali.
Scrivendo la LKT per il circuito:
⇒ per t = t1 VOUT (t1 ) =
⇒ per t = 1 VOUT (t ) =
103
(50 + 103 ) ⋅ (0.7 − 0.7 ) = 0 V
103
(50 + 10 ) ⋅ (1 − 0.7 ) = 0.286 V
3
2
La caduta sul resistore R L è nulla in quanto il diodo è un aperto ed in quanto tale la sua caduta di
tensione è nulla
3
Da sottolineare che l’aumento di V IN(t) fa aumentare solo la differenza di potenziale ai capi del diodo,
infatti si ha che vd (t) = VIN(t).
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
8
z Quando t>1 si avrà il valore di VIN(t) costante e pari a quello ottenuto per t=1, il
diodo continua a lavorare in polarizzazione diretta ed il valore di VOUT(t) è 0.286 V.
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
9
Sia dato il seguente circuito :
v
Fig.6
Fig.1
RS = 10 Ω
VZ = −6 V
IZK = −100 mA
VS = 10
V
Si chiede di
a) determinare la retta di carico ed il punto di lavoro graficamente.
b) determinare la minima resistenza di carico RL tale che i>IZK quando v = VZ .
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
10
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
11
♦SVOLGIMENTO♦
a) Si calcola il circuito equivalente di Thevenin visto ai capi del diodo :
v
Fig.3
Applicando la LKT al nuovo circuito si può determinare il valore di V :
Fig.2
ETH + RTH ⋅ i + V = 0
⇒ V = −RTH ⋅ i − ETH
Da cui si ottiene il valore di E TH:
ETH =
quindi :
RL
10 ⋅ RL
⋅V =
RS + RL S 10 + RL
V=−
e RTH :
RTH =
RL ⋅ RS
10 ⋅ RL
=
RL + RS 10 + RL
10 ⋅ RL
10 ⋅ RL
⋅i−
10 + RL
10 + RL
(♣ )
è l’equazione della retta di carico 4 :
il circuito diventa :
4
Si può disegnare determinando le sue intersezioni con gli assi :
asse X : si pone i = 0 e si ottiene
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
12
V=−
10 ⋅ RL
10 + RL
asse Y : si pone v = 0 e si ha : i = 1 A
anche se il valore di RL non è noto.
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
13
Sia dato il circuito:
Fig.4
Fig.1
Il punto di lavoro è il punto A.
b) Dall’equazione (♣ ) si può determinare il valore di i:

10RL   10 + RL
⋅
i =  − V −
10
+ RL   10 ⋅ RL

 60 + 6 ⋅ RL − 10 ⋅ RL 60 − 4 ⋅ RL
=
=

10 ⋅ RL
10 ⋅ R L

R = 1 KΩ
R1 = R 3 = 2 KΩ
Diodi D1,D2,D3 identici:
Vγ = 0 . 7 V
Rf = 0
Rr → ∞
si impone : i<IZK
e si ottiene :
60 − 4 ⋅ RL
10 ⋅ RL
Si chiede di calcolare 5 :
< −100 ⋅ 10 − 3
a) Le correnti nei diodi D1,D2,D3
b) La tensione del nodo a
⇒ 60 − 4 ⋅ R L < −RL
⇒ R L > 20
Ω
si può quindi affermare che la minima resistenza di carico sarà : (RL )MIN = 20 Ω
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
5
14
Supponendo inizialmente tutti e tre i diodi in conduzione
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
15
Dall’equazione (3) è possibile determinare il valore assunto dalla corrente I:
♦SVOLGIMENTO♦
a) Si indicano nel circuito i versi delle correnti:
I=
16 − 0.7
= 15.3 mA
1 ⋅ 103
sostituendo questo valore di I nell’equazione (2) si ottiene I 1 :
10 = 1 ⋅ 103 ⋅ 15. 3 ⋅ 10 −3 + 0 . 7 + (2 ⋅ 103 ) ⋅ I1 + 1
⇒ I1 =
10 − (15 .3 + 0 . 7 + 1)
= −3. 5 mA
2 ⋅ 103
dall’equazione (4) è possibile ora determinare il valore di I3:
10 = (1 ⋅ 10 3 ⋅ 15 .3 ⋅ 10 −3 ) + 0. 7 + 2 ⋅ 103 ⋅ I3 − 8
⇒ I3 =
(10 − 15 .3 − 0. 7 + 8)
= 1 mA
2 ⋅ 10 3
infine dall’equazione (1) si ricava I2 :
Fig.2
15. 3 ⋅ 10− 3 = 3. 5 ⋅ 10 −3 + 1 ⋅ 10 − 3 + I2
⇒ I2 = (15. 3 − 3 .5 − 1) ⋅ 10 −3 = 10. 8 mA
Si ipotizza che i tre diodi identici lavorino in polarizzazione diretta così da poterli
approssimare con un generatore di tensione pari a Vγ .
Si inseriscono in un unico sistema di equazi oni la LKC applicata al nodo a e le LKT
ricavabili dal circuito così da ottenere:
I = I1 + I2 + I3
10 = R ⋅ I + V? + R1 ⋅ I1 + 1
10 = R ⋅ I + V? − 6
10 = R ⋅ I + V? + R3 ⋅ I3 − 8
(1)
(2 )
(3 )
(4 )
da notare che le correnti I2 ed I3 trovate sono positive , questo significa che il verso
assegnato loro nella figura 2 era corretto quindi i diodi D2 e D3 soddisfano l’ipotesi di
partenza e lavorano effettivamente in polarizzazione diretta. Mentre la corrente I1
risulta negativa per cui si può affermare che il diodo D1 lavora in polarizzazione
inversa .
I diodi in esame devono, per quanto appena rilevato, essere approssimati nel modo
seguente:
Diodo D1 → circuito aperto
Diodo D2 → generatore di tensione Vγ
Diodo D3 → generatore di tensione Vγ
con Vγ=0.7 V, R=1 K Ω e R2=R 3= 2 KΩ.
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
16
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
17
Fig.3
Il circuito diventa quello rappresentato in fig.3 ed i valori delle correnti :
I:
I3:
I1:
I2:
da equazione (3) sarà ancora I= 15.3 mA
da equazione (4) sarà ancora I3= 1 mA
dato che al posto del diodo si inserisce un circuito aperto diverrà I1=0
da equazione (1) diverrà I1 = 14.3 mA
b) La tensione al nodo a si può determinare, note tutte le correnti del circuito
applicando nuovamente la LKT:
LKT: VA = 10 − R ⋅ I = 10 − (1 ⋅ 103 ⋅ 15. 3 ⋅ 10− 3 ) = −5. 3 V
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
18
Si chiede:
Transistori
a) Di dimostrare che il transistore è polarizzato in ZAD1
b) Di calcolare valori di αF e αR
Sia dato il seguente circuito:
c) di dettagliare il circuito equivalente di “Ebers – Moll ” in queste condizioni di
polarizzazione e di semplificarlo opportunamente 2
♦SVOLGIMENTO♦
E
Facendo riferimento alla figura seguente:
?
Fig.1
E
Ove:
VCC = 9 V
βF = 50
E
VEE = −9 V
βR = 1
RE = 8.2 KΩ
VBE = 0. 7 V i n ZAD
Fig.2
1
2
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
28
Si calcolino i valori di IE, IB, VCE , IC , VBC.
Si considerino IC S ed IES dell’ordine di 10 - 9 A
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
29
a) Si supponga che il transistore lavori in ZAD :
quindi si avrà
VBE = 0 .7
V
3
e
β = 50
IB =
4
IC 0 .992 ⋅ 10 −3
=
= 0. 01984 mA
β
50
per determinare il valore delle tensioni VcE
applicando la LKT al circuito in esame si ottiene :
e VBC si può utilizzare ancora una volta la
LKT applicata alla parte di destra del circuito:
LKT :
VEE + RE ⋅ IE + VBE = 0
LKT :
sostituendo i corrispondenti valori numerici è possibile determinare la corrente
nell’emettitore indicata con IE :
VEE + RE ⋅ IE + VCE − VCC = 0
che in termini numerici diventa:
− 9 + 8 .2 ⋅ 103 ⋅ 1. 0122 ⋅ 10−3 + VCE − 9 = 0
− 9 + 8. 2 ⋅ 10 3 ⋅ IE + 0 .7 = 0
⇒ IE =
9 − 0. 7
= 1. 0122 ⋅ 10− 3 A
8 . 2 ⋅ 103
ricordando ora il legame che permette di determinare il guadagno diretto di corrente
di cortocircuito α5 noto il valore di β si può scrivere:
α
1 −α
β
50
⇒α =
=
= 0. 98
1+ β
51
β=
il valore di VCE sarà :
VCE = 18 − 8.3 = 9.7 V
mentre si può determinare il valore della tensione VBC scrivendo:
VBC = −VCE + VBE = −9. 7 + 0. 7 = −9 V
ricavato il valore di α è possibile determinare la corrente nel collettore, indicata con
IC :
a questo punto occorre ricordare che :
IC = α ⋅ IE = 0 .98 ⋅ 1 .0122 ⋅ 10 − 3 = 0. 992 mA
la giunzione BC lavora in diretta se VBC < 0 V
la giunzione CE lavora in diretta se VCE ≥ 0.3 V 6
ma noto il valore di β è anche possibile determinare la corrente di base, indicata con
IB :
⇒ quindi si è accertato che il transistore lavora effettivamente in ZAD.
3
Con questa ipotesi affermiamo che la giunzione BE lavora in diretta; se lavorasse in inversa si
potrebbe scrivere VBE ≅0.
4
α e β indicano entrambi dei guadagni in corrente ma a seconda del pedice che li accompagna fanno
riferimento a situazioni diverse:
βF indica il guada gno diretto di corrente di cortocircuito tra collettore e base, di solito βF ≥ 100
βR indica il guadagno inverso di corrente di cortocircuito tra emettitore e base, di solito βR ≅ 1
α F indica il guadagno diretto di corrente in cortocircuito tra l’emettito re ed il collettore, di solito si ha
b) Per calcolare il valore dei due guadagni α F ed α R si può ricordare la già citata
relazione che li lega ai guadagni β F e β R :
0.99 ≤ αF ≤ 1
α R indica il guadagno inverso di corrente di cortocircuito tra emettitore e collettore, di solito
0 . 4 ≤ αR ≤ 0 .8
⇒ in questo caso si userà il valore di βF e si determinerà il valore di α F
5
Che ovviamente è uguale ad αF
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
6
30
In realtà si dovrebbe considerare anche la giunzione BE che lavora in diretta quando VBE ≅ 0.6 ÷ 0.7
ma è stata posta come ipotesi di partenza V BE = 0.7 V
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
31
⇒ αF =
βF
50
=
= 0 .98
1 + β F 51
αR =
βR
1
= = 0. 5
1 + βR 2
VBE = 0.7 V
c) E’ possibile ora dettagliare il circuito equivalente ai grandi segnali conosciuto anche
come circuito equivalente di “ E bers – Moll” che comprende due generatori pilotati
CCCS7 ( in cui il verso della corrente è contrario a quello della corrispondente
giunzione):
IF
La corrente nella giunzione BC sarà:
IR ≅ −ICS
quindi dato che si è dimostrato che il transistore lavora in ZAD e che la V BC <<0 il
diodo di destra diventa un circuito aperto ed il generatore pilotato di sinistra
sparisce.
Osservazione:
è possibile sostituire all’unico diodo rimasto il suo modello
equivalente ai grandi segnali considerando però RF ≅ 0 cosicché il
modello sia rappresentato soltanto da un generatore di tensione Vγ =
VBE = 0.7 V
α
C
Fig.38
In particolare si può scegliere di lavorare “a base comune “ ovvero di esprimere le
variabili presenti nel modello in funzione delle tensioni VBE e VBC rispetto alla base:
 VBE

 V

IF = IES ⋅  e T − 1 




nella giunzioneBE
 VBC

IR = ICS ⋅  e VT − 1




nella giunzioneBC
α
ricordando i valori ottenuti per VBC e VBE :
VBC = - 9 V ⇒ VBC << 0
7
I generatori pilotati sono anche detti generatori dipendenti o generatori controllati e sono
componenti a quattro terminali utilizzati per modellizzare il comportamento dei transistori.
Sono spesso indicati con diverse sigle in questo caso CCCS significa “ Current Controlled Current
Source” e la loro equazione caratteristica mostra una diretta proporzionalità tra la corrente generata
e la corrente che scorre in un altro ramo del circuito.
8
La figura comprende già le considerazioni fatte in seguito
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
32
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
33
Sia dato il circuito:
♦SVOLGIMENTO♦
a) Si rappresenta il “circuito di polarizzazione “ ricordando che alle basse frequenze
è possibile approssimare le capacità con circuiti aperti:
Fig.1
Fig.2
VCC = 10 V
IC0 = 1 mA
VBE0 = 0.7 V
VC0 = 5 V
Se il transistore è polarizzato in ZAD si può affermare che la corrente nella base è
legata alla corrente nel collettore mediante il guadagno diretto di corrente di
cortocircuito tra collettore e base 9 :
ß = 100
IC = ß ⋅ IB
⇒ IB =
Si chiede di determinare :
IC
ß
=
1 ⋅ 10 − 3
= 10 µA
100
a) I valori di RB ed RC tali che il transistore sia polarizzato in ZAD
dalla LKT applicata al circuito in esame si ricava :
b) I parametri del circuito ai piccoli segnali del transistore
LKT: 10 − VBE − RB ⋅ IB = 0
c) Il guadagno ai piccoli segnali ed in bassa frequenza
Inoltre si avrà che:
⇒ RB =
10 − 0.7
= 930 KΩ
10− 5
9
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
34
Qui lo si indica solo con β in quanto si considera che il diodo lavori in ZAD in realtà può essere inserito
anche come βF
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
35
VC0 = RC ⋅ I C0
⇒ RC =
VC0
5
=
= 5 KΩ
IC0 1 ⋅ 10 −3
Fig.3
b) Si determinano ora i parametri caratteristici del circuito equivalente ai piccoli
segnali del transistore:
Y La “ transconduttanza “ , indicata solitamente come g m , dipende dal punto di lavoro
e può essere calcolata come:
gm =
Dal nuovo modello , in cui si è inserito al posto di un generatore di corrente pilotato in
tensione VCCS10 un generatore di corrente pilotato in corrente CCCS risulta:
rπ = hie 11= 2.5 K Ω
e
ß = hfe
12
=100
dove hfe rappresenta nel modello ad emettitore comune il “guadagno di corrente ai
piccoli segnali “.
IC0
VT
assumendo VT pari a 25 mV a temperatura ambiente, il valore di g m sarà :
iB =
10 −3
gm =
= 0.04 O -1
25 ⋅ 10 −3
Y La “ resistenza base – emettitore” , indicata con rπ ,rappresenta la resistenza
differenziale della giunzione base – emettitore e si può calcolare come:
rp =
ricordando che iB ( t) =
VOUT = − R C ⋅ h fe ⋅
Vs
= 140
h ie
V
c) Infine si può calcolare il valore del guadagno di tensione ai piccoli segnali, indicato
vBE (t )
con AV:
iB ( t)
IC0
si avrà:
ß ⋅ VT
rp =
VS
0.7
=
= 0.28 mA
hie 2.5 ⋅ 103
considerando che :
ß ⋅ VT
ß
100
=
=
= 2.5 KO
IC0
gm 0.04
iB =
VS
hie
VOUT = − R C ⋅ h fe ⋅
Il circuito equivalente ai piccoli segnali risulta il seguente:
Vs
h ie
quindi
10
“Voltage Controlled Current Source” per cui l’espressione caratteristica è i(t)=G ⋅v(t) ovvero la
corrente generata è proporzionale alla tensione in qualunque altro punto del circuito
11
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
36
In realtà si dovrebbe sommare ad
rπ anche una componente indicata con rb ,cioè la “resistenza della
zona di base “ ma dato che rb è di un ordine di grandezza più basso rispetto ad rπ la si può anche
trascurare
12
Le due quantità, β ed hfe, sono concettualmente differenti ma si può dimostrare che sono
quantitativamente uguali
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
37
AV =
h
VOUT
100
= −RC ⋅ fe = −5 ⋅ 103 ⋅
= −200
VS
hie
2.5 ⋅ 1000
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
38
♦SVOLGIMENTO♦
Funzioni di trasferimento
Risulta utile passare al circuito con le impedenze dove
1
Z (S ) = R2 +
:
SC
Sia dato il seguente circuito:
ZR (S) = R1 = 99 ⋅ 103 Ω e
Fig.2
Utilizzando la formula del partitore di tensione si può determinare il valore di V OUT (S)
in funzione di VIN(S):
Fig.1
C = 10- 9 F
R1 = 99 ⋅ 103 Ω
R2 = 103
Ω
T (S ) =
VOUT (S )
VIN (S )
ZR (S ) + Z (S )
⋅ VIN (S ) =
R2 +
1
SC
R1 + R2 +
1
SC
⋅ VIN (S )
VOUT (S )
VIN (S)
=
R2 +
1
SC
1
R1 + R2 +
SC
=
R2 ⋅ SC + 1
(R2 + R1 ) ⋅ SC + 1
ponendo ora S = jw è possibile determinare l’espressione della risposta in frequenza
T(jw):
e si disegni il diagramma di Bode del modulo e della fase di T(S).
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
Z (S)
sostituendo ora questo valore di VOUT all’interno della funzione di trasferimento si
ottiene:
Si calcoli la funzione di trasferimento :
T (S ) =
VOUT (S) =
19
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
20
T ( jw ) =
R2 +
Il segnale globale sarà1 :
1
jwC
1
R1 + R2 +
jwC
si determinano i valori di zeri e poli, riscrivendo la T(jw) nella forma:
1
jw ⋅ 10− 9
10− 6 ⋅ jw + 1
T (jw ) =
= −4
1
10 ⋅ jw + 1
100 ⋅ 103 +
jw ⋅ 10−9
103 +
lo zero risulta essere:
z = − 106
rad/sec
⇒ z = 106 rad/sec
ed il polo :
p = −104
rad/sec
⇒ p = 104 rad/sec
Fig.4
4
4
Il diagramma di Bode per il modulo sarà dato dalla somma di tre contributi:
Il diagramma di Bode relativo alla fase, analogamente a quanto già detto per il
modulo sarà:
Fig.5
Fig.3
1
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
21
Si deduce che è un filtro passivo di tipo passa basso e non un amplificatore
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
22
La somma fornisce un segnale globale del tipo:
Data la seguente funzione di trasferimento :
T (S ) = 103 ⋅
s + 10
s + 1000
si determini il corrispondente diagramma di Bode in modulo e fase e si indichi il
tipo di filtro.
Fig.6
♦SVOLGIMENTO♦
E’ possibile riscrivere la funzione di trasferimento nella forma:
s
10 ⋅ 1 +


10
 = 10 ⋅
T (S ) = 10 ⋅
s
3 

10 ⋅  1 +


100 
3
1 + s 



10 
s
1 +




1000 
lo zero sarà :
z = −10
rad/sec ⇒ z = 10
rad/sec
il polo sarà:
p = −1000 rad/sec
⇒ p = 1000
rad/sec
il guadagno è K = 10.
4
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
23
Il diagramma del modulo è dato da tre contributi, la retta orizzontale rappresenta
la componente costante a 20 ⋅ log10 10 = 20 dB :
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
24
Fig.3
Fig.1
La somma sarà:
Il segnale globale sarà:
Fig.4
Fig.2
4
2
Il diagramma della fase è dato anch’esso da tre contributi 2:
All’interno di questi tre contributi uno è identicamente nullo: la fase di K
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
25
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
26
Si tratta di un filtro attivo 3 di tipo “ Passa Alto” :
Fig.5
3
Cioè amplificatore in quanto il guadagno K non è unitario
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
27
Il secondo passo è quello di ricavare la sintesi del FF JK.
Esercizi di digitale
E’ data la tabella di verità di un FF di tipo AB:
A
0
1
0
1
B
0
0
1
1
j
0
0
1
1
Q(n+1)
Q (n )
Q(n)
1
0
Costruire questo FF facendo uso di un FF di tipo JK e della logica addizionale
necessaria.
k
0
1
0
1
Q(j+1)
Q(j)
0
1
Q (j)
j k
Q(n)
0
1
00
0
1
01
0
0
11
1
0
Q (n + 1) = Q (n )j + Q(n)k
=>
10
1
1
(2)
Effettuando ora il confronto tra la (1) e la (2) si può affermare che:
A=j
k = AB => k = AB = A + B
(per il teorema di De Morgan)
Si ottiene quindi
♦SVOLGIMENTO ♦
Q (n + 1) = AQ(n ) + ABQ(n) + AB = Q'(n + 1) + AB
Il primo passo da eseguire è quello di effettuare la sintesi del flip-flop AB
mediante l’utilizzo della seguente mappa di Karnaugh ricavata dalla tabella di verità
fornita:
A B
Q(n)
0
1
00
1
0
01
1
1
11
0
0
10
0
1
uscita FF JK
… a cui corrisponde il seguente circuito logico:
A
J
B
K
Q’(n+1)
Q(n+1)
Q'(n + 1 )
AB
… da cui si ricava:
Q (n + 1) = Q(n)A + Q(n )AB + AB
(1)
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
39
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
40
Sia data la seguente funzione logica:
La sintesi minima di F risulta così essere:
F = ac + bc + abd + acd
F = abc + (a + b + d)(ab d + c)
c) La mappa di F si ricava banalmente dalla mappa precedente …
Si desidera che:
a) Si sviluppino i prodotti semplificando il più possibile.
b) Si ricavi la mappa di Karnaugh dalla funzione così semplificata.
c) Dalla mappa ottenuta si ricavi dalla funzione F e la si sintetizzi.
ab
c d
♦SVOLGIMENTO ♦
a) F = abc + (a + b + d)(abd + c ) = abc + aabd + abd + abdd + a c + bc + dc =
00
01
00
0
0
01
0
0
11
0
0
10
1
0
11
1
10
1
1
1
0
1
0
0
… da cui si ricava
= abc + abd + a c + bc + dc
F = ac + bcd + a bcd
b) Le componenti logiche di F sono così interpretate …
abc → 101 abd → 11 - 0
ac → 0 - 0 bc → - 10 dc → - -01
… da cui si ottiene la seguente Mappa di Karnaugh
ab
c d
00
01
00
1
1
01
1
1
11
1
1
10
0
1
11
0
0
0
1
10
0
0
1
1
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
41
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
42
Si progetti, usando il metodo ASM, una macchina a stati finiti per la generazione
di un CK a due fasi φ1 e φ 2 come quello mostrato in figura.
Il diagramma ASM che esplica il comportamento desiderato è il seguente:
φ1 = 1
φ2 = 1
Clock
φ1
0
φ2
(a)
EN
1
φ1 = 0
φ2 = 1
Fig. .1
Le due fasi, φ! e φ2, sono segnali periodici il cui periodo è pari a quattro volte il CK
di sistema (segnale Clock in figura).
La macchina dispone di un ingresso EN che, quando è a 1, abilita il funzionamento
sopra descritto e, quando è a 0, mantiene costante l’ultimo valore assunto dalle
due fasi.
Si richiede:
0
EN
0
EN
1
φ1 = 1
φ2 = 1
a) Il diagramma ASM.
b) La sintesi della macchina a stati finiti.
0
(d)
φ1 = 1
φ2 = 0
(c)
1
EN
Fig. .3
b) Utilizzando il diagramma della ASM appena ricavato, si può ottenere la seguente
♦SVOLGIMENTO ♦
tabella della FSM:
a) La FSM desiderata è mostrata in fig. .2
EN
(b)
EN
0
1
0
1
0
1
0
1
φ1
FSM
CK
φ2
Fig. .2
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
43
SP
(a)
(a)
(b)
(b)
(c)
(c)
(d)
(d)
S1
0
0
0
0
1
1
1
1
S0
0
0
1
1
1
1
0
0
φ1
1
1
0
0
1
1
1
1
φ2
1
1
1
1
1
1
0
0
SF
(a)
(b)
(b)
(c)
(c)
(d)
(d)
(a)
S 1’
0
0
0
1
1
1
1
0
S 0’
0
1
1
1
1
0
0
0
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
44
La struttura della FSM è la seguente:
Per k1:
S1 S0
2
EN
D
4
RC1
1
EN
S1
4
S0
RC2
2
φ1
φ2
00
01
11
10
-
-
0
0
0
1
0
1
CK
CK
Fig. .4
4
•
⇒ k1 = S0 + EN .
Sintesi di un’uscita ( ad esempio φ ! )
S1 S0
EN
0
1
00
1
1
01
0
0
11
1
1
10
1
1
da cui si ricava:
Φ 1 = S1 + S0
•
Sintesi di uno stato (ad esempio S1’). Supponendo di voler utilizzare un FF di
tipo JK, usando la tabella di eccitazione già più volte vista, si ottiene:
Per j1 :
S1 S0
EN
0
1
00
0
0
01
0
1
11
-
10
-
⇒ j1 = S0 + EN .
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
45
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
46
Sono dati i seguenti tre segnali:
(a)
CK
(d)
OUT = 0
OUT = 0
0
0
IN
IN
IN
1
1
OUT = 1
OUT
(b)
(c)
OUT = 1
Fig. .1
Fig. .3
Progettare la FSM che, dato il segnale di polarizzazione di sistema CK e l’ingresso
asincrono IN; genera il segnale OUT.
Si noti che:
•
•
Il segnale OUT va ad 1 per un periodo di CK quando IN ha una transizione
0 à 1 oppure 1 à 0;
La frequenza di In è molto minore di quella di CK.
Dal diagramma ASM si ricava la seguente tabella:
IN
0
1
0
1
-
SP
(a)
(a)
(b)
(c)
(c)
(d)
S1
0
0
0
1
1
1
S0
0
0
1
0
0
1
OUT
0
0
1
0
0
1
SF
(a)
(b)
(c)
(d)
(c)
(a)
S 1’
0
0
1
1
1
0
S 0’
0
1
0
1
0
0
♦SVOLGIMENTO ♦
Utilizzando Flip Flop JK, la struttura della FSM è:
La FSM desiderata e il diagramma ASM che esplica il suo comportamento sono
mostrati, rispettivamente, in fig. .2 e .3:
IN
IN
FSM
D
1
OUT
2
4
RC1
S!
S0
4
RC2
1
OUT
CK
CK
CK
4
Fig. .2
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
47
Fig. .4
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
48
•
Sintesi dell’uscita
In modo analogo per S 2’ occorre sintetizzare j2 e k2.
S1 S0
IN
00
0
0
0
1
•
01
1
1
11
1
1
10
0
0
j0
⇒ OUT = S 0
S1 S0
IN
0
1
00
0
1
01
-
11
-
10
1
0
00
01
11
10
-
1
1
1
1
-
⇒ j0 = S1 ⋅ IN + S1 ⋅ IN
Sintesi delle variabili di stato.
k0
Per lo stato S1’ occorre sintetizzare j1 e k1. Facendo riferimento alla tabella di
eccitazione già più volte vista, si ottiene:
j1
0
1
⇒ k 0 = S0
S1 S0
IN
0
1
k1
S1 S0
IN
00
0
0
01
1
1
11
-
10
-
00
-
01
-
11
1
1
10
0
0
⇒ j1 = S 0
S1 S0
IN
0
1
⇒ k1 = S 0
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
49
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
50
Si descriva, mediante il diagramma ASM, il funzionamento di un FF “edge –
triggered” di tipo JK. Una volta disegnato il diagramma, si sintetizzi la
corrispondente FSM utilizzando un FF di tipo RS. Si richiede quindi:
1)
2)
3)
4)
5)
Q=0
Diagramma ASM del FF di tipo JK;
Tabella della FSM corrispondente;
Tabella di eccitazione del FF RS;
Disegno della struttura della FSM;
Sintesi dello stato.
0
(a)
j
1
(b)
Q=1
0
j
1
0
0
k
1
k
1
♦SVOLGIMENTO ♦
1) Ricordando che un FF di tipo JK si comporta nella maniera descritta dalla seguente
tabella di verità:
j
0
0
1
1
k
0
1
0
1
Q(j+1)
Q(j)
0
1
j
k
FSM
Fig .2
2) Utilizzando il diagramma della ASM appena ricavato, si può ottenere la seguente
tabella della FSM:
Q
Q (j)
Fig. .1
j
0
1
0
0
1
1
k
0
1
0
1
SP
(a)
(a)
(b)
(b)
(b)
(b)
S
0
0
1
1
1
1
Q
0
0
1
1
1
1
SF
(a)
(b)
(b)
(a)
(b)
(b)
S’
0
1
1
0
1
0
… il diagramma ASM è il seguente:
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
51
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
52
Osservazione: per come è stata scelta la codifica, la sintesi dell’uscita è
Q = S.
3) Dalla conoscenza della tabella di verità dei flip–flop SR, si può ricavare la seguente
tabella di eccitazione.
S
0
0
1
1
R
0
1
0
1
Q(k+1)
Q(k)
0
1
-
Tabella di eccitazione
Q(k)
0
0
1
1
Q(k+1)
0
1
0
1
S
0
1
-
5) Infine, si passa ad effettuare la sintesi dello sta to …
j k
R
1
0
ST
0
1
00
0
-
01
0
-
11
1
-
10
1
-
00
0
01
1
11
1
10
0
j k
ST
4) La struttura della FSM è la seguente:
0
1
1
RC2
j
Q
… la quale porta ad ottenere S = j e R = k.
2
CK
k
RC1
2
2
SP
CK
2
ST
SF
CK
Fig .3
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
53
Esercizi svolti del Corso di Elettronica Industriale 1
Anno Accademico 2000 / 2001
54
DGT1 Punti[12/30]
Prova Scritta del 13/12/01
AN1 Punti[11/30]
Dato il seguente circuito:
V CC=5 V
I 0E = 1020 ? A
I1
R1
CB
VIN
IB
I2
R2
V 0BE= 0.7 V
IC
RC
CC
IE
RE
V 0B = 2.7 V
VCC
αF =0.98
R L =1000 Ω
R c = 1000.4 Ω
RL
VOUT
Rb ≅ 0
R 2 = 27000 Ω
V in(t) = 0.025 V
Si chiede di calcolare:
1. Il valore di β f
2. il valore di correnti e tensioni del circuito nel punto di lavoro
3. il valore dei parametri del circuito equivalente del transistore ai piccoli segnali nel punto di
lavoro trovato
4. il guadagno di tensione ai piccoli segnali.
Si progetti una FSM sincrona con un ingresso IN e quattro uscite: ZERO, UNO, DUE, TRE. Normalmente le
quattro uscite sono 0.
Quando il segnale IN permane per due periodi consecutivi di CK ad 1, la FSM decodifica il numero binario
rappresentato dai valori di IN nei due successivi periodi di CK nel modo rappresentato dagli andamenti
temporali in figura. Dopo di che la FSM ritorna in attesa di due periodi consecutivi di CK in cui IN permane
ad 1.
Si progetti la FSM utilizzando la struttura di Mealy. Si chiede di:
1. disegnare il diagramma ASM
2. scrivere la tabella della FSM
3. disegnare la struttura della FSM
4. sintetizzare almeno una uscita ed una variabile di stato (utilizzare FF di tipo JK “edge
sensitive” esintesi di tipo NOR -NOR).
CK
IN
00
ZERO
IN
10
UNO
IN
01
DUE
IN
TRE
11
DGT2 Punti[3/30]
AN2 Punti[4/30]
Siano dati il seguente circuito e l’andamento temporale di V IN(t) specificato di seguito. Si chiede di calcolare
e andamento temporale di VOUT (t) nell’intervallo: ms ≤ t ≤ 4 ms. Si consideri la commutazione del diodo
istantanea ed i seguenti valori del modello ai grandi segnali: Vγ =0,6 V, Rf = 0 Ω, IS = 0 A, R r ≅ ∞ Ω . Si
determino i valori di R 1 = ed R 2 in modo tale che quando V in la corrente I circol ante nella maglia sia pari a
10-2 A.
R1
I
V IN(t)
R2
V 0(t)
[V]
8
6
4
2
Siano dati la rete logica e gli andamenti temporali rappresentati in Figura. Si chieda di disegnare l’andamneto
temporale corrispondente alla variabile di uscita X. (Si suppongano nulle i tempi di propagazio ne delle porte
logiche).
A
B
1 2 3 4 5 t[ms]
Attraverso la KCL applicata al nodo B otteniamoI1:
Svolgimento AN1
Vcc=5V
V BE =0.7V
IE = 1020µA
V B =2.7V
αf =0.98
RC =1.004kΩ
RL = 1kΩ
Rb = 0
R2 = 27kΩ
VT =25mV
I1 = IB+I2 = 0.1+0.02mA =0.12mA
E quindi calcoliamo la resistenza R1 attravero la KVL:
R1 =
1)Calcolare β f
αf
0.98
βf =
=
= 50
1 −α f
0.02
IC Rc − VBC 1V -(-1.3V)
=
= 19167Ω
I1
0.12 mA
2) per calcolare il guadagno in centro banda dobbiamo prima disegnare il circuito equivalente ai
piccoli segnali
Poi calcoliamo VE avendo VB e VBE
V E = V B – VBE = 2.7V -0.7V= 2V
Poi calcoliamo le correnti IB ed I C .
IB =
IE
1 0 2 0µ A
=
= 0 .02 m A
50
βf + 1
IC =I E- IB = 1 mA
Calcolo le resistenze:
VE = IE RE
e quindi la resistenza R E =
VE
=1960Ω
IE
e calcolare i parametri ai piccoli segnali, ovvero h i e e hfe .
Avendo VB ed R 2 possiamo calcolare I2 attraverso la KVL:
rπ=
I2 R2 = VB
Da cui consegue che
I2=
VB 2.7V
=
= 01
. mA
R2 27kΩ
Avendo IC, R C e V E calcoliamo VCE e VBC:
h ie = rπ + Rb =1250Ω
mentre hfe = βf =50 ma solo numericamente.
Applichiamo ora la KVL al circuito ai piccoli segnali per trovare V out e V in ed il loro rapporto AV che
rappresenta il guadagno di tensione in centro banda.
La Vout sarà data da:
V out = hfe ib (RC //RL )
V CE=V CC-ICR C-V E =5V-(1000.4Ω∗1mA)-2V = 2V
V BC = V BE-V CE = 0.7V -2V = -1.3V
VT
25mV
=
= 1250Ω
I B 0 ,02 mA
mentre :
V in= i b hie + (ib + hfe i b ) R E
Svolgimento AN2
Da cui ricaviamo i b in funzione di Vi n:
Per prima cosa bisogna ridisegnare il circuito nel modello ai grandi segnali del diodo:
ib
=
(
Vin
)
h ie + 1+ h fe R E
Sostituendo poi in V out troviamo che :
V out= −
Vin
hie + (1 + hfe ) RE
hfe (R L / /RC)
E quindi Av sarà uguale a:
AV =
Vout
h (R / /RC)
= − fe L
Vin
hie + (1 + hf e ) RE
La KVL del circuito in figura è:
V1 (t ) − Vγ − IR f − IR = 0
Il parallelo tra RC ed RL vale:
RCRL
1000.4 ⋅ 1000
=
= 499.2 Ω
RC + RL
2000.4
Il nostro diodo è in diretta quando:
I=
ma dato che
hie << (1+ hfe ) e che h fe ˜ (1+ hfe )
Vin ( t ) − Vγ
> 0 ⇒ Vin ( t ) − Vγ > 0
R1 + R2
risulta:
V i n ( t ) > V γ ⇒ t > 0 .3 m S
AV ≈ −
(R L / /R C)
4992
.Ω
=−
= −0254
.
RE
1960Ω
Quindi il diodo è in inversa per t<3 mS , ovvero si comporta come un circuito aperto e non lascia
passare corrente.
La tensione VOUT è pertanto nulla.
Per t>3mS la tensione VOUT è:
R2I = R 2
Vin (t ) − Vγ
R1 + R2
= VOUT (t )
Quando VIN=3.6V e per I = 10 -2° abbiamo che
(R1 + R2 ) =
Vin (t ) − Vγ
I
=
3 .6V − 0.6V
= 300 Ω
0.01 A
Da questo diagramma si evidenzia che gli stati della FSM sono nove; di conseguenza le variabili di
stato sono quattro: infatti, indicando con N il numero degli stati e n il numero delle variabili di stato,
una volta noto il valore di N, n sarà il numero più piccolo che rispetterà tale legge: 2n>N. In questo
caso 20 = 1 < 9,
2 1 = 2 < 9, 2 2 = 4 < 9, 2 3 = 8 < 9, 2 4 = 16 >9. Da ciò il numero delle variabili
di stato risulta essere 3.
Svolgimento DGT1
1. Disegnare il diagramma ASM
1. scrivere la tabella della FSM
0
Z=0,U=0,D=0.T=0
IN
IN
0
1
0
1
0
1
0
1
0
1
1
Z=0,U=0,D=0.T=0
SP S 0
a
0
a
0
b
0
b
0
c
0
c
0
d
0
d
0
e
1
e
1
S1
0
0
0
0
1
1
1
1
0
0
S2
0
0
1
1
0
0
1
1
0
0
ZERO UNO
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
DUE TRE S F S*0
0
0
a
0
0
0
b
0
0
0
a
0
0
0
c
0
0
0
d
0
0
0
e
1
0
0
a
0
1
0
a
0
0
0
a
0
0
1
a
0
S*1
0
0
0
1
1
0
0
0
0
0
S*2
0
1
0
0
1
0
0
0
0
0
2. disegnamo la relativa struttura della FSM
0
IN
1
Z=0,U=0,D=0.T=
0
0
Z=0,U=0,D=0.T=0
1
IN
Z=0,U=0,D=0.T=0
3. Posto che il Flip/Flop in figura sia di tipo J K, abbiamo la seguente tabella di eccitazione:
0
Z=
1
0
IN
U=
1
IN
Q(j)
Q ( j+1)
J
K
0
0
1
1
0
1
0
1
0
1
-
1
0
1
1
D=
1
T=
1
La tabella per lo stato S0 , ad esempio, diventa:
IN
0
1
0
1
0
1
0
1
0
1
SP S 0
a
0
a
0
b
0
b
0
c
0
c
0
d
0
d
0
e
1
e
1
S1
0
0
0
0
1
1
1
1
0
0
S2
0
0
1
1
0
0
1
1
0
0
ZERO UNO DUE
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
1
0
0
0
0
TRE SF
0
a
0
b
0
a
0
c
0
d
0
e
0
a
0
a
0
a
1
a
S*0
0
0
0
0
0
1
0
0
0
0
S*1
0
0
0
1
1
0
0
0
0
0
S*2
0
1
0
0
1
0
0
0
0
0
J S0
0
0
0
0
0
1
0
0
-
K S0
1
1
Svolgimento DGT2
Come prima cosa viene indicato con C l’uscita della prima porta logica NOR, e la tabella di verità
del NOR :
C
A
0
0
1
1
B
0
1
0
1
NOR
1
0
0
0
Facendo la mappa di Karnaugh otteniamo:
- per J, utilizzando la sintesi NOR-NOR e raccogliendo le indifferenze cerchiate come zero e le
restanti come 1
IN S 0
S 1S 2
00
01
11
10
00
0
0
01
0
0
11
0
0
Successivamente si riportano gli andamenti temporali di A e di B; di seguito si calcolerà
l’andamento temporale di C e di X.
10
0
1
A
J = S 2 ⋅ S1 ⋅ IN = S 2 ⋅ S1 ⋅ IN = S 2 ⋅ S1 ⋅ IN
-per K, sempre attraverso una NOR-NOR e raccogliendo le indifferenze cerchiate come zero e le
restanti come 1
S 1S 2
IN S0
00
01
11
10
00
1
1
-
01
-
11
-
K = S0
S1S2
00
01
11
10
00
0
0
0
0
01
0
0
ZERO
11
1
0
C
X
10
-
Se sintetizziamo una uscita dobbiamo anche in questo caso considerare l’ingresso, poiché si tratta
di una macchina di Mealy. Ad esempio sintetizziamo ZERO:
IN S 0
B
10
0
0
= S 1 ⋅ IN ⋅ S 2 = S 1 ⋅ IN ⋅ S 2 = S 1 + IN + S 2
Prova Scritta del 23/05/01
DGT1 Punti[10/30]
AN1 Punti[9/30]
Si Progetti una FSM sincrona con la seguenti caratteristiche:
due ingressi sincroni: INPUT 1 e INPUT 2
una uscita
: OUT
L’uscita OUT è normalmente a 0; in ogni periodo di CK la FSM verifica se i due ingressi sono uguali. Se gli
ingressi sono uguali per tre periodo consecutivi di CK successivi durante i quali non verifica l’eguaglianza
degli ingressi.
Si chiede di:
a) disegnare il diagramma ASM
b) scrivere la tabella della FSM
c) sintetizzare almeno variabili di stato e l’uscita OUT
Sia dato il seguente circuito:
V CC
V CC=5 V
I1
IC
CB
V IN
I2
I 0c = 10 mA
RC
V 0CE=2.5 V
CC
IB
R2 VE
IE
RE
V 0E=1 V
β F =100
RL
R L =300 Ω
DGT2 Punti[5/30]
Sia dato il seguente circuito:
Si chiede
a) calcolare i valori della resistenza affinché il transistore sia polarizzato in ZAD
IN
b) calcolare il guadagno in centro banda ai piccoli segnali.
OUT
AN2 Punti[6/30]
Sia dato il circuito in figura e la forma d’onda V1(t) e V2(t) indicata:
IN
V2(t)
1
Ogni porta logica ha un ritardo di propagazione di 10 µs. Si disegni il segnale di uscita OUT
conseguente al segnale di ingresso IN rappresentato in figura.
10
R
VO
V 1 (t)
V1 (t)[V]
5
R = 180 Ω
Diodo : Vγ = 0.6 V
R f = 20 Ω
Tracciare V0 (t) per 0 ≤ t ≤ 4 ms
Nota: Si supponga istantanea la commutazione del diodo.
1
2
3
4
5
T[ms]
30
T[ µs]
Svolgimento AN 1
RC =
Vcc=5V
V CE =2.5V
Ic = 10mA
V E =1V
β f =100
RL =300Ω
VBC + I1 R1 (340Ω ⋅10−2 A)V-1.9V
=
= 150Ω
IC
0.01 A
2) per calcolare il guadagno in centro banda dobbiamo prima disegnare il circuito equivalente ai
piccoli segnali
1)Calcolare le resistenze in ZAD.
Se siamo in ZAD possiamo supporre VBE = 0.6 V e da questa ricaviamo attraverso la KVL
applicata al transistor la tensione VBC :
V BC = V BE - V CE = 0.6V-2.5V= 1.9V
Poi calcoliamo le correnti IB ed I E .
IB =
Ic
βf
=
10 m A
100
= 0 .1m A
IE = IB (βf +1)= 10.1 mA
Calcolo le resistenze:
e calcolare i parametri ai piccoli segnali, ovvero hie e h fe .
Supponiamo VT =25mV
h ie=
VE = IE RE
e quindi la resistenza
RE =
VE
=99Ω
IE
Per determinare R1 ed R2 immaginiamo IB << I 1 , I2 e che I1 ˜ I 2 (dalla KCL applicata al nodo B).
Sapendo che IB=0.1 mA, poniamo I1 ˜ I 2 =10 mA
In questo modo possiamo calcolare le due resistenze R 1 ed R 2 attraverso la KVL.
mentre hfe = βf =100 ma solo numericamente.
Applichiamo ora la KVL al circuito ai piccoli segnali per trovare V out e V in ed il loro rapporto AV che
rappresenta il guadagno di tensione in centro banda.
La Vout sarà data da:
V out = hfe ib (RC //RL )
mentre :
I2 R2 = VE + VBE
Da cui consegue che
R2=
VE + VBE 16
.V
=
= 160Ω
I2
10mA
V in= i b hie + (ib + hfe i b ) R E
Da cui ricaviamo i b in funzione di Vin:
ib
Ed applicando nuovamente KVL al ramo con VCC e le due resistenze R1 ed R 2 otteniamo:
R1 =
VCC − I 2 R2 5V-1.6V
=
= 340Ω
I1
0.01 A
VT 25mV
=
= 250Ω
IB
0,1mA
=
(
V in
)
h ie + 1 + h fe R E
Sostituendo poi in V out troviamo che :
V out= −
La resistenza RC sarà quindi:
E quindi Av sarà uguale a:
Vin
hie + (1 + hfe ) RE
hfe (R L / /RC)
AV =
Vout
h (R / /RC)
= − fe L
Vin
hie + (1 + hf e ) RE
Svolgimento AN2
Il parallelo tra RC ed RL vale:
V1 (t)[V]
5
RCRL
150 ⋅ 300
=
= 100Ω
RC + RL
450
ma dato che h i e << (1+ hfe ) e che h fe ˜ (1+ hfe )
AV ≈ −
1
risulta:
(R L / /RC )
100Ω
=−
= −101
.
RE
99Ω
2
3
4
5
T[ms]
Per prima cosa bisogna ridisegnare il circuito nel modello ai grandi segnali del diodo:
V
γ
R
f
R
V 1(t)
V 2( t )
Adesso, considerando singolarmente istante per istante, si può calcolare il valore di Vout (t) per poi andare a
graficarne l’andamento temporale.
Per 0 ms < t < 1 V1(t) = 0 V, V2 (t) = 5 V
In questo caso bisogna fare delle ipotesi: Ipotizziamo che il diodo lavori in diretta. Sotto tale ipotesi
possiamo scrivere l’equazione della KVL:
V1 (t ) −V γ − IR f − IR − V2 (t ) = 0
Da cui si ricava il valore della corrente:
I=
V1 − Vγ − V2 0 − 0. 6V − 5V
=
= −28mA
R + Rf
180 + 20
Tale valore di corrente (negativo) evidenzia che l’ipotesi considerata è scorretta e che il diodo lavora in
inversa. In tali condizioni si può rappresentare il diodo come un circuito aperto. Di conseguenza, non
essendoci corrente che circola nel circuito, il valore di Vout coinciderà con il valore di V2(t) (5 V). Se si fosse
preso in considerazione l’ipotesi che il diodo lavorava in inversa si avrebbe raggiunto la medesima
conclusione. Infatti la condizione che doveva essere verificata in tale ipotesi era che la differenza di
potenziale ai capi del diodo doveva essere < 0.6 V. (cosa abbastanza facile a dimostrare in quanto essendo il
circuito aperto, sotto tale ipotesi, la differenza di potenziale ai capi del diodo sarebbe stata pari a V1 (t) -V2(t),
cioè = 0).
Per 1 ms < t < 2ms
V 1(t) = 5 V, V 2(t) = 0 V
il diodo lavora in diretta, quindi per calcolare il valore di V out considero il circuito ai grandi segnali e imposto
la KVL:
V1 (t ) − V γ − IR f − IR = 0
Da cui si ricava il valore della corrente:
I=
V1 ( t) − Vγ
Rf + R
=
5 − 0 .6
= 0. 022 A
20 + 180
Infine si ricava Vout semplicemente attraverso la maglia:
Vout ( t) − IR = 0
Vout ( t) = 0. 022* 180 = 3. 96V
Per 2 ms < t < 3 ms
V 1(t) = 5 V, V2(t) = 5 V
Dopo aver esaminato il caso precedente risulta evidente che anche in questo caso il diodo lavori in inversa e
quindi che il valore di V out sia pari a 5 V.
Imfatti applicando la KVL troviamo nuovamente un valore negativo per la corrente
I=
Per t > 3 ms
V1 ( t) − Vγ −V 2 (t )
Rf + R
=
5 − 0 .6 − 5
= −0 .003A
20 + 180
V1(t) = 0 V, V2(t) = 0 V
Non essendoci tensione è ovvio che il valore di V out sia nullo.
GRAFICO FINALE
IN1
0
0
1
1
0
0
1
1
0
0
1
1
-
Svolgimento DGT 1
In primo luogo disegnamo il diagramma ASM
IN2
0
1
0
1
0
1
0
1
0
1
0
1
-
S0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
S1
0
0
0
0
0
0
0
0
1
1
1
1
1
0
0
S2
0
0
0
0
1
1
1
1
0
0
0
0
1
0
1
SP
a
a
a
a
b
b
b
b
c
c
c
c
d
e
f
OUT
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
S’0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
S’1
0
0
0
0
1
0
0
1
1
0
0
1
0
0
0
S’2
1
0
0
1
0
0
0
0
1
0
0
1
0
1
0
SF
b
a
a
b
c
a
a
c
d
a
a
d
e
f
a
Vista la tabella FSM disegnamo la macchina di Moore relativa:
IN1
RC1
RC2
4
IN2
3
6
Sintetizziamo l’uscita OUT ed uno stato, ad esempio S0.
L’uscita non dipende dagli ingressi ma soltanto dalle variabili si sato poiché si tratta di una
macchina di Moore:
S 1S 2
00
01
11
10
0
0
0
1
0
1
1
1
-
-
S0
Quindi scriviamo la relativa tabella FSM, tenedo conto del fatto che, avendo 5 stati (a,b,c,d,e)
abbiamo 3 variabili di stato poiché 2 3 > 6 e 2 2 <6 .
OUT
1
Considerando l’indifferenza cerchiata come un 1 e la rimanente come uno 0 otteniamo la seguente
sintesi di OUT:
OUT = S 0 S 1 + S 1 S 2
Svolgimento DGT 2
Abbiamo il seguente circuito e l’ingresso dato .
Lo stato, ad esempio S0 , dipende invece anche dagli ingressi:
OUT
S 0S 1S 2
IN1 IN2
00
01
11
10
000
0
0
0
0
001
0
0
0
0
011
1
1
1
1
010
0
0
0
0
110
-
111
-
101
0
0
0
0
100
1
1
1
1
A
IN
C
B
1
Ogni componente logico ha un ritardo di 10 mS
10
Notiamo però che la variabile S’0 è anch’essa indipendente dagli ingressi .
La sua sintesi sarà:
S ′0 = S0 S 1 S 2 + S 0 S 1 S 2
30
IN
10
30
T[mS]
A
20
40
T[mS]
B
30
50
T[mS]
C
20
60
T[mS]
OUT
20
70
T[mS]
T[ µs]
Prova Scritta del 27/11/01
AN1 Punti[11/30]
Dato il seguente circuito e le caratteristiche (VCE , IC) del grafico allegato, si chiede di calcolare:
VCC = 3 V
I1
RC
R1
I0 C = 1.5 mA
V0 CE = 1 V
IC
VCE
IB
I2
R2
V0 BE = 0.7 V
IE
V CC
RE = 1000 Ω
R1 = 50000 Ω
Rb ≅ 0 Ω
RE
VT = 0.025 V
1. il valore di α f, β f
2. il valore di correnti del circuito nel punto di lavoro
3. il valore dei parametri de l circuito equivalente del transistore ai piccoli segnale nel punto di lavoro
trovato.
AN2 Punti[4/30]
Siano dati il seguente circuito e gli andamenti temporali di V1 (t) e V2 (t) specificati in seguito. Si chiede di
calcolare e disegnare l’andamento temporale di Vo (t) nell’intervallo: 0 ms ≤ t ≤ 4 ms. Si consideri la
commutazione del diodo istantanea ed i seguenti valori del modello ai grandi segnali del diodo: Vγ = 0.6 V,
Rf ≅ 20 Ω, Is = 0 A, Rr ≅ ∞ Ω ed inoltre R = 180 Ω
V1 (t)[V]
5
R
1
V1(t)
VO(t)
V2(t)
2
3
4
5
T[ms]
DGT1 Punti[12/30]
Si consideri un attraversamento pedonale stradale: su entrambe le corsie della strada sono posti dei sensori
che individuano la presenza di veicoli in transito (segnale SENS = 1). L’attraversamento pedonale è regolato
da un impianto semaforico.
Si progetti una FSM sincrona per la gestione dell’impianto semaforico: la FSM ha due segnali di ingresso:
Ø SENS: proveniente dai sensori che individuano la presenza di veicoli in transito (SENS = 1 se sono
presenti veicoli in transito)
Ø PULS: Proveniente dal pulsante di ric hiesta di attraversamento pedonale (PLUS = 1 se è stato premuto
il pulsante)
e cinque segnali di uscita:
Ø AVANTI: segnale che accende la scritta AVANTI (AVANTI = 1) per permettere l’attraversamento dei
pedoni
Ø STOP: segnale che accende la scritta STOP (STOP = 1) che vieta l’attraversamento dei pedoni
Ø V: segnale che accende la luce verde (V = 1) per permettere il passaggio dei veicoli
Ø G: segnale che accende la luce gialla (G = 1) per i veicoli
Ø R: segnale che accende la luce rossa (R = 1) per vietare il passaggio dei veicoli.
Normalmente il semaforo è nella condizione di stop (STOP = 1) per i pedoni mentre viene consentito il
passaggio ai veicoli (V = 1). Se sono presento veicoli in transito (SENS =1) il semaforo permane in tale
condizione. Se non sono presenti veicoli in transito (SENS = 0) e non è attivata la richiesta di
attraversamento da parte dei pedoni (PULS = 0) il semaforo permane nella condizione attuale. Se SENS = 0
e PLUS = 1 il semaforo attiva la procedura per promettere l’attraversamento, ovvero in sequenza:
Ø Condizione di stop (STOP = 1) e luce gialla accesa (G = 1)
Ø Condizione di stop (STOP = 1) e luce rossa accesa (R = 1)
Ø Condizione di attraversamento consentito (AVANTI = 1, R = 1)
Giunto in questa condizione il semaforo verifica se è riattivata la condizione di attraversamento ( PLUS = 1):
in tal caso rimane nella condizione attuale. Altrimenti (PULS = 0) il se non ci sono veicoli in transito (SENS
= 0) il semaforo permane nella situazione attuale; se sono presenti veicoli in transito (SENS =1) allora il
semaforo si porta nella condizione STOP = 1, R = 1, e poi torna nella situazione iniziale STOP = 1, V = 1.
Si progetti una FSM utilizzando la struttura di Moore. Si richiede di :
1. disegnare il diagramma ASM
2. scrivere la tabella della FSM
3. disegnare la struttura della FSM
4. sintetizzare almeno una uscita ed una variabile di stato (utilizzare FF di tipo JK “edge sensitive” e
sintesi di tipo NOR-NOR).
DGT2 Punti[3/30]
Dato il seguente circuito (tre FF di tipo T “edge sensitive”) si chiede di disegnare l’andamento temporale
delle uscite Q1 , Q2 , Q3 in relazione al segnale di CK per almeno nove periodo di CK (si suppongano le tre
uscite inizialmente uguali a zero). Gli ingressi T1 , T2 , T3 sono posti ad 1.
1
1
T1 Q
CK
CK
1
1
T2 Q
2
T3
Q
3
Svolgimento AN 1
Vcc=3 V
VBE =0.7 V
IC = 1.5 mA
VCE =1V
RE =1 kΩ
R1=50 kΩ
Rb ˜ 0
VT=25mV
1)Calcolare αf
αf =
βf
1 + βf
=
150
= 0.99
151
Poi calcoliamo VBC avendo VCE e VBE
VBC = V BE – VCE = 0.7V - 1V= -0.3V
Poi calcoliamo le correnti IB ed IE .
IC
βf
IB =
= 1.155m0A = 10 µ A
I E =I C + I B = 1.51 mA
Calcolo le correnti e le resistenze attraverso le KVL:
I 1R1 = V BE + I E RE
e quindi la corrente
I1 =
I E R E + VBE
= 44µΑ
R1
Avendo I1 ed IB possiamo calcolare I2 attraverso la KCL:
I2 = IB+I1=44+10 µΑ=54µΑ
Da cui consegue che
R2 =
VCC - R1I1 08
.V
=
= 14815Ω
I2
54µA
Avendo IC , I2 , R2 e VBC calcoliamo RC :
RC =
I 2 R2 + VBC 0.8V − 0.3V
=
= 333Ω
IC
15
. mA
2) disegnamo il circuito equivalente ai piccoli segnali:
e calcoliamo i parametri ai piccoli segnali, ovvero hi e e hf e .
rπ =
VT
25mV
=
= 2500Ω
I B 0,01mA
hie = rπ + Rb =2500Ω
mentre hfe
= βf =150 ma solo numericamente.
Svolgimento AN2
Per prima cosa bisogna ridisegnare il circuito nel modello ai grandi segnali del diodo:
V
R
γ
f
R
V 1(t)
V 2(t)
Adesso, considerando singolarmente istante per istante, si può calcolare il valore di Vout (t) per poi
andare a graficarne l’andamento temporale.
Per 0 ms < t < 1 ms
V1(t) = 5 V, V2(t) = 0 V
il diodo lavora in diretta, quindi per calcolare il valore di Vout considero il circuito ai grandi segnali e
imposto la KVL:
V1 (t ) − Vγ − IR f − IR = 0
Da cui si ricava il valore della corrente:
I=
V1 ( t ) − Vγ
Rf + R
=
5 − 0 .6
= 0.022 A
20 + 180
Infine si ricava Vout semplicemente attraverso la maglia:
Vout (t ) − IR = 0
Vout (t ) = 0.022 *180 = 3.96V
Per 1 ms < t < 2ms
V1(t) = 5 V, V2(t) = 5 V
In questo caso bisogna fare delle ipotesi: Ipotizziamo che il diodo lavori in diretta. Sotto tale ipotesi
possiamo scrivere l’equazione della KVL:
V1 (t ) − Vγ − IR f − IR − V2 ( t ) = 0
Da cui si ricava il valore della corrente:
I=
V1 (t ) − Vγ − V2 (t )
Rf + R
=
5 − 0 .6 − 5
= −0.003 A
20 + 180
Tale valore di corrente (negativo) evidenzia che l’ipotesi considerata è scorretta e che il diodo
lavora in inversa. In tali condizioni si può rappresentare il diodo come un circuito aperto. Di
conseguenza, non essendoci corrente che circola nel circuito, il valore di Vout coinciderà con il
valore di V2(t) (5 V). Se si fosse preso in considerazione l’ipotesi che il diodo lavorava in inversa si
avrebbe raggiunto la medesima conclusione. Infatti la condizione che doveva essere verificata in
tale ipotesi era che la differenza di potenziale ai capi del diodo doveva essere < 0.6 V. (cosa
abbastanza facile a dimostrare in quanto essendo il circuito aperto, sotto tale ipotesi, la differenza
di potenziale ai capi del diodo sarebbe stata pari a V1(t) -V2(t), cioè = 0).
Per 2 ms < t < 3 ms
V1(t) = 0 V, V2(t) = 5 V
Dopo aver esaminato il caso precedente risulta evidente che anche in questo caso il diodo lavori in
inversa e quindi che il valore di Vout sia pari a 5 V.
Per t > 3 ms
V1(t) = 0 V, V2(t) = 0 V
Non essendoci tensione è ovvio che il valore di Vout sia nullo.
GRAFICO FINALE
Vout[V]
5
4
1
2
3
4
5
T[ms]
Svolgimento DGT1
1. disegnare il diagramma ASM della FSM
AVANTI = 0; STOP = 1;
(a)
V = 1; G = 0; R = 0;
1
SENS
0
0
PULS
1
AVANTI = 0; STOP = 1;
(b)
V = 0; G = 1; R = 0;
AVANTI = 0; STOP = 1;
(c)
V = 0; G = 0; R = 1;
AVANTI = 1; STOP = 0;
V = 0; G = 0; R = 1;
1
(d)
PLUS
0
0
SENS
1
AVANTI = 0; STOP = 1;
V = 0; G = 0; R = 1;
(e)
Da questo diagramma si evidenzia che gli stati della FSM sono cinque; di conseguenza le variabili
di stato sono tre: infatti, indicando con N il numero degli stati e n il numero delle variabili di stato,
una volta noto il valore di N, n sarà il numero più piccolo che rispetterà tale legge: 2n>N. In questo
caso 20 = 1 < 5,
21 = 2 < 5, 22 = 4 < 5, 23 = 8 > 5. Da ciò il numero delle variabili di stato
risulta essere 3.
2. scrivere la tabella della FSM
SEN
S
0
0
1
0
1
-
PUL
S
0
1
0
1
0
-
SP S2
a
a
a
b
c
d
d
d
e
0
0
0
0
0
0
0
0
1
S1
S0
0
0
0
0
1
1
1
1
0
0
0
0
1
0
1
1
1
0
AVANTI STOP V
0
0
0
0
0
1
1
1
0
1
1
1
1
1
0
0
0
1
1
1
1
0
0
0
0
0
0
G
R
SF
S*2
S*1
S*2
0
0
0
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
a
b
a
c
d
d
d
e
a
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
0
0
0
1
0
0
1
1
1
0
0
3. Struttura della FSM
IN1
RC1
RC2
4
IN2
3
6
OUT
5
4. Il flip/flop in figura è di tipo J K e quindi per sintetizzare uno stato futuro, ad esempio
S’0 , dobbiamo utilizzare la tabella di eccitazione e scrivere il valore di J e di K
relativi al passaggio dallo stato (n) allo stato (n+1).
Q(j)
Q ( j+1)
J
K
0
0
1
1
0
1
0
1
0
1
-
1
0
SENS PUL
S
0
0
0
1
1
0
0
1
1
0
-
SP S2 S1
a
a
a
b
c
d
d
d
e
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
0
S0 AVANTI
0
0
0
1
0
1
1
1
0
STOP V
0
0
0
0
0
1
1
1
0
1
1
1
1
1
0
0
0
1
1
1
1
0
0
0
0
0
0
G
R
SF
S*2
S*1
S*2
JS0
KS0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
a
b
a
c
d
d
d
e
a
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
0
0
0
1
0
0
1
1
1
0
0
0
0
0
0
0
0
0
1
-
1
E quindi avrò le seguenti mappe di Karnaugh per le due variabili:
- per J
S0S1S2
000
0
0
0
0
Sens Puls
00
01
11
10
001
0
0
0
0
011
0
0
0
1
010
0
0
0
0
110
-
111
-
101
-
100
-
Considero le indifferenze cerchiate come zeri mentre le restanti come 1 e applico la sintesi
NOR-NOR:
(
)
(
)
J = ( S 0 + S1 ) ⋅ (SENS ) ⋅ (S 0 + S1 + S 2 ) ⋅ PULS = ( S 0 + S1 ) ⋅ ( SENS ) ⋅ (S 0 + S1 + S 2 ) ⋅ PULS =
= ( S 0 + S1 ) + (SENS ) + (S 0 + S1 + S 2 ) + PULS
-per K
S0S1S2
Sens Puls
00
01
11
10
000
-
001
-
011
-
010
-
110
-
111
-
101
-
100
1
1
1
1
Considero nuovamente le indifferenze cerchiate come zeri mentre le restanti come 1.
K=S0
Per quanto riguarda la sintesi di una uscita, non ho bisogno di guardare gli ingressi in quanto si
tratta di una Macchina di Moore.
Prendiamo ad esmpio l’uscita Giallo:
S1 S2
00
01
11
10
0
0
1
0
0
1
0
-
-
-
S0
G = S 2 ⋅ S1 = S 2 ⋅ S1 = S 2 + S1
Svolgimento DGT2
Il Flip-Flop Toggle “edge sensitive” ad ogni colpo di clock nega lo stato in memoria. Nel risolvere
l’esercizio bisogna tener presente che ogni uscita del FF precedente diventa CK per il FF
successivo.
CK
IN
Q1
Q2
Q3
DGT1 Punti[9/30]
Prova scritta del 5/09/2001
AN1 Punti[7/30]
Si progetti un contatore “modulo 3” che possiede due ingressi IN1, IN2, ed un’uscita LED. In ogni stato il
contatore verifica se la configurazione degli ingressi coincide con il codice dello stato; in caso affermativo il
contatore manda l’uscita LED ad 1 ed attende fino a che gli ingressi non cambiano; nel qual caso il contatore
prosegue il conteggio. Nel caso in cui la configurazion e degli ingressi non coincide con il codice dello stato
il contatore prosegue il conteggio.
Sia dato il seguente circuito:
D 1, D2 “ideali”
Vγ = 0 V
Rf = 0 Ω
Rr = ∞ Ω
DGT2 Punti[6/30]
Is = 0 A
Sia data la seguente rete logica:
V R1 = 6 V
V R2 = 12 V
U
V s = 3*103 t V, per t >0
8ms
T
A
C
8ms
8ms
V
Si chiede di disegnare l’andamento temporale di Vout(t) per t >0.
8ms
Punti[7/30]
B
8ms
8ms
8ms
40ms
AN2 Punti[8/30]
Dato il seguente circuito:
Per ogni porta lodica sono dati i seguenti tempi di propagazione. Si disegni l’andamento temporale dei
segnali A, B, C, OUT in corrispondenza della transazione degli ingressi:
V CC= 5 V
I0C= 10 mA
T:
U:
C:
V 0E = 1 V
V 0CE = 2.5 V
RL = 1 kΩ
β = 100
Si chiede:
a) Calcolare i valori della resistenza nel punto di lavoro (ZAD)
b) Calcolare il guadagno in centro banda ai piccoli segnali
Punti [8/30]
1
1
1
0
1
1
Svolgimento AN 1
Il grafico di Vs è il seguente:
[V]
12
29
6
3
1
2
3
4
5
t[ms]
Ciò significa che, dato che la tensione VS, per t< 2ms, è Vs<6V ovvero VS<VR1 il diodo1 è in
inversa fino a quando t<2ms.
Il diodo2, orientato in modo opposto al diodo1 è in diretta fino a quando VS <4ms ovvero V S<12V
che è il valore del generatore V R1 .
1) Per t compreso tra 0 e 2 ms abbiamo quindi il seguente circuito:
dato che Vγ=0 e R f =0, il diodo in diretta è assimilabile ad un corto-circuito, mentre dato Rr=+8 il
diodo in inversa è un circuito aperto.
La VOUT misurata è quindi uguale a VR2 ovvero VOUT =12V
2) Per t compreso tra 2 e 4 ms abbiamo anche il diodo1 in diretta poiché la tensione ai suoi capi
diventa positiva. VOUT è ancora uguale a VR2 come si arguisce senza difficoltà alcuna dal
disegnoe quindi VOUT =12V:
3) per t>4ms il diodo2 va in inversa, essendo Vs> VR2 , ed il cicuito diventa
In questo caso V OUT = V R1 ovvero VOUT =6V
Ricapitolando:
Per t<4ms abbiamo che VOUT =12V mentre per t>4ms VOUT =6V
Svolgimento AN2
R1 =
Vcc=5V
V CE =2.5V
Ic = 10mA
V E =1V
β f =100
RL =1kΩ
ICR c − VBC 1.5V - (-1.9V)
=
= 340Ω
I1
0.01A
2) per calcolare il guadagno in centro banda dobbiamo prima disegnare il circuito equivalente ai
piccoli segnali
1)Calcolare le resistenze in ZAD.
Se siamo in ZAD possiamo supporre VBE = 0.6 V e da questa ricaviamo attraverso la KVL
applicata al transistor la tensione VBC :
V BC = V BE - V CE = 0.6V-2.5V= 1.9V
Poi calcoliamo le correnti IB ed I E .
Ic
βf
IB =
=
10 m A
100
= 0 .1m A
IE = IB (βf +1)= 10.1 mA
e calcolare i parametri ai piccoli segnali, ovvero hie e h fe .
Calcolo le resistenze:
VE = IE RE
e quindi la resistenza R
E
VE
=
IE
h ie=
=99Ω
Calcoliamo quindi R C attravrso la KVL:
VCC-I CRC- V CE -V E
VT 25mV
=
= 250Ω
IB
0,1mA
mentre hfe = βf =100 ma solo numericamente.
Applichiamo ora la KVL al circuito ai piccoli segnali per trovare V out e V in ed il loro rapporto AV che
rappresenta il guadagno di tensione in centro banda.
La Vout sarà data da:
V out = h fe ib RC
Da cui segue che
Rc =
VCC - VE − VCE 5V -1V- 2.5V
=
= 150Ω
IC
0.01A
mentre :
V in= i b hie + (ib + hfe i b ) R E
Da cui ricaviamo ib in funzione di Vin:
Per determinare R1 ed R 2 immaginiamo IB << I1 , I 2 e che I1 ˜ I2 (dalla KCL applicata al nodo B). Sapendo
che IB=0.1 mA, poniamo I 1˜ I2 =10 mA
In questo modo possiamo calcolare le due resistenze R1 ed R2 attraverso la KVL.
ib
=
(
V in
)
h ie + 1 + h fe R E
I2 R2 = VE + VBE
Sostituendo poi in V out troviamo che :
Da cui consegue che
R2=
Ed
VE + VBE 16
.V
=
= 160Ω
I2
10mA
V out= −
E quindi Av sarà uguale a:
Vin
hie + (1 + hfe ) RE
hfe (R L / /RC)
a
LED=0
Svolgimento DGT 1
V
h (R / /RC)
AV = out = − fe L
Vin
hie + (1 + hf e ) RE
0
0
IN1
Il parallelo tra RC ed RL vale:
IN2
1
R CR L
150 ⋅1000
=
= 130 .5Ω
R +R
1150
C
L
ma dato che h i e << (1+ hfe ) e che h fe ˜ (1+ hfe )
1
LED=0
risulta:
b
LED=
11
(R //R )
130.5Ω
AV ≈ − L C = −
= −1.32
RE
99Ω
0
IN1
IN2
1
0
LED =
0
c
LED=
10
1
IN1
IN2
1
0
LED=0
Abbiamo utilizzato una macchina di Mealy che conta tre stat i(a,b,c) e manda Led=1 se lo stato
coincide con gli ingressi.
Dato che abbiamo tre stati, il numero di variabli di stato è due (S 0 ed S1 ). Infatti 22 = 4>3 mentre21
=2<3.
La tabela relativa é:
IN1
0
0
1
0
0
1
0
1
1
IN2
0
1
0
1
0
1
SP
A
A
A
B
B
B
C
C
C
S0
0
0
0
0
0
0
1
1
1
S1
0
0
0
1
1
1
0
0
0
S0 ’
0
0
0
1
0
1
0
1
0
LED
1
0
0
0
1
0
0
1
0
S 1’
0
1
1
0
1
0
0
0
0
E la sua sintesi NAND-NAND è, considerando le indifferenze raggruppate come 1 e le rimanenti
come 0:
SF
a
b
b
c
b
c
a
c
a
OUT = S0 S 1 IN 1 IN 2 + S 1 IN 1 IN 2 + S 0 IN 1 IN 2
Svolgimento DGT 2
T
0 mS
E questo è il diagramma FSM della macchina di Mealy richiesta, ponendo un Latch delay
all’ingresso e un Latch Per la Gestione Master-Slave degli stati:
U
4
IN1
4
IN2
RC1
2
4
RC2
OUT
V
_
U
Sintetizziamo infine uno stato e la variabile di uscita OUT rispetto ai due ingressi e allo stato.
Questo va fatto anche per l’uscita OUT poiché, trattandosi di una macchina di Mealy, l’uscita
dipende anche dagli ingressi e non solo dallo stato attuale.
Facciamo la mappa di Karnaugh di S’0
00
01
11
10
00
0
0
0
0
01
1
0
1
1
11
-
_
T
8 mS
10
0
0
0
1
A
8 mS
La sua sintesi sarà, considerando le indifferenze raggruppate come 1 e le restanti come zeri.:
B
S ' 0 = IN1 S 1 + S 2 IN 2 + S 0 IN 1 IN 2
16 mS
L’uscita OUT sarà invece :
00
00
1
01
0
11
-
10
0
01
0
1
-
0
11
10
0
0
0
0
-
0
1
C
24 mS
_
T
40mS