Prova scritta di Misure Elettriche NO 12 dicembre 2012

Prova scritta di Misure Elettriche NO del 12_dicembre_2012
1. Una forma d’onda sinusoidale è descritta dall’equazione: vt   5.2 sin 7540 t ) V  . Dopo averla disegnata trovare
tensione di picco, efficace, valor medio raddrizzato, frequenza e periodo. Se applichiamo tale tensione ai capi di una
resistenza da 10   1%, qual è la potenza dissipata sulla resistenza? esprimere tale valore anche in dBm. Parlare
inoltre del massimo trasferimento di tensione e di potenza tra strumento e circuito di misura chiarendo con i grafici.
2. Con un multimetro numerico con accuratezza (510-2Vletta+210-2Vfs) si rilevano le seguenti letture di tensione in V
ai capi di R = 840 b  1 %:
4.9; 5.1; 4.6; 5.0; 5.1; 4.7; 4.4; 4.7; 4.6
Trovare la misura della corrente che scorre all’interno di R. Parlare inoltre del ponte di Wheatstone e delle incertezze
coinvolte.
3. Si ha a disposizione un convertitore analogico/digitale ad approssimazioni successive con le seguenti caratteristiche:
fondo scala: 10V; risoluzione 14 bit
Determinare schema a blocchi, funzionamento e cause di incertezza nel caso in cui si misura una tensione continua di
3V nominali
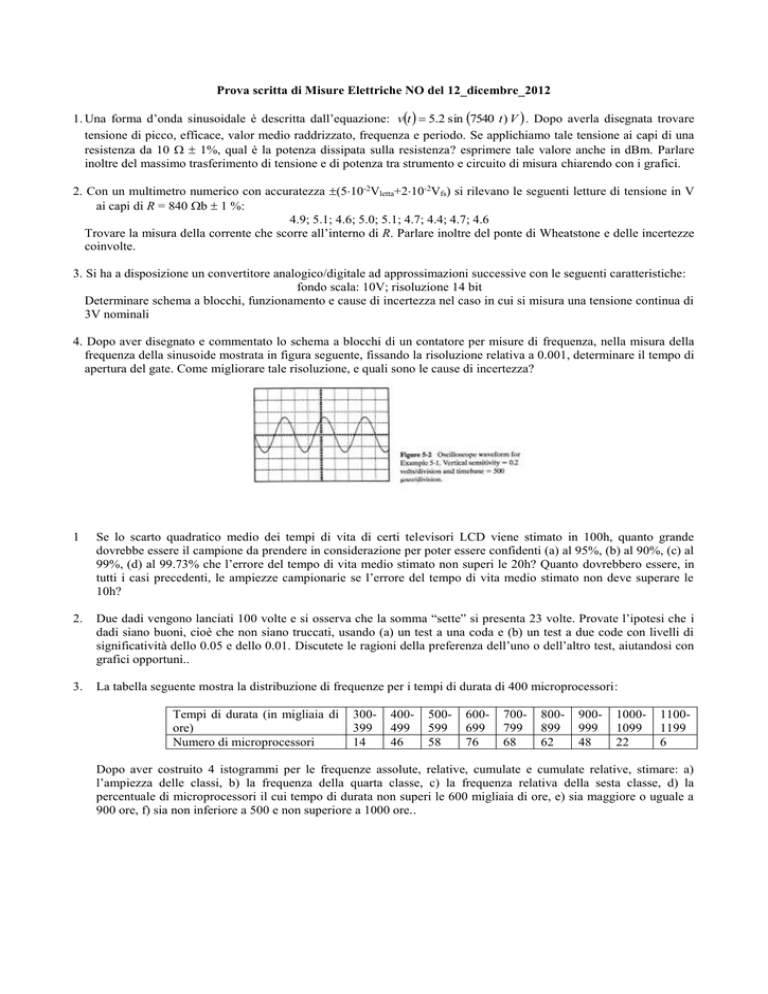
4. Dopo aver disegnato e commentato lo schema a blocchi di un contatore per misure di frequenza, nella misura della
frequenza della sinusoide mostrata in figura seguente, fissando la risoluzione relativa a 0.001, determinare il tempo di
apertura del gate. Come migliorare tale risoluzione, e quali sono le cause di incertezza?
1
Se lo scarto quadratico medio dei tempi di vita di certi televisori LCD viene stimato in 100h, quanto grande
dovrebbe essere il campione da prendere in considerazione per poter essere confidenti (a) al 95%, (b) al 90%, (c) al
99%, (d) al 99.73% che l’errore del tempo di vita medio stimato non superi le 20h? Quanto dovrebbero essere, in
tutti i casi precedenti, le ampiezze campionarie se l’errore del tempo di vita medio stimato non deve superare le
10h?
2.
Due dadi vengono lanciati 100 volte e si osserva che la somma “sette” si presenta 23 volte. Provate l’ipotesi che i
dadi siano buoni, cioè che non siano truccati, usando (a) un test a una coda e (b) un test a due code con livelli di
significatività dello 0.05 e dello 0.01. Discutete le ragioni della preferenza dell’uno o dell’altro test, aiutandosi con
grafici opportuni..
3.
La tabella seguente mostra la distribuzione di frequenze per i tempi di durata di 400 microprocessori:
Tempi di durata (in migliaia di
ore)
Numero di microprocessori
300399
14
400499
46
500599
58
600699
76
700799
68
800899
62
900999
48
10001099
22
11001199
6
Dopo aver costruito 4 istogrammi per le frequenze assolute, relative, cumulate e cumulate relative, stimare: a)
l’ampiezza delle classi, b) la frequenza della quarta classe, c) la frequenza relativa della sesta classe, d) la
percentuale di microprocessori il cui tempo di durata non superi le 600 migliaia di ore, e) sia maggiore o uguale a
900 ore, f) sia non inferiore a 500 e non superiore a 1000 ore..