Raccolta di problemi di geometria piana sul triangolo

Triangoli - 1
Raccolta di problemi di geometria piana sul triangolo
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
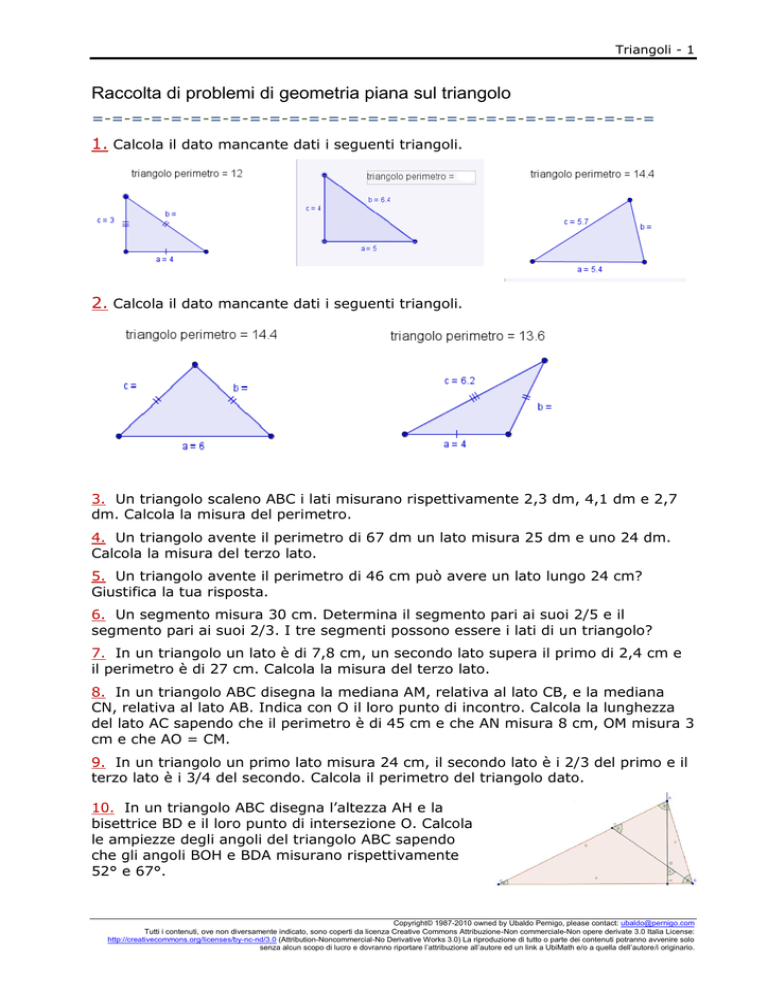
1. Calcola il dato mancante dati i seguenti triangoli.
2. Calcola il dato mancante dati i seguenti triangoli.
3. Un triangolo scaleno ABC i lati misurano rispettivamente 2,3 dm, 4,1 dm e 2,7
dm. Calcola la misura del perimetro.
4. Un triangolo avente il perimetro di 67 dm un lato misura 25 dm e uno 24 dm.
Calcola la misura del terzo lato.
5. Un triangolo avente il perimetro di 46 cm può avere un lato lungo 24 cm?
Giustifica la tua risposta.
6. Un segmento misura 30 cm. Determina il segmento pari ai suoi 2/5 e il
segmento pari ai suoi 2/3. I tre segmenti possono essere i lati di un triangolo?
7. In un triangolo un lato è di 7,8 cm, un secondo lato supera il primo di 2,4 cm e
il perimetro è di 27 cm. Calcola la misura del terzo lato.
8. In un triangolo ABC disegna la mediana AM, relativa al lato CB, e la mediana
CN, relativa al lato AB. Indica con O il loro punto di incontro. Calcola la lunghezza
del lato AC sapendo che il perimetro è di 45 cm e che AN misura 8 cm, OM misura 3
cm e che AO = CM.
9. In un triangolo un primo lato misura 24 cm, il secondo lato è i 2/3 del primo e il
terzo lato è i 3/4 del secondo. Calcola il perimetro del triangolo dato.
10. In un triangolo ABC disegna l’altezza AH e la
bisettrice BD e il loro punto di intersezione O. Calcola
le ampiezze degli angoli del triangolo ABC sapendo
che gli angoli BOH e BDA misurano rispettivamente
52° e 67°.
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 2
11. In un triangolo ABC il lato AB misura 3,2 cm, il lato BC supera AB di 2,2 cm e il
lato BC è inferiore di 0,9 a quest’ultimo. Calcola il perimetro del triangolo. Usando
riga e compasso disegna il triangolo e stabilisci se sia rettangolo, acutangolo o
ottusangolo.
12. In un triangolo un lato misura 1,5 cm e gli altri due sono rispettivamente i 4/3
e i 5/3 del primo lato. Calcola il perimetro del triangolo dato.
13. Calcola l'ampiezza dell'angolo in A di un triangolo ABC sapendo che l'angolo in
B misura 44° e che il terzo angolo è il triplo dell'angolo in B?
14. Calcola le ampiezze degli angoli acuti di un triangolo rettangolo sapendo che le
loro misure differiscono di 34°.
15. In un triangolo ABC l’angolo in A è doppio dell'angolo in B. Sapendo che la
somma dei due angoli è di 114° (A^+B^=114°), determina l'ampiezza di ciascuno
degli angoli interni del triangolo.
16. Calcola le ampiezze degli angoli di un triangolo ABC sapendo che gli angoli in B
e in C superano l'angolo in A rispettivamente di 12° e di 33°.
17. In un triangolo ABC il perimetro misura 48 cm ed è i 32/9 del lato AB, la
lunghezza del lato BC supera quella del lato AC di 1,7 cm. Determina la misura dei
tre lati del triangolo dato.
18. In un triangolo rettangolo ABC, rettangolo in A, il perimetro misura 14,2 cm, il
lato AC misura 3 cm e l’angolo in C è il doppio dell'angolo in B. Determina
l'ampiezza degli angoli interni e la misura dell'ipotenusa del triangolo dato.
19. In un triangolo ABC l'angolo in A supera l'angolo in B di 20° e l'angolo in C è il
doppio dell'angolo in A. Determina l'ampiezza degli angoli interni del triangolo dato.
20. In un triangolo ABC l'angolo in A misura 64° e l’angolo
B è di 34°. Siano date l’altezza CD relativa al lato AB e il
segmento CE, bisettrice relativa allo stesso lato. Determina
l'ampiezza dell’angolo DCE formato dall’altezza e dalla
bisettrice.
21. In un triangolo ABC l'angolo in A misura 106° e
l’angolo in B è di 48°. Calcola l’ampiezza degli angoli che
l’altezza BH forma con i lati BA e BC.
22. In un triangolo ABC l'angolo in A misura 60° e l’angolo in B è i ¾ dell’angolo in
A. Calcola l’ampiezza del terzo angolo del triangolo. Di che triangolo si tratta?
23. Un triangolo equilatero è formato da quattro triangoli equilateri
opportunamente organizzati su due file. Sapendo che il perimetro di uno dei
triangoli equilateri è di 15 cm, calcola la misura di ciascun lato e del perimetro del
triangolo dato.
24. Un triangolo equilatero è formato da nove triangoli equilateri opportunamente
organizzati su tre file. Sapendo che il perimetro di uno dei triangoli equilateri è di
15 cm, calcola la misura di ciascun lato e del perimetro del triangolo dato.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 3
Soluzioni
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Un triangolo scaleno ABC i lati misurano
rispettivamente 2,3 dm, 4,1 dm e 2,7 dm. Calcola la
misura del perimetro.
2p = AB+BC+AC =2,3+4,1+2,7 = 6,4+2,7 = 9,1 dm
AB = 2,3 dm
BC = 4,1 dm
AC = 2,7 dm
2p = ?
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Un triangolo avente il perimetro di 67 dm un lato
misura 25 dm e uno 24 dm. Calcola la misura del
terzo lato.
AC
= 2p – (AB+BC)
= 67 – (25+24) = 67 – 49 = 18 dm
2p = 67 dm
AB = 25 dm
BC = 24 dm
AC = ?
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 4
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Un triangolo avente il perimetro di 46 cm può avere
un lato lungo 24 cm? Giustifica la tua risposta.
2p = 46 cm
AB = 24 cm
È un triangolo?
In un qualsiasi triangolo la misura di un lato non può
essere maggiore o uguale alla somma degli altri due…
BC+AC = 2p – AB = 46-24 = 22 cm
AB > BC+AC
essendo
24 > 22
No, non è un triangolo.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Un segmento misura 30 cm. Determina il segmento
pari ai suoi 2/5 e il segmento pari ai suoi 2/3. I tre
segmenti possono essere i lati di un triangolo?
x = 30 cm
y = 2/5 x
z = 2/3 x
y = 30 /5 * 2 = 6 * 2 = 12 cm
z = 30 / 3 * 2 = 10 * 3 = 30 cm
I tre valori sono lati di un triangolo perché ogni valore dato
è minore della somma degli altri due.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo un lato è di 7,8 cm, un secondo lato
supera il primo di 2,4 cm e il perimetro è di 27 cm.
Calcola la misura del terzo lato.
BC = AB + 2,4 cm = 7,8+2,4 = 10,2 cm
AC
AB = 7,8 cm
BC = AB + 2,4 cm
2p = 27 cm
AC = ?
= 2p – (AB+BC) = 27 - (10,2+7,8) =
= 27 – 18 = 9 cm
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC disegna la mediana AM, relativa
al lato CB, e la mediana CN, relativa al lato AB.
Indica con O il loro punto di incontro. Calcola la
lunghezza del lato AC sapendo che il perimetro è di
45 cm e che AN misura 8 cm, MO misura 3 cm e che
AO è uguale a CM.
AB = AN + BN = 8+8 = 16 cm
Essendo MO = 3 cm si ha
AO = 2*MO = 3*2 = 6 cm
AO = CM = 6 cm
CM = MB = 6 cm
MC = CM + MB = 6+6 = 12 cm
AC = 2p–(AB+BC) = 45 – (6+12) = 45 – 18 = 17 cm
2p = 45 cm
AN = 8 cm
MO = 3 cm
AO = CM
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 5
In un triangolo un primo lato misura 24 cm, il
secondo lato è i 2/3 del primo e il terzo lato è i 3/4
del secondo. Calcola il perimetro del triangolo dato.
BC = 2/3 AB = 24/3*2 = 8*2 = 16 cm
AC = ¾ BC = 16/4*3 = 4*3 = 12 cm
AB = 24 cm
BC = 2/3 AB
AC = ¾ BC
2p = ?
2p = AB+BC+AC = 24+16+12 = 52 cm
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC disegna l’altezza AH e la bisettrice BD e il loro punto di
intersezione O. Calcola le ampiezze degli angoli del triangolo ABC sapendo che gli
angoli BOH e BDA misurano rispettivamente 52° e 67°.
Essendo AH l’altezza il triangolo HOB è rettangolo in
H (90°) per cui l’angolo
Angolo HBO = 180° - 90° - 52° = 38°
Essendo BD la bisettrice, l’angolo BDA = HBO e…
Angolo CBA = 2 * HBO = 2 * 38° = 76°
Angolo BAC = 180° - 67° - 38° = 180° - 105° = 75°
Quindi
Angolo ACB = 180° - 75° - 76° = 180° - 151 = 29°
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC il lato AB misura 3,2 cm, il lato
BC supera AB di 2,2 cm e il lato AC è inferiore di 0,9
cm a quest’ultimo. Calcola il perimetro del triangolo.
Usando riga e compasso disegna il triangolo e
stabilisci se sia rettangolo, acutangolo o ottusangolo.
AB = 3,2 cm
BC = AB+2,2
AC = BC-0,9
2p=? Tipo di triangolo?
BC = AB+2,2 = 3,2+2,2 = 5,4 cm
AC = BC-0,9 = 5,4-0,9 = 4,5 cm
2p = AB+BC+AC = 3,2+5,4+4,5 = 13,1 cm
Si tratta di un triangolo acutangolo.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo un lato misura 1,5 cm e gli altri due
sono rispettivamente i 4/3 e i 5/3 del primo lato.
Calcola il perimetro del triangolo dato.
BC = 4/3 AB = 1,5/3*4 = 0,5*4 = 2 cm
AC = 5/3 AB = 1,5/3*5 = 0,5*5 = 2,5 cm
AB = 1,5 cm
BC = 4/3 AB
AC = 5/3 AB
2p = ?
2p = AB+BC+AC = 1,5+2+2,5 = 6 cm
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 6
Il perimetro di un triangolo misura 60 cm. sapendo che la somma di due lati
consecutivi è di 45 cm e che uno di essi è i 4/5 dell'altro, calcola la lunghezza di
ciascuno dei lati.
B|-x-|-x-|-x-|-x-|-x-|C
A|-x-|-x-|-x-|-x-|B
BC = (AB+BC)/(5+4)*5 = 45/9*5 = 5*5 = 25 cm
AB = 4/5 BC = 25/5*4 = 5*4 = 20 cm
AC = 2p - (AB+BC) = 60-45 = 15 cm
2p = 60 cm
AB+BC = 45 cm
AB = 4/5 BC
Misura lati = ?
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Calcola l'ampiezza dell'angolo in A di un triangolo ABC sapendo che l'angolo in B
misura 44° e che il terzo angolo è il triplo dell'angolo in B?
Essendo A^+B^+C^ = 180° per tutti i triangoli…
C^ = 3*B^ = 3* 44 = 132°
A^
= 180° - (B^+C^) = 180°-(44°+132°) =
= 180° - 176° = 4°
B^ = 44°
C^ = 3*B^
A^ = ?
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Calcola le ampiezze degli angoli acuti di un triangolo rettangolo sapendo che le loro
misure differiscono di 34°.
B^+C^ = 180°-90° = 90°
C^ = ((B^+C^)-(B^-C^))/2 =(90-34)/2= 56/2 = 28°
B^ = 34°+ C^ = 34°+28° = 62°
A^ = 90°
B^-C^ = 34°
B^ = ?; C^= ?
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC l’angolo in A è doppio dell'angolo in B. Sapendo che la somma
dei due angoli è di 114° (A^+B^=114°), determina l'ampiezza di ciascuno degli
angoli interni del triangolo.
A^ |--x--|
B^ |--x--|--x--|
B^ = 2*A^
A^+B^=114°
A^ = (A^+B^)/(2+1) = 114°/3 = 38°
B^ = 2*A^ = 2*38° = 76°
C^ = 180°-(A^+B^) = 180°-114°=66°
A^ = ?; B^ = ?; C^ = ?
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 7
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Calcola le ampiezze degli angoli di un triangolo ABC sapendo che gli angoli in B e in
C superano l'angolo in A rispettivamente di 12° e di 33°.
A^|---x---|
B^|---x---| +12°
C^|---x---| +33°
B^ = A^+12°
C^ = A^+33°
A^ = ?; B^ = ?; C^ = ?
A^ = (180°-12°-33°)/3 = 135°/3 = 45°
B^ = A^+12° = 45°+12° = 57°
C^ = A^+33° = 45°+33° = 78°
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC il perimetro misura 48 cm ed è i 32/9 del lato AB, la lunghezza
del lato BC supera quella del lato AC di 1,7 cm. Determina la misura dei tre lati del
triangolo dato.
AB = 48/32*9 = 1,5*9 = 13,5 cm
BC+AC = 48-13,5 = 34,5 cm
AC
= ((BC+AC)-(BC+AC))/2 = (34,5-1,7)/2 =
= 32,8/2 = 16,4 cm
BC = AC + 1,7 = 16,4+1,7 = 18,1 cm
2p = 48 cm
2p = 32/9 AB
BC = AC + 1,7 cm
AB = ?; BC = ?; AC = ?
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo rettangolo ABC, rettangolo in A, il
perimetro misura 14,2 cm, il lato AC misura 3 cm e
l’angolo in C è il doppio dell'angolo in B. Determina
l'ampiezza degli angoli interni e la misura
dell'ipotenusa del triangolo dato.
A^ = 90^
C^ = 2*B^
B^ = ?; C^ = ?
2p = 14, 2 cm
AC = 3 cm
Ipotenusa?
Essendo il triangolo rettangolo in A, A^ = 90°
B^+C^ = 90°
B^ = 90°/(2+1) = 90°/3 = 30°
C^ = 90° - B^ = 90° - 30° = 60°
Essendo un triangolo 90°, 60° e 30° si ha
BC = 2*AC = 2*3 = 6 cm
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 8
In un triangolo ABC l'angolo in A supera l'angolo in B
di 20° e l'angolo in C è il doppio dell'angolo in A.
Determina l'ampiezza degli angoli interni del triangolo
dato.
A^ = B^ + 20°
C^ = 2*A^
A^ = ?; B^ = ?; C^ = ?
B^ |--x--|
A^ |--x--| + 20°
C^ |--x--|--x--| + 20° + 20°
B^ = (180° - (20*3))/4 = (180-60)/4 = 120/4 = 30°
A^ = B^ + 20° = 30° + 20° = 50°
C^ = 2*A^ = 2*50° = 100°
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC l'angolo in A misura 64° e
l’angolo B è di 34°. Siano date l’altezza CD relativa al
lato AB e il segmento CE, bisettrice relativa allo
stesso lato. Determina l'ampiezza dell’angolo DCE
formato dall’altezza e dalla bisettrice.
A^ = 64°
B^ = 34°
CD = altezza
CD = bisettrice
DCE^ = ?
Essendo A^+B^+C^ = 180° e ADC^ = 90°
C^ = 180°-(A^+B^) = 180-(64+34) = 180-98 = 82°
C^/2 = 82°/2 = 41°
CEB^ = 180°-(C^/2+A^) =180-(41+34)=180-75 = 105°
AEC^ = 180°-CEB^ = 180-105 = 75°
DCE^ = 180-(90°+AEC^)=180-(90+75)=180-165 = 15°
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC l'angolo in A misura 106° e l’angolo in
B è di 48°. Calcola l’ampiezza degli angoli che l’altezza BH
forma con i lati BA e BC.
C^ = 180 – (A^+C^) = 180-(106+48) = 180-154 = 26°
HAC^ = 180 – 106 = 74°
HCA^ = 180 – (90+ HAC^) = 180-(90+74) = 180-164 =
26°
HCB^ = HCA^+ C^ = 26+26 = 52°
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
In un triangolo ABC l'angolo in A misura 60° e l’angolo in
B è i ¾ dell’angolo in A. Calcola l’ampiezza del terzo
angolo del triangolo. Di che triangolo si tratta?
A^ = 60°
B^ = ¾ A^
C^ = ?
B^ = ¾ A^ = 60/4*3 = 15*3 = 45°
C^ = 180 – (A^+B^) = 180-(60+45) = 180-105 = 75°
E’ un triangolo acutangolo
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 9
Un triangolo equilatero è formato da quattro triangoli equilateri
opportunamente organizzati su due file. Sapendo che il
perimetro di uno dei triangoli equilateri è di 15 cm, calcola la
misura di ciascun lato e del perimetro del triangolo dato.
2𝑝𝑡𝑟𝑖𝑎𝑛𝑔𝑜𝑙𝑜𝑒𝑞 = 15 𝑐𝑚
misura dei lati = ?
2p = ?
2𝑝𝑡𝑟𝑖𝑎𝑛𝑔𝑜𝑙𝑜
15
=
= 5 𝑐𝑚
3
3
𝑙2 = 3𝑙1 = 2 ∙ 5 = 10 𝑐𝑚
2𝑝 = 3𝑙2 = 3 ∙ 10 = 30 𝑐𝑚
𝑙1 =
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Un triangolo equilatero è formato da nove triangoli equilateri
opportunamente organizzati su tre file. Sapendo che il perimetro
di uno dei triangoli equilateri è di 15 cm, calcola la misura di
ciascun lato e del perimetro del triangolo dato.
2𝑝𝑡𝑟𝑖𝑎𝑛𝑔𝑜𝑙𝑜𝑒𝑞 = 15 𝑐𝑚
misura dei lati = ?
2p = ?
2𝑝𝑡𝑟𝑖𝑎𝑛𝑔𝑜𝑙𝑜
15
=
= 5 𝑐𝑚
3
3
𝑙2 = 3𝑙1 = 3 ∙ 5 = 15 𝑐𝑚
2𝑝 = 3𝑙2 = 3 ∙ 15 = 45 𝑐𝑚
𝑙1 =
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.
Triangoli - 10
Keywords
Geometria, Geometria piana, Triangolo, Triangolo isoscele, Triangolo
rettangolo, Triangoli, Problemi di geometria con soluzioni
Geometry, Triangle, Triangles, triangle equilateral, triangle isosceles,
triangle scalene, Geometry Problems with Solutions
Geometría, triángulos, triángulo, equilátero, isósceles, escaleno, Área figures
planes
Géométrie, Triangle, Isocèle, équilatéral, scalène, Superficie
Geometrie, Umfang, Triangel, Dreieck, spitzwinkliges Dreieck, rechtwinkliges
Dreieck, stumpfwinkliges Dreieck, Satz des Pythagoras, Mathematik
Copyright© 1987-2010 owned by Ubaldo Pernigo, please contact: [email protected]
Tutti i contenuti, ove non diversamente indicato, sono coperti da licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 3.0 Italia License:
http://creativecommons.org/licenses/by-nc-nd/3.0 (Attribution-Noncommercial-No Derivative Works 3.0) La riproduzione di tutto o parte dei contenuti potranno avvenire solo
senza alcun scopo di lucro e dovranno riportare l’attribuzione all’autore ed un link a UbiMath e/o a quella dell’autore/i originario.