Teoria dei circuiti – Esercitazione di Laboratorio
Transitori e dominio dei fasori
Esercizio 1
T
V0
T
R1
R2
+
−
V0
C V
C
R1
R2
+
−
(a)
C V
C
(b)
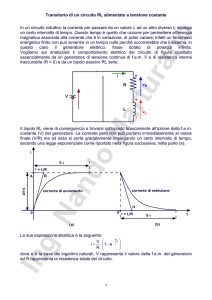
Con riferimento al circuito di figura, si assumano i seguenti valori:
R1 = R2 = 1 kΩ, C = 0.1 µF, V0 = 5 V.
Determinare l’andamento della tensione VC (t) nei due casi seguenti:
• per t < t0 = 0 s l’interruttore T è aperto ed il circuito è a regime. All’istante t = t0
l’interruttore T si chiude;
• per t < t0 = 0 s l’interruttore T è chiuso ed il circuito è a regime. All’istante t = t0
l’interruttore T si apre.
Soluzione
Si analizzino separatamente i due transitori, cominciando dal primo richiesto, ovvero quello
in cui l’interruttore commuta da aperto a chiuso.
R1
IR2
R2
IC=0
V0
C V
C0
R2
+
−
(a)
C V
C
(b)
Per t < t0 = 0 s l’interruttore T è aperto ed il circuito corrisponde a quello indicato con
(a). Dall’ipotesi che la capacità sia a regime, ovvero IC = 0, si ha che IR2 = 0 e quindi
VC0 = VR2 = R2 IR2 = 0 V.
All’istante t = 0 l’interruttore si chiude, ed il circuito si modifica come indicato in (b).
Calcolando il circuito equivalente di Thevenin del circuito formato da V0 , R1 e R2 , si può
considerare il transitorio sul seguente circuito equivalente
R(eq)
V(eq)
C V
C
+
−
con
R1 R2
R2
V0 = 2.5 V, R(eq) =
= 500 Ω
R1 + R2
R1 + R2
e quindi la tensione VC (t) si può esprimere come
V (eq) =
{
VC (t) =
VC0 = 0 V
(
)
V (eq) + VC0 − V (eq) e
−
t
R(eq) C
1
(
= 2.5 1 − e
)
−20 000 t
t ≤ 0s
V t > 0s
come rappresentato nella figura seguente. La costante di tempo del transitorio vale τ =
R(eq) C = 50 µs. Poiché secondo le convenzioni dei segni adottate, la tensione ai capi del condensatore (e quindi anche la quantità di carica in esso accumulata) aumenta, si indichi questo
transitorio come “transitorio di carica”.
2.5
2
50 µs
Vc [V]
1.5
1.58 V
1
0.5
0
0
50
100
t [µs]
150
200
Si passi ora a considerare il secondo transitorio richiesto dall’esercizio. In questo caso il
circuito, rispettivamente per t < t0 e per t > t0 , risulta equivalente ai due circuiti indicati con
(a) e con (b).
IR1 R1
IR2
V0
R2
+
−
IC=0
C V
C
R2
(a)
C V
C0
(b)
Per t < t0 , si calcoli la soluzione di regime assumendo IC = 0, ovvero IR1 = IR2 . Per t > t0
il circuito connesso alla capacità risulta essere la sola R2 ; il suo equivalente di Thevenin è quindi
R2 stessa.
VC0 =
R2
V0 = 2.5 V,
R1 + R2
V (eq) = 0 V,
R(eq) = R2 = 1000 Ω
e la VC (t) si può esprimere come
{
VC (t) =
VC0 = 2.5 V
(
)
V (eq) + VC0 − V (eq) e
−
t
R(eq) C
t ≤ 0s
= 2.5 e−10 000 t V t > 0 s
come rappresentato nella figura seguente. La costante di tempo del transitorio vale τ =
R(eq) C = 100 µs, ovvero è doppia rispetto al caso precedente. Poiché tensione (e quindi anche
carica) della capacità diminuisce fino a zero, si indichi questa fase come “transitorio di scarica”.
Si noti che per via delle differenti costanti di tempo questo transitorio risulta più lento del
precedente.
2
2.5
1.5
100 µs
1
0.92 V
Vc [V]
2
0.5
0
0
100
200
t [µs]
300
400
Realizzazione pratica
Si utilizzino le due resistenze da 1 kΩ, il condensatore da 0.1 µF ed il pulsante. Le resistenze
da 1 kΩ sono contrassegnate dalle tre fasce colorate marrone/nero/rosso; il condensatore da
0.1 µF reca scritto 0.1 oppure 100n. Per quanto riguarda l’interruttore, può essere sostituito
dal pulsante. Il pulsante premuto è equivalente all’interruttore chiuso, il pulsante non premuto
all’interruttore aperto.
Si imposti sull’alimentatore una tensione stabilizzata pari a 5 V. Si imposti inoltre l’oscilloscopio come segue:
• Canale 1 attivo con sensibilità pari a 0.5 V/div o 1 V/div. Per collegare la sonda alla
capacità C, si consiglia di usare un filo metallico, collegandone un capo alla breadboard
e l’altro capo alla sonda (è anche possibile collegare la sonda direttamente alla resistenza
R2 essendo C ed R2 in parallelo, ma stando attenti che eventuali movimenti della sonda
non facciano uscire la resistenza dalla breadboard) .
• Canale 2 disattivato.
• Base dei tempi (per il momento) ininfluente.
• Trigger su “Auto”.
A pulsante aperto, sullo schermo dell’oscilloscopio si dovrebbe vedere una riga continua, la cui
posizione sullo schermo dovrebbe corrispondere al livello 0 V. Premendo il pulsante la tensione,
dopo un breve transitorio, dovrebbe assestarsi ad un livello pari a 2.5 V.
Sebbene entrambi i transitori (sia di carica che di scarica) siano visualizzati sullo schermo
ogni volta che si preme o si rilascia il pulsante, la loro durata è cosı̀ breve da non poter essere
visti ad occhio. Per poterli visualizzare e quindi misurare, è necessario cambiare le impostazioni
dell’oscilloscopio in modo che “congeli” sullo schermo l’istante in cui avviene un transitorio.
Per visualizzare e congelare il solo transitorio di carica, si imposti l’oscilloscopio come segue:
• Base dei tempi a 20 µs/div o 50 µs/div.
• Trigger impostato sul Canale 1 in modalità “Normal”. In questa modalità lo strumento
aggiorna lo schermo solo quando rileva che la tensione del Canale 1 ha un transitorio di
salita o di discesa in cui la tensione attraversa la soglia impostata. Si controlli che il tipo
di transitorio su cui l’oscilloscopio si sincronizzi sia “positivo” (ovvero un transitorio con
tensione crescente), e si fissi la soglia ad un valore tra gli 0.5 V e 1 V. Si consiglia questo
range di valori per avere una tensione di soglia abbastanza lontana dagli 0 V della soluzione
di regime con interruttore aperto (e quindi evitare che l’oscilloscopio aggiorni lo schermo
solo per via del rumore sul Canale), ma abbastanza bassa da avere una transizione di
tensione sufficientemente ripida.
3
In questo modo lo schermo dell’oscilloscopio si dovrebbe aggiornare ogni volta che l’interruttore
si chiude, ovvero quando viene premuto il pulsante, fissando una immagine simile alla seguente.
Si provi ora a misurare, tramite i cursori dell’oscilloscopio, la costante di tempo del transitorio. Per fare questo, il metodo più semplice è il seguente. Si supponga che la tensione vari
esattamente tra 0 V e 2.5 V, ovvero ∆V = 2.5 V (per una misura più precisa, si può misurare
con esattezza il ∆V con il trigger in modalità “Auto” oppure aumentando la scala temporale
dello schermo). Dall’analisi teorica, dopo un tempo pari alla costante di tempo τ , il valore della
tensione VC dovrebbe valere
(
)
VC (τ ) = ∆V 1 − e−1 = 1.58 V
Si imposti il primo cursore (cursore di riferimento) nel punto in cui il transitorio di carica
comincia, ed il secondo nel punto in cui la tensione è uguale a 1.58 V. Il ∆t tra i due cursori è
la misura della costante di tempo τ del transitorio.
NOTA: per via della tolleranza dei componenti (il valore delle resistenze viene assicurato
essere entro il 5% del valore nominale, mentre per le capacità la tolleranza è normalmente del
10%), è normale attendersi un valore simile, ma non perfettamente coincidente con quello atteso.
Per congelare sullo schermo l’istante in cui avviene il transitorio di scarica di C, ovvero
il transitorio che si ha quando si rilascia il pulsante, è sufficiente cambiare le impostazioni
dell’oscilloscopio agendo sulla programmazione del trigger.
• Trigger impostato sul Canale 1 in modalità “Normal”, eventualmente cambiare la soglia
del trigger con un valore prossimo a 2.5 V (si consiglia tra 1.5 V e 2 V per gli stessi motivi
spiegati in precedenza). Si imposti questa volta il fronte del trigger di tipo “negativo”.
• Base dei tempi a 50 µs/div o 100 µs/div, per compensare l’atteso aumento della costante
di tempo.
4
Lo schermo dell’oscilloscopio dovrebbe essere simile al seguente.
Come nel caso precedente, si provi a calcolare la costante di tempo del transitorio. Dopo un
tempo τ dall’inizio del transitorio, la tensione è eguale a
VC (τ ) = ∆V e−1 = 0.92 V
dove si è assunto ∆V = 2.5 V. Si misuri tramite i cursori dello strumento la differenza di tempo
tra l’inizio del transitorio e l istante in cui VC vale 0.92 V. Questo tempo dovrebbe valere attorno
ai 100 µs.
Esercizio 2 (facoltativo)
T
V0
R1
R2
+
−
T
L
V0
C V
C
(a)
R1
L
R2
+
−
C V
C
(b)
Con riferimento al circuito di figura, si assumano i seguenti valori:
R1 = R2 = 1 kΩ, C = 0.1 µF, L = 0.5 µH, V0 = 5 V. Si supponga che per t < t0 = 0 sec il
circuito sia a regime.
Si determini:
• l’andamento della tensione VC (t) supponendo sia che per t = t0 l’interruttore si chiuda
(caso (a) in figura) sia che allo stesso istante si apra (caso (b));
• per quali di valori di R1 ed R2 (supponendo R1 = R2 ) la tensione VC (t) ha un transitorio
di tipo sottosmorzato.
5
Soluzione
Si consideri il primo punto dell’esercizio, analizzando separatamente i due transitori cominciando da quello in cui l’interruttore commuta da aperto a chiuso.
VL=0
IL0
R1
IR2
L
R2
L
IC=0
V0
C V
C0
R2
+
−
(a)
C V
C
(b)
Per t < t0 = 0 s l’interruttore T è aperto ed il circuito corrisponde a quello indicato con (a).
Dall’ipotesi che sia la capacità sia a regime, ovvero IC = 0, sia l’induttore sia a regime, ovvero
VL = 0, si ha che IR2 = 0 e quindi VC0 = VR2 = R2 IR2 = 0 V e che IL0 = IC = 0 A.
All’istante t = 0 l’interruttore si chiude, ed il circuito si modifica come indicato in (b).
Calcolando il circuito equivalente di Thevenin del circuito formato da V0 , R1 e R2 si ha
V (eq) =
R2
V0 = 2.5 V,
R1 + R2
R(eq) =
R1 R2
= 500 Ω
R1 + R2
e la tensione VC (t) può essere espressa considerando il circuito equivalente
R(eq)
L
V(eq)
C V
C
+
−
che ha un transitorio del secondo ordine, dove la frequenza naturale ed il coefficiente di smorzamento valgono
1
ωN = √
≃ 141.4 krad/sec
LC
R(eq)
ζ=
2
√
√
C
1 R1 R2
=
L
2 R1 + R2
C
= 3.536
L
Il transitorio è dunque sovrasmorzato, e può essere espresso tramite:
σ1 = ζωN − ωN
√
ζ 2 − 1 ≃ 20.4 ks−1
√
σ2 = ζωN + ωN
VC0
(eq)
VC (t) =
V
ζ 2 − 1 ≃ 979.6 ks−1
t ≤ t0
)
σ2
IL0
−σ
t
+
e 1+
+ VC0 − V
σ2 − σ1 C (σ2 − σ1 )
((
)
)
σ1
IL0
(eq)
+ VC0 − V
+
e−σ2 t t > t0
σ2 − σ1 C (σ2 − σ1 )
((
(eq)
)
Poiché σ2 ≫ σ1 , tale transitorio si può approssimare con
{
VC (t) ≃
VC0
t ≤ t0
)
(
−σ
t
(eq)
1
t > t0
1−e
V
ovvero è del tutto simile al precedente transitorio di carica del primo ordine che abbia τ ≃
1/σ1 ≃ 49 µs, come si può osservare dalla figura seguente.
6
2.5
2
Vc [V]
1.5
1
0.5
0
0
50
100
150
t [µs]
200
250
300
Per quanto riguarda il transitorio di scarica, si considerino i seguenti circuiti.
VL=0
IR1 R1
V0
IL0
IR2
L
IC=0
L
R2
+
−
C V
C0
R2
(a)
C V
C
(b)
Per t < t0 = 0 s il circuito da considerare è quello indicato con (a), con l’ipotesi che sia la
capacità sia a regime (ovvero IC = 0) sia l’induttore sia a regime (ovvero VL = 0) da cui si ha
VC0 =
R1
V0 = 2.5 V,
R1 + R2
IL0 = IC0 = 0 A
mentre per il tempo di carica si calcoli il circuito equivalente di Thevenin della resistenza R2 ,
corrispondente a
V (eq) = 0 V,
R(eq) = R2 = 1 kΩ
da cui si possono ricavare in modo analogo al precedente i parametri del transitorio.
1
≃ 141.4 krad/sec
ωN = √
LC
R(eq)
ζ=
2
√
√
C
R2
=
L
2
C
= 7.07
L
Anche il transitorio di scarica è sottosmorzato, con
σ1 = ζωN − ωN
√
√
σ2 = ζωN + ωN
ζ 2 − 1 ≃ 10.05 ks−1
ζ 2 − 1 ≃ 1989.9 ks−1
ed il suo andamento, del tutto simile come nel caso precedente ad un transitorio del primo
ordine in cui τ ≃ 1/σ1 ≃ 99.5 µs, si può osservare nella figura seguente.
7
2.5
Vc [V]
2
1.5
1
0.5
0
0
100
200
300
t [µs]
400
500
600
Si consideri ora il secondo punto dell’esercizio, ove si chiede di cambiare le due resistenze
R1 ed R2 in modo da avere un transitorio sottosmorzato. La condizione per cui un transitorio
del secondo ordine è sottosmorzato è 0 < ζ < 1, ovvero
√
L
≃ 141.4 Ω
C
0 < R(eq) < 2
Se si considerano R1 = R2 , ed i valori di R(eq) trovati nei transitori di carica e di scarica, il
valore limite di R1 e R2 per cui si ha un transitorio di carica sottosmorzato è
R1 = R2 < 282.8 Ω
mentre il valore limite per cui anche il transitorio di scarica è
R1 = R2 < 141.4 Ω
Si consideri come esempio il transitorio di carica dove R1 = R2 = 100 Ω. In questo caso i
due parametri sono
ωN =≃ 141.4 krad/sec, ζ = 0.353
e, ponendo
σ0 = ωN ζ = 50 ks−1 ,
√
ω0 = ωN
1 − ζ 2 = 132.3 krad/s
il transitorio è del tipo
VC (t) = V
(eq)
+e
−σ0 t
((
)
))
(
)
IL0
σ0 (
(eq)
(eq)
sin ω0 t + VC0 − V
cos ω0 t
+
VC0 − V
ω0 C
ω0
ed è rappresentato nella figura seguente.
3.5
3
Vc [V]
2.5
2
1.5
23.7 µs
1
0.5
0
0
25
50
t [µs]
8
75
100
Per quanto riguarda il transitorio di scarica, si ha
ωN =≃ 141.4 krad/sec,
da cui
σ0 = ωN ζ = 100 ks−1 ,
ζ = 0.707
√
ω0 = ωN
1 − ζ 2 = 100 krad/s
e l’andamento del transitorio è rappresentato nella figura seguente. Si noti che, essendo ζ più
prossimo al valore limite ζ = 1 rispetto al caso precedente, la sovraelongazione risulta meno
marcata.
2.5
2
Vc [V]
1.5
1
0.5
0
-0.5
0
25
50
t [µs]
75
100
Realizzazione pratica
Si implementi il caso più interessante, ovvero il transitorio di carica e scarica sottosmorzato
con R1 = R2 = 100 Ω. La realizzazione e le impostazioni degli strumenti per questo esercizio
sono in tutto simili a quelle del caso precedente, all’infuori della scala dei tempi dell’oscilloscopio,
che conviene diminuire leggermente per meglio visualizzare i due transitori Si ricorda che le due
resistenze da 100 Ω sono contrassegnate dalle tre fasce colorate marrone/nero/marrone.
I due transitori, rispettivamente di carica e scarica, dovrebbero apparire simili a quelli in
figura.
Effettuare misure del tempo di carica e scarica risulta abbastanza complesso. Interessante
risulta invece, nel caso del transitorio di carica (in quanto le oscillazioni sono più marcate),
misurare la frequenza di auto-oscillazione ω0 , misurando la distanza tra due picchi (i primi tre
sono chiaramente visibili sullo schermo) nel transitorio di tensione. Si misuri attraverso i cursori
dell’oscilloscopio la distanza (in tempo) tra il primo picco positivo ed il primo picco positivo,
equivalente a metà del periodo di oscillazione. Questo tempo dovrebbe risultare pari a
T
2π
=
≃ 23.75 µs
2
2ω0
9
Esercizio 3
C1
R1
V0 +
Z1
R2
C2
VC2
V0 +
-
Z2 VZ2
-
(a)
(b)
Con riferimento ai due circuiti rappresentati in figura, si assumano i seguenti valori:
f0 = 1000 Hz, R1 = 1 kΩ, C1 = 0.1 µF, R2 = 1 kΩ, C2 = 0.1 µF, V0 (t) = 1 · cos (2πf0 t) V.
• Calcolare l’andamento della tensione VC2 (t) nel caso in figura (a). Si indichi se la tensione sinusoidale trovata sia in anticipo, in ritardo, oppure in fase, rispetto alla tensione
sinusoidale imposta V0 ;
• Il circuito in (b) è una generalizzazione del circuito (a), dove alla serie di R1 e C1 è
stato sostituito una generico bipolo Z1 , ed al parallelo si R2 e C2 un generico bipolo
Z2 . Si supponga di poter cambiare arbitrariamente Z1 e Z2 , ma di doverli realizzare
esclusivamente tramite serie oppure parallelo di una resistenza del valore di 1 kΩ e di una
capacità da 0.1 µF. Si determini quando la tensione sinusoidale VZ2 è in fase, quando in
anticipo e quando in ritardo rispetto a V0 .
Soluzione
Essendo V0 un generatore sinusoidale, conviene risolvere il circuito (come del resto già suggerito dal punto (b)) nel dominio dei fasori. Si consideri quindi per la soluzione di entrambi i
punti il circuito indicato al punto (b)
Z1
V0 +
Z2 VZ2
-
in cui è immediato calcolare che
Z2
Ṽ0
Z1 + Z2
Per il primo punto dell’esercizio, si ha che l’impedenza Z1 è data dalla serie tra le impedenze
associate a R1 e C1 e Z2 dal parallelo tra le impedenze associate a R2 e C2 , tutte calcolate ad
una frequenza pari a f0 = 1 kHz, ovvero una frequenza angolare ω0 = 6.28 krad/s. La tensione
VC2 richiesta può essere calcolata mediante la VZ2 .
ṼZ2 =
Z1 = R 1 +
Z2 =
1
R2 jωC
2
R2 +
1
jωC2
=
1
1
= R1 − j
≃ 1 kΩ − j 1.59 kΩ
jωC1
ωC1
1
ωR2 C2
R2
= R2
− jR2
≃ 717 Ω − j 450 Ω
2
1 + jωR2 C2
1 + (ωR2 C2 )
1 + (ωR2 C2 )2
In entrambi i casi, la parte immaginaria dell’impedenza equivalente è sempre negativa. Inoltre
si consideri Ṽ0 = 1 V.
La soluzione cercata è data da
ṼZ2 =
Z2
717 − j 450
Ṽ0 ≃
V ≃0.302 V + j0.097 V ≃ 0.302 ej 0.31
Z1 + Z2
1720 − j 2040
10
che riscritta come funzione sinusoidale
VC2 (t) = VZ2 (t) ≃ 0.302 cos (2πf0 t + 0.31) V
ovvero risulta in anticipo approssimativamente di φ0 ≃ 0.31 rad rispetto a V0 (t). Poiché un
ritardo di fase pari a 2π rad corrisponde ad un periodo, ovvero un tempo T = 1 ms ad una
frequenza di 1 kHz, l’anticipo corrisponde a
τ0 =
φ0
T ≃ 49.3 µs
2π
Le due tensioni V0 (t) e VC2 (t) sono rappresentate nella figura seguente.
V0(t)
VC2(t)
1.5
49.3 µs
Vc [V]
1
0.5
0
-0.5
-1
0
0.5
1
1.5
t [ms]
Poiché nel circuito del primo punto si osserva già un anticipo di fase, si cerchi, risolvendo il
secondo punto dell’esercizio, un circuito che ottenga un ritardo di fase, ed un uno in cui le due
tensioni risultino perfettamente in fase. Il vincolo richiesto dall’esercizio può essere interpretato
come la richiesta che Z1 e Z2 possano solo realizzate tramite serie o parallelo, rispettivamente,
di R1 e C1 e di R2 e C2 . L’impedenza Zs della connessione serie e quella Zp della connessione
parallelo sono stati calcolati al punto precedente, ovvero:
Zs ≃ 1 kΩ − j 1.59 kΩ
Zp ≃ 717 Ω − j 450 Ω
Tralasciando la configurazione del punto uno, possono esistere solo tre differenti configurazioni, ovvero Z1 = Z2 = Zp , Z1 = Z2 = Zs e Z1 = Zp , Z2 = Zs .
Sebbene sia possibile risolvere il problema da un punto di vista strettamente teorico, si
considerino per semplicità questi tre casi (indicati in figura con (a), (b) e (c)) separatamente.
C1
C1
R1
C1
R1
R1
V0 +
R2 C V
2
Z2
V0 +
R2
-
C2
(a)
VZ2
V0 +
R2
-
C2
(b)
• nel caso (a) sia Z1 che Z2 sono realizzati tramite un parallelo
ṼZ2 =
Z2
Zp
1
Ṽ0 =
Ṽ0 = Ṽ0
Z1 + Z2
Zp + Zp
2
ovvero VZ2 (t) = 0.5 cos (2πf0 t). Tale tensione è in fase con V0 (t).
11
(c)
VZ2
• nel caso (b) sia Z1 che Z2 sono realizzati tramite una serie
ṼZ2 =
Z2
Zs
1
Ṽ0 =
Ṽ0 = Ṽ0
Z1 + Z2
Zs + Zs
2
ovvero VZ2 (t) = 0.5 cos (2πf0 t). Come nel caso precedente, tale tensione è in fase con
V0 (t).
• nel caso (c) si ha Z1 = Zp ≃ 717 Ω − j 450 Ω e Z2 = Zs ≃ 1 kΩ − j 1.59 kΩ. In questo caso
ṼZ2 =
Z2
Zs
Ṽ0 =
Ṽ0 ≃ 0.698 V − j 0.097 V ≃ 0.705 e−j 0.138 V
Z1 + Z2
Zp + Zs
ovvero VZ2 (t) ≃ 0.705 cos (2πf0 t − 0.138). Si ha quindi un ritardo di fase pari a φ0 =
0.138 rad, che per f0 = 1 kHz corrispondono ad un tempo pari a
τ0 =
φ0
T ≃ 22 µs
2π
L’andamento della VZ2 (t) nei casi (a) e (c) è rappresentato nelle due figure seguenti.
Caso (a)
Caso (c)
V0(t)
VC2(t)
1.5
1
1
0.5
0.5
Vc [V]
Vc [V]
1.5
0
0
-0.5
-0.5
-1
-1
0
0.5
1
V0(t)
VC2(t)
22 µs
1.5
0
t [ms]
0.5
1
1.5
t [ms]
Realizzazione pratica
Si utilizzino due resistenze da 1 kΩ e due condensatori da 0.1 µF. Si utilizzi il generatore di
funzioni per generare V0 (t), impostando un’onda sinusoidale di 1 kHz, con una ampiezza di 1 V
(ovvero il cui picco positivo raggiunge 1 V e il picco negativo raggiunge −1 V.) Per via della
bassa precisione del generatore di funzioni, si consiglia di controllare sia il valore dell’ampiezza
che quello della frequenza tramite l’oscilloscopio, collegando la sonda del Canale 1 direttamente
al generatore di funzioni. Le impostazioni consigliate per l’oscilloscopio sono le seguenti.
• Canale 1 con sensibilità pari a 0.1 V/div o 0.5 V/div
• Base dei tempi a 200 µs/div o 500 µs/div.
• Trigger in “Auto” oppure “Normal”. Sebbene non sia influente per l’esercizio, si consiglia
di impostare il tipo di fronte su positivo e una tensione di soglia a 0 V (dipendentemente
dall oscilloscopio usato, con il trigger impostato su “Auto” il valore di tale soglia potrebbe
essere non regolabile).
Si realizzi ora il circuito chiesto al primo punto dell’esercizio. Scopo di questa esercitazione
è misurare sia l’ampiezza di VZ2 che il suo sfasamento rispetto alla tensione V0 . Per questo si
lasci la sonda del Canale 1 collegata alla V0 mentre si colleghi la sonda del Canale 2 alla Z2 . Si
imposti sul canale 2 la stessa sensibilità impostata sul Canale 1.
12
ATTENZIONE: Le due masse dei due canali dell’oscilloscopio (ovvero i due coccodrilli della
sonda) sono cortocircuitati all interno dell’oscilloscopio. Pertanto è assolutamente NECESSARIO che, quando si utilizza più di un canale, tutte le masse delle sonde siano connesse allo
stesso nodo.
Si usino i cursori dell’oscilloscopio sia per misurare l’ampiezza di VZ2 , sia per misurare
lo sfasamento tra V0 e VZ2 . Per misurare lo sfasamento, si consiglia di misurare la distanza
tra i due istanti di tempo in cui le due sinusoidi passano per gli 0 V. Dipendentemente dalla
scala temporale impostata, questi punti potrebbero risultare molto vicini sullo schermo. Per
aumentare l’accuratezza della misura, è possibile diminuire a piacere la scala temporale. Il
risultato a schermo dovrebbe essere simile al seguente.
Si realizzino ora il caso (a) ed il caso (c) trovati nella seconda parte dell’esercizio. Le
procedure per misurare ampiezza e sfasamento delle due sinusoidi V0 e VZ2 sono per tutto
simili al caso precedente. Le immagini sull’oscilloscopio dovrebbero essere simili ai due esempi
riportati qui sotto.
13