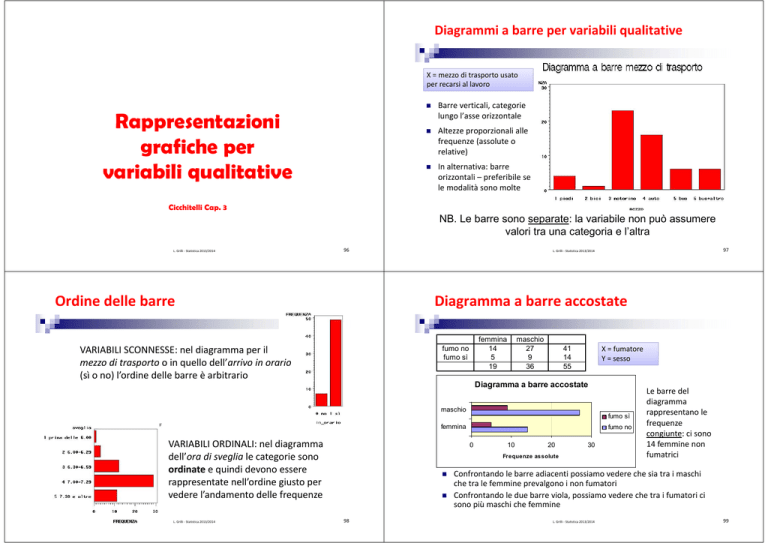
Diagrammi a barre per variabili qualitative
X = mezzo di trasporto usato per recarsi al lavoro
Rappresentazioni
grafiche per
variabili qualitative
Barre verticali, categorie lungo l’asse orizzontale
Altezze proporzionali alle frequenze (assolute o relative)
In alternativa: barre orizzontali – preferibile se le modalità sono molte
Cicchitelli Cap. 3
NB. Le barre sono separate: la variabile non può assumere
valori tra una categoria e l’altra
L. Grilli ‐ Statistica 2013/2014
96
Ordine delle barre
97
L. Grilli ‐ Statistica 2013/2014
Diagramma a barre accostate
VARIABILI SCONNESSE: nel diagramma per il mezzo di trasporto o in quello dell’arrivo in orario
(sì o no) l’ordine delle barre è arbitrario
femmina
14
5
19
fumo no
fumo sì
maschio
27
9
36
X = fumatore
Y = sesso
41
14
55
Diagramma a barre accostate
maschio
fumo sì
femmina
VARIABILI ORDINALI: nel diagramma dell’ora di sveglia le categorie sono ordinate e quindi devono essere rappresentate nell’ordine giusto per vedere l’andamento delle frequenze
L. Grilli ‐ Statistica 2013/2014
fumo no
0
10
20
30
Frequenze assolute
98
Le barre del diagramma rappresentano le frequenze congiunte: ci sono 14 femmine non fumatrici
Confrontando le barre adiacenti possiamo vedere che sia tra i maschi che tra le femmine prevalgono i non fumatori
Confrontando le due barre viola, possiamo vedere che tra i fumatori ci sono più maschi che femmine
L. Grilli ‐ Statistica 2013/2014
99
Diagramma a barre in pila
femmina
14
5
19
fumo no
fumo sì
maschio
27
9
36
Diagramma a barre in pila 100%
41
14
55
femmina
14
5
19
fumo no
fumo sì
Diagramma a barre in pila
femmina
30
0%
40
25%
996
in cerca di 1a occup.
altri
TOTALE
1152
L. Grilli ‐ Statistica 2013/2014
101
Barre o torta?
Tab. 2- Forze lavoro per
condizione, anno 1999 (migliaia)
disoccupati
100%
Per confrontare le proporzioni di fumatori tra i maschi e le femmine, conviene impilare le barre usando le percentuali di colonna anziché le frequenze
Diagramma a torta
Freq.
75%
100
L. Grilli ‐ Statistica 2013/2014
20435
50%
Frequenze relative %
Per capire qual è la proporzione di fumatori tra i maschi e le femmine, conviene impilare le barre occupati
maschio
75.0%
25.0%
100.0%
fumo sì
Frequenze assolute
Condizione
femmina
73.7%
26.3%
100.0%
fumo no
femmina
fumo sì
20
fumo no
fumo sì
maschio
fumo no
10
41
14
55
Diagramma a barre in pila 100%
maschio
0
maschio
27
9
36
Diagramma circolare (torta): angolo al centro proporzionale alla frequenza
Diagramma a barre migliore percezione delle differenze
Diagramma a torta migliore percezione della composizione
596
23179
Occupati
Fonte: Istat, Rapporto
sull'Italia 2001
in cerca di 1a occup.
disoccupati
360
nj
altri
N
L. Grilli ‐ Statistica 2013/2014
0
102
0.2
0.4
0.6
0.8
1
L. Grilli ‐ Statistica 2013/2014
103
http://www.causeweb.org
Un grafico orrendo
Located at http://people.howstuffworks.com/prison4.htm
104
105
Grafici per variabili quantitative
Rappresentazioni
grafiche per variabili
quantitative
Per capire come sintetizzare la distribuzione di un carattere quantitativo è utile conoscere la sua forma
La forma di una distribuzione può essere vista attraverso un grafico
Grafici più utilizzati
● Dot‐plot
● Ramo‐foglia (Steam and leaf)
● Istogramma
● Diagramma a bastoncini
● Box‐plot [verrà presentato più avanti, dopo gli indici di forma]
Cicchitelli Cap. 3
106
L. Grilli ‐ Statistica 2013/2014
107
Diagramma a bastoncini
Dot‐plot
Quando la variabile è discreta con poche modalità
Diagramma a bastoncini: altezza proporzionale alla frequenza
Tab. 3 – Famiglie per numero di
componenti. Italia 1998.
Bar Chart
Componenti
freq.
%
6000000
1
2
3
4
5
6 e più
Totale
4594130
5527810
4954870
4466810
1294420
381960
21220000
21.65
26.05
23.35
21.05
6.1
1.8
100
5000000
Il dot‐plot mostra i singoli casi osservati come punti
dal dot‐plot possiamo vedere la forma, il centro e la dispersione dei dati
4000000
Velocità di alcuni mammiferi
5
15
Il dot-plot è utile quando:
• si hanno pochi casi
• si vogliono vedere i singoli valori
3000000
2000000
25
35
45
55
65
75
velocità (mph)
1000000
Fonte: Istat, Rapporto sull'Italia 2001
Attenzione. Software diversi fanno dot-plot diversi: a volte 1 punto rappresenta 1
singolo caso, a volte 2 o più casi, a volte i valori vengono arrotondati
0
1
2
3
4
5
6 e più
Componenti
108
L. Grilli ‐ Statistica 2013/2014
Dot‐plot: durata gestazione di alcuni mammiferi
Istogramma
La distribuzione è centrata verso i valori più bassi, senza gruppi o buchi particolari
C’è una sorta di ‘muro’ a 0 giorni, perché nessun mammifero può avere un periodo di gestazione più piccolo!
elefante
160
0
100
200
300
400
500
600
700
durata gestazione (giorni)
L. Grilli ‐ Statistica 2013/2014
L’elefante è l’unico mammifero fuori norma (outlier)
Circa la metà dei mammiferi hanno un periodo di gestazione superiore a 160 giorni e la metà hanno un periodo più breve
La metà centrale ha un periodo di gestazione che varia tra i 63 e i 284 giorni.
L. Grilli ‐ Statistica 2013/2014
110
109
L’istogramma rappresenta un insieme di casi (raggruppati in classi) come rettangoli
Se le classi sono di uguale ampiezza, l’altezza del rettangolo è proporzionale alla frequenza della classe (molti programmi di analisi dei dati consentono solo classi di uguale ampiezza)
L’istogramma può essere costruito utilizzando sia le frequenze assolute che relative
Rappresenta la distribuzione sotto la seguente ipotesi: in ogni classe le frequenze sono uniformemente distribuite nell’intervallo
L. Grilli ‐ Statistica 2013/2014
111
Istogramma: esempio (freq. assolute)
Istogramma: esempio (freq. relative) Quale proporzione degli studenti ha un’altezza di 180 cm o più?
Soluzione
Individuare l’intervallo di valori >180 sull’asse X
Quale proporzione dell’area totale corrisponde alle barre su questo intervallo?
10 |- 20
20 |- 30
30 |- 40
40 |- 50
50 |- 60
Frequenza
3
6
5
4
2
Is t o gra m m a : T e m pe ra t ura M a s s im a
G io rna lie ra
7
5
5
4
4
3
3
2
2
1
Il carattere è continuo
non c’è spazio fra le
barre!
6
6
Frequenza
Intervallo
0
0
0
0 0 10 10 2020 30 30 40 40 50 50 60 60 70
Temperatura in Gradi
112
L. Grilli ‐ Statistica 2013/2014
Istogramma: quante classi?
L. Grilli ‐ Statistica 2013/2014
113
L’arte di fare istogrammi
Cambiando l’ampiezza delle classi dell’istogramma (o cambiando il numero di classi) a volte si ha un’impressione diversa della forma della distribuzione
Per esempio, l’istogramma (1) per la velocità dei mammiferi ha meno barre ma più ampie rispetto all’istogramma (2) e mostra una forma a campana più simmetrica, con un solo picco invece di due Se ci sono pochi valori è difficile identificare i picchi, in questi casi è meglio utilizzare grafici che mostrano i singoli dati, come il dot‐plot o il ramo‐foglia
(1)
• A occhio questa proporzione è circa 1/3 circa 1/3 degli studenti hanno un’altezza>180
• In maniera più precisa: possiamo sommare le altezze delle 3 barre dell’istogramma alla destra di 180, cioè 22+6+2 = 30 30%
(2)
Non c’è una regola per trovare qual è l’ampiezza di classe migliore per disegnare l’istogramma, proprio come per un fotografo non c’è una regola che dica quando e come usare lo zoom! Versioni diverse del grafico mettono in luce caratteristiche differenti della distribuzione: l’abilità dello statistico sta nel trovare una versione che mostra bene le caratteristiche più importanti!
Un istogramma è una buona rappresentazione dei dati quando:
Ci sono molti valori da rappresentare
Non interessa conoscere la posizione di ciascun valore
Si è interessati a mostrare la forma generale della distribuzione
L. Grilli ‐ Statistica 2013/2014
114
L. Grilli ‐ Statistica 2013/2014
115
Istogramma: classi di ampiezza diversa
Istogramma: classi di ampiezza diversa (cont)
Altezza = hi = fi / ai = densità classe
xi-1
xi
X
Base = xi – xi-1 = ai = ampiezza classe
Area = ai hi = fi = frequenza classe
Definire classi di ampiezza variabile è utile quando vi sono intervalli con alta frequenza e intervalli con bassa frequenza (es. per la variabile «reddito mensile da lavoro dipendente» molti lavoratori hanno valori tra 1000 e 2000 euro ( è opportuno fare classi di 100 euro), pochi tra 8000 e 10000 ( bastano classi di 500 o 1000 euro)
Classi
Freq.rel.
Ampiezza
Densità
x0- x1
f1
a1
h1
…
…
…
…
xi-1- xi
fi
ai
hi
…
…
…
…
xk-1- xk
fk
ak
hk
Totale
1
Densità di frequenza:
Ampiezza di classe:
116
L. Grilli ‐ Statistica 2013/2014
Istogramma: classi di ampiezza diversa (cont)
hi = fi /ai
ai = xixi-1
L. Grilli ‐ Statistica 2013/2014
117
La funzione di ripartizione
Data una v.s. quantitativa X si dice funzione di ripartizione
F(x) la frequenza relativa (proporzione) dei valori minori o
uguali a x:
Distribuzione dei
redditieri per classi
di reddito dichiarato
in milioni di lire
(Italia, 1977)
F ( x) pr u : X (u ) x pr X x
Proprietà:
• F(x)=0 per x < xmin
• F(x)=1 per x ≥ xmax
• F(x) non decrescente
Insieme delle modalità ordinate di X:
X discreta {xmin,…, xj ,…, xmax }
X continua [xmin, xmax ]
Vediamo 2 tipi di funzione di ripartizione: quella empirica e quella dedotta dall’istogramma
L. Grilli ‐ Statistica 2013/2014
118
L. Grilli ‐ Statistica 2013/2014
119
Funzione di ripartizione empirica
Funzione di ripartizione empirica (cont)
Data una successione di dati grezzi x1, x2, …, xn di
una v.s. X, la F(X) calcolata a partire da tali dati è
detta funzione di ripartizione empirica.
Proprietà:
• F(X<xmin)=0; F(X≥xmax)=1; non decrescente
1
0.875
• Funzione ‘a gradini’: costante in [xj-1; xj)
0.75
X = {0,0,3,5,5,12,15,15}
xj
nj
0
3
5
12
15
tot
fj
F(x)
2
1
2
1
0.250
0.125
0.250
0.125
0.250
0.375
0.625
0.750
2
8
0.250 1.000
1.000
fj
0.625
0.5
0.375
• In X=xj F(x) ‘salta’ di fj (frequenza rel. di xj)
0.25
0.125
0
-1
1
3
5
7
9
11
13
15
17
1
0.875
1
0.875
0.625
0.5
0.75
Pr(y<=5)
Fj
0.75
0.625
f(y=5)
fj
0.5
0.375
0.375
0.25
0.25
0.125
0.125
0
-1
1
3
5
7
9
11
13
15
17
0
-1
1
3
120
L. Grilli ‐ Statistica 2013/2014
Funzione di ripartizione dedotta
dalla densità (variabili continue)
5
7
9
11
13
15
17
121
L. Grilli ‐ Statistica 2013/2014
Funzione di ripartizione dedotta
dalla densità (variabili continue)
Proprietà:
x
pr ( X x) F ( x)
• F(X<xmin)=0; F(X≥xmax)=1; non decrescente
f (t )dt
• Funzione lineare in [xj-1; xj)
Ipotesi dell’istogramma
• la derivata prima rappresenta la pendenza dei segmenti di
retta che uniscono due estremi di classe successivi
F ( x) F ( x j 1 ) h j ( x x j 1 ),
hj
densità
x x j 1 ; x j
1
0.9
fj
Interpolazione lineare
in (xj-1; xj)
0.8
0.7
x j x j 1
0.6
F ( x) F ( x j 1 ) h j ( x x j 1 )
Esatta in xj
0.5
0.4
0.3
0.2
0.1
0
L. Grilli ‐ Statistica 2013/2014
122
0
10
20
30
40
50
60
70
80
L. Grilli ‐ Statistica 2013/2014
90
100
123
Grafici per serie storiche
Cartogrammi
Rappresentazione di serie territoriali
Sottoscrizioni alla rivista per anno
350
250
Aree geografiche: comuni
200
150
Carattere: densità della popolazione
100
50
0
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
Forma della distribuzione: simmetrica
125
L. Grilli ‐ Statistica 2013/2014
Forma della distribuzione: asimmetrica
La forma della distribuzione si dice simmetrica se le osservazioni sono distribuite approssimativamente in modo simmetrico rispetto al centro La forma della distribuzione è detta asimmetrica se le osservazioni sono distribuite in modo marcatamente asimmetrico
Distribuzione con Asimmetria Positiva
Distribuzione Simmetrica
10
9
8
7
6
5
4
3
2
1
0
12
10
Frequenza
Una distribuzione con asimmetria
positiva (obliqua a destra) ha una
coda che si estende a destra, nella
direzione dei valori positivi.
8
6
4
2
0
1
Una distribuzione con asimmetria
negativa (obliqua a sinistra) ha una
coda che si estende a sinistra, nella
direzione dei valori negativi.
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
9
8
9
Distribuzione con Asimmetria Negativa
12
10
Frequenza
1991
1990
124
L. Grilli ‐ Statistica 2013/2014
Frequenza
Migliaia di sottoscrittori
300
8
6
4
2
9
0
1
L. Grilli ‐ Statistica 2013/2014
126
L. Grilli ‐ Statistica 2013/2014
2
3
4
5
6
7
127
L. Grilli ‐ Statistica 2013/2014
128
L. Grilli ‐ Statistica 2013/2014
129
130
L. Grilli ‐ Statistica 2013/2014
131
Grafici ingannevoli
Come insegna il classico libro di D. Huff «Mentire con la statistica» il grafici possono essere disegnati in modo da trarre in inganno
I due trucchi più frequenti sono
Compressione o espansione degli assi del diagramma cartesiano
L’asse verticale che non parte da zero
A volte invece i grafici sono semplicemente inutili perché non aggiungono niente ad una sintesi in forma di tabella (tali grafici spesso hanno il fine di catturare l’attenzione del lettore)
L. Grilli ‐ Statistica 2013/2014
Un grafico inutile
Delitti denunciati per criminalità violenta nel 1998 su 100.000
abitanti dai 14 anni in su (fonte: ISTAT)
Due grafici a barre per gli stessi dati: nel primo l’asse verticale parte da zero, nel secondo parte da 180
250
200
150
100
50
0
Bari
Bologna
Milano
Torino
Delitti denunciati per crim inalità violenta nel 1998 su 100.000
abitanti dai 14 anni in su (fonte: ISTAT)
230
220
210
200
190
180
Bari
Bologna
Milano
Qui l’asse verticale non parte da zero: sembra che il tasso di denunce a Torino sia oltre il doppio che a Milano, mentre Bari appare un oasi di tranquillità!
Fonte: adattato da S. Watterson: “Liquid Gold-Australians Are Changing the World of Wine. Even
the French Seem Grateful”, Time, 22 novembre 1999, 68.
Torino
L. Grilli ‐ Statistica 2013/2014
132
L. Grilli ‐ Statistica 2013/2014
133












