CENTRO DI MASSA E MOMENTO D'INERZIA
LA LEZIONE
Il centro di massa
Un oggetto lanciato in prossimità della superficie terrestre con una velocità v è
descritto dalla composizione di due movimenti: un moto rettilineo uniforme orizzontale
(se la resistenza dell’aria è trascurabile) con velocità costante v x e un moto
uniformemente accelerato di caduta determinato dall’accelerazione di gravità g con
velocità iniziale vy. La parabola risultante nel piano delle coordinate cartesiane è quella
propria di un corpo dotato di massa, le cui dimensioni si possono trascurare, su cui
agisce solo la forza gravitazionale.
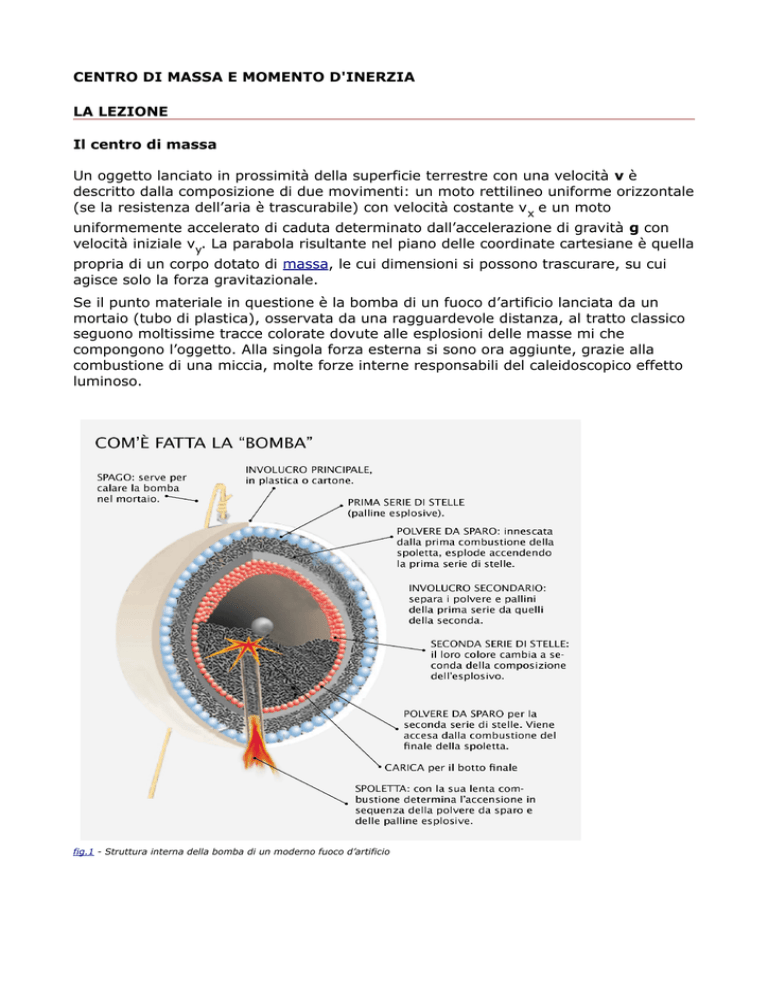
Se il punto materiale in questione è la bomba di un fuoco d’artificio lanciata da un
mortaio (tubo di plastica), osservata da una ragguardevole distanza, al tratto classico
seguono moltissime tracce colorate dovute alle esplosioni delle masse mi che
compongono l’oggetto. Alla singola forza esterna si sono ora aggiunte, grazie alla
combustione di una miccia, molte forze interne responsabili del caleidoscopico effetto
luminoso.
fig.1 - Struttura interna della bomba di un moderno fuoco d’artificio
È possibile passare dalla dinamica del punto
materiale a quella di un insieme di punti
ammettendo che la somma delle forze interne
sia uguale a zero. Allora il moto collettivo delle
particelle è descritto dal centro di massa del
sistema. Questa entità geometrica astratta è
definita attraverso le posizioni e le masse di n
punti.
fig.2 - Uno spettacolo pirotecnico
Fissato un riferimento cartesiano e individuate le masse tramite i vettori ri, la
coordinata x del vettore rcm è semplicemente calcolata come la media pesata delle
coordinate cartesiane xi delle particelle, così per ogni direzione. Ne segue che:
rcm=Σ mi ri/ Σ mi= Σ mi ri/M
fig.3 - Il centro di massa di un insieme di punti materiali
Le altre grandezze cinematiche del sistema sono facilmente individuabili. La quantità
di moto totale del centro di massa pcm= Σ mi vi è uguale a Mvcm mentre
l’accelerazione vale: acm= Σ Fest/M (la somma delle forze interne è zero).
La dinamica di un sistema composto da n particelle può essere generalizzata a sistemi
continui. Nel caso del corpo umano, in una postura tipica della camminata, il centro di
massa è in prossimità dell’ombelico, con oscillazioni di pochi centimetri. Durante un
esercizio di piegamento il punto in questione può trovarsi anche al di fuori del corpo.
fig.4 - La posizione del centro di massa al variare della postura; fig.5 - Fotografia multipla di un salto in lungo
Durante il salto di un atleta, come per il moto di un proiettile, il centro di massa
descrive una parabola, indipendentemente dai complessi movimenti degli arti e del
tronco finalizzati al conseguimento del migliore risultato possibile. Così anche in
esibizioni acrobatiche in cui si utilizzano mezzi molto più veloci del corpo per staccarsi
dal suolo alla velocità vcm, la curva descritta dal centro di massa del sistema è
indisturbata dalle piroette eseguite dal saltatore, mentre singoli punti del sistema (a
esempio la testa del guidatore) possono ruotare intorno al centro di massa.
fig.6 - Fotografia multipla della parabola descritta in un salto spettacolare dal centro di massa del sistema motocicletta-pilota
Nel ballo è in alcuni sport la possibilità di modificare il baricentro semplicemente
distribuendo le masse in modo diverso permette di interpretare salti spettacolari in cui
la testa libra alla stessa altezza del corpo per una brevissima frazione di secondo,
sufficiente comunque per far percepire al pubblico l’allontanamento dalla traiettoria
più prevedibile.
fig.7- Passo di danza Grand Jeté; fig.8 - Posizione della testa della ballerina nel tempo durante il passo Grand Jeté
Il trucco è compiere durante il salto una spaccata in aria sollevando al tempo stesso le
braccia, il successivo spostamento verso il basso degli arti comporta, anche senza lo
spostamento del capo, un abbassamento del centro di massa.
Se l’insieme dei punti materiali è costituito solo da due masse m 1 e m2 interagenti con
forze apposte F1=-F2 con interazioni trascurabili con l’esterno, il sistema è isolato. Per
il sistema l’accelerazione del centro di massa è nulla. Un riferimento cartesiano
vincolato al centro di massa è allora inerziale. Il centro di massa rispetto un
riferimento esterno è fermo o in moto rettilineo uniforme.
Il vettore: rcm= (m1r1 + m2r2)/(m1+ m2)
e la quantità di moto totale: pcm= m1v1 + m2v2 = Mvcm
rimangono costanti. Inoltre poiché in ogni istante r2 – r1 è parallelo alle forze, ne
consegue che il momento della coppia di forze è uguale a zero. Ne deriva che anche il
momento angolare:
Lcm= r1 x p1+ r2 x p2 = rcm x pcm si conserva.
Il momento d’inerzia
Il sistema di due sferette con un’ideale asta (massa trascurabile) che le unisce può
essere pensato come un semplice corpo rigido. Se il manubrio in figura 9 viene fatto
ruotare intorno all’asse perpendicolare al piano e passante per il centro di massa da
una coppia di forze esterne le due masse percorrono le circonferenze di raggi r 1 e r2 (il
riferimento è il centro di massa e quindi m 1r1=m2r2). Supponendo che i moti piani
siano circolari uniformi, è facile dimostrare che: v 1/r1=v2/r2. Questi rapporti
definiscono il modulo della velocità angolare ovvero della variazione dell’angolo
nell’unità di tempo. A parità di tempo la massa m1 percorre un tratto minore di m2,
ma entrambe le masse hanno subito lo stesso “spostamento” angolare α (l’asta è
indeformabile). Nelle rotazioni rispetto un asse fisso che individua la direzione del
vettore velocità angolare, è più importante l’angolo della distanza, la velocità angolare
rispetto a quella tangenziale. Prendiamo adesso in esame l’energia cinetica K del
sistema.
fig.9 - Rotazione di due masse diverse intorno al centro di massa; fig.10 - Momento d’inerzia rispetto un asse di un insieme di
masse puntiformi
Per la proprietà additiva della grandezza, si può scrivere:
K= m1v12/2 + m2v22/2.
L’espressione precedente può essere trasformata con l’intensità della velocità angolare
ω, in:
K= (m1r12 + m2r22) ω2/2.
Rispetto alla situazione con un’unica massa, l’energia cinetica K è sempre la
semisomma di una velocità al quadrato per l’inerzia solo che il termine m è sostituito
da m1r12 + m2r22. La nuova grandezza caratteristica delle rotazioni è il momento
d’inerzia I e permette di riscrivere l’espressione dell’energia cinetica complessiva come
I ω2/2.
Il termine inerzia rimanda a un’altra analogia: come nella traslazione la massa
contrasta i cambiamenti dello stato di moto dovuto alle forze (a parità di forza, massa
e accelerazione sono inversamente proporzionali), così nelle rotazioni di un corpo
rigido, il momento d’inerzia tende a limitare le variazioni della velocità angolare. Nel
senso che tanto è più grande I, tanto più difficile è modificare la velocità angolare. Se
invece di due masse si ha un insieme n di punti materiali, il calcolo del momento
d’inerzia rispetto un asse arbitrario si può generalizzare secondo la sommatoria
I = Σ mi ri2,
dove ri sono le distanze dei punti dall’asse. In un moto piano l’asse naturale di
riferimento è quello passante per il centro di massa e perpendicolare al piano.
Quando invece il corpo è solido e la rotazione avviene intorno a una retta orientata
nello spazio è assai difficile darne una descrizione semplice. Innanzitutto il calcolo dei
momenti d’inerzia implica il passaggio dal discreto al continuo, in secondo luogo vanno
utilizzati più momenti d’inerzia. Si può mostrare che tutti i solidi hanno tre assi, aventi
come punto comune il centro di massa, con proprietà particolari. La rotazione rispetto
a un asse principale d’inerzia, solidale al corpo, comporta una relazione semplice tra il
momento angolare e la velocità angolare:
L = Iω.
I due vettori hanno la stessa direzione e lo stesso verso. Inoltre l’equazione
precedente può essere vista come l’analoga per le traslazioni della quantità di moto:
p = mv.
Per una figura semplice come il cilindro di raggio r e lunghezza l, gli assi principali
d’inerzia sono: l’asse longitudinale passante per i centri delle circonferenze e una
coppia di assi perpendicolari trasversali passanti per il centro di massa. Il calcolo del
momento d’inerzia per l’asse longitudinale dipenderà da mr 2, mentre per gli altri due
momenti da ml2 (oltre che da mr2). Indicando con I1, I2, I3 i momenti d’inerzia
calcolati rispetto ai tre assi principali, per questioni di simmetria I 2=I3. Inoltre è facile
capire che I2 supererà I1 non appena la lunghezza sarà sufficientemente più grande
del raggio (i due momenti d’inerzia sono uguali per l = r√3 ≅1,73 r). Per concludere,
l’energia cinetica di un corpo rigido è:
K= I1ω12/2 + I2ω22/2 + I3ω32/2.
fig.11 - Momenti d’inerzia di un cilindro rispetto agli assi principali
Salti mortali e avvitamenti
Negli sport acrobatici (pattinaggio artistico, tuffi) nell’atletica (salto in alto), nella
ginnastica artistica, il controllo del corpo in un salto permette la realizzazione di
complesse figure di rotazione, studiate solo in tempi relativamente recenti.
Trascurando gli effetti della resistenza dell’aria, quando l’atleta è “in volo” il momento
delle forze esterne è uguale a zero quindi deve valere il principio di conservazione del
momento angolare. Per capire come sia possibile modificare un salto mortale con una
figura con avvitamento o addirittura realizzare una rotazione a partire da un momento
angolare iniziale nullo, bisogna prima parlare degli assi principali d’inerzia del corpo
umano. Considerando una figura eretta, in analogia al discorso precedente sul cilindro,
si possono idealmente tracciare dei segmenti, solidali al corpo, che si intersecano nel
centro di massa: l’asse longitudinale, quello trasversale e l’asse frontale.
fig.12 - Piani di simmetria e assi di rotazione per il corpo umano
Semplificheremo il nostro discorso tralasciando le rotazioni intorno all’asse frontale. Le
figure base degli esercizi acrobatici sono: il salto mortale (in inglese somersault) e
l’avvitamento (twist). Il primo è una rotazione testa-piedi intorno all’asse trasversale
passante attraverso il bacino e i fianchi. L’avvitamento è una rotazione secondo l’asse
longitudinale che attraversa la testa e i piedi. Per una trattazione completa
bisognerebbe come abbiamo già accennato considerare un terzo angolo che in inglese
è chiamato tilt.
fig.13 - Schematizzazione di un ginnasta che esegue un salto mortale all’indietro; fig.14 - Atleta durante
una rotazione rispetto al suo asse longitudinale verticale
Il punto chiave è che i momenti d’inerzia del corpo umano, come quelli del cilindro, I 1
rispetto all’asse longitudinale e I2 rispetto all’asse trasversale, sono diversi. Le masse
del corpo per una postura eretta sono molto più vicine all’asse longitudinale che non a
quello trasversale (i punti più distanti nel primo caso raramente superano i trenta
centimetri mentre nel secondo caso spesso raggiungono i novanta centimetri). In un
semplice salto mortale avremo allora:
L1 = I1ω1.
In un avvitamento puro:
L2 = I2ω2.
Combinando i due esercizi il momento angolare complessivo, per la proprietà di
additività, è:
L = L1+ L2 = I1ω1 + I2ω2.
D’altra parte anche le due velocità angolari si sommano vettorialmente per dare la
velocità angolare complessiva:
ω = ω 1+ ω 2.
fig.15 - Composizione delle velocità angolari in un salto mortale con avvitamento
Dalle equazioni precedenti è evidente che i vettori caratteristici delle rotazioni (il
momento angolare totale L e la somma delle velocità angolari ω) non hanno la stessa
direzione poiché I1 ≠ I2. In altre parole l’asse di rotazione caratteristico della velocità
angolare è diverso da quello che individua il momento angolare e non vale più la
relazione caratteristica degli assi principali d‘inerzia: L=I ω.
Un altro aspetto ancora da chiarire è che l’atleta ha la possibilità di variare i propri
momenti d’inerzia ad esempio avvicinando le braccia e le gambe agli assi.
Ora abbiamo tutti gli elementi per applicare il principio di conservazione del momento
angolare a un esercizio acrobatico. Un tuffatore che inizia un salto mortale grazie al
contatto con la piattaforma, può, grazie a una disposizione delle braccia asimmetriche,
iniziare in aria un avvitamento. La riduzione del momento d’inerzia dell’asse
trasversale determina una diminuzione del momento angolare del salto mortale,
tuttavia questa è compensata dalla componente di avvitamento in modo tale che il
momento angolare complessivo rimanga costante. In ogni istante deve valere:
L1+ L2 = I1ω1 + I2ω2 = costante;
ma ciò non significa che variando i momenti d’inerzia, attraverso movimenti complessi
del corpo, non si possano modificare le grandezze angolari.
fig.16 -Tuffo con salto mortale e mezzo in avanti con triplo
avvitamento
Non solo durante un salto è possibile
realizzare rotazioni anche con un
momento angolare iniziale uguale a
zero. Per capire questo aspetto è più
facile affidarsi all’atleta per eccellenza in
questa specialità: il gatto.
La sua capacità di atterrare sempre sulle quattro zampe in una caduta
verso terra è stata studiata ripetutamente con sistemi di riprese di filmati
al rallentatore (slow motion) e, dagli anni Sessanta, è stata modellizzata
con sistemi meccanici. Il paradosso è la violazione (apparente) del
principio di conservazione del momento angolare. Anche con L=0 (gatto a
testa in giù, lasciato cadere) il felino inizia a compiere le sue miracolose
rotazioni. Nei fotogrammi di figura 17 sono illustrate alcune fasi
dell’acrobazia. I movimenti istintivi in aria del gatto suddividono il suo
corpo in due zone con diversi momenti d’inerzia, diciamo uno grande e
uno piccolo. Le due parti sono poi ruotate in versi opposti. Il momento
angolare totale deve rimanere uguale a zero visto l’intervento di sole
forze interne, ciò non esclude una rotazione netta del corpo.
Inizialmente la parte anteriore (con minore momento d’inerzia) ruota
più velocemente di quella posteriore “percorrendo” quasi 180°, mentre
quella posteriore è ruotata solo di pochi gradi. Modificando di nuovo i
momenti d’inerzia (tendendo le zampe anteriori e ritraendo quelle
posteriori) le velocità di rotazione si invertono completando l’assetto
verticale, la coda permette piccole variazioni. Un esempio sportivo è
quello di un esercizio, delle ginnaste nelle parallele asimmetriche, dove
la rotazione di 180° netta avviene in aria dopo aver abbandonato la
sbarra. Inizialmente l’atleta fa una spaccata con il bacino
apparentemente fermo e ruota la parte superiore del corpo. Dopo,
grazie ai movimenti delle braccia mirati a invertire i momenti d’inerzia
delle due parti del corpo, ruota le gambe. Molti atleti utilizzano
tecniche simili per compiere mirabolanti acrobazie, ma non possono
certo eguagliare il re della rotazione che ha dalla sua un innato senso
della posizione e una particolare struttura ossea.
fig.17 - Sequenza fotografica della caduta di un gatto;
fig.18 - Esercizio di rotazione di 180° di una ginnasta effettuato in aria












