Analisi grafico spazio – tempo (s-t)

Analisi grafico spazio – tempo (s-t)
Si prende in considerazione il moto di un corpo che si muove lungo una retta. Per analizzare
tale moto si hanno a disposizione degli strumenti che misurano la posizione (un righello graduato)
del corpo rispetto ad un osservatore, O, e l’istante di tempo (un cronometro) in cui si trova il corpo.
La posizione e l’istante di tempo costituiscono un evento. L’osservatore esegue una raccolta di dati,
cioè misura la posizione del corpo ad un certo istante di tempo. Tali dati vengono raccolti in una
tabella e successivamente riportati su di un sistema di assi cartesiani per l’analisi del moto, e quindi
poter scrivere, se possibile, le equazioni orarie del moto.
Le equazioni del moto, in genere, sono due:
1)
la prima si riferisce alla posizione del corpo, cioè permette di conoscere la posizione
del corpo ad un certo istante di tempo.
Esempio: Il moto di un corpo è descritta da una equazione del tipo:
s = 2t2 – 5t +3
dove
t, che è la variabile indipendente, indica l’istante di tempo;
s, che è la variabile dipendente, indica la posizione del corpo ad un certo istante di
tempo.
Si vuole conoscere la posizione del corpo all’istante di tempo
t = 3s
Per conoscere la posizione del corpo basta sostituire nell’equazione alla variabile t il
valore assegnato (t = 3s):
s = 2(3)2 - 5(3) + 3
s = 29 – 15 + 3 = 18 – 15 +3
s=6m
Quindi il corpo all’istante t = 3s si trova a 6m dall’osservatore.
Quando si analizza il moto, poiché il corpo si muove lungo una retta, è necessario
specificare se si trova a destra dell’osservatore oppure a sinistra. Per convenzione,
se si trova a destra, la posizione sarà un numero positivo, invece, se si trova a
sinistra la posizione sarà un numero negativo.
2)
la seconda equazione si riferisce alla velocità con cui si muove il corpo ad un certo
istante di tempo. Cioè l’equazione permette di calcolare la velocità ad un certo istante
di tempo.
Esempio: Il moto di un corpo è descritta dalla seguente equazione:
v = 4t +9
dove:
t è il tempo, ovvero la variabile indipendente;
v è la velocità che il corpo ad un certo istante di tempo;
9 è la velocità del corpo all’istante zero.
Applicazione della equazione del moto: Si vuole conoscere la velocità del corpo
all’istante:
t = 5s
Per trovare il valore della velocità, si sostituisce il valore del tempo nell’equazione
del moto:
v = 4(5) + 9
v = 20 + 9
v = 29
1
In conclusione, all’istante t = 5s, il corpo si muove con una velocità istantanea pari a
v  29
m
s
I moti che si studiano sono:
a) Moto rettilineo uniforme (MRU) in cui il corpo si muove lungo una retta con velocità
costante. Le equazioni del moto sono:
v = costante
s = vt + s0
dove:
v è la velocità costante con cui si muove il corpo;
t è il tempo;
s0 è la posizione che ha il corpo all’istante zero (t = 0s).
s è la posizione del corpo ad un certo istante.
Esempio di equazione del MRU:
v  4m  s 1
s  4t  7
Dall’equazione si deduce che il corpo si muove a velocità costante (v=4ms-1) e che all’istante
iniziale (t=0s) il coro si trova a 7m dall’osservatore:
b) Moto rettilineo uniformemente accelerato (MRUA) oppure moto rettilineo uniformemente
vario (MRUV), cioè il corpo varia la sua velocità costantemente.
Le equazioni del moto del corpo sono:
v  a  t  v0
s
1
 a  t 2  v0  t  s0
2
dove:
a è l’accelerazione del corpo;
v0 è la velocità del corpo all’istante iniziale (t=0s);
s0 è la posizione del corpo all’istante iniziale (t=0s);
t è il tempo;
v è la velocità ad un certo istante;
s è la posizione ad un certo istante.
Esempio: L’equazione del moto relativa alla velocità è:
v  3t  6
Il corpo si muove con una accelerazione pari a:
a  3m  s 2
E all’istante iniziale (t=0s) ha una velocità pari a:
v  6m  s 1
2
L’equazione del moto relativa alla posizione è :
s
1
 3t2  6t  8
2
Il corpo si muove con accelerazione:
a  3ms 2
La velocità all’istante iniziale vale
v  6m  s 1
La posizione all’istante iniziale è:
s = 8m
Oltre che matematicamente, il moto di un corpo può essere decritto da un grafico in cui sono
riportati i dati sperimentali raccolti durante l’esperimento, cioè il tempo, le posizioni e le velocità.
Grafici possono essere di due tipi: posizione-tempo (s-t) e velocità-tempo (v-t). Nel primo
caso, su di un sistema di assi cartesiani si posiziona sull’asse delle ascisse il tempo, mentre sull’asse
delle ordinate la posizione del corpo. Nel secondo caso, sull’asse delle ascisse si posiziona ancora il
tempo, mentre sull’asse delle ordinate si posiziona la velocità.
Adesso, mediate un esempio, si analizzeranno due grafici e si mostrerà come tirar fuori delle
informazioni circa il moto dell’oggetto.
Analisi grafico spazio -tempo
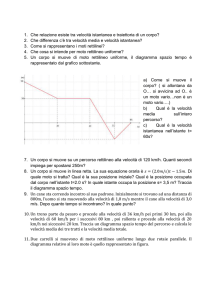
Si consideri il seguente grafico spazio – tempo di un moto rettilineo di un corpo.
Ogni punto del piano viene chiamato evento, dove per evento si intende qualcosa che accade
in un certo posto ad un certo istante di tempo. Ogni evento è individuato da due coordinate: la prima
indica l’istante di tempo, la seconda la posizione.
Nel grafico gli eventi di riferimento sono indicati dai punti A, B, C, D, E, F e G. Le
coordinate di tali eventi sono:
A0s, 2m ;
C5s, 2m ;
B3s, 3m;
3
D9s, 6m
E11s, 2m ;
F15s,  1m ;
G16s, 3m
Analisi del grafico:
1)
Tra gli eventi A e B, il corpo si muove a velocità costante; ciò deriva dal fatto che la
linea che congiunge i due unti è un tratto di retta, il cui coefficiente angolare non è
altro che la velocità con cui si muove il corpo nell’intervallo di tempo tA=0s e tB=3s.
Il valore della velocità, vAB, si calcola applicando la sua definizione:
s s B  s A 3m  2m 1m
v AB 



 0,33m  s 1
3s  0s 3s
t t B  t A
Equazione del moto
Poiché il corpo si muove a velocità costante, l’equazione del moto ha la stessa
struttura dell’equazione di una retta, dove il coefficiente angolare è la velocità.
Quindi l’equazione del moto rettilineo uniforme è:
s  v  t  s0
Dove:
v è la velocità con cui si muove il corpo. Nel caso in esame si ha:
v = vAB  0,33 ms-1,
s0 è la posizione del corpo all’istante t=0s. Nel caso in esame il corpo all’istante
t=0s si trova a 2 m dall’osservatore pertanto:
s0 = 2m
Sostituendo i valori si ottiene l’equazione del moto tra gli eventi A e B.
s  0,33  t  2
Questa equazione permette di calcolare la posizione del corpo nell’intervallo di
tempo compreso tra 0s e 3s.
2)
3)
Tra gli eventi B e C il corpo, al trascorrere del tempo, si trova sempre nella stessa
posizione, ciò significa che il corpo è fermo, e la velocità è nulla.
Tra gli eventi C e D, il corpo continua ad allontanarsi dall’osservatore a velocità
costante (situazione simile a ciò che avviene tra gli eventi A e B). il valore della
velocità, vCD, è:
s s D  s C 6m  3m 3m
v CD 



 0,75m  s 1
9s  5s 4s
t t D  t C
L’equazione del moto, tra gli eventi C e D, è:
s  v  t  s0
dove i simboli hanno lo stesso significato di quanto detto nel punto 1).
v = vCD = 0,75ms-1;
La posizione iniziale, s0, non è possibile rilevarla dal grafico, se non in maniera
approssimata. Il valore della posizione iniziale si calcola nel seguente modo:
Nell’equazione del moto s e t sono le variabili mentre v ed s0 sono le costanti. Le
variabili s e t sono le coordinate degli infiniti punti della retta che passa per i punti C
e D. Degli infiniti punti di cui è costituita la retta, si conoscono le coordinate di due
di essi, cioè i punti C e D. Si considera uno dei due punti, ad esempio il punto C, e si
sostituiscono le sue coordinate nell’equazione del moto:
Le coordinate del punto C sono:
C5s, 2m
4
Sostituendo tali valori nell’equazione del moto si ha:
2  0,75  5  s0
2  3,75  s0
2  3,75  s 0
s 0  1,75
Il significato del risultato ottenuto, s0=-1,75m, è il seguente: se il corpo si fosse
mosso sempre alla stessa velocità di 0,75 ms-1 si troverebbe, all’istante iniziale t=0s,
ad 1,75m prima dell’osservatore. Le posizione del corpo prima del’osservatore
sono indicate da valori negativi, mentre le posizioni del corpo dopo l’osservatore da
numeri positivi.
In conclusione, l’equazione del moto è:
s  0,75  t  1,75
4)
Tra gli eventi D ed E il corpo continua a muoversi di moto rettilineo uniforme, però il
corpo ritorna indietro verso l’osservatore. Infatti all’istante t=9s il corpo si trova a 6m
dall’osservatore, mentre successivamente, all’istante t=11s, il corpo si trova a 2m
dall’osservatore.
Il calcolo della velocità e dell’equazione del moto è identico a quello del caso
precedente.
La velocità tra gli eventi D ed E è:
v DE 
s s E  s D 2m  6m  4m



 2m  s 1
11s  9s 2s
t t E  t D
Il valore della velocità è negativo, ciò significa che il corpo sta tornando indietro.
Per il calcolo dell’equazione del moto, si prende in considerazione uno dei due
eventi D ed E, ad esempio l’evento:
D(9s, 6m)
Sostituendo i valori nell’equazione del moto:
s  v  t  s0
si ha:
6   2 9  s0
Elaborando, si ottiene s0, che è la posizione iniziale, t=0s, che avrebbe il corpo se si
muovesse sempre alla stessa velocità.
6   2 9  s0
6  18  s0
s 0  24
Quindi l’equazione del moto, tra gli eventi D ed E, è:
s  2  t  24
5
5)
Tra gli eventi E ed F, il corpo si muove di moto uniforme e continua ad avvicinarsi
all’osservato, anzi, prima di t=14s, il corpo oltrepassa l’osservatore.
Il calcolo dei parametri che compongono l’equazione del moto è identico a ciò che è
stato fatto in precedenza.
La velocità vale:
v EF 
s s F  s E  1m  2m  3m



 1m  s 1
15s  11s
t t F  t E
3s
Prendo come evento di riferimento il punto E, il calcolo dell’equazione del moto è il
seguente:
s  v  t  s0
2  1  11  s0
2  1  11  s 0
2  22  s0
s 0  24
In conclusione, l’equazione del moto è:
s  1  t  24
6)
Tra gli eventi F e G, il corpo si muove di moto uniforme ed inverte il moto, ovvero,
riprende a muoversi in avanti.
La velocità è:
v FG 
s s G  s F 3m   1m  4m



 4m  s 1
16s  15s 1s
t t G  t F
La velocità ridiventa positiva.
Prendendo come evento di riferimento il punto F, il calcolo dell’equazione del moto
diventa:
s  v  t  s0
 1  4  15  s 0
 1  4  15  s0
 1  60  s0
s 0  61m
In conclusione, l’equazione del moto è:
s  4  t  61
6